2021-2022学年人教版数学九年级上册 24.4弧长和扇形面积同步习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册 24.4弧长和扇形面积同步习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 526.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 18:30:51 | ||
图片预览



文档简介
2021-2022学年初中数学九年级上册(人教版)
24.4弧长和扇形面积-同步习题
时间:40分钟
一、单选题
1.已知某扇形的半径为6,圆心角的度数为,则扇形的弧长为( )
A. B. C. D.
2.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是( )
A.90° B.120° C.180° D.135°
3.在圆心角为的扇形中,半径,则扇形的面积是( )
A. B. C. D.
4.一个商标图案如图中阴影部分,在长方形中,,,以点为圆心,为半径作圆与的延长线相交于点,则商标图案的面积是( )
A. B.
C. D.
5.如图,在Rt中,∠BCA=90° 两分圆别以为半径画圆,则阴影部分的面积为( )
A. B. C. D.
6.将某圆锥形的冰淇淋纸套沿它的一条母线展开 若不考虑接缝,它是一个半径为12cm,圆心角为的扇形,则
A.圆锥形冰淇淋纸套的底面半径为8cm B.圆锥形冰淇淋纸套的底面半径为6cm
C.圆锥形冰淇淋纸套的高为 D.圆锥形冰淇淋纸套的高为
二、填空题
7.75°的圆心角所对的弧长是2.5cm,则此弧所在圆的半径是_____cm.
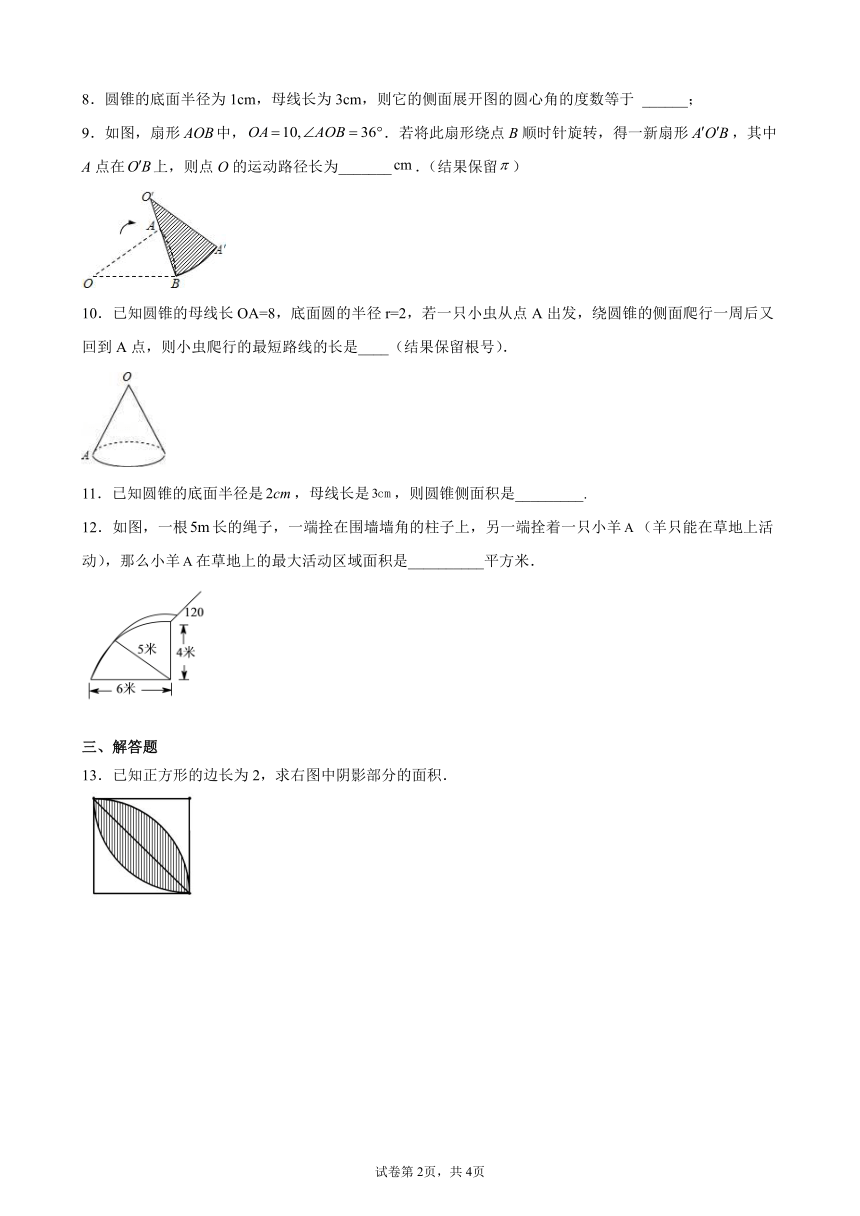
8.圆锥的底面半径为1cm,母线长为3cm,则它的侧面展开图的圆心角的度数等于 ______;
9.如图,扇形中,.若将此扇形绕点B顺时针旋转,得一新扇形,其中A点在上,则点O的运动路径长为_______.(结果保留)
10.已知圆锥的母线长OA=8,底面圆的半径r=2,若一只小虫从点A出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是____(结果保留根号).
11.已知圆锥的底面半径是,母线长是,则圆锥侧面积是_________.
12.如图,一根长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊(羊只能在草地上活动),那么小羊在草地上的最大活动区域面积是__________平方米.
三、解答题
13.已知正方形的边长为2,求右图中阴影部分的面积.
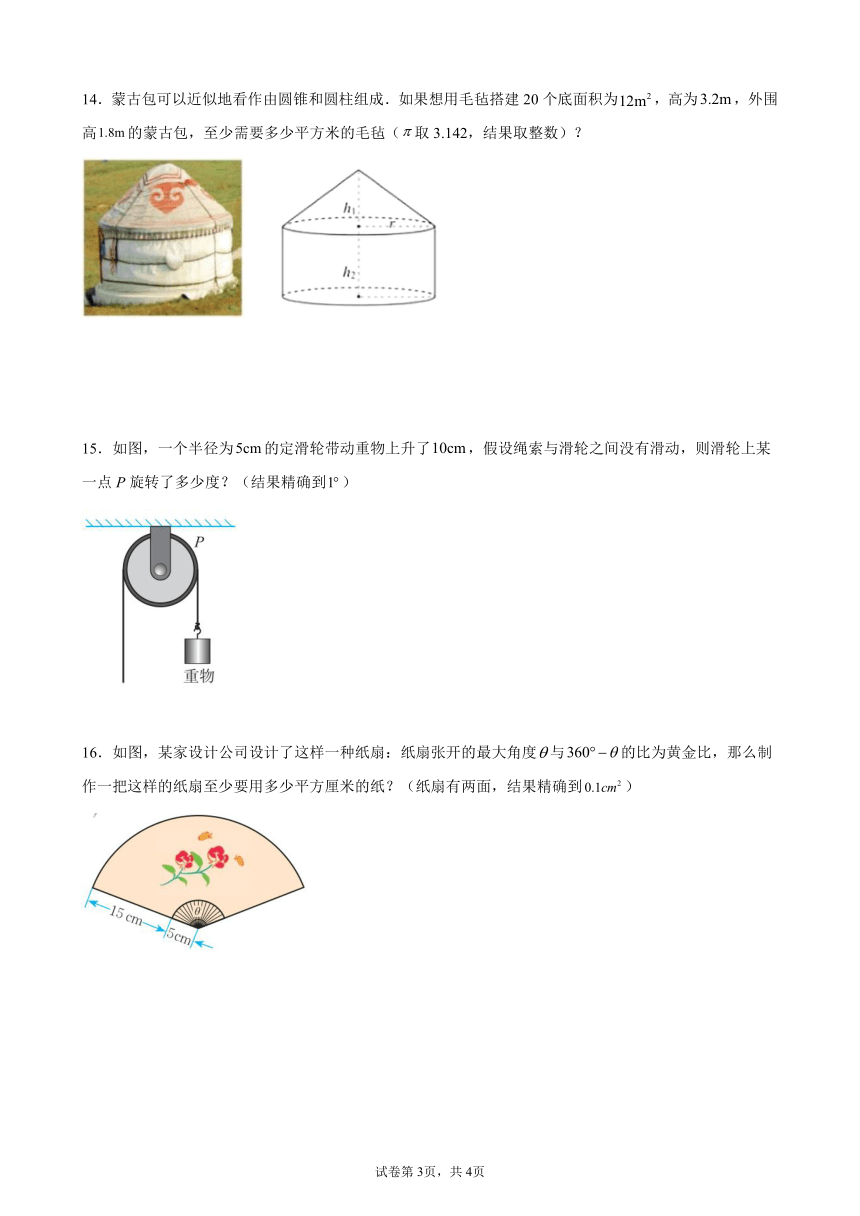
14.蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20个底面积为,高为,外围高的蒙古包,至少需要多少平方米的毛毡(取3.142,结果取整数)?
15.如图,一个半径为的定滑轮带动重物上升了,假设绳索与滑轮之间没有滑动,则滑轮上某一点P旋转了多少度?(结果精确到)
16.如图,某家设计公司设计了这样一种纸扇:纸扇张开的最大角度与的比为黄金比,那么制作一把这样的纸扇至少要用多少平方厘米的纸?(纸扇有两面,结果精确到)
17.已知扇形的圆心角为120°,面积为300πcm2.
(1)求扇形的弧长;
(2)若把此扇形卷成一个圆锥,则这个圆锥的轴截面面积是多少?
18.如图,圆锥母线的长l等于底面半径r的4倍,
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【解析】∵扇形的半径为6,圆心角的度数为,
∴.
故选C.
2.C
【解析】解:由题意得,2π=,
解得:n=180.
即这条弧所对的圆心角的度数是180°.
故选C.
3.C
【解析】解:由题意得扇形的面积是.
故选C.
4.D
【解析】解:作辅助线DE、EF使BCEF为一矩形.
则S△CEF=(8+4)×4÷2=24cm2,
S正方形ADEF=4×4=16cm2,
S扇形ADF==4πcm2,
∴阴影部分的面积=24-(16-4π)=.
故选:D.
5.A
【解析】设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分
面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=π-4.
故选A.
6.C
【解析】解:解:半径为12cm,圆心角为120°的扇形弧长是:(cm)
设圆锥的底面半径是r(cm)
则:2πr=8π,解得:r=4
即个圆淋的底面半径是4cm;
圆锥形冰淇淋纸套的高为(cm).
故答案为C.
7.6
【解析】解:由题意得:圆的半径.
故本题答案为:6.
8.120°
【解析】设圆心角为n,底面半径是1,
则底面周长
∴
故答案为:
9.4π.
【解析】解:根据题意,知OA=OB.
又∠AOB=36°,
∴∠OBA=72°.
∴点O旋转至O′点所经过的轨迹长度==4πcm.
故答案是:4π.
10.8
【解析】圆锥的侧面展开图,如图所示:∵圆锥的底面周长=2π×2=4π,
设侧面展开图的圆心角的度数为n.∴=4π,解得n=90,
∴最短路程为: =8.
故答案为8.
11.
【解析】根据圆锥的侧面积公式:
底面半径是2cm,母线长是3cm的圆锥侧面积为
故答案是:
12..
【解析】解:如图.小羊的活动范围是:(平方米)
故答案为.
13.2.28
【解析】解:根据题意,则
.
14.
【解析】解:如图是一个蒙古包的示意图.
根据题意,下部圆柱的底面积为,高;上部圆锥的高.
圆柱的底面圆的半径,
侧面积为.
圆锥的母线长,
侧面展开扇形的弧长为,
圆锥的侧面积为.
因此,搭建20个这样的蒙古包至少需要毛毡.
15.旋转了约
【解析】解:∵半径为5cm,重物上升了10cm,
根据,
解得n≈115°.
答:滑轮上某一点P旋转了约.
16.约
【解析】解:∵θ与360°-θ的比为黄金比,
∴
解得:
∴所用纸的面积=cm2
17.(1)扇形的弧长是20πcm;(2)卷成圆锥的轴截面是200cm2.
【解析】(1)∵300π=,
∴R=30,
∴弧长L=20π(cm);
(2)如图所示:
∵20π=2πr,
∴r=10,R=30,
AD=,
∴S轴截面=×BC×AD=×2×10×20=200cm2.
答:扇形的弧长是20πcm卷成圆锥的轴截面是200cm2.
18.(1)它的侧面展开图的圆心角为90°;(2)BB′=8.
【解析】解:(1)设它的侧面展开图的圆心角为n°,
根据题意得2πr=,
而l=2r,
所以2πr=,解得n=90,
所以它的侧面展开图的圆心角为90°;
(2)连接BB′,如图,
此时BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,
∵r=4,
∴l=2r=8,
∵∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴BB′=AB=8.
答案第1页,共2页
答案第1页,共2页
24.4弧长和扇形面积-同步习题
时间:40分钟
一、单选题
1.已知某扇形的半径为6,圆心角的度数为,则扇形的弧长为( )
A. B. C. D.
2.有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是( )
A.90° B.120° C.180° D.135°
3.在圆心角为的扇形中,半径,则扇形的面积是( )
A. B. C. D.
4.一个商标图案如图中阴影部分,在长方形中,,,以点为圆心,为半径作圆与的延长线相交于点,则商标图案的面积是( )
A. B.
C. D.
5.如图,在Rt中,∠BCA=90° 两分圆别以为半径画圆,则阴影部分的面积为( )
A. B. C. D.
6.将某圆锥形的冰淇淋纸套沿它的一条母线展开 若不考虑接缝,它是一个半径为12cm,圆心角为的扇形,则
A.圆锥形冰淇淋纸套的底面半径为8cm B.圆锥形冰淇淋纸套的底面半径为6cm
C.圆锥形冰淇淋纸套的高为 D.圆锥形冰淇淋纸套的高为
二、填空题
7.75°的圆心角所对的弧长是2.5cm,则此弧所在圆的半径是_____cm.
8.圆锥的底面半径为1cm,母线长为3cm,则它的侧面展开图的圆心角的度数等于 ______;
9.如图,扇形中,.若将此扇形绕点B顺时针旋转,得一新扇形,其中A点在上,则点O的运动路径长为_______.(结果保留)
10.已知圆锥的母线长OA=8,底面圆的半径r=2,若一只小虫从点A出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是____(结果保留根号).
11.已知圆锥的底面半径是,母线长是,则圆锥侧面积是_________.
12.如图,一根长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊(羊只能在草地上活动),那么小羊在草地上的最大活动区域面积是__________平方米.
三、解答题
13.已知正方形的边长为2,求右图中阴影部分的面积.
14.蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20个底面积为,高为,外围高的蒙古包,至少需要多少平方米的毛毡(取3.142,结果取整数)?
15.如图,一个半径为的定滑轮带动重物上升了,假设绳索与滑轮之间没有滑动,则滑轮上某一点P旋转了多少度?(结果精确到)
16.如图,某家设计公司设计了这样一种纸扇:纸扇张开的最大角度与的比为黄金比,那么制作一把这样的纸扇至少要用多少平方厘米的纸?(纸扇有两面,结果精确到)
17.已知扇形的圆心角为120°,面积为300πcm2.
(1)求扇形的弧长;
(2)若把此扇形卷成一个圆锥,则这个圆锥的轴截面面积是多少?
18.如图,圆锥母线的长l等于底面半径r的4倍,
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
【解析】∵扇形的半径为6,圆心角的度数为,
∴.
故选C.
2.C
【解析】解:由题意得,2π=,
解得:n=180.
即这条弧所对的圆心角的度数是180°.
故选C.
3.C
【解析】解:由题意得扇形的面积是.
故选C.
4.D
【解析】解:作辅助线DE、EF使BCEF为一矩形.
则S△CEF=(8+4)×4÷2=24cm2,
S正方形ADEF=4×4=16cm2,
S扇形ADF==4πcm2,
∴阴影部分的面积=24-(16-4π)=.
故选:D.
5.A
【解析】设各个部分的面积为:S1、S2、S3、S4、S5,如图所示,
∵两个半圆的面积和是:S1+S5+S4+S2+S3+S4,△ABC的面积是S3+S4+S5,阴影部分
面积是:S1+S2+S4,
∴图中阴影部分的面积为两个半圆的面积减去三角形的面积.
即阴影部分的面积=π×4+π×1-4×2÷2=π-4.
故选A.
6.C
【解析】解:解:半径为12cm,圆心角为120°的扇形弧长是:(cm)
设圆锥的底面半径是r(cm)
则:2πr=8π,解得:r=4
即个圆淋的底面半径是4cm;
圆锥形冰淇淋纸套的高为(cm).
故答案为C.
7.6
【解析】解:由题意得:圆的半径.
故本题答案为:6.
8.120°
【解析】设圆心角为n,底面半径是1,
则底面周长
∴
故答案为:
9.4π.
【解析】解:根据题意,知OA=OB.
又∠AOB=36°,
∴∠OBA=72°.
∴点O旋转至O′点所经过的轨迹长度==4πcm.
故答案是:4π.
10.8
【解析】圆锥的侧面展开图,如图所示:∵圆锥的底面周长=2π×2=4π,
设侧面展开图的圆心角的度数为n.∴=4π,解得n=90,
∴最短路程为: =8.
故答案为8.
11.
【解析】根据圆锥的侧面积公式:
底面半径是2cm,母线长是3cm的圆锥侧面积为
故答案是:
12..
【解析】解:如图.小羊的活动范围是:(平方米)
故答案为.
13.2.28
【解析】解:根据题意,则
.
14.
【解析】解:如图是一个蒙古包的示意图.
根据题意,下部圆柱的底面积为,高;上部圆锥的高.
圆柱的底面圆的半径,
侧面积为.
圆锥的母线长,
侧面展开扇形的弧长为,
圆锥的侧面积为.
因此,搭建20个这样的蒙古包至少需要毛毡.
15.旋转了约
【解析】解:∵半径为5cm,重物上升了10cm,
根据,
解得n≈115°.
答:滑轮上某一点P旋转了约.
16.约
【解析】解:∵θ与360°-θ的比为黄金比,
∴
解得:
∴所用纸的面积=cm2
17.(1)扇形的弧长是20πcm;(2)卷成圆锥的轴截面是200cm2.
【解析】(1)∵300π=,
∴R=30,
∴弧长L=20π(cm);
(2)如图所示:
∵20π=2πr,
∴r=10,R=30,
AD=,
∴S轴截面=×BC×AD=×2×10×20=200cm2.
答:扇形的弧长是20πcm卷成圆锥的轴截面是200cm2.
18.(1)它的侧面展开图的圆心角为90°;(2)BB′=8.
【解析】解:(1)设它的侧面展开图的圆心角为n°,
根据题意得2πr=,
而l=2r,
所以2πr=,解得n=90,
所以它的侧面展开图的圆心角为90°;
(2)连接BB′,如图,
此时BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,
∵r=4,
∴l=2r=8,
∵∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴BB′=AB=8.
答案第1页,共2页
答案第1页,共2页
同课章节目录
