2021-2022学年北师大版数学九年级上册第四章 图形的相似 章节测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级上册第四章 图形的相似 章节测试(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 592.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 18:55:27 | ||
图片预览



文档简介
图形的相似
一、单选题
1.如图,点G、F分别是的边、上的点,的延长线与的延长线相交于点A,交于点E,则下列结论错误的是( )
A. B. C. D.
2.如图,点P是△ABC的边AC上一点,连结BP,以下条件中,不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
3.甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
4.已知如图,点 C 是线段 AB 的黄金分割点(AC>BC),则下列结论中正确的是( )
A.AB2=AC2+BC2 B.BC2=AC BA
C. D.
5.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12.在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE的长为( )
A.16 B.14 C.16或14 D.16或9
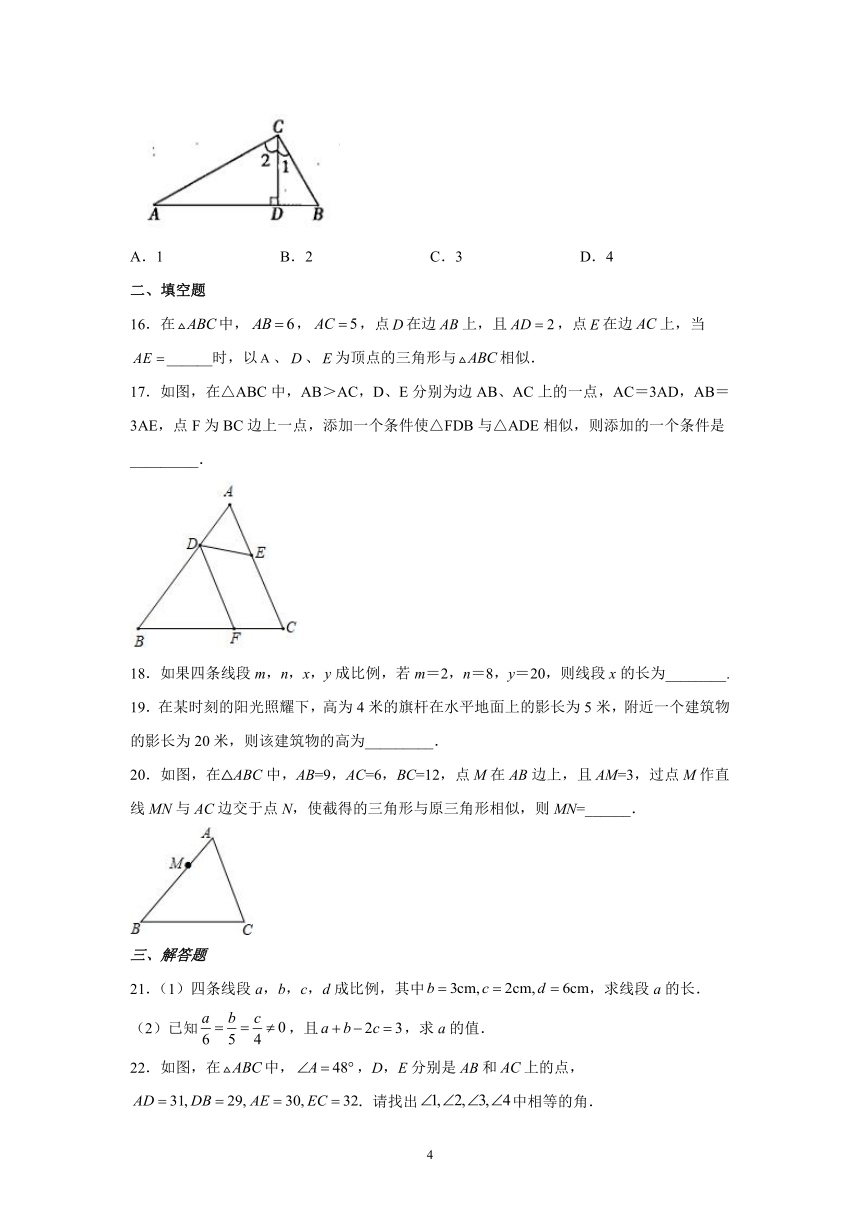
6.如图,中,于D,下列条件,①;②;③;④.其中一定能够判定是直角三角形的有( )种.
A.4 B.3 C.2 D.1
7.已知△ABC∽△DEF,相似比为3:1,且△ABC的周长为18,则△DEF的周长为( )
A.2 B.3 C.6 D.54
8.将直角三角形三边扩大同样的倍数,得到的新三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.任意三角形
9.下列比例式中,不能由得到的比例式是
A. B. C. D.
10.若的每条边长增加各自的得,则的度数与其对应角的度数相比( )
A.增加了 B.减少了 C.增加了 D.没有改变
11.如图,平行四边形ABCD中,E是BC延长线上一点,连结AE交CD于F,则图中相似的三角形共有( )
A.1对 B.2对
C.3对 D.4对
12.下面四条线段中,不能成比例的是( )
A.3,6,2,4 B.1,,,, C.4,6,5,10 D.2,,,
13.如图,路灯距地面 ,身高 的小明从点 处沿 所在的直线行走 到点 时,人影长度
A.变长 B.变长 C.变短 D.变短
14.如图,交于点D,,,,,则的长等于( )
A. B. C. D.
15.如图,在中,于点D,有下列条件:①;②;③;④;⑤,其中一定能确定为直角三角形的条件的个数是( )
A.1 B.2 C.3 D.4
二、填空题
16.在中,,,点在边上,且,点在边上,当______时,以、、为顶点的三角形与相似.
17.如图,在△ABC中,AB>AC,D、E分别为边AB、AC上的一点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件使△FDB与△ADE相似,则添加的一个条件是_________.
18.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20,则线段x的长为________.
19.在某时刻的阳光照耀下,高为4米的旗杆在水平地面上的影长为5米,附近一个建筑物的影长为20米,则该建筑物的高为_________.
20.如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=______.
三、解答题
21.(1)四条线段a,b,c,d成比例,其中,求线段a的长.
(2)已知,且,求a的值.
22.如图,在中,,D,E分别是和上的点,.请找出中相等的角.
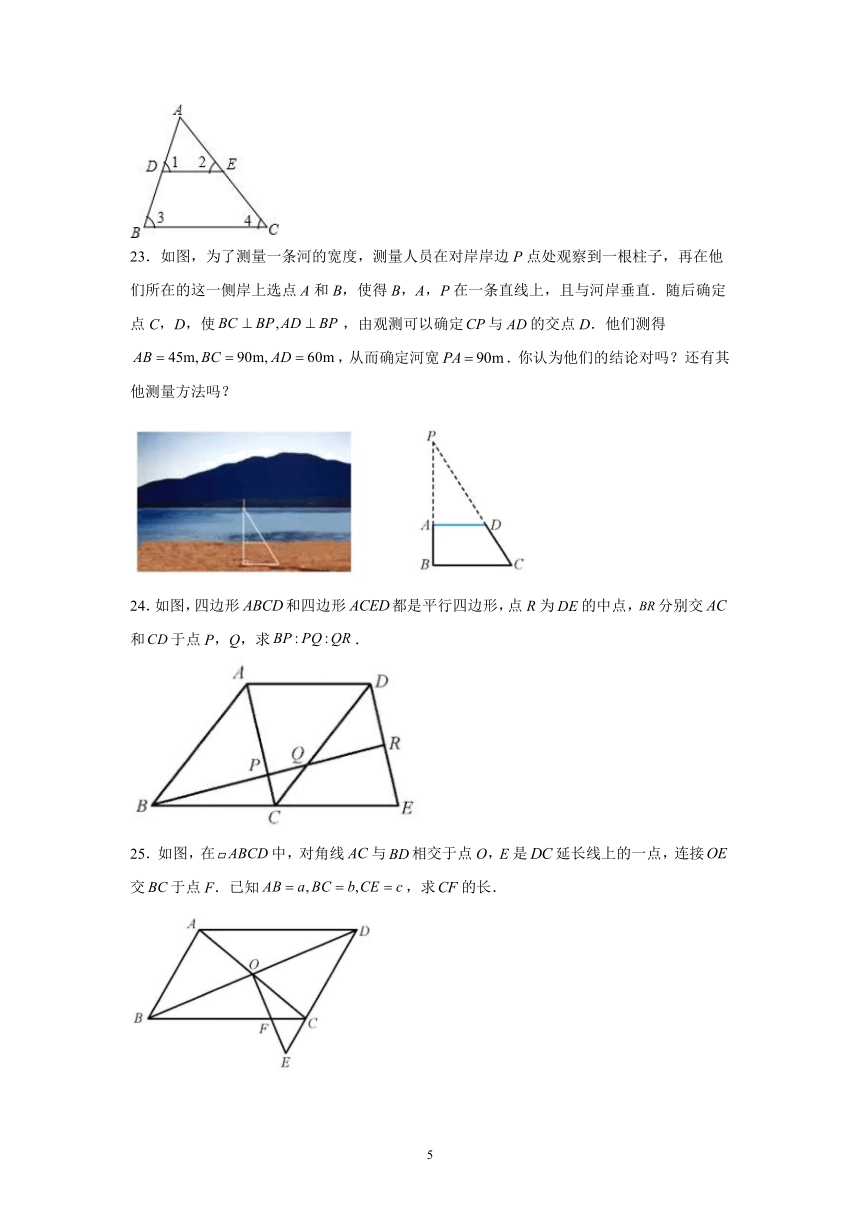
23.如图,为了测量一条河的宽度,测量人员在对岸岸边P点处观察到一根柱子,再在他们所在的这一侧岸上选点A和B,使得B,A,P在一条直线上,且与河岸垂直.随后确定点C,D,使,由观测可以确定与的交点D.他们测得,从而确定河宽.你认为他们的结论对吗?还有其他测量方法吗?
24.如图,四边形和四边形都是平行四边形,点R为的中点,分别交和于点P,Q,求.
25.如图,在中,对角线与相交于点O,E是延长线上的一点,连接交于点F.已知,求的长.
试卷第页,共页
参考答案:
1.C
解:∵交GA于点E,
,,,,
所以,A,B,D正确,
故选:C.
2.B
解:A、∵∠A=∠A,=∴△ABP∽△ACB,故本选项不符合题意;
B、根据=和∠A=∠A不能判断△ABP∽△ACB,故本选项符合题意;
C、∵∠A=∠A,∠ABP=∠C,
∴△ABP∽△ACB,故本选项不符合题意;
D、∵∠A=∠A,∠APB=∠ABC,
∴△ABP∽△ACB,故本选项不符合题意;
故选:B.
3.C
解:甲:根据题意得:AB∥A′B′,AC∥A′C′,BC∥B′C′,
∴∠A=∠A′,∠B=∠B′,
∴△ABC∽△A′B′C′,
∴甲说法正确;
乙:∵根据题意得:AB=CD=3,AD=BC=5,则A′B′=C′D′=3+2=5,A′D′=B′C′=5+2=7,
∴,
∴,
∴新矩形与原矩形不相似.
∴乙说法不正确.
故选:C.
4.C
黄金分割定义知,,所以AC2=AB.
设AB=1,AC=x,
,
解得:x=. 选C.
5.D
试题分析:本题分两种情况:
①△ADE∽△ACB
∴,
∵AB=24,AC=18,AD=12,
∴AE=16;
②△ADE∽△ABC
∴,
∵AB=24,AC=18,AD=12,
∴AE=9.
故选D.
考点:相似三角形的性质.
6.B
解:①∠B+∠DAC=90°,
故该条件无法判定△ABC是直角三角形;
②∵∠B=∠DAC,∠BAD+∠B=90°,
∴∠BAD+∠DAC=90°,即∠BAC=90°,
故该条件可以判定△ABC是直角三角形;
③,且∠ADC=∠BDA=90°,则△ADC∽△BDA,
∴∠CAD=∠ABD,
又∵∠ABD+∠BAD=90°,
∴∠BAD+∠CAD=90°,
∴该条件可以判定△ABC是直角三角形;
④∵AB2=BD BC,
∴
∵∠B=∠B,
∴△ABD∽△CBA,
∴∠BAC=∠ADC=90°,
故该条件可以判定△ABC是直角三角形;
故选:B.
7.C
解:∵△ABC∽△DEF,相似比为3:1
∴△ABC的周长:△DEF的周长=3:1
∵△ABC的周长为18
∴△DEF的周长为6.
故选:C.
8.B
因为角的度数和它的两边的长短无关,所以得到的新三角形是直角三角形,
故选B.
9.C
A、由得,,故本选项不符合题意;
B、由得,,故本选项不符合题意;
C、由得,,故本选项符合题意;
D、由得,,故本选项不符合题意;
故选:C.
10.D
∵△ABC的每条边长增加各自的10%得,
∴△ABC与的三边对应成比例,
∴△ABC∽△
∴∠=∠B.
故选D.
11.C
在平行四边形ABCD中,AB∥CD,BC∥AD,
所以,△ABE∽△FCE,△FCE∽△FDA,△ADF∽△EBA,
共3对.
故选C.
12.C
A. 3:6=2:4 ,四条线段成比例,故不符合题意;
B. 1:=:,四条线段成比例,故不符合题意;
C. 4:6≠5:10,四条线段不成比例,故符合题意;
D. 2:=:,四条线段成比例,故不符合题意,
故选C.
13.C
解:设小明在A处时影长为x,AO长为a,在B处时影长为y.
∵AC∥OP,BD∥OP,
∴△ACM∽△OPM,△BDN∽△OPN,
∴,,
则,
∴x=,y=-3.5,
∴x y=3.5,
故变短了3.5米.
故选C.
14.A
∵∠C=∠E,∠ADC=∠BDE,
∴△ADC∽△BDE,
∴,
又∵AD:DE=3:5,AE=8,
∴AD=3,DE=5,
∵BD=4,
∴,即 .
∴DC=.
故选A.
15.C
①∠1=∠A正确;
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠2+∠A=90°,
∵∠1=∠A,
∴∠1+∠2=90°,
∴∠ACB=90°,即△ABC是直角三角形;
②正确,
理由是:∵ ,∠ADC=∠BDC=90°,
∴△ADC∽△CDB,
∴∠A=∠1,
∴∠1+∠2=90°,
∴∠ACB=90°,即△ABC是直角三角形;
③错误,
理由是:∵∠BDC=90°,
∠1+∠B=90°,
∵∠2+∠B=90°,
∴∠1=∠2,不能推出∠1+∠2=90°,
∴③错误;
④正确
∵BC:AC:AB=3:4:5,
∴设BC=3k,AC=4k,AB=5k,
则BC+AC=25k,AB=25k,
即BC +AC=AB,
∴∠ACB=90°,即④正确;
⑤错误;
∵AC BD=BC CD,
∴ ,
∵∠ADC=∠BDC=90°,
无法得到△ACB是直角三角形,∴⑤错误;
正确的个数是3个.
故选C.
16.或
如解图①所示,
∵当时,
,
∴,解得;
如解图②所示,当时,
,
∴,
解得
故答案为:或.
17.∠DFB=∠ADE
解: AC=3AD,AB=3AE,∠A=∠A,
,
,
又,
.
故答案为.
18.5
解:根据题意可知m:n=x:y,即2:8=x:20,解得:x=5.
故答案为:5
19.16米
解:设该建筑物的高为米,
则
解得:
即建筑物的高度为16米
故答案为:16
20.4或6
如图1,当MN∥BC时,
则△AMN∽△ABC,
故,
则,
解得:MN=4,
如图2所示:当∠ANM=∠B时,
又∵∠A=∠A,
∴△ANM∽△ABC,
∴,
即,
解得:MN=6,
故答案为:4或6.
21.(1);(2).
解:(1)∵a,b,c,d是成比例线段
∴,
即,
∴a=1cm;
(2)设,则,
∵,
∴,解得,
∴.
22..
解:,,,,
,,
,,
,
又∵,
,
,.
23.结论对,理由见解析;有其他测量方法,见解析.
解:∵BC⊥BP,AD⊥BP,
∴ADBC,
∴△PAD∽△PBC,
∴ ,即 ,
解得:PA=90.
∴他们的结论对.
其他测量方法:如图,
在河对岸取一点A,在人所在这一侧的河岸上选B、C两点,使得AB垂直河岸,过点C作河岸的垂线段CE,从点E处观察点A,使A、E在一条直线上,且这条直线与河岸交于点D,测出BD、DC、EC的长度,然后利用相似三角形的性质求解.
24..
解:∵ACDE,
∴△PBC∽△RBE,
∴,
∴BP=PR,
又∵△PCQ∽△RDQ,
∴,
∴QR=2PQ,
∴BP:PQ:QR=3:1:2.
25..
解:过点O作OMAB,交BC于点M,
四边形ABCD是平行四边形
,
.
试卷第页,共页
一、单选题
1.如图,点G、F分别是的边、上的点,的延长线与的延长线相交于点A,交于点E,则下列结论错误的是( )
A. B. C. D.
2.如图,点P是△ABC的边AC上一点,连结BP,以下条件中,不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
3.甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对
4.已知如图,点 C 是线段 AB 的黄金分割点(AC>BC),则下列结论中正确的是( )
A.AB2=AC2+BC2 B.BC2=AC BA
C. D.
5.如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=12.在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE的长为( )
A.16 B.14 C.16或14 D.16或9
6.如图,中,于D,下列条件,①;②;③;④.其中一定能够判定是直角三角形的有( )种.
A.4 B.3 C.2 D.1
7.已知△ABC∽△DEF,相似比为3:1,且△ABC的周长为18,则△DEF的周长为( )
A.2 B.3 C.6 D.54
8.将直角三角形三边扩大同样的倍数,得到的新三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.任意三角形
9.下列比例式中,不能由得到的比例式是
A. B. C. D.
10.若的每条边长增加各自的得,则的度数与其对应角的度数相比( )
A.增加了 B.减少了 C.增加了 D.没有改变
11.如图,平行四边形ABCD中,E是BC延长线上一点,连结AE交CD于F,则图中相似的三角形共有( )
A.1对 B.2对
C.3对 D.4对
12.下面四条线段中,不能成比例的是( )
A.3,6,2,4 B.1,,,, C.4,6,5,10 D.2,,,
13.如图,路灯距地面 ,身高 的小明从点 处沿 所在的直线行走 到点 时,人影长度
A.变长 B.变长 C.变短 D.变短
14.如图,交于点D,,,,,则的长等于( )
A. B. C. D.
15.如图,在中,于点D,有下列条件:①;②;③;④;⑤,其中一定能确定为直角三角形的条件的个数是( )
A.1 B.2 C.3 D.4
二、填空题
16.在中,,,点在边上,且,点在边上,当______时,以、、为顶点的三角形与相似.
17.如图,在△ABC中,AB>AC,D、E分别为边AB、AC上的一点,AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件使△FDB与△ADE相似,则添加的一个条件是_________.
18.如果四条线段m,n,x,y成比例,若m=2,n=8,y=20,则线段x的长为________.
19.在某时刻的阳光照耀下,高为4米的旗杆在水平地面上的影长为5米,附近一个建筑物的影长为20米,则该建筑物的高为_________.
20.如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=______.
三、解答题
21.(1)四条线段a,b,c,d成比例,其中,求线段a的长.
(2)已知,且,求a的值.
22.如图,在中,,D,E分别是和上的点,.请找出中相等的角.
23.如图,为了测量一条河的宽度,测量人员在对岸岸边P点处观察到一根柱子,再在他们所在的这一侧岸上选点A和B,使得B,A,P在一条直线上,且与河岸垂直.随后确定点C,D,使,由观测可以确定与的交点D.他们测得,从而确定河宽.你认为他们的结论对吗?还有其他测量方法吗?
24.如图,四边形和四边形都是平行四边形,点R为的中点,分别交和于点P,Q,求.
25.如图,在中,对角线与相交于点O,E是延长线上的一点,连接交于点F.已知,求的长.
试卷第页,共页
参考答案:
1.C
解:∵交GA于点E,
,,,,
所以,A,B,D正确,
故选:C.
2.B
解:A、∵∠A=∠A,=∴△ABP∽△ACB,故本选项不符合题意;
B、根据=和∠A=∠A不能判断△ABP∽△ACB,故本选项符合题意;
C、∵∠A=∠A,∠ABP=∠C,
∴△ABP∽△ACB,故本选项不符合题意;
D、∵∠A=∠A,∠APB=∠ABC,
∴△ABP∽△ACB,故本选项不符合题意;
故选:B.
3.C
解:甲:根据题意得:AB∥A′B′,AC∥A′C′,BC∥B′C′,
∴∠A=∠A′,∠B=∠B′,
∴△ABC∽△A′B′C′,
∴甲说法正确;
乙:∵根据题意得:AB=CD=3,AD=BC=5,则A′B′=C′D′=3+2=5,A′D′=B′C′=5+2=7,
∴,
∴,
∴新矩形与原矩形不相似.
∴乙说法不正确.
故选:C.
4.C
黄金分割定义知,,所以AC2=AB.
设AB=1,AC=x,
,
解得:x=. 选C.
5.D
试题分析:本题分两种情况:
①△ADE∽△ACB
∴,
∵AB=24,AC=18,AD=12,
∴AE=16;
②△ADE∽△ABC
∴,
∵AB=24,AC=18,AD=12,
∴AE=9.
故选D.
考点:相似三角形的性质.
6.B
解:①∠B+∠DAC=90°,
故该条件无法判定△ABC是直角三角形;
②∵∠B=∠DAC,∠BAD+∠B=90°,
∴∠BAD+∠DAC=90°,即∠BAC=90°,
故该条件可以判定△ABC是直角三角形;
③,且∠ADC=∠BDA=90°,则△ADC∽△BDA,
∴∠CAD=∠ABD,
又∵∠ABD+∠BAD=90°,
∴∠BAD+∠CAD=90°,
∴该条件可以判定△ABC是直角三角形;
④∵AB2=BD BC,
∴
∵∠B=∠B,
∴△ABD∽△CBA,
∴∠BAC=∠ADC=90°,
故该条件可以判定△ABC是直角三角形;
故选:B.
7.C
解:∵△ABC∽△DEF,相似比为3:1
∴△ABC的周长:△DEF的周长=3:1
∵△ABC的周长为18
∴△DEF的周长为6.
故选:C.
8.B
因为角的度数和它的两边的长短无关,所以得到的新三角形是直角三角形,
故选B.
9.C
A、由得,,故本选项不符合题意;
B、由得,,故本选项不符合题意;
C、由得,,故本选项符合题意;
D、由得,,故本选项不符合题意;
故选:C.
10.D
∵△ABC的每条边长增加各自的10%得,
∴△ABC与的三边对应成比例,
∴△ABC∽△
∴∠=∠B.
故选D.
11.C
在平行四边形ABCD中,AB∥CD,BC∥AD,
所以,△ABE∽△FCE,△FCE∽△FDA,△ADF∽△EBA,
共3对.
故选C.
12.C
A. 3:6=2:4 ,四条线段成比例,故不符合题意;
B. 1:=:,四条线段成比例,故不符合题意;
C. 4:6≠5:10,四条线段不成比例,故符合题意;
D. 2:=:,四条线段成比例,故不符合题意,
故选C.
13.C
解:设小明在A处时影长为x,AO长为a,在B处时影长为y.
∵AC∥OP,BD∥OP,
∴△ACM∽△OPM,△BDN∽△OPN,
∴,,
则,
∴x=,y=-3.5,
∴x y=3.5,
故变短了3.5米.
故选C.
14.A
∵∠C=∠E,∠ADC=∠BDE,
∴△ADC∽△BDE,
∴,
又∵AD:DE=3:5,AE=8,
∴AD=3,DE=5,
∵BD=4,
∴,即 .
∴DC=.
故选A.
15.C
①∠1=∠A正确;
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠2+∠A=90°,
∵∠1=∠A,
∴∠1+∠2=90°,
∴∠ACB=90°,即△ABC是直角三角形;
②正确,
理由是:∵ ,∠ADC=∠BDC=90°,
∴△ADC∽△CDB,
∴∠A=∠1,
∴∠1+∠2=90°,
∴∠ACB=90°,即△ABC是直角三角形;
③错误,
理由是:∵∠BDC=90°,
∠1+∠B=90°,
∵∠2+∠B=90°,
∴∠1=∠2,不能推出∠1+∠2=90°,
∴③错误;
④正确
∵BC:AC:AB=3:4:5,
∴设BC=3k,AC=4k,AB=5k,
则BC+AC=25k,AB=25k,
即BC +AC=AB,
∴∠ACB=90°,即④正确;
⑤错误;
∵AC BD=BC CD,
∴ ,
∵∠ADC=∠BDC=90°,
无法得到△ACB是直角三角形,∴⑤错误;
正确的个数是3个.
故选C.
16.或
如解图①所示,
∵当时,
,
∴,解得;
如解图②所示,当时,
,
∴,
解得
故答案为:或.
17.∠DFB=∠ADE
解: AC=3AD,AB=3AE,∠A=∠A,
,
,
又,
.
故答案为.
18.5
解:根据题意可知m:n=x:y,即2:8=x:20,解得:x=5.
故答案为:5
19.16米
解:设该建筑物的高为米,
则
解得:
即建筑物的高度为16米
故答案为:16
20.4或6
如图1,当MN∥BC时,
则△AMN∽△ABC,
故,
则,
解得:MN=4,
如图2所示:当∠ANM=∠B时,
又∵∠A=∠A,
∴△ANM∽△ABC,
∴,
即,
解得:MN=6,
故答案为:4或6.
21.(1);(2).
解:(1)∵a,b,c,d是成比例线段
∴,
即,
∴a=1cm;
(2)设,则,
∵,
∴,解得,
∴.
22..
解:,,,,
,,
,,
,
又∵,
,
,.
23.结论对,理由见解析;有其他测量方法,见解析.
解:∵BC⊥BP,AD⊥BP,
∴ADBC,
∴△PAD∽△PBC,
∴ ,即 ,
解得:PA=90.
∴他们的结论对.
其他测量方法:如图,
在河对岸取一点A,在人所在这一侧的河岸上选B、C两点,使得AB垂直河岸,过点C作河岸的垂线段CE,从点E处观察点A,使A、E在一条直线上,且这条直线与河岸交于点D,测出BD、DC、EC的长度,然后利用相似三角形的性质求解.
24..
解:∵ACDE,
∴△PBC∽△RBE,
∴,
∴BP=PR,
又∵△PCQ∽△RDQ,
∴,
∴QR=2PQ,
∴BP:PQ:QR=3:1:2.
25..
解:过点O作OMAB,交BC于点M,
四边形ABCD是平行四边形
,
.
试卷第页,共页
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
