广东省四校2021-2022学年高三上学期12月第一次联考数学试卷(PDF版含答案)
文档属性
| 名称 | 广东省四校2021-2022学年高三上学期12月第一次联考数学试卷(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 978.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 10:01:03 | ||
图片预览




文档简介
2022届广东省四校高三第一次联考
数学试题
考试时间 120分钟,总分 150分
注意事项:
1.答题前,先将自己的姓名、准考证号等相关信息填写在试卷和答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用 2B铅笔把答题卡上对应题目的答案标号涂黑,写在试
卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色字迹的签字笔或钢笔直接答在答题卡上对应的答题区域内,写在试
卷、草稿纸和答题卡上的非答题区域均无效。
4.考生必须保持答题卡的整洁。考试结束后,请将本试卷和答题卡一并上交。
第Ⅰ卷(选择题)
一、单选题(本题共 8小题,每小题 5分,共 40分。在每小题给出的四个选项中,只有一项符合题
目要求。)
1.设全集U {x|x 0},M x | x2 x 0 N y | y 2x, , x 0 ,则M CU N ( )
A. 0, B. 1, C. 0,1 D. 0,1
2 mi
2.已知复数 z 为纯虚数,则实数m ( )
2 i
A. 1 B. 4 C.1 D.4
3.将函数 f (x) sin 3x 的图象向左平移 个单位长度,再将得到的图象上的所有点的横坐标
4 3
变为原来的 2倍(纵坐标不变),最后得到函数 g x 的图象,则 g x ( )
3 3 3 3
A. sin x B.sin 6x C.sin x D.sin 6x
2 12 12 2 4 4
4.已知 y 与 x 之间的线性回归方程为 y 1.6x 21,其样本点的中心为 (x,37) ,样本数据中 x 的取
值依次为2 ,6 ,8 ,16,m ,则m ( )
A.12 B.16 C.18 D.20
5.如图为陕西博物馆收藏的国宝——唐·金筐宝钿团花纹金杯,杯身曲
线内收,玲珑娇美,巧夺天工,是唐代金银细作的典范之作.该杯的主
x2 y2
体部分可以近似看作是双曲线C : 1(a 0,b 0)的右支与
a2 b2
2022 届广东省四校第一次联考数学试题第 1 页 共 6 页
直线 x 0 , y 4 , y 2围成的曲边四边形 ABMN 绕 y 轴旋转一周得到的几何体,若该金杯主
57 21
体部分的上口外半径BM 为 ,下底外半径 AN 为 ,则双曲线C 的离心率为( )
3 3
A.3 B. 3 C. 2 D.2
6.已知抛物线C : x2 4y 的焦点为F ,准线为 l .点P 在C 上,直线PF 交 x 轴于点Q ,若
PF 3FQ ,则点P 到准线 l 的距离为( )
A.6 B.5 C.4 D.3
n a a a a
7.已知数列 an 满足an ,则a
2 3 2020 2021
1 ( ) 2 2 2
n 1 2 3 2020 20212
2020 2018 2019 2021
A. B. C. D.
2021 2019 2020 2022
8.已知实数a,b,c 0,e ,且2a a2,3b b3,5c c5 ,则( )
A.c a b B.a c b C.b c a D.b a c
二、多选题(本题共 4小题,每小题 5分,共 20分。在每小题给出的选项中,有多项符合题目要求。
全部选对的得 5分,部分选对的得 2分,有选错的得 0分。)
9.下列说法中,正确的是( )
x
A.若命题 p : x R,ex x 1,则 p : x 00 R,e x0 1
3
B.函数 f (x) x (x 0) 的最小值为2 3 3
x 3
C.已知a x 2,3 ,b x,1 ,且 a 与b 共线,则 x 1
2x 1
D.函数 f (x) 既是奇函数,又是定义域上的增函数
2x 1
10.已知直线 l : kx y k 1 0和圆O : x2 y2 16 ,则( )
A.直线 l 恒过定点 1,1
B.若 k 1,则直线 l 被圆O截得的弦长为2 2
C.存在 k 使得直线 l 与直线 l0 : x 2y 2 0垂直
D.直线 l 与圆O相交
2022 届广东省四校第一次联考数学试题第 2 页 共 6 页
11.下列事件中, A ,B 不.是.独立事件的是( )
A.抛掷一枚质地均匀的硬币两次, A “第一次为正面向上”,B “第二次为反面向上”
B.袋中有大小相同的两个白球和两个黑球,从中不放回地摸出两球, A “第一次摸到白
球”,B “第二次摸到白球”
C.从一副除大小王的 52张扑克牌中任取一张, A “抽到 J”,B “抽到的牌是黑色的”
D. A “电灯泡能使用 100小时”,B “电灯泡能使用 1000小时”
12.在长方体 ABCD A1B1C1D1 中, AB AD 1, AA1 2 , P 是线段 BC1 上的一动点,则下列说
法中正确的是( )
A. A1P / /平面AD1C
5
B. A1P 与平面BCC1B1所成角的正切值的最大值是
2
C. A1P PC 的最小值为 5
D.以 A为球心, 2 为半径的球面与侧面DCC1D1的交线长是
2
第Ⅱ卷(非选择题)
三、填空题(本题共 4小题,每小题 5分,共 20分。其中第 16题第一空 2分,第二空 3分。)
13.已知函数 f x loga x 1 1 a 0,a 1 的图象恒过点 A ,若点 A在角 的终边上,则
sin 2 ________.
2 a x 1, x 2
14.已知函数 f x ,若函数 f x 在R 上单调递增,则实数a 的取值范围是
ax 1 , x 2
________.
15.在三棱锥 P ABC中, ABC 和 PBC 都是边长为 2 3 的正三角形, PA 3 2 ,则三棱锥
P ABC 的外接球的表面积为________.
16.我国魏晋时期的科学家刘徽创立了“割圆术”,实施“以直代曲”的近似计算,用正n 边形进行“内
外夹逼”的办法求出了圆周率 的精度较高的近似值,这是我国最优秀的传统科学文化之一.借用
“以直代曲”的近似计算方法,在切点附近,可以用函数图象的切线近似代替在切点附近的曲线来
近似计算.设 f (x) ln x ,则曲线 y f x 在点 1,0 处的切线方程为________,用此结论近似
计算 4000 e 的值为________(结果用分数表示).
2022 届广东省四校第一次联考数学试题第 3 页 共 6 页
四、解答题(本题共 6小题,共 70分。解答应写出文字说明、证明过程或演算步骤。)
17.(本小题满分 10分)
在①2acos A ccos B bcosC ;②asin B bsin A .
3
这两个条件中任选一个,补充在下面问题中,并解答.
3 3
已知 ABC的内角 A, B,C 的对边分别为a,b,c .若 ABC的面积 S ,c 2, ▲ ,
2
求 a .
注:如果选择多个条件分别解答,按第一个解答计分.
18.(本小题满分 12分)
北京冬季奥运会将于 2022年 2月 4日至 2022年 2月 20日在中华人民共和国北京市和河北省张
家口市联合举行.这是中国历史上第一次举办冬季奥运会,北京、张家口同为主办城市,也是中国继北
京奥运会、南京青奥会之后第三次举办奥运赛事.北京冬奥组委对报名参加北京冬奥会志愿者的人员
开展冬奥会志愿者的培训活动,并在培训结束后进行了一次考核.为了解本次培训活动的效果,从中
随机抽取 80名志愿者的考核成绩,根据这 80名志愿者的考核成绩得到的统计图表如下所示.
女志愿者考核成绩频率分布表 男志愿者考核成绩频率分布直方图
若参加这次考核的志愿者考核成绩在[90,100]内,则考核等级为优秀.
(1)分别求出m,a,b的值,以及这次培训考核等级为优秀的男志愿者人数;
(2)若从样本中考核等级为优秀的志愿者中随机抽取3人进行学习心得分享,记抽到男志愿者
的人数为 X ,求 X 的分布列及数学期望.
2022 届广东省四校第一次联考数学试题第 4 页 共 6 页
19.(本小题满分 12分)
设数列 an 的前 n 项和为 S ,且满足 3an 2Sn (2 n N ) , bn 是公差不为 0 的等差数n
列,b b1 1, 4是b2与b8 的等比中项.
(1)求数列 an 和 bn 的通项公式;
an ,n为偶数
(2)对任意的正整数n ,设 cn ,求数列 cn 的前2n项和T2n .
bn 2 ,n为奇数
20.(本小题满分 12分)
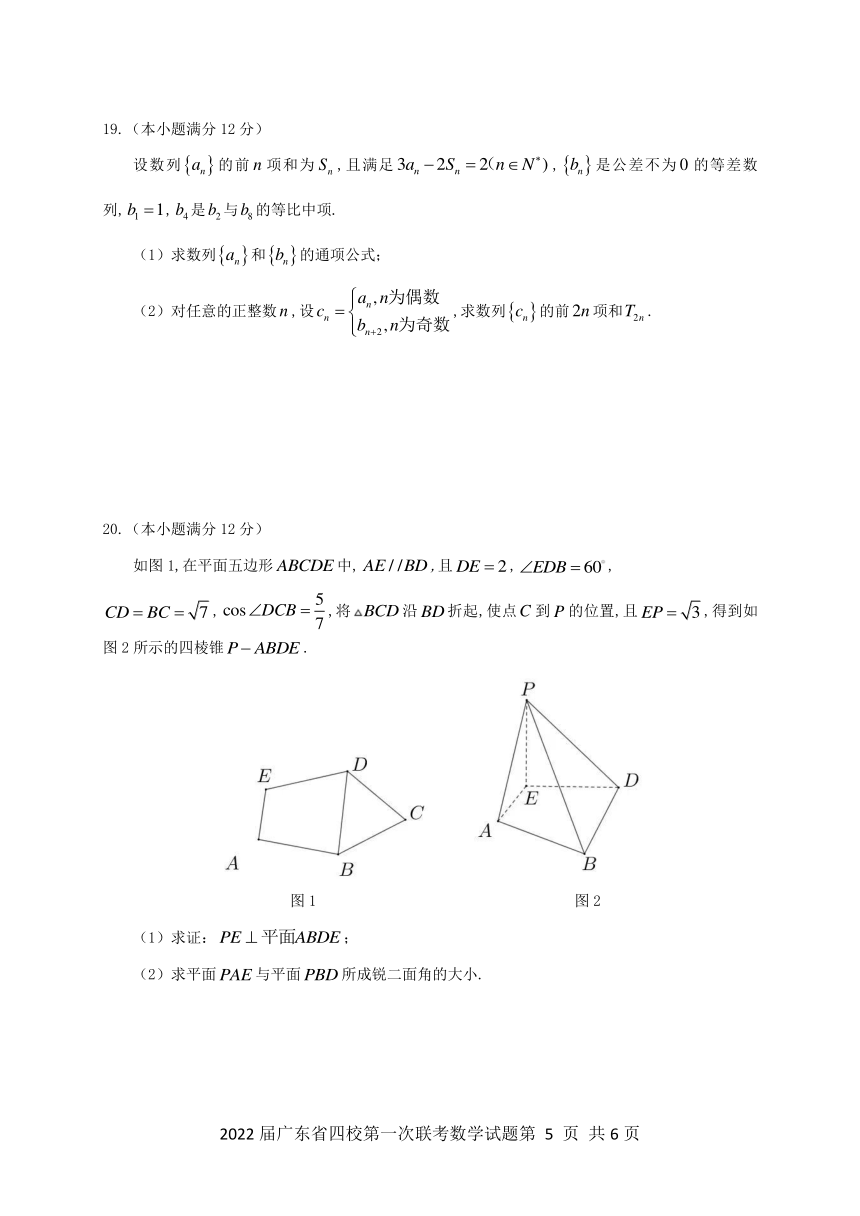
如图 1,在平面五边形 ABCDE中, AE / /BD ,且DE 2 , EDB 60 ,
5
CD BC 7 , cos DCB ,将 BCD 沿 BD折起,使点C 到 P 的位置,且 EP 3 ,得到如
7
图 2 所示的四棱锥P ABDE .
图 1 图 2
(1)求证:PE 平面ABDE ;
(2)求平面PAE 与平面PBD所成锐二面角的大小.
2022 届广东省四校第一次联考数学试题第 5 页 共 6 页
21.(本小题满分 12分)
x2 y2
已知椭圆C : 1 a b 0 的左,右焦点分别为 F1 , F2 ,椭圆C 上任意一点 P 到焦点
a2 b2
距离的最大值是最小值的3倍,且通径长为3(椭圆的通径:过椭圆的焦点且垂直于长轴的弦).
(1)求椭圆C 的标准方程;
(2) 过F 的直线 l 与椭圆C 相交于不同的两点2 A , B ,则 ABF 的内切圆面积是否存在最大值 1
若存在,则求出最大值;若不存在,请说明理由.
22.(本小题满分 12分)
已知a R , f x x e ax (其中e为自然对数的底数).
(1)讨论函数 y f x 的单调性;
(2)若a 0 ,函数 y f x a 有两个零点 x1, x2 ,求证: x1 x2 2 e .
2022 届广东省四校第一次联考数学试题第 6 页 共 6 页
2022 届广东省四校高三第一次联考
数学参考答案及评分标准
一、单选题(本题共 8小题,每小题 5分,共 40分。在每小题给出的四个选项中,只有一项符合题目
要求。)
题目 1 2 3 4 5 6 7 8
答案 D B C C D B D A
第 8 题详细解答如下:
由2a a2,3b b3,5c c5 ,得a ln 2 2lna ,b ln3 3lnb ,c ln5 5lnc ,即
ln 2 ln a ln3 lnb ln5 ln c
, , .
2 a 3 b 5 c
ln x
设函数 f x ,则 f 2 f a , f 3 f b , f 5 f c .
x
1 ln x
又 f x ,由 f x 0,得 x e,则 f x 在 0,e 上单调递增,在 e, 上单调递减,故
x2
f 3 f 4 f 5 .
又 f 2 f 4 ,所以 f 3 f 2 f 5 ,即 f b f a f c .
因为a,b,c 0,e ,所以c a b ,故选 A.
二、多选题(本题共 4小题,每小题 5分,共 20分。在每小题给出的选项中,有多项符合题目要求。
全部选对的得 5分,部分选对的得 2分,有选错的得 0分。)
题目 9 10 11 12
答案 ACD CD BD ABD
第 12题详细解答如下:
对于 A,由于平面 A1BC1 / / 平面 AD1C ,所以 A1P / / 平面 AD1C ,所以 A正确;
5
对于 B,当B1P BC1时, A1P 与平面BCC1B1所成角的正切值最大,最大值是 ,所以 B正确;
2
对于 C,将 A1C1B 沿BC1翻折与 BCC1在同一个平面,且点 A1,C 在直线BC1的异侧,此时
2 170 170
cos AC C ,则 AC ,所以 A1P PC 的最小值为 ,所以 C不正确; 1 1 1
10 5 5
对于 D,由于 AD 平面DCC1D1 ,所以交线为以D为圆心,半径为 1 的四分之一圆周,所以交线长为
2022届广东省四校第一次联考数学参考答案 第 1 页 共 8 页
,所以 D正确.故选:ABD.
2
三、填空题(本题共 4小题,每小题 5分,共 20分。其中第 16题第一空 2分,第二空 3分。)
题目 13 14 15 16
4001
4 5 y x 1
答案 , 2 20 4000
5 3
(此空 2分) (此空 3分)
第 15题详细解答如下:
设 BC 中点为T , ABC的外心为O1, PBC 的外心为O2 ,过点O1作平面 ABC 的垂线,过点O2 作
平面PBC 的垂线,两条垂线的交点O即为三棱锥P ABC 外接球的球心.
因为 ABC和 PBC 都是边长为2 3的正三角形,可得PT AT 3.
PA 3 2 2又 ,所以 AT PT 2 AP2 ,所以PT AT .
又因为BC AT ,PT BC T ,所以 AT 平面PBC .
1 1
因为 AT 平面 ABC ,所以平面PBC 平面 ABC ,且TO1 AT 1,TO2 PT 1
3 3
所以四边形OO1TO
2 2
2 是边长为 1的正方形,所以外接球半径R OP OO2 O2P 1 4 5 ,
故外接球的表面积为 S 4 R2 20 .
第 16题详细解答如下:
1
由题意,得 f x ,则 f 1 1,故所求切线方程为 y x 1;
x
因为 1 与 1 之间的距离比较小,因此在切点附近用切线代替曲线,近似计算,得
4000 e e4000
1 1 1 1 1
4000 1 4001f e ln e
4000 e4000 1,即e4000 ln e4000 1 1 .
4000 4000
2022届广东省四校第一次联考数学参考答案 第 2 页 共 8 页
四、解答题(本题共 6小题,共 70分。解答应写出文字说明、证明过程或演算步骤。)
17.(本小题满分 10分)
选择条件①.
因为2acos A ccos B bcosC ,
根据正弦定理,得2sin Acos A sinCcosB sin BcosC ,…………………………1分
即2sin Acos A sin B C sin A sin A,…………………………2分
1
因为 A 0, ,所以sin A 0 ,所以cos A ,所以 A .…………………………4分
2 3
1 1 3 3
由 S ABC bcsin A b 2sin ,…………………………6分
2 2 3 2
解得b 3 1.…………………………7分
2 1
根据余弦定理,得a b2 c2 2bccos A 4 2 3 4 2 3 1 2 6,………………9分
2
所以a 6 .…………………………10分
选择条件②.
因为asin B bsin A ,根据正弦定理,得sin Asin B sin Bsin A ……………1分
3 3
1 3
由 B 0, ,得sin B 0 ,所以sin A sin A sin A cos A,……………………2分
3 2 2
sin A
则 tan A 3 .…………………………3分
cos A
又 A 0, ,所以 A .…………………………4分
3
1 1 3 3
由 S ABC bcsin A b 2sin ,…………………………6分
2 2 3 2
解得b 3 1.…………………………7分
2 2 2 1
根据余弦定理,得a b c 2bccos A 4 2 3 4 2 3 1 2 6,………………9分
2
所以a 6 .…………………………10分
2022届广东省四校第一次联考数学参考答案 第 3 页 共 8 页
18.(本小题满分 12分)
(1)由女志愿者考核成绩的频率分布表可知被抽取的女志愿者的人数为2 0.050 40 .
因为0.050 0.325 m 0.100 0.075 1,所以m 0.45.…………………………1分
所以a 40 0.100 4,b 40 0.075 3.…………………………3分
因为被抽取的志愿者人数是 80,所以被抽取的男志愿者人数是80 40 40 .
由男志愿者考核成绩频率分布直方图可知男志愿者这次培训考核等级为优秀的频率为
0.010 0.015 5 0.125,则这次培训考核等级为优秀的男志愿者人数为40 0.125 5.…4分
(2)由题可知,这次培训考核等级为优秀的女志愿者人数为4 3 7 ,故样本中考核等级为优秀的志
愿者人数为5 7 12 ,则 X 的可能取值为 0,1,2,3. …………………………6分
C3 35 7
P X 0 7 …………………………7分
C312 220 44
C15C
2
7 105 21P X 1 …………………………8分
C312 220 44
C2 15 C7 70 7P X 2 …………………………9分
C312 220 22
C3 10 1
P X 3 5 …………………………10分
C312 220 22
所以 X 的分布列为
X 0 1 2 3
7 21 7 1
P
44 44 22 22
…………………………11分
7 21 7 1 5
故 EX 0 1 2 3 .…………………………12分
44 44 22 22 4
19.(本小题满分 12分)
(1)因为3an 2Sn 2 n N ,所以,当n 2时,3an 1 2Sn 1 2 ,
a
所以3 an an 1 2 Sn Sn 1 0 ,所以3 an an 1 2an 0,即
n 3 n 2 .………2分
an 1
当 n 1时,3a1 2S1 2,
又 S1 a1,所以a1 2,…………………………3分
2022届广东省四校第一次联考数学参考答案 第 4 页 共 8 页
所以数列 an 是以 2为首项,3为公比的等比数列.
n 1
所以an 2 3 .…………………………4分
设等差数列 bn 的公差为d ,d 0 .
2
因为b 1,b4是b 与b 的等比中项,所以b4 b2b8 ,…………………………5分 1 2 8
2
即 1 3d 1 d 1 7d ,解得d 1或d 0 (舍去).…………………………6分
所以bn 1 n 1 1 n.…………………………7分
n 1
2 3 ,n为偶数
(2)由题意,得 cn .…………………………8分
n 2,n为奇数
所以T2n c1 c3 c2n 1 c2 c4 c2n …………………………9分
3 5 2n 1 2 3
1 33 32n 1 …………………………10分
3 2n 1 n 3 1 9n
2 …………………………11分
2 1 9
3 9n 1
n2 2n …………………………12分
4
20.(本小题满分 12分)
5
(1)在 BCD中,CD BC 7 ,cos DCB ,
7
5
由余弦定理,得BD CD2 BC2 2CD BC cos DCB 7 7 2 7 7 2.…1分
7
连结BE ,因为BD DE 2, EDB 60 ,所以BE 2.…………………………2分
又因为EP 3 ,故在 PBE中, EP2 BE2 PB2 ,所以PE BE .…………………………3分
同理可证PE DE .…………………………4分
因为BE DE E , BE , DE 平面 ABDE ,所以PE 平面 ABDE .…………………………5分
2022届广东省四校第一次联考数学参考答案 第 5 页 共 8 页
(2)以E 为坐标原点,EA , EP所在直线为 x 轴,z 轴建立如图所示
空间直角坐标系E xyz ,
则 P 0,0, 3 ,B 1, 3,0 , D 1, 3,0 .………………………6分
所以PB 1, 3, 3 , BD 2,0,0 …………………………7分
n PB x 3y 3z 0
设平面PBD的一个法向量为n x, y, z ,则 .……………………8分
n BD 2x 0
令 y 1,则 z 1, x 0 ,故n 0,1,1 .…………………………9分
又平面PAE 的一个法向量为m 0,1,0 ,…………………………10分
n m 1 2
所以 cos n,m ,…………………………11分
n m 2 2
故平面PAE 与平面PBD所成锐二面角的大小为 .…………………………12分
4
注:使用几何法求解第(2)问同样给分.
21.(本小题满分 12分)
(1)因为椭圆C 上任意一点P 到焦点距离的最大值是最小值的3倍,
所以a c 3 a c ,即a 2c .…………………………1分
2b2
因为过焦点且垂直于长轴的弦长为3 ,所以 3.…………………………2分
a
又a2 b2 c2 ,联立方程组,解得a 2,b 3,c 1.…………………………3分
x2 y2
故椭圆C 的标准方程为 1.…………………………4分
4 3
1
(2)设 ABF1的内切圆半径为 r ,则 S ABF AF1 AB BF r . 1 12
又因为 AF1 AB BF1 8 ,所以 S ABF 4r .…………………………5分 1
要使得 ABF1的内切圆面积最大,只需 S ABF 的值最大. 1
由题意,得直线 l 斜率不为0 ,故设 A x1, y1 , B x2 , y2 ,直线 l : x my 1.
2022届广东省四校第一次联考数学参考答案 第 6 页 共 8 页
x2 y2
1
由 4 3 ,得 3m2 4 y2 6my 9 0.…………………………6分
x my 1
6m
y1 y2 3m2 4
所以 .…………………………7分
9y1y2 2
3m 4
1 2
所以 S ABF F1F2 y1 y2 y1 y2 4y1 1y2 2
36m2 36 12 m2 1
…………………………8分
2 2
3m2 4 3m 4 3 m
2 1 1
2 12t 12
设 t m 1 1,则 S ABF .…………………………9分 1 3t2 1 1
3t
t
1 1
设 f t 3t , t 1,则 f t 3 0 ,故 f2 t 在 1, 上单调递增.…………………10分 t t
3
所以当 t 1,即m 0时, S ABF 的最大值为3 ,此时 r .…………………………11分 1 4
9
所以 ABF1的内切圆面积最大值为 .…………………………12分
16
22.(本小题满分 12分)
(1)由题意,得 f x e ax ax e ax e ax 1 ax …………………………1分
①当a 0时, f x 1 0,则 f x 在 , 上单调递增.…………………………2分
1
②当a 0时,由 f x 0,得 x .
a
1 1
若 a 0 ,则 x , , f x 0; x , , f x 0;…………………………3分
a a
1 1
若 a 0则 x , , f x 0; x , , f x 0.…………………………4分
a a
综上,得
当 a 0时, f x 在 , 上单调递增;
1 1
当 a 0时, f x 在 , 上单调递减,在 , 上单调递增;
a a
2022届广东省四校第一次联考数学参考答案 第 7 页 共 8 页
1 1
当 a 0时, f x 在 , 上单调递增,在 , 上单调递减.…………………………5分
a a
1 1
(2)由(1)知,当a 0时, f x 在 , 上单调递增,在 , 上单调递减.
a a
1 1 1
且当 x 时, f x 0 , f x 有极大值 f .
a a ae
1 1
因为a 0,函数 y f x a 有两个零点 x 21, x2 ,所以a ,即a .……………………6分
ae e
1 2 2
不妨设 x1 x2 ,则0 x1 x2 .先证 x1 x2 ,即证 x1 x2 .…………………………7分
a a a
1 2 1 1 2
因为 x1 , x2 ,且 f x 在 , 上单调递增,所以即证 f x1 f x . 2
a a a a a
2
又 f x1 f x2 ,所以即证 f x f x . 2 2
a
2 2
F x f x f x x e ax x e 2 ax
1
令 , x , .…………………………8分
a a a
2
则 F x e ax 1 ax e 2 ax 1 a x 1 ax e
ax e 2 ax …………………………9分
a
1
x , , ax ax 2 ,1 ax 0,故F x 1 ax e
ax e 2 ax 0
a
2 1
所以函数F x f x f x 在 , 上单调递增.
a a
1
所以F x F 0 .…………………………10分
a
1 2 2
因为 x2 ,所以 f x2 f x2 ,即 x1 x2 .…………………………11分
a a a
1 2
又 a2 ,即 2 e ,
e a
所以 x1 x2 2 e .…………………………12分
2022届广东省四校第一次联考数学参考答案 第 8 页 共 8 页
数学试题
考试时间 120分钟,总分 150分
注意事项:
1.答题前,先将自己的姓名、准考证号等相关信息填写在试卷和答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用 2B铅笔把答题卡上对应题目的答案标号涂黑,写在试
卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色字迹的签字笔或钢笔直接答在答题卡上对应的答题区域内,写在试
卷、草稿纸和答题卡上的非答题区域均无效。
4.考生必须保持答题卡的整洁。考试结束后,请将本试卷和答题卡一并上交。
第Ⅰ卷(选择题)
一、单选题(本题共 8小题,每小题 5分,共 40分。在每小题给出的四个选项中,只有一项符合题
目要求。)
1.设全集U {x|x 0},M x | x2 x 0 N y | y 2x, , x 0 ,则M CU N ( )
A. 0, B. 1, C. 0,1 D. 0,1
2 mi
2.已知复数 z 为纯虚数,则实数m ( )
2 i
A. 1 B. 4 C.1 D.4
3.将函数 f (x) sin 3x 的图象向左平移 个单位长度,再将得到的图象上的所有点的横坐标
4 3
变为原来的 2倍(纵坐标不变),最后得到函数 g x 的图象,则 g x ( )
3 3 3 3
A. sin x B.sin 6x C.sin x D.sin 6x
2 12 12 2 4 4
4.已知 y 与 x 之间的线性回归方程为 y 1.6x 21,其样本点的中心为 (x,37) ,样本数据中 x 的取
值依次为2 ,6 ,8 ,16,m ,则m ( )
A.12 B.16 C.18 D.20
5.如图为陕西博物馆收藏的国宝——唐·金筐宝钿团花纹金杯,杯身曲
线内收,玲珑娇美,巧夺天工,是唐代金银细作的典范之作.该杯的主
x2 y2
体部分可以近似看作是双曲线C : 1(a 0,b 0)的右支与
a2 b2
2022 届广东省四校第一次联考数学试题第 1 页 共 6 页
直线 x 0 , y 4 , y 2围成的曲边四边形 ABMN 绕 y 轴旋转一周得到的几何体,若该金杯主
57 21
体部分的上口外半径BM 为 ,下底外半径 AN 为 ,则双曲线C 的离心率为( )
3 3
A.3 B. 3 C. 2 D.2
6.已知抛物线C : x2 4y 的焦点为F ,准线为 l .点P 在C 上,直线PF 交 x 轴于点Q ,若
PF 3FQ ,则点P 到准线 l 的距离为( )
A.6 B.5 C.4 D.3
n a a a a
7.已知数列 an 满足an ,则a
2 3 2020 2021
1 ( ) 2 2 2
n 1 2 3 2020 20212
2020 2018 2019 2021
A. B. C. D.
2021 2019 2020 2022
8.已知实数a,b,c 0,e ,且2a a2,3b b3,5c c5 ,则( )
A.c a b B.a c b C.b c a D.b a c
二、多选题(本题共 4小题,每小题 5分,共 20分。在每小题给出的选项中,有多项符合题目要求。
全部选对的得 5分,部分选对的得 2分,有选错的得 0分。)
9.下列说法中,正确的是( )
x
A.若命题 p : x R,ex x 1,则 p : x 00 R,e x0 1
3
B.函数 f (x) x (x 0) 的最小值为2 3 3
x 3
C.已知a x 2,3 ,b x,1 ,且 a 与b 共线,则 x 1
2x 1
D.函数 f (x) 既是奇函数,又是定义域上的增函数
2x 1
10.已知直线 l : kx y k 1 0和圆O : x2 y2 16 ,则( )
A.直线 l 恒过定点 1,1
B.若 k 1,则直线 l 被圆O截得的弦长为2 2
C.存在 k 使得直线 l 与直线 l0 : x 2y 2 0垂直
D.直线 l 与圆O相交
2022 届广东省四校第一次联考数学试题第 2 页 共 6 页
11.下列事件中, A ,B 不.是.独立事件的是( )
A.抛掷一枚质地均匀的硬币两次, A “第一次为正面向上”,B “第二次为反面向上”
B.袋中有大小相同的两个白球和两个黑球,从中不放回地摸出两球, A “第一次摸到白
球”,B “第二次摸到白球”
C.从一副除大小王的 52张扑克牌中任取一张, A “抽到 J”,B “抽到的牌是黑色的”
D. A “电灯泡能使用 100小时”,B “电灯泡能使用 1000小时”
12.在长方体 ABCD A1B1C1D1 中, AB AD 1, AA1 2 , P 是线段 BC1 上的一动点,则下列说
法中正确的是( )
A. A1P / /平面AD1C
5
B. A1P 与平面BCC1B1所成角的正切值的最大值是
2
C. A1P PC 的最小值为 5
D.以 A为球心, 2 为半径的球面与侧面DCC1D1的交线长是
2
第Ⅱ卷(非选择题)
三、填空题(本题共 4小题,每小题 5分,共 20分。其中第 16题第一空 2分,第二空 3分。)
13.已知函数 f x loga x 1 1 a 0,a 1 的图象恒过点 A ,若点 A在角 的终边上,则
sin 2 ________.
2 a x 1, x 2
14.已知函数 f x ,若函数 f x 在R 上单调递增,则实数a 的取值范围是
ax 1 , x 2
________.
15.在三棱锥 P ABC中, ABC 和 PBC 都是边长为 2 3 的正三角形, PA 3 2 ,则三棱锥
P ABC 的外接球的表面积为________.
16.我国魏晋时期的科学家刘徽创立了“割圆术”,实施“以直代曲”的近似计算,用正n 边形进行“内
外夹逼”的办法求出了圆周率 的精度较高的近似值,这是我国最优秀的传统科学文化之一.借用
“以直代曲”的近似计算方法,在切点附近,可以用函数图象的切线近似代替在切点附近的曲线来
近似计算.设 f (x) ln x ,则曲线 y f x 在点 1,0 处的切线方程为________,用此结论近似
计算 4000 e 的值为________(结果用分数表示).
2022 届广东省四校第一次联考数学试题第 3 页 共 6 页
四、解答题(本题共 6小题,共 70分。解答应写出文字说明、证明过程或演算步骤。)
17.(本小题满分 10分)
在①2acos A ccos B bcosC ;②asin B bsin A .
3
这两个条件中任选一个,补充在下面问题中,并解答.
3 3
已知 ABC的内角 A, B,C 的对边分别为a,b,c .若 ABC的面积 S ,c 2, ▲ ,
2
求 a .
注:如果选择多个条件分别解答,按第一个解答计分.
18.(本小题满分 12分)
北京冬季奥运会将于 2022年 2月 4日至 2022年 2月 20日在中华人民共和国北京市和河北省张
家口市联合举行.这是中国历史上第一次举办冬季奥运会,北京、张家口同为主办城市,也是中国继北
京奥运会、南京青奥会之后第三次举办奥运赛事.北京冬奥组委对报名参加北京冬奥会志愿者的人员
开展冬奥会志愿者的培训活动,并在培训结束后进行了一次考核.为了解本次培训活动的效果,从中
随机抽取 80名志愿者的考核成绩,根据这 80名志愿者的考核成绩得到的统计图表如下所示.
女志愿者考核成绩频率分布表 男志愿者考核成绩频率分布直方图
若参加这次考核的志愿者考核成绩在[90,100]内,则考核等级为优秀.
(1)分别求出m,a,b的值,以及这次培训考核等级为优秀的男志愿者人数;
(2)若从样本中考核等级为优秀的志愿者中随机抽取3人进行学习心得分享,记抽到男志愿者
的人数为 X ,求 X 的分布列及数学期望.
2022 届广东省四校第一次联考数学试题第 4 页 共 6 页
19.(本小题满分 12分)
设数列 an 的前 n 项和为 S ,且满足 3an 2Sn (2 n N ) , bn 是公差不为 0 的等差数n
列,b b1 1, 4是b2与b8 的等比中项.
(1)求数列 an 和 bn 的通项公式;
an ,n为偶数
(2)对任意的正整数n ,设 cn ,求数列 cn 的前2n项和T2n .
bn 2 ,n为奇数
20.(本小题满分 12分)
如图 1,在平面五边形 ABCDE中, AE / /BD ,且DE 2 , EDB 60 ,
5
CD BC 7 , cos DCB ,将 BCD 沿 BD折起,使点C 到 P 的位置,且 EP 3 ,得到如
7
图 2 所示的四棱锥P ABDE .
图 1 图 2
(1)求证:PE 平面ABDE ;
(2)求平面PAE 与平面PBD所成锐二面角的大小.
2022 届广东省四校第一次联考数学试题第 5 页 共 6 页
21.(本小题满分 12分)
x2 y2
已知椭圆C : 1 a b 0 的左,右焦点分别为 F1 , F2 ,椭圆C 上任意一点 P 到焦点
a2 b2
距离的最大值是最小值的3倍,且通径长为3(椭圆的通径:过椭圆的焦点且垂直于长轴的弦).
(1)求椭圆C 的标准方程;
(2) 过F 的直线 l 与椭圆C 相交于不同的两点2 A , B ,则 ABF 的内切圆面积是否存在最大值 1
若存在,则求出最大值;若不存在,请说明理由.
22.(本小题满分 12分)
已知a R , f x x e ax (其中e为自然对数的底数).
(1)讨论函数 y f x 的单调性;
(2)若a 0 ,函数 y f x a 有两个零点 x1, x2 ,求证: x1 x2 2 e .
2022 届广东省四校第一次联考数学试题第 6 页 共 6 页
2022 届广东省四校高三第一次联考
数学参考答案及评分标准
一、单选题(本题共 8小题,每小题 5分,共 40分。在每小题给出的四个选项中,只有一项符合题目
要求。)
题目 1 2 3 4 5 6 7 8
答案 D B C C D B D A
第 8 题详细解答如下:
由2a a2,3b b3,5c c5 ,得a ln 2 2lna ,b ln3 3lnb ,c ln5 5lnc ,即
ln 2 ln a ln3 lnb ln5 ln c
, , .
2 a 3 b 5 c
ln x
设函数 f x ,则 f 2 f a , f 3 f b , f 5 f c .
x
1 ln x
又 f x ,由 f x 0,得 x e,则 f x 在 0,e 上单调递增,在 e, 上单调递减,故
x2
f 3 f 4 f 5 .
又 f 2 f 4 ,所以 f 3 f 2 f 5 ,即 f b f a f c .
因为a,b,c 0,e ,所以c a b ,故选 A.
二、多选题(本题共 4小题,每小题 5分,共 20分。在每小题给出的选项中,有多项符合题目要求。
全部选对的得 5分,部分选对的得 2分,有选错的得 0分。)
题目 9 10 11 12
答案 ACD CD BD ABD
第 12题详细解答如下:
对于 A,由于平面 A1BC1 / / 平面 AD1C ,所以 A1P / / 平面 AD1C ,所以 A正确;
5
对于 B,当B1P BC1时, A1P 与平面BCC1B1所成角的正切值最大,最大值是 ,所以 B正确;
2
对于 C,将 A1C1B 沿BC1翻折与 BCC1在同一个平面,且点 A1,C 在直线BC1的异侧,此时
2 170 170
cos AC C ,则 AC ,所以 A1P PC 的最小值为 ,所以 C不正确; 1 1 1
10 5 5
对于 D,由于 AD 平面DCC1D1 ,所以交线为以D为圆心,半径为 1 的四分之一圆周,所以交线长为
2022届广东省四校第一次联考数学参考答案 第 1 页 共 8 页
,所以 D正确.故选:ABD.
2
三、填空题(本题共 4小题,每小题 5分,共 20分。其中第 16题第一空 2分,第二空 3分。)
题目 13 14 15 16
4001
4 5 y x 1
答案 , 2 20 4000
5 3
(此空 2分) (此空 3分)
第 15题详细解答如下:
设 BC 中点为T , ABC的外心为O1, PBC 的外心为O2 ,过点O1作平面 ABC 的垂线,过点O2 作
平面PBC 的垂线,两条垂线的交点O即为三棱锥P ABC 外接球的球心.
因为 ABC和 PBC 都是边长为2 3的正三角形,可得PT AT 3.
PA 3 2 2又 ,所以 AT PT 2 AP2 ,所以PT AT .
又因为BC AT ,PT BC T ,所以 AT 平面PBC .
1 1
因为 AT 平面 ABC ,所以平面PBC 平面 ABC ,且TO1 AT 1,TO2 PT 1
3 3
所以四边形OO1TO
2 2
2 是边长为 1的正方形,所以外接球半径R OP OO2 O2P 1 4 5 ,
故外接球的表面积为 S 4 R2 20 .
第 16题详细解答如下:
1
由题意,得 f x ,则 f 1 1,故所求切线方程为 y x 1;
x
因为 1 与 1 之间的距离比较小,因此在切点附近用切线代替曲线,近似计算,得
4000 e e4000
1 1 1 1 1
4000 1 4001f e ln e
4000 e4000 1,即e4000 ln e4000 1 1 .
4000 4000
2022届广东省四校第一次联考数学参考答案 第 2 页 共 8 页
四、解答题(本题共 6小题,共 70分。解答应写出文字说明、证明过程或演算步骤。)
17.(本小题满分 10分)
选择条件①.
因为2acos A ccos B bcosC ,
根据正弦定理,得2sin Acos A sinCcosB sin BcosC ,…………………………1分
即2sin Acos A sin B C sin A sin A,…………………………2分
1
因为 A 0, ,所以sin A 0 ,所以cos A ,所以 A .…………………………4分
2 3
1 1 3 3
由 S ABC bcsin A b 2sin ,…………………………6分
2 2 3 2
解得b 3 1.…………………………7分
2 1
根据余弦定理,得a b2 c2 2bccos A 4 2 3 4 2 3 1 2 6,………………9分
2
所以a 6 .…………………………10分
选择条件②.
因为asin B bsin A ,根据正弦定理,得sin Asin B sin Bsin A ……………1分
3 3
1 3
由 B 0, ,得sin B 0 ,所以sin A sin A sin A cos A,……………………2分
3 2 2
sin A
则 tan A 3 .…………………………3分
cos A
又 A 0, ,所以 A .…………………………4分
3
1 1 3 3
由 S ABC bcsin A b 2sin ,…………………………6分
2 2 3 2
解得b 3 1.…………………………7分
2 2 2 1
根据余弦定理,得a b c 2bccos A 4 2 3 4 2 3 1 2 6,………………9分
2
所以a 6 .…………………………10分
2022届广东省四校第一次联考数学参考答案 第 3 页 共 8 页
18.(本小题满分 12分)
(1)由女志愿者考核成绩的频率分布表可知被抽取的女志愿者的人数为2 0.050 40 .
因为0.050 0.325 m 0.100 0.075 1,所以m 0.45.…………………………1分
所以a 40 0.100 4,b 40 0.075 3.…………………………3分
因为被抽取的志愿者人数是 80,所以被抽取的男志愿者人数是80 40 40 .
由男志愿者考核成绩频率分布直方图可知男志愿者这次培训考核等级为优秀的频率为
0.010 0.015 5 0.125,则这次培训考核等级为优秀的男志愿者人数为40 0.125 5.…4分
(2)由题可知,这次培训考核等级为优秀的女志愿者人数为4 3 7 ,故样本中考核等级为优秀的志
愿者人数为5 7 12 ,则 X 的可能取值为 0,1,2,3. …………………………6分
C3 35 7
P X 0 7 …………………………7分
C312 220 44
C15C
2
7 105 21P X 1 …………………………8分
C312 220 44
C2 15 C7 70 7P X 2 …………………………9分
C312 220 22
C3 10 1
P X 3 5 …………………………10分
C312 220 22
所以 X 的分布列为
X 0 1 2 3
7 21 7 1
P
44 44 22 22
…………………………11分
7 21 7 1 5
故 EX 0 1 2 3 .…………………………12分
44 44 22 22 4
19.(本小题满分 12分)
(1)因为3an 2Sn 2 n N ,所以,当n 2时,3an 1 2Sn 1 2 ,
a
所以3 an an 1 2 Sn Sn 1 0 ,所以3 an an 1 2an 0,即
n 3 n 2 .………2分
an 1
当 n 1时,3a1 2S1 2,
又 S1 a1,所以a1 2,…………………………3分
2022届广东省四校第一次联考数学参考答案 第 4 页 共 8 页
所以数列 an 是以 2为首项,3为公比的等比数列.
n 1
所以an 2 3 .…………………………4分
设等差数列 bn 的公差为d ,d 0 .
2
因为b 1,b4是b 与b 的等比中项,所以b4 b2b8 ,…………………………5分 1 2 8
2
即 1 3d 1 d 1 7d ,解得d 1或d 0 (舍去).…………………………6分
所以bn 1 n 1 1 n.…………………………7分
n 1
2 3 ,n为偶数
(2)由题意,得 cn .…………………………8分
n 2,n为奇数
所以T2n c1 c3 c2n 1 c2 c4 c2n …………………………9分
3 5 2n 1 2 3
1 33 32n 1 …………………………10分
3 2n 1 n 3 1 9n
2 …………………………11分
2 1 9
3 9n 1
n2 2n …………………………12分
4
20.(本小题满分 12分)
5
(1)在 BCD中,CD BC 7 ,cos DCB ,
7
5
由余弦定理,得BD CD2 BC2 2CD BC cos DCB 7 7 2 7 7 2.…1分
7
连结BE ,因为BD DE 2, EDB 60 ,所以BE 2.…………………………2分
又因为EP 3 ,故在 PBE中, EP2 BE2 PB2 ,所以PE BE .…………………………3分
同理可证PE DE .…………………………4分
因为BE DE E , BE , DE 平面 ABDE ,所以PE 平面 ABDE .…………………………5分
2022届广东省四校第一次联考数学参考答案 第 5 页 共 8 页
(2)以E 为坐标原点,EA , EP所在直线为 x 轴,z 轴建立如图所示
空间直角坐标系E xyz ,
则 P 0,0, 3 ,B 1, 3,0 , D 1, 3,0 .………………………6分
所以PB 1, 3, 3 , BD 2,0,0 …………………………7分
n PB x 3y 3z 0
设平面PBD的一个法向量为n x, y, z ,则 .……………………8分
n BD 2x 0
令 y 1,则 z 1, x 0 ,故n 0,1,1 .…………………………9分
又平面PAE 的一个法向量为m 0,1,0 ,…………………………10分
n m 1 2
所以 cos n,m ,…………………………11分
n m 2 2
故平面PAE 与平面PBD所成锐二面角的大小为 .…………………………12分
4
注:使用几何法求解第(2)问同样给分.
21.(本小题满分 12分)
(1)因为椭圆C 上任意一点P 到焦点距离的最大值是最小值的3倍,
所以a c 3 a c ,即a 2c .…………………………1分
2b2
因为过焦点且垂直于长轴的弦长为3 ,所以 3.…………………………2分
a
又a2 b2 c2 ,联立方程组,解得a 2,b 3,c 1.…………………………3分
x2 y2
故椭圆C 的标准方程为 1.…………………………4分
4 3
1
(2)设 ABF1的内切圆半径为 r ,则 S ABF AF1 AB BF r . 1 12
又因为 AF1 AB BF1 8 ,所以 S ABF 4r .…………………………5分 1
要使得 ABF1的内切圆面积最大,只需 S ABF 的值最大. 1
由题意,得直线 l 斜率不为0 ,故设 A x1, y1 , B x2 , y2 ,直线 l : x my 1.
2022届广东省四校第一次联考数学参考答案 第 6 页 共 8 页
x2 y2
1
由 4 3 ,得 3m2 4 y2 6my 9 0.…………………………6分
x my 1
6m
y1 y2 3m2 4
所以 .…………………………7分
9y1y2 2
3m 4
1 2
所以 S ABF F1F2 y1 y2 y1 y2 4y1 1y2 2
36m2 36 12 m2 1
…………………………8分
2 2
3m2 4 3m 4 3 m
2 1 1
2 12t 12
设 t m 1 1,则 S ABF .…………………………9分 1 3t2 1 1
3t
t
1 1
设 f t 3t , t 1,则 f t 3 0 ,故 f2 t 在 1, 上单调递增.…………………10分 t t
3
所以当 t 1,即m 0时, S ABF 的最大值为3 ,此时 r .…………………………11分 1 4
9
所以 ABF1的内切圆面积最大值为 .…………………………12分
16
22.(本小题满分 12分)
(1)由题意,得 f x e ax ax e ax e ax 1 ax …………………………1分
①当a 0时, f x 1 0,则 f x 在 , 上单调递增.…………………………2分
1
②当a 0时,由 f x 0,得 x .
a
1 1
若 a 0 ,则 x , , f x 0; x , , f x 0;…………………………3分
a a
1 1
若 a 0则 x , , f x 0; x , , f x 0.…………………………4分
a a
综上,得
当 a 0时, f x 在 , 上单调递增;
1 1
当 a 0时, f x 在 , 上单调递减,在 , 上单调递增;
a a
2022届广东省四校第一次联考数学参考答案 第 7 页 共 8 页
1 1
当 a 0时, f x 在 , 上单调递增,在 , 上单调递减.…………………………5分
a a
1 1
(2)由(1)知,当a 0时, f x 在 , 上单调递增,在 , 上单调递减.
a a
1 1 1
且当 x 时, f x 0 , f x 有极大值 f .
a a ae
1 1
因为a 0,函数 y f x a 有两个零点 x 21, x2 ,所以a ,即a .……………………6分
ae e
1 2 2
不妨设 x1 x2 ,则0 x1 x2 .先证 x1 x2 ,即证 x1 x2 .…………………………7分
a a a
1 2 1 1 2
因为 x1 , x2 ,且 f x 在 , 上单调递增,所以即证 f x1 f x . 2
a a a a a
2
又 f x1 f x2 ,所以即证 f x f x . 2 2
a
2 2
F x f x f x x e ax x e 2 ax
1
令 , x , .…………………………8分
a a a
2
则 F x e ax 1 ax e 2 ax 1 a x 1 ax e
ax e 2 ax …………………………9分
a
1
x , , ax ax 2 ,1 ax 0,故F x 1 ax e
ax e 2 ax 0
a
2 1
所以函数F x f x f x 在 , 上单调递增.
a a
1
所以F x F 0 .…………………………10分
a
1 2 2
因为 x2 ,所以 f x2 f x2 ,即 x1 x2 .…………………………11分
a a a
1 2
又 a2 ,即 2 e ,
e a
所以 x1 x2 2 e .…………………………12分
2022届广东省四校第一次联考数学参考答案 第 8 页 共 8 页
同课章节目录
