2021-2022学年人教版数学七年级下册 5.1.1相交线 课件(共23张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册 5.1.1相交线 课件(共23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
5.1.1相交线
A
B
C
D
O
直线AB、CD相交于点O
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点.
1
2
A
C
D
O
3
4
B
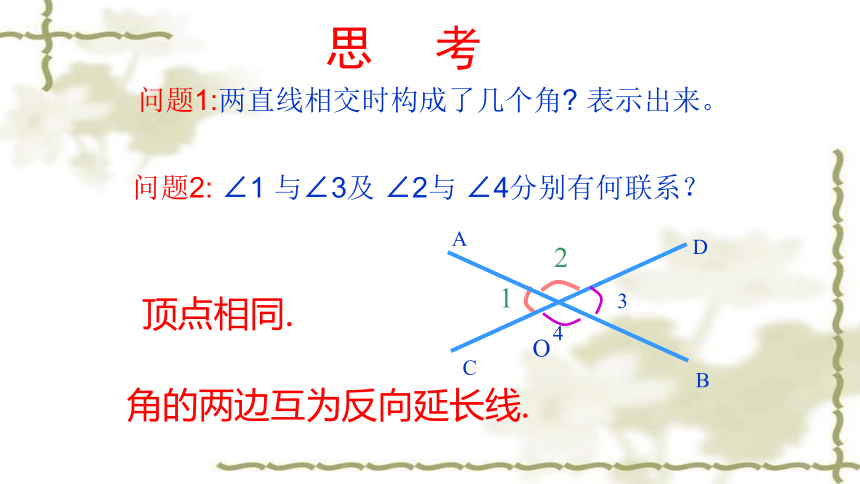
思 考
问题1:两直线相交时构成了几个角 表示出来。
问题2: ∠1 与∠3及 ∠2与 ∠4分别有何联系?
顶点相同.
角的两边互为反向延长线.
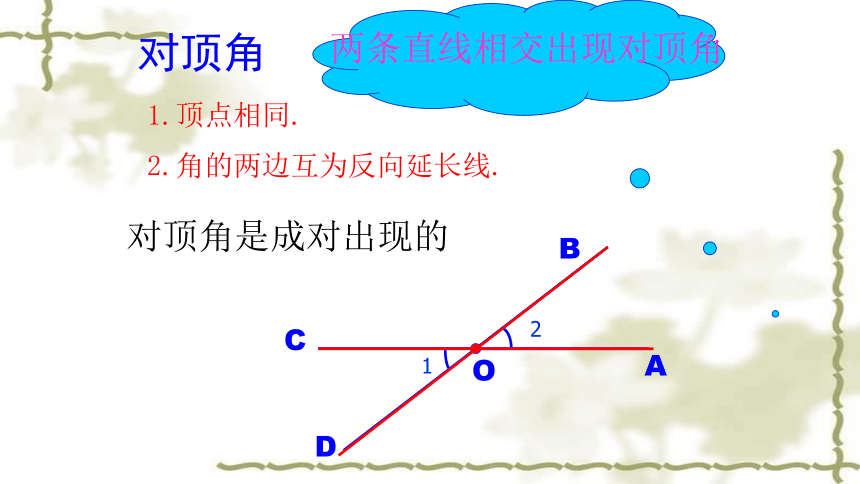
对顶角
1.顶点相同.
2.角的两边互为反向延长线.
B
A
O
C
D
1
2
两条直线相交出现对顶角
对顶角是成对出现的
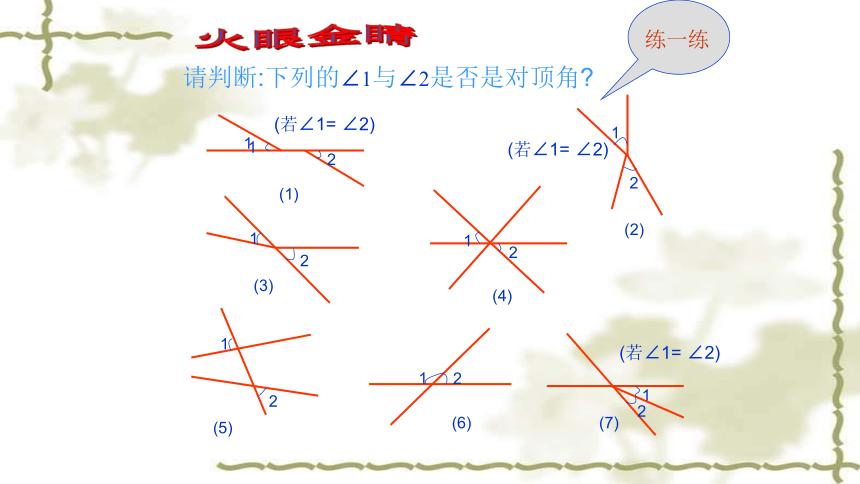
请判断:下列的∠1与∠2是否是对顶角
1
2
1
2
1
2
1
2
1
2
1
2
1
1
2
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(若∠1= ∠2)
(若∠1= ∠2)
(若∠1= ∠2)
练一练
火眼金睛
1
2
A
C
D
O
3
4
B
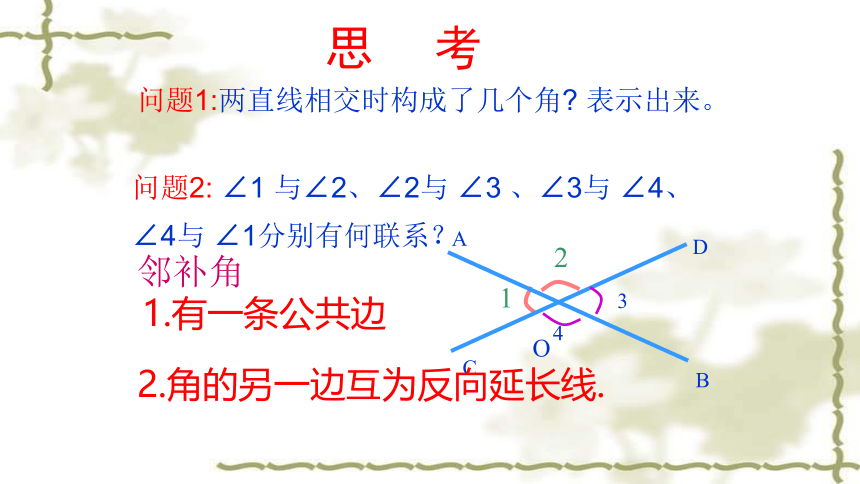
思 考
问题1:两直线相交时构成了几个角 表示出来。
问题2: ∠1 与∠2、∠2与 ∠3 、∠3与 ∠4、 ∠4与 ∠1分别有何联系?
1.有一条公共边
2.角的另一边互为反向延长线.
邻补角
邻补角与补角的区别与联系
1.邻补角与补角都是针对两个角而言的,而且数量关系都是两角之和为180°
2.互为邻补角的两个角一定互补,但是互为补角的两个角不一定是邻补角即:互补的两个角只注重数量关系而不谈位置,而互为邻补角的两个角既要满足数量关系又要满足位置关系。
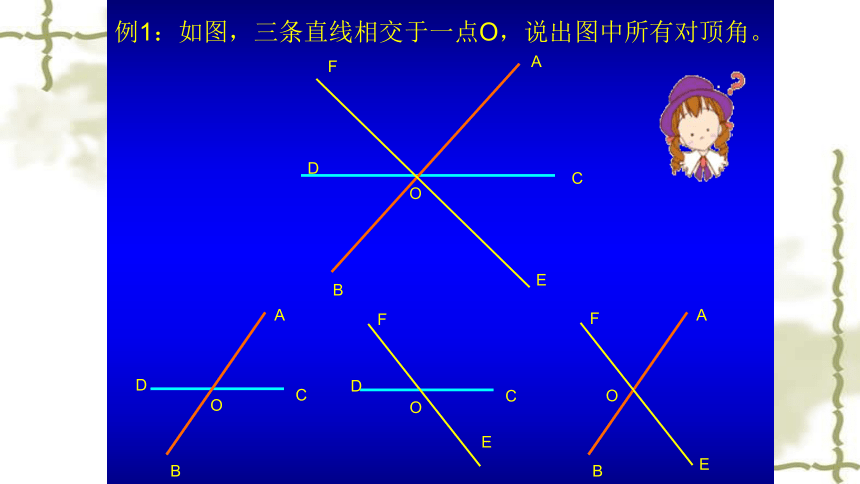
例1:如图,三条直线相交于一点O,说出图中所有对顶角。
A
B
C
D
E
F
O
E
A
B
C
D
O
C
D
F
O
A
B
E
F
O
做 一 做
图中共有几组对顶角?
A
B
C
2
1
2
1
用剪刀剪东西时, 1和 2同时
增大又同时缩小,你能猜出 1
和 2的大小关系吗?
猜 一 猜
在下图中,如果 1=42°,
那么 2等于多少度?
你能说明理由吗?
1
2
O
对顶角相等
说一说
例2、如图,已知直线AD和BE相交于点O, ∠ DOE与∠ COE互余, ∠ COE =500,求∠ AOB和∠ BOD的度数。
A
O
D
B
E
C
解:∵∠DOE与∠ COE互余(已知)
∴ ∠DOE+∠ COE =900 (互余的意义)
∴ ∠DOE= 900 -∠ COE= 900 -500=400
又∵ ∠AOB与∠DOE是对顶角(已知)
∴ ∠AOB=∠DOE =40°(对顶角相等)
∵ ∠BOD 与∠AOB互为邻补角
∴ ∠BOD =180°-40°=140°
变式练习
已知:直线a,b相交, 1=35度,求 2, 3, 4的度数。
a
b
4
3
2
1
评:此题可借助方程来求解,几何中计算角的大小或线段长度等问题常借助代数的方程来解决。
变式:把 1=35度改为
2是 1的4倍,求 2,
3, 4的度数。
做一做
1、如图,三条直线l1,l2,l3交于点O,求 2+ 4+ 6
等于多少?
l1
l2
l3
o
1
3
2
6
5
4
(1)对顶角相等 ( )
(2)相等的角是对顶角( )
(3)若两个角不相等,则这两个角一定不是对顶
角。( )
判断
(4)若这两个角不是对顶角,则这两个角不相等。( )
(5)有公共顶点,并且相等的角是对顶角( )
(6)两条直线相交,有公共顶点的角是对顶角( )
Y
N
N
N
N
Y
已知:如图, ∠ 1=60度,OE平分 ∠ AOC,
求 ∠ EOC和 ∠ BOC的度数。
求一求
1
A
B
C
D
E
O
想一想
观察图,寻找对顶角(不含平角)
(1)
(2)
(3)
若有8条直线相交于一点,则可形
成 对对顶角?
合作交流
若有n条直线相交于一点呢?
1、若∠1与∠2是对顶角,∠1=100,则∠2=______0;
若 ∠3与∠4是邻补角,则∠3+∠4 =______0
180
180
2、若∠1与∠2为对顶角,∠1与∠3互补,则 ∠2+∠3= 0
10
课堂练习:
3.如图,AB、CD、EF是经过点O的三条直线,说出:∠AOC,∠FOB,∠DOF,∠AOD,∠EOB 的对顶角分别是 ,∠AOF 的邻补角是 、
∠BOD,∠AOE,∠COE,∠BOC,∠AOF
∠BOF 和∠AOE
4、如图2,直线AB、CD
相交于O,OE是射线。则
∠3的对顶角是_____________,
∠3的邻补角是_____________
∠1的对顶角是_____________,
∠1的邻补角是_____________,
∠2的邻补角是_____________。
图2
∠AOD
∠1
∠BOD
∠3
∠COE
5.直线AB,CD相交于点O,OE平分
∠BOD且∠AOC=∠BOC-30° ,
求∠AOE
角的名称
邻补角
对顶角
位置关系
2、有一条公共边
3、另一边互为反向延长线
1、有公共顶点
1、有公共顶点
2、没有公共边
3、两边互为反向延长线
性质
邻补角互补
对顶角相等
相同点
都有一个公共顶点,它们都是成对出现的
不同点
对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个
知识回顾:
再见
努力 努力 再努力!
5.1.1相交线
A
B
C
D
O
直线AB、CD相交于点O
如果两条直线只有一个公共点,就说这两条直线相交.
该公共点叫做两直线的交点.
1
2
A
C
D
O
3
4
B
思 考
问题1:两直线相交时构成了几个角 表示出来。
问题2: ∠1 与∠3及 ∠2与 ∠4分别有何联系?
顶点相同.
角的两边互为反向延长线.
对顶角
1.顶点相同.
2.角的两边互为反向延长线.
B
A
O
C
D
1
2
两条直线相交出现对顶角
对顶角是成对出现的
请判断:下列的∠1与∠2是否是对顶角
1
2
1
2
1
2
1
2
1
2
1
2
1
1
2
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(若∠1= ∠2)
(若∠1= ∠2)
(若∠1= ∠2)
练一练
火眼金睛
1
2
A
C
D
O
3
4
B
思 考
问题1:两直线相交时构成了几个角 表示出来。
问题2: ∠1 与∠2、∠2与 ∠3 、∠3与 ∠4、 ∠4与 ∠1分别有何联系?
1.有一条公共边
2.角的另一边互为反向延长线.
邻补角
邻补角与补角的区别与联系
1.邻补角与补角都是针对两个角而言的,而且数量关系都是两角之和为180°
2.互为邻补角的两个角一定互补,但是互为补角的两个角不一定是邻补角即:互补的两个角只注重数量关系而不谈位置,而互为邻补角的两个角既要满足数量关系又要满足位置关系。
例1:如图,三条直线相交于一点O,说出图中所有对顶角。
A
B
C
D
E
F
O
E
A
B
C
D
O
C
D
F
O
A
B
E
F
O
做 一 做
图中共有几组对顶角?
A
B
C
2
1
2
1
用剪刀剪东西时, 1和 2同时
增大又同时缩小,你能猜出 1
和 2的大小关系吗?
猜 一 猜
在下图中,如果 1=42°,
那么 2等于多少度?
你能说明理由吗?
1
2
O
对顶角相等
说一说
例2、如图,已知直线AD和BE相交于点O, ∠ DOE与∠ COE互余, ∠ COE =500,求∠ AOB和∠ BOD的度数。
A
O
D
B
E
C
解:∵∠DOE与∠ COE互余(已知)
∴ ∠DOE+∠ COE =900 (互余的意义)
∴ ∠DOE= 900 -∠ COE= 900 -500=400
又∵ ∠AOB与∠DOE是对顶角(已知)
∴ ∠AOB=∠DOE =40°(对顶角相等)
∵ ∠BOD 与∠AOB互为邻补角
∴ ∠BOD =180°-40°=140°
变式练习
已知:直线a,b相交, 1=35度,求 2, 3, 4的度数。
a
b
4
3
2
1
评:此题可借助方程来求解,几何中计算角的大小或线段长度等问题常借助代数的方程来解决。
变式:把 1=35度改为
2是 1的4倍,求 2,
3, 4的度数。
做一做
1、如图,三条直线l1,l2,l3交于点O,求 2+ 4+ 6
等于多少?
l1
l2
l3
o
1
3
2
6
5
4
(1)对顶角相等 ( )
(2)相等的角是对顶角( )
(3)若两个角不相等,则这两个角一定不是对顶
角。( )
判断
(4)若这两个角不是对顶角,则这两个角不相等。( )
(5)有公共顶点,并且相等的角是对顶角( )
(6)两条直线相交,有公共顶点的角是对顶角( )
Y
N
N
N
N
Y
已知:如图, ∠ 1=60度,OE平分 ∠ AOC,
求 ∠ EOC和 ∠ BOC的度数。
求一求
1
A
B
C
D
E
O
想一想
观察图,寻找对顶角(不含平角)
(1)
(2)
(3)
若有8条直线相交于一点,则可形
成 对对顶角?
合作交流
若有n条直线相交于一点呢?
1、若∠1与∠2是对顶角,∠1=100,则∠2=______0;
若 ∠3与∠4是邻补角,则∠3+∠4 =______0
180
180
2、若∠1与∠2为对顶角,∠1与∠3互补,则 ∠2+∠3= 0
10
课堂练习:
3.如图,AB、CD、EF是经过点O的三条直线,说出:∠AOC,∠FOB,∠DOF,∠AOD,∠EOB 的对顶角分别是 ,∠AOF 的邻补角是 、
∠BOD,∠AOE,∠COE,∠BOC,∠AOF
∠BOF 和∠AOE
4、如图2,直线AB、CD
相交于O,OE是射线。则
∠3的对顶角是_____________,
∠3的邻补角是_____________
∠1的对顶角是_____________,
∠1的邻补角是_____________,
∠2的邻补角是_____________。
图2
∠AOD
∠1
∠BOD
∠3
∠COE
5.直线AB,CD相交于点O,OE平分
∠BOD且∠AOC=∠BOC-30° ,
求∠AOE
角的名称
邻补角
对顶角
位置关系
2、有一条公共边
3、另一边互为反向延长线
1、有公共顶点
1、有公共顶点
2、没有公共边
3、两边互为反向延长线
性质
邻补角互补
对顶角相等
相同点
都有一个公共顶点,它们都是成对出现的
不同点
对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个
知识回顾:
再见
努力 努力 再努力!
