人教版八年级数学上册第14.2.1平方差公式 同步教学课件(共27张PPT)
文档属性
| 名称 | 人教版八年级数学上册第14.2.1平方差公式 同步教学课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 993.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 19:46:01 | ||
图片预览







文档简介
(共27张PPT)
平方差公式
2021/12/28
阅读小故事,并回答问题:
小明和小兰分别负责两块区域的值日工作.小明负责一块边长为a米的正方形空地,小兰则负责一块长方形空地,长为正方形空地边长加5米,宽度是正方形空地边长减5米.有一天,小明对小兰说:“咱们换一下值日的区域吧,反正这两块地大小都一样.”你觉得小明说的对吗?为什么?
a米
a米
(a-5)米
(a+5)米
2021/12/28
阅读小故事,并回答问题:
a米
a米
(a-5)米
(a+5)米
答:小明说的不对,长方形面积比正方形面积少了25平方米.
2021/12/28
探究新知
计算下面多项式的积,你发现什么规律?
这两个数的平方差
两数的和与这两数
的差的乘积
探究新知
计算下面多项式的积,你发现什么规律?
两个数的和与这两个数差的积,等于这两个数的平方差.
文字描述:
符号语言:
(a+b)(a-b)=
a2-b2
归纳:
两个数的和与这两个数差的积,等于这两个数的平方差.
代数推导:
文字描述:
结构特点:
左边:a符号相同,b符号相反.
右边:符号相同项a的平方减去符号相反项b的平方.
平方差公式
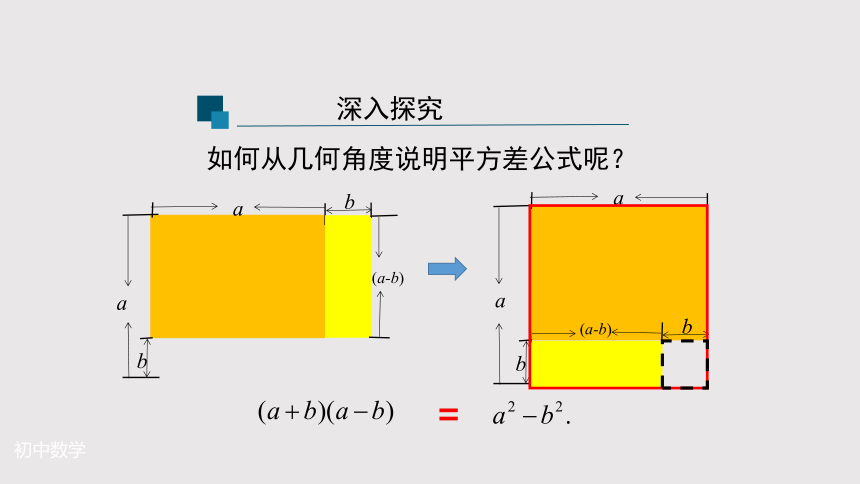
深入探究
如何从几何角度说明平方差公式呢?
a
b
a
b
(a-b)
a
a
b
(a-b)
b
=
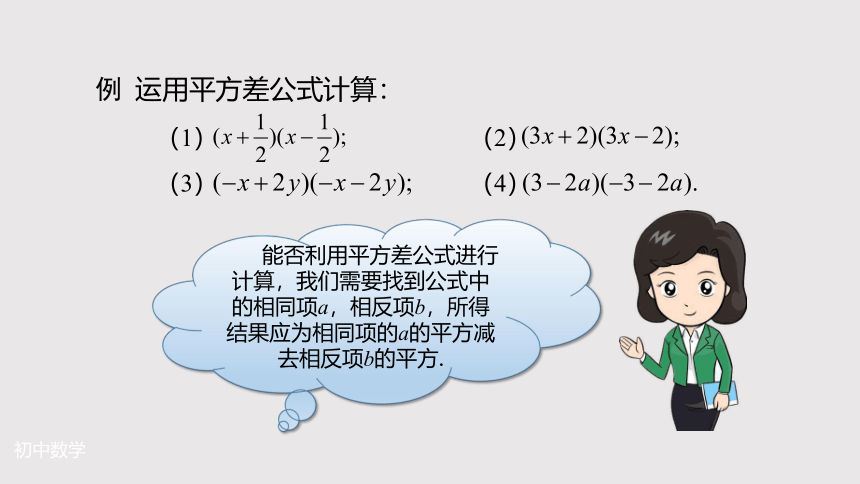
例 运用平方差公式计算:
(1) (2)
(3) (4)
能否利用平方差公式进行计算,我们需要找到公式中的相同项a,相反项b,所得结果应为相同项的a的平方减去相反项b的平方.
例 运用平方差公式计算:
(1) (2)
(3) (4)
分析:
(1)
.
解:
(1)
.
例 运用平方差公式计算:
(1) (2)
(3) (4)
想一想:(2)中相同项,相反项分别是什么?
例 运用平方差公式计算:
(1) (2)
(3) (4)
分析:
(2)
.
注意此处为3x整体的平方,为9x2.
解:
(2)
.
例 运用平方差公式计算:
(1) (2)
(3) (4)
你能说出(3)和(4)中相同项,相反项,然后再利用公式计算出结果吗?
例 运用平方差公式计算:
(1) (2)
(3) (4)
解:
(3)
(4)
.
.
练习
下列各式中,不能运用平方差公式的是( )
分析:
若能利用平方差公式,则需要在式子中找到相同项a,相反项b,若两项均为相同项,或者均为相反项,则无法利用公式计算.
C
例
计算:
(1) ; (2) ;
(3) ; (4) .
例
计算:
(1) ; (2) ;
.
分析:
(1)中只有前半部分符合公式条件,可以利用平方差公式简便运算,其余的运算仍按照乘法法则进行.
解:
例
计算:
(1) ; (2) ;
分析:
解:
(2)是两个数字相乘,通过观察发现这两个数字很有特点,一个是102=100+2,98=100-2,可以利用平方差公式进行简便运算.
(3) ; (4) .
例
计算:
分析:
解:
(3)xn可以看成公式中的a,4可以看成公式中的b,根据平方差公式,结果为(xn)2-42.
(3) ; (4) .
例
计算:
分析:
解:
(4)需要先把前两项利用平方差公式计算出来,然后利用结果二次利用平方差公式,从而得到最终结果.
(1) (2)
(3) (4)
例
在括号中填入适当的整式
分析:
观察此题的结果,是两数的平方差,再对比左侧已知的因式,分析出谁是相同项,谁是相反项.
a
-b
-n
-m
-1
+3x
a2
-b2
例
已知:x2-y2=12, x-y=2 , 则 ________.
分析:
x2-y2=12
x-y=2
利用平方差公式
(x+y)(x-y)=x2-y2
x+y=6,
x-y=2
解二元一次方程组
x,y的值
x
y
的值
例
已知:x2-y2=12, x-y=2 , 则 ________.
解:
由(x+y)(x-y)=x2-y2 ,
且已知x2-y2=12, x-y=2 ,
得2(x+y)=12,
又因为 x+y=6
x-y=2 ,
所以
所以x+y=6.
解得 x=4
y=2.
2
想一想:我们今天学习了哪些知识?
归纳总结
1.平方差公式:
文字描述:“两个数的和与这两个数差的积,等于这
两个数的平方差”.
.
归纳总结
2.平方差公式推导:
(1)代数推导:
(2)几何推导:
计算:
拓展提升
解:原式
.
.
1.下面各式计算的对不对?如果不对,怎样改正?
2.下运用平方差公式计算:
课后作业
;
;
;
;
.
.
平方差公式
2021/12/28
阅读小故事,并回答问题:
小明和小兰分别负责两块区域的值日工作.小明负责一块边长为a米的正方形空地,小兰则负责一块长方形空地,长为正方形空地边长加5米,宽度是正方形空地边长减5米.有一天,小明对小兰说:“咱们换一下值日的区域吧,反正这两块地大小都一样.”你觉得小明说的对吗?为什么?
a米
a米
(a-5)米
(a+5)米
2021/12/28
阅读小故事,并回答问题:
a米
a米
(a-5)米
(a+5)米
答:小明说的不对,长方形面积比正方形面积少了25平方米.
2021/12/28
探究新知
计算下面多项式的积,你发现什么规律?
这两个数的平方差
两数的和与这两数
的差的乘积
探究新知
计算下面多项式的积,你发现什么规律?
两个数的和与这两个数差的积,等于这两个数的平方差.
文字描述:
符号语言:
(a+b)(a-b)=
a2-b2
归纳:
两个数的和与这两个数差的积,等于这两个数的平方差.
代数推导:
文字描述:
结构特点:
左边:a符号相同,b符号相反.
右边:符号相同项a的平方减去符号相反项b的平方.
平方差公式
深入探究
如何从几何角度说明平方差公式呢?
a
b
a
b
(a-b)
a
a
b
(a-b)
b
=
例 运用平方差公式计算:
(1) (2)
(3) (4)
能否利用平方差公式进行计算,我们需要找到公式中的相同项a,相反项b,所得结果应为相同项的a的平方减去相反项b的平方.
例 运用平方差公式计算:
(1) (2)
(3) (4)
分析:
(1)
.
解:
(1)
.
例 运用平方差公式计算:
(1) (2)
(3) (4)
想一想:(2)中相同项,相反项分别是什么?
例 运用平方差公式计算:
(1) (2)
(3) (4)
分析:
(2)
.
注意此处为3x整体的平方,为9x2.
解:
(2)
.
例 运用平方差公式计算:
(1) (2)
(3) (4)
你能说出(3)和(4)中相同项,相反项,然后再利用公式计算出结果吗?
例 运用平方差公式计算:
(1) (2)
(3) (4)
解:
(3)
(4)
.
.
练习
下列各式中,不能运用平方差公式的是( )
分析:
若能利用平方差公式,则需要在式子中找到相同项a,相反项b,若两项均为相同项,或者均为相反项,则无法利用公式计算.
C
例
计算:
(1) ; (2) ;
(3) ; (4) .
例
计算:
(1) ; (2) ;
.
分析:
(1)中只有前半部分符合公式条件,可以利用平方差公式简便运算,其余的运算仍按照乘法法则进行.
解:
例
计算:
(1) ; (2) ;
分析:
解:
(2)是两个数字相乘,通过观察发现这两个数字很有特点,一个是102=100+2,98=100-2,可以利用平方差公式进行简便运算.
(3) ; (4) .
例
计算:
分析:
解:
(3)xn可以看成公式中的a,4可以看成公式中的b,根据平方差公式,结果为(xn)2-42.
(3) ; (4) .
例
计算:
分析:
解:
(4)需要先把前两项利用平方差公式计算出来,然后利用结果二次利用平方差公式,从而得到最终结果.
(1) (2)
(3) (4)
例
在括号中填入适当的整式
分析:
观察此题的结果,是两数的平方差,再对比左侧已知的因式,分析出谁是相同项,谁是相反项.
a
-b
-n
-m
-1
+3x
a2
-b2
例
已知:x2-y2=12, x-y=2 , 则 ________.
分析:
x2-y2=12
x-y=2
利用平方差公式
(x+y)(x-y)=x2-y2
x+y=6,
x-y=2
解二元一次方程组
x,y的值
x
y
的值
例
已知:x2-y2=12, x-y=2 , 则 ________.
解:
由(x+y)(x-y)=x2-y2 ,
且已知x2-y2=12, x-y=2 ,
得2(x+y)=12,
又因为 x+y=6
x-y=2 ,
所以
所以x+y=6.
解得 x=4
y=2.
2
想一想:我们今天学习了哪些知识?
归纳总结
1.平方差公式:
文字描述:“两个数的和与这两个数差的积,等于这
两个数的平方差”.
.
归纳总结
2.平方差公式推导:
(1)代数推导:
(2)几何推导:
计算:
拓展提升
解:原式
.
.
1.下面各式计算的对不对?如果不对,怎样改正?
2.下运用平方差公式计算:
课后作业
;
;
;
;
.
.
