华东师大版数学八年级上册 12.5 用平方差进行因式分解课件(共16张PPT)
文档属性
| 名称 | 华东师大版数学八年级上册 12.5 用平方差进行因式分解课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1018.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 21:04:47 | ||
图片预览






文档简介
(共14张PPT)
2、判断下列变形过程,哪些是因式分解?
(1) (x+2)(x-2)=x2- 4 ( )
(2) x2- 4+3x=(x+2)(x-2)+3x ( )
(3) 7m-7n-7=7(m-n-1) ( )
(4) 4x2- 9 =(2x+3)(2x- 3 ) ( )
×
×
√
√
1、什么叫多项式的因式分解
把一个多项式化为几个整式乘积的形式,叫做多项式的因式分解
一、复习引入
a米
b米
b米
a米
(a-b)
二、探究新知
如图,在边长为a米的正方形上剪掉一个边长为b米的小正方形,将剩余部分拼成一个长方形,根据此图形变换,你能得到什么公式?
a2- b2=(a+b)(a-b)
二、探索新知
用平方差公式进行因式分解
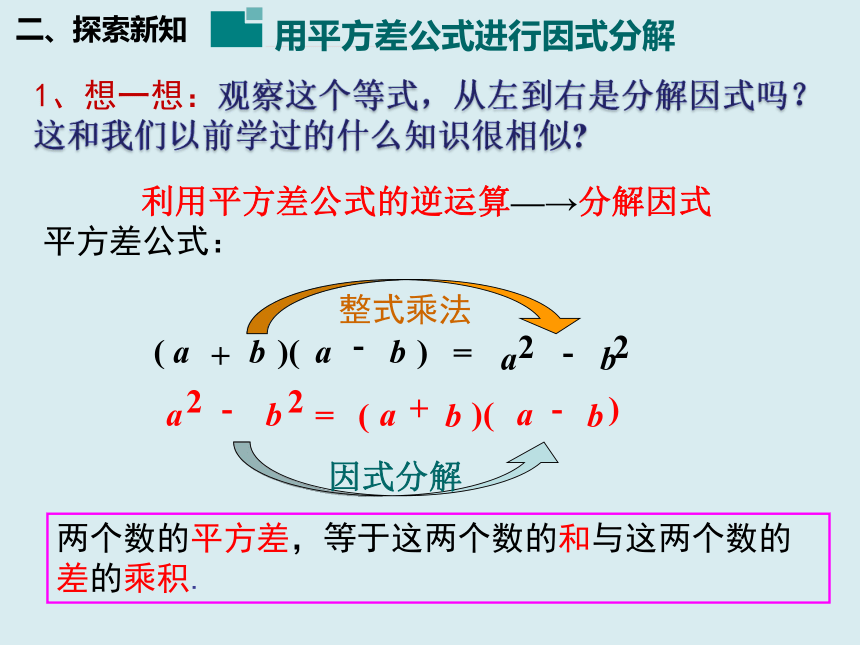
1、想一想:观察这个等式,从左到右是分解因式吗?
这和我们以前学过的什么知识很相似
利用平方差公式的逆运算—→分解因式
)
)(
(
b
a
b
a
-
+
=
2
2
b
a
-
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
整式乘法
因式分解
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
平方差公式:
a2 b2= (a+b)(a b)
□2-△2=(□+△)(□-△)
☆2-○2=(☆+○)(☆-○)
说说平方差公式的特点
两数的和与差的积
两个数的平方差;只有两项
形象地表示为
①左边
②右边
相同项
相反项
2、议一议
√
√
×
×
3、辨一辨
下列多项式能否用平方差公式来分解因式,为什么?
√
√
★符合平方差的形式的多项式才能用平方差公式进行因式分解,即能写成: ( )2-( )2的形式.
(1)x2+y2
(2)x2-y2
(3)-x2-y2
-(x2+y2)
y2-x2
(4)-x2+y2
(5)x2-25y2
(x+5y)(x-5y)
(6)m2-1
(m+1)(m-1)
你会填下列各空吗?
(1)4x2=( )2 25m2=( )2
(2) a4=( )2 0.49b2=( )2
(3) x4y2-4
(4) x2-0.01y2
9
49
=( )2-( )2
=( )2-( )2
x2y
2
0.1y
3
7
x
公式:(ab)n=anbn
4、练一练:
2x
5m
a2
0.7b
把下列各式分解因式
(1) 1-25x2
解: 1-25x2
1、把两项写成平方的形式,找出a和b
2、利用a2-b2=(a-b)(a+b)
分解因式
=12-(5x)2
=(1+5x)(1-5x)
(2)4x - m n
=(2x)2-(mn)2
=(2x+mn)(2x-mn)
三、典例精析
把下列各式分解因式
法一:
原式=
变式:-25x2
+1
+1
-25x2
(前后两项利用加法交换律交换位置)
=12-(5x)2
=(1+5x)(1-5x)
法二:
原式=-( 25x2 )
(把各项先提出一个“负号”)
=-[(5x)2-12]
=-(5x+1)(5x-1)
-1
例3:分解因式: (1) x5-x3
解:(1)
x5-x3 =
x3
(x2 –1)
= x3 (x+1)(x-1)
结论:
1、若有公因式,要先提公因式,再考虑 平方差公式.
2、分解因式分解到不能分解为止.
2x4-32y4
例题讲解
=2(x2+4y2)(x2-4y2)
= 2(x2+4y2)(x+2y)(x-2y)
=2(x4-16y4)
1.把下列各式分解因式
(1)16a - 1 (4) a3x2 – a3y2
( 2 ) 4x - m n
( 3 ) –9x + 4
解:(1)16a -1=(4a) - 1
=(4a+1)(4a-1)
解:(2) 4x - m n
=(2x) - (mn)
=(2x+mn)(2x-mn)
解:(3) –9x + 4
(加法交换律)
= 22 – ( 3x ) 2
=(2+3x)(2-3x)
=4 - 9x
四、牛刀小试
解:a3x2 – a3y2
=a3 (x2 –y2)
=a3 (x+y)(x-y)
有公因式的要先提公因式
能写成( )2-( )2的式子,可以用平方差公式分解因式。
公式中的a , b可以是单独的数字、字母、单项式、多项式。
分解因式,有公因式时先“提”后“公”,应进行到每一个多项式因式不能再分解为止。
七、作业布置
课本45页1、练习第2题
2、习题12.5第1题
2、判断下列变形过程,哪些是因式分解?
(1) (x+2)(x-2)=x2- 4 ( )
(2) x2- 4+3x=(x+2)(x-2)+3x ( )
(3) 7m-7n-7=7(m-n-1) ( )
(4) 4x2- 9 =(2x+3)(2x- 3 ) ( )
×
×
√
√
1、什么叫多项式的因式分解
把一个多项式化为几个整式乘积的形式,叫做多项式的因式分解
一、复习引入
a米
b米
b米
a米
(a-b)
二、探究新知
如图,在边长为a米的正方形上剪掉一个边长为b米的小正方形,将剩余部分拼成一个长方形,根据此图形变换,你能得到什么公式?
a2- b2=(a+b)(a-b)
二、探索新知
用平方差公式进行因式分解
1、想一想:观察这个等式,从左到右是分解因式吗?
这和我们以前学过的什么知识很相似
利用平方差公式的逆运算—→分解因式
)
)(
(
b
a
b
a
-
+
=
2
2
b
a
-
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
整式乘法
因式分解
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
平方差公式:
a2 b2= (a+b)(a b)
□2-△2=(□+△)(□-△)
☆2-○2=(☆+○)(☆-○)
说说平方差公式的特点
两数的和与差的积
两个数的平方差;只有两项
形象地表示为
①左边
②右边
相同项
相反项
2、议一议
√
√
×
×
3、辨一辨
下列多项式能否用平方差公式来分解因式,为什么?
√
√
★符合平方差的形式的多项式才能用平方差公式进行因式分解,即能写成: ( )2-( )2的形式.
(1)x2+y2
(2)x2-y2
(3)-x2-y2
-(x2+y2)
y2-x2
(4)-x2+y2
(5)x2-25y2
(x+5y)(x-5y)
(6)m2-1
(m+1)(m-1)
你会填下列各空吗?
(1)4x2=( )2 25m2=( )2
(2) a4=( )2 0.49b2=( )2
(3) x4y2-4
(4) x2-0.01y2
9
49
=( )2-( )2
=( )2-( )2
x2y
2
0.1y
3
7
x
公式:(ab)n=anbn
4、练一练:
2x
5m
a2
0.7b
把下列各式分解因式
(1) 1-25x2
解: 1-25x2
1、把两项写成平方的形式,找出a和b
2、利用a2-b2=(a-b)(a+b)
分解因式
=12-(5x)2
=(1+5x)(1-5x)
(2)4x - m n
=(2x)2-(mn)2
=(2x+mn)(2x-mn)
三、典例精析
把下列各式分解因式
法一:
原式=
变式:-25x2
+1
+1
-25x2
(前后两项利用加法交换律交换位置)
=12-(5x)2
=(1+5x)(1-5x)
法二:
原式=-( 25x2 )
(把各项先提出一个“负号”)
=-[(5x)2-12]
=-(5x+1)(5x-1)
-1
例3:分解因式: (1) x5-x3
解:(1)
x5-x3 =
x3
(x2 –1)
= x3 (x+1)(x-1)
结论:
1、若有公因式,要先提公因式,再考虑 平方差公式.
2、分解因式分解到不能分解为止.
2x4-32y4
例题讲解
=2(x2+4y2)(x2-4y2)
= 2(x2+4y2)(x+2y)(x-2y)
=2(x4-16y4)
1.把下列各式分解因式
(1)16a - 1 (4) a3x2 – a3y2
( 2 ) 4x - m n
( 3 ) –9x + 4
解:(1)16a -1=(4a) - 1
=(4a+1)(4a-1)
解:(2) 4x - m n
=(2x) - (mn)
=(2x+mn)(2x-mn)
解:(3) –9x + 4
(加法交换律)
= 22 – ( 3x ) 2
=(2+3x)(2-3x)
=4 - 9x
四、牛刀小试
解:a3x2 – a3y2
=a3 (x2 –y2)
=a3 (x+y)(x-y)
有公因式的要先提公因式
能写成( )2-( )2的式子,可以用平方差公式分解因式。
公式中的a , b可以是单独的数字、字母、单项式、多项式。
分解因式,有公因式时先“提”后“公”,应进行到每一个多项式因式不能再分解为止。
七、作业布置
课本45页1、练习第2题
2、习题12.5第1题
