人教版数学七年级下册5.1.3同位角、内错角、同旁内角课件(共27张PPT)
文档属性
| 名称 | 人教版数学七年级下册5.1.3同位角、内错角、同旁内角课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 405.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览

文档简介
(共27张PPT)
七年级数学下 人教版
同位角、内错角、同旁内角
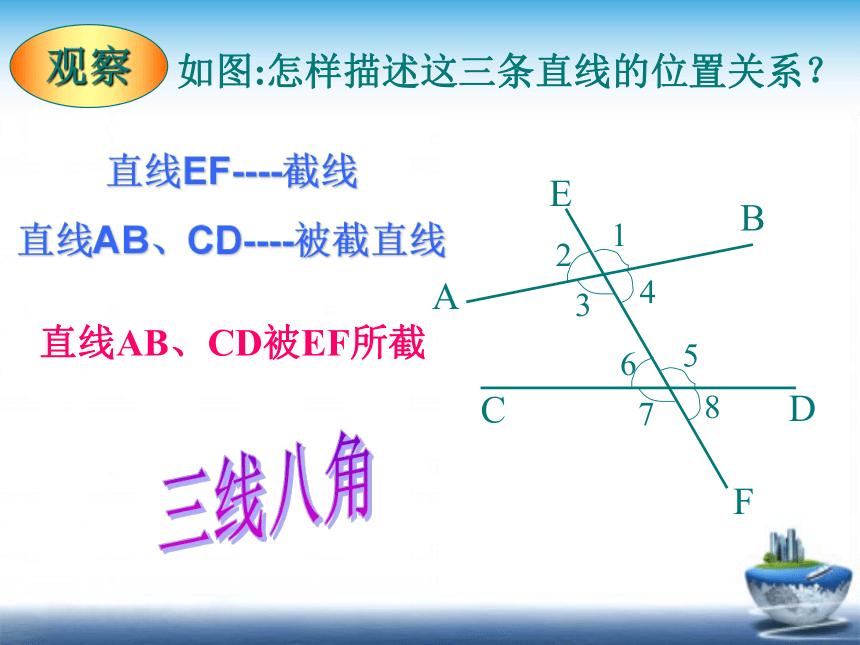
直线EF----截线
直线AB、CD----被截直线
直线AB、CD被EF所截
三线八角
如图:怎样描述这三条直线的位置关系?
观察
A
C
B
D
E
F
7
1
2
3
4
5
6
8
观察
F
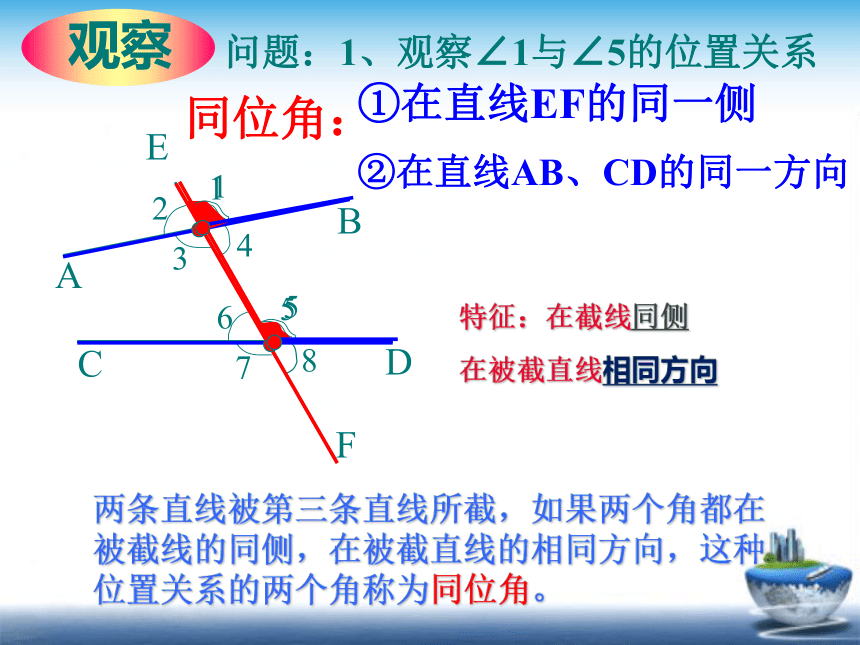
问题:1、观察∠1与∠5的位置关系
①在直线EF的同一侧
②在直线AB、CD的同一方向
A
C
B
D
E
1
2
3
4
5
6
7
8
同位角:
1
5
两条直线被第三条直线所截,如果两个角都在被截线的同侧,在被截直线的相同方向,这种位置关系的两个角称为同位角。
特征:在截线同侧
在被截直线相同方向
F
A
C
B
D
E
1
2
3
4
5
6
7
8
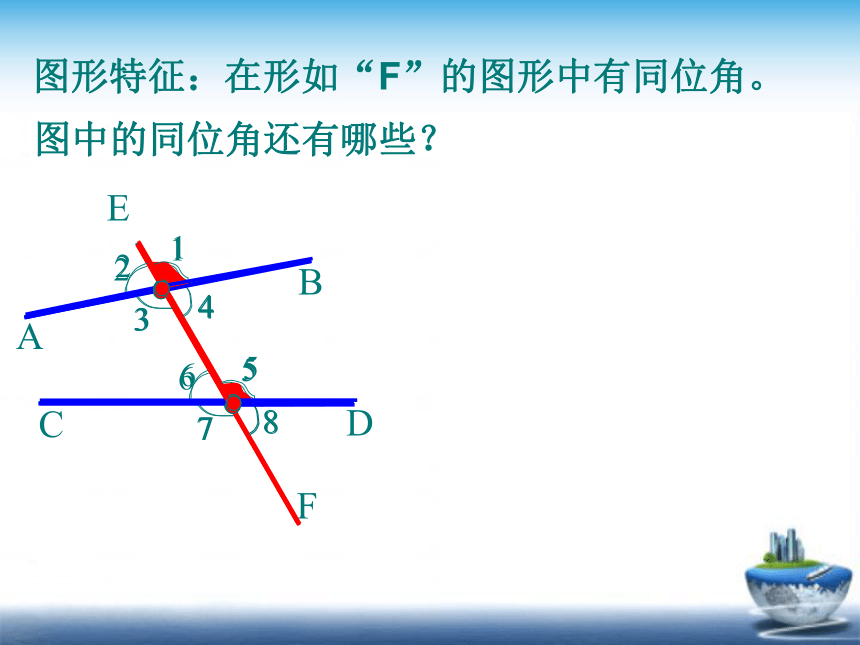
图中的同位角还有哪些?
2
6
3
7
4
8
1
5
图形特征:在形如“F”的图形中有同位角。
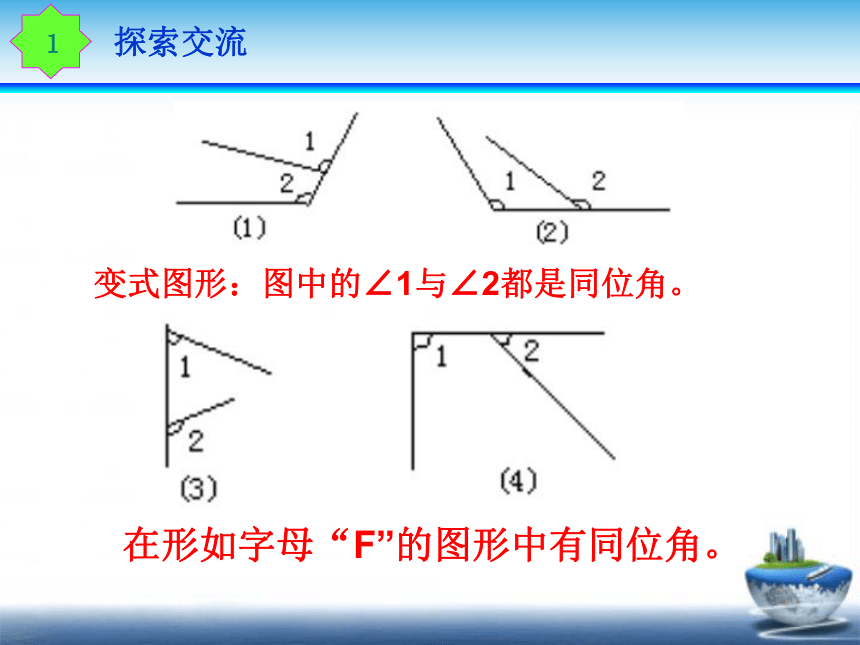
在形如字母“F”的图形中有同位角。
变式图形:图中的∠1与∠2都是同位角。
探索交流
1
A
C
B
D
E
F
1
2
3
4
5
6
7
8
观察
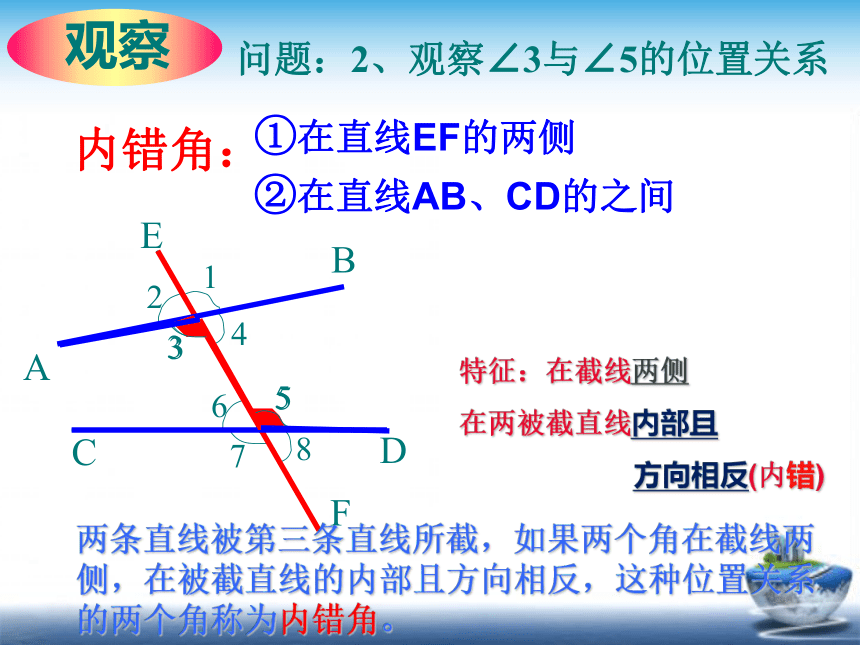
问题:2、观察∠3与∠5的位置关系
①在直线EF的两侧
②在直线AB、CD的之间
内错角:
3
5
两条直线被第三条直线所截,如果两个角在截线两侧,在被截直线的内部且方向相反,这种位置关系的两个角称为内错角。
特征:在截线两侧
在两被截直线内部且
方向相反(内错)
A
C
B
D
E
F
1
2
3
4
5
6
7
8
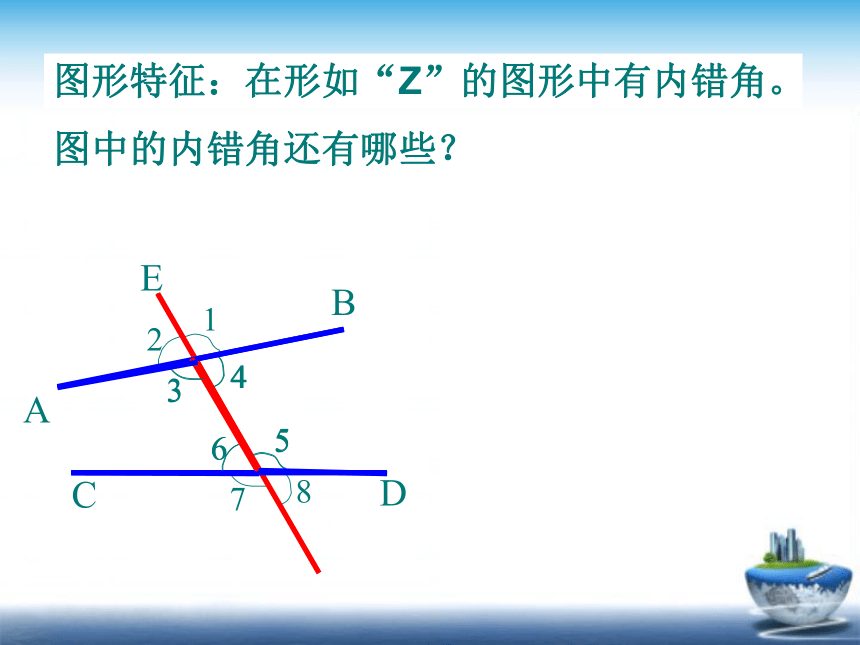
图中的内错角还有哪些?
图形特征:在形如“Z”的图形中有内错角。
4
6
3
5
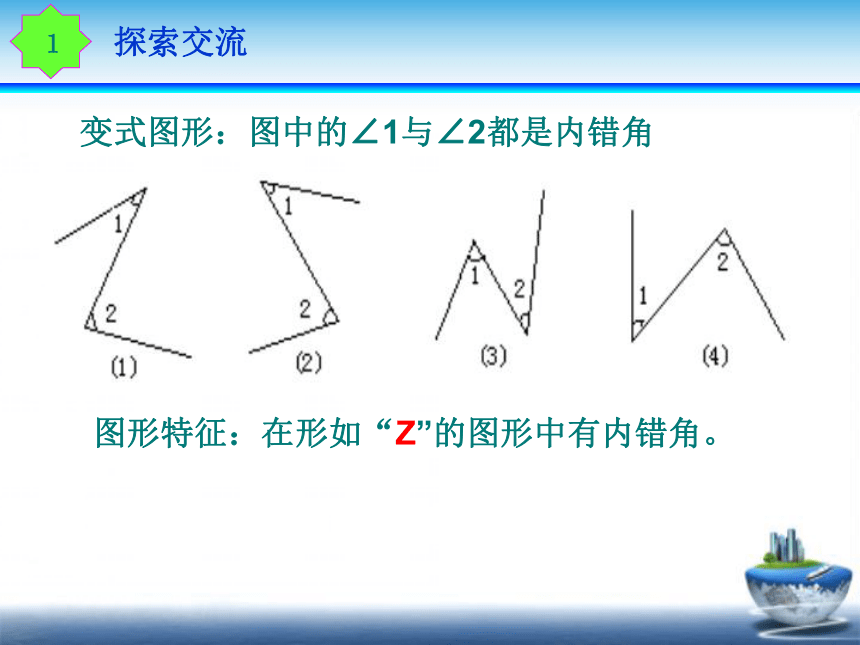
变式图形:图中的∠1与∠2都是内错角
图形特征:在形如“Z”的图形中有内错角。
探索交流
1
A
C
B
D
E
F
1
2
3
4
5
6
7
8
观察
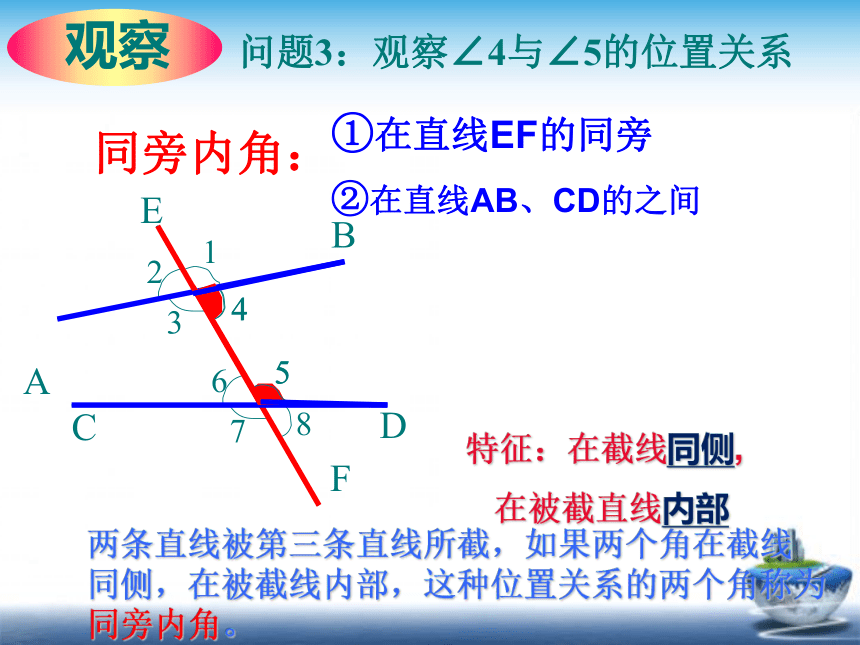
问题3:观察∠4与∠5的位置关系
①在直线EF的同旁
②在直线AB、CD的之间
同旁内角:
4
5
两条直线被第三条直线所截,如果两个角在截线
同侧,在被截线内部,这种位置关系的两个角称为同旁内角。
特征:在截线同侧,
在被截直线内部
4
5
图中还有哪些同旁内角?
图形特征:在形如“C”的图形中有同旁内角。
A
C
B
D
E
F
1
2
3
4
5
6
7
8
3
6
变式图形:图中的∠1与∠2都是同旁内角。
图形特征:在形如“C”的图形中有同旁内角。
探索交流
1
同位角、内错角和同旁内角的结构特征:
截线 被截线 结构特征
同位角
内错角
同旁内角
内部
相反方向
同方向
同侧
两侧
同侧
F
Z
C
请同学们分别用双手的大拇指,食指各组成一个角,两食指相对成一条线,保持在同一平面内,分别进行尝试,看可以组成哪些角。
试一试:
例题:
请同学们指出下列各图中∠1与∠2的关系。
2
1
1
2
1
2
1
2
1
2
①
③
④
⑤
②
内错角
同位角
同旁内角
同旁内角
内错角
选一选
如图,∠1和∠2不是同位角的是( )
1
2
1
2
1
1
2
2
(A)
(B)
(C)
(D)
a
b
O
M
c
a
b
c
E
F
M
N
a
b
c
E
F
M
N
a
b
c
D
能力挑战1: 看图填空
(1)若ED,BF被AB所截,
则∠1与_____是同位角。
∠2
(2)若ED,BC被AF所截,
则∠3与_____是内错角。
∠4
能力挑战2: 看图填空
(3)∠1与∠3是AB和AF被_____所截构成的_______角。
DE
内错
能力挑战3: 看图填空
(4)∠2与∠4是_____和_____被
BC所截构成的______角。
AB
AF
同位
能力挑战4: 看图填空
例:如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角?
(2)如果∠1=∠4,哪么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
D
E
C
B
A
2
4
3
1
例:如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角?
(2)如果∠1=∠4,哪么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
D
E
C
B
A
2
4
3
1
(1)∠1和∠2是内错角;∠1和∠3是同旁内角; ∠1和∠4是同位角。
(2)∵∠1=∠4(已知)
∠4=∠2
(对顶角相等)
∴∠1=∠2.
∵∠4+∠3=180°(邻补角定义)
∠1=∠4(已知)
∴∠1+∠3=180°
即∠1和∠3互补.
答:
3
2
4
1
c
b
a
找出图中的同位角、内错角、同旁内角:
1
2
E
D
A
C
B
图中与∠1是同旁内角的角:
1
E
D
A
C
B
1
A
C
B
1
2
A
C
B
图中∠2的同旁内角的角:
1
2
E
D
A
C
B
1
2
A
C
B
2
A
C
B
2
E
D
A
C
B
截线 被截线 结构特征
同位角
内错角
同旁内角
内部
相反方向
同方向
同侧
两侧
同侧
F
Z
C
小 结
这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,有三种情况:同位角、内错角、同旁内角。
1、两条直线被第三条直线所截,
如何判定两个角的位置关系?
2、如何确定截线和被截线?
——划掉无关,排除干扰,描图想象
——两个角的公共直线为截线,
非公共直线则为被截线。
例
如图:直线DE交∠ABC的边BA于点 F. 如果内错角∠1与∠2相等,那么你能找出图中其它相等的角吗?请说明理由。
4
A
C
B
D
E
F
1
2
3
有互补的角吗?
同位角∠1与∠4相等
同旁内角∠1与∠3互补
七年级数学下 人教版
同位角、内错角、同旁内角
直线EF----截线
直线AB、CD----被截直线
直线AB、CD被EF所截
三线八角
如图:怎样描述这三条直线的位置关系?
观察
A
C
B
D
E
F
7
1
2
3
4
5
6
8
观察
F
问题:1、观察∠1与∠5的位置关系
①在直线EF的同一侧
②在直线AB、CD的同一方向
A
C
B
D
E
1
2
3
4
5
6
7
8
同位角:
1
5
两条直线被第三条直线所截,如果两个角都在被截线的同侧,在被截直线的相同方向,这种位置关系的两个角称为同位角。
特征:在截线同侧
在被截直线相同方向
F
A
C
B
D
E
1
2
3
4
5
6
7
8
图中的同位角还有哪些?
2
6
3
7
4
8
1
5
图形特征:在形如“F”的图形中有同位角。
在形如字母“F”的图形中有同位角。
变式图形:图中的∠1与∠2都是同位角。
探索交流
1
A
C
B
D
E
F
1
2
3
4
5
6
7
8
观察
问题:2、观察∠3与∠5的位置关系
①在直线EF的两侧
②在直线AB、CD的之间
内错角:
3
5
两条直线被第三条直线所截,如果两个角在截线两侧,在被截直线的内部且方向相反,这种位置关系的两个角称为内错角。
特征:在截线两侧
在两被截直线内部且
方向相反(内错)
A
C
B
D
E
F
1
2
3
4
5
6
7
8
图中的内错角还有哪些?
图形特征:在形如“Z”的图形中有内错角。
4
6
3
5
变式图形:图中的∠1与∠2都是内错角
图形特征:在形如“Z”的图形中有内错角。
探索交流
1
A
C
B
D
E
F
1
2
3
4
5
6
7
8
观察
问题3:观察∠4与∠5的位置关系
①在直线EF的同旁
②在直线AB、CD的之间
同旁内角:
4
5
两条直线被第三条直线所截,如果两个角在截线
同侧,在被截线内部,这种位置关系的两个角称为同旁内角。
特征:在截线同侧,
在被截直线内部
4
5
图中还有哪些同旁内角?
图形特征:在形如“C”的图形中有同旁内角。
A
C
B
D
E
F
1
2
3
4
5
6
7
8
3
6
变式图形:图中的∠1与∠2都是同旁内角。
图形特征:在形如“C”的图形中有同旁内角。
探索交流
1
同位角、内错角和同旁内角的结构特征:
截线 被截线 结构特征
同位角
内错角
同旁内角
内部
相反方向
同方向
同侧
两侧
同侧
F
Z
C
请同学们分别用双手的大拇指,食指各组成一个角,两食指相对成一条线,保持在同一平面内,分别进行尝试,看可以组成哪些角。
试一试:
例题:
请同学们指出下列各图中∠1与∠2的关系。
2
1
1
2
1
2
1
2
1
2
①
③
④
⑤
②
内错角
同位角
同旁内角
同旁内角
内错角
选一选
如图,∠1和∠2不是同位角的是( )
1
2
1
2
1
1
2
2
(A)
(B)
(C)
(D)
a
b
O
M
c
a
b
c
E
F
M
N
a
b
c
E
F
M
N
a
b
c
D
能力挑战1: 看图填空
(1)若ED,BF被AB所截,
则∠1与_____是同位角。
∠2
(2)若ED,BC被AF所截,
则∠3与_____是内错角。
∠4
能力挑战2: 看图填空
(3)∠1与∠3是AB和AF被_____所截构成的_______角。
DE
内错
能力挑战3: 看图填空
(4)∠2与∠4是_____和_____被
BC所截构成的______角。
AB
AF
同位
能力挑战4: 看图填空
例:如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角?
(2)如果∠1=∠4,哪么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
D
E
C
B
A
2
4
3
1
例:如图直线DE、BC被直线AB所截,
(1)∠1和∠2、∠1和∠3、∠1和∠4各是什么角?
(2)如果∠1=∠4,哪么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
D
E
C
B
A
2
4
3
1
(1)∠1和∠2是内错角;∠1和∠3是同旁内角; ∠1和∠4是同位角。
(2)∵∠1=∠4(已知)
∠4=∠2
(对顶角相等)
∴∠1=∠2.
∵∠4+∠3=180°(邻补角定义)
∠1=∠4(已知)
∴∠1+∠3=180°
即∠1和∠3互补.
答:
3
2
4
1
c
b
a
找出图中的同位角、内错角、同旁内角:
1
2
E
D
A
C
B
图中与∠1是同旁内角的角:
1
E
D
A
C
B
1
A
C
B
1
2
A
C
B
图中∠2的同旁内角的角:
1
2
E
D
A
C
B
1
2
A
C
B
2
A
C
B
2
E
D
A
C
B
截线 被截线 结构特征
同位角
内错角
同旁内角
内部
相反方向
同方向
同侧
两侧
同侧
F
Z
C
小 结
这节课研究的是两条直线被第三条直线所截形成的不同顶点处的两个角之间的位置关系,有三种情况:同位角、内错角、同旁内角。
1、两条直线被第三条直线所截,
如何判定两个角的位置关系?
2、如何确定截线和被截线?
——划掉无关,排除干扰,描图想象
——两个角的公共直线为截线,
非公共直线则为被截线。
例
如图:直线DE交∠ABC的边BA于点 F. 如果内错角∠1与∠2相等,那么你能找出图中其它相等的角吗?请说明理由。
4
A
C
B
D
E
F
1
2
3
有互补的角吗?
同位角∠1与∠4相等
同旁内角∠1与∠3互补
