2021—2022学年人教版九年级数学上册24.3正多边形和圆课后练习(word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学上册24.3正多边形和圆课后练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 215.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 07:49:34 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学上册 第二十四章 圆 24.3正多边形和圆 课后练习
一、选择题
1.等边三角形的外接圆面积是内切圆面积的( )
A.3倍 B.5倍 C.4倍 D.2倍
2.若正六边形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6, B.,3 C.6,3 D.,
3.正六边形的边心距为,则该正六边形的外接圆半径为( )
A. B.2 C.3 D.
4.如图,正方形内接于.点为上一点,连接、,若,,则的长为( )
A. B. C. D.
5.如图,在⊙O中,点B是弧AC上的一点,∠AOC=140°,则∠ABC的度数为( )
A.70° B.110° C.120° D.140°
6.如图,已知的半径为,内接于,,则( )
A. B. C. D.
7.如图,六边形是正六边形,点是边的中点,,分别与交于点,,则的值为( ).
A. B. C. D.
8.如图,点,,在上,若,,分别是内接正三角形.正方形,正边形的一边,则( )
A.9 B.10 C.12 D.15
9.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形, BC∥QR,则∠AOQ=( )
A.60° B.65° C.72° D.75°
10.如图所示,八边形ABCDEFGH是正八边形,其外接⊙O的半径为,则正八边形的面积S为( ).
A. B. C.8 D.4
二、填空题
11.如图,四边形ABCD内接于⊙O,∠A=115°,则∠BOD=_______.
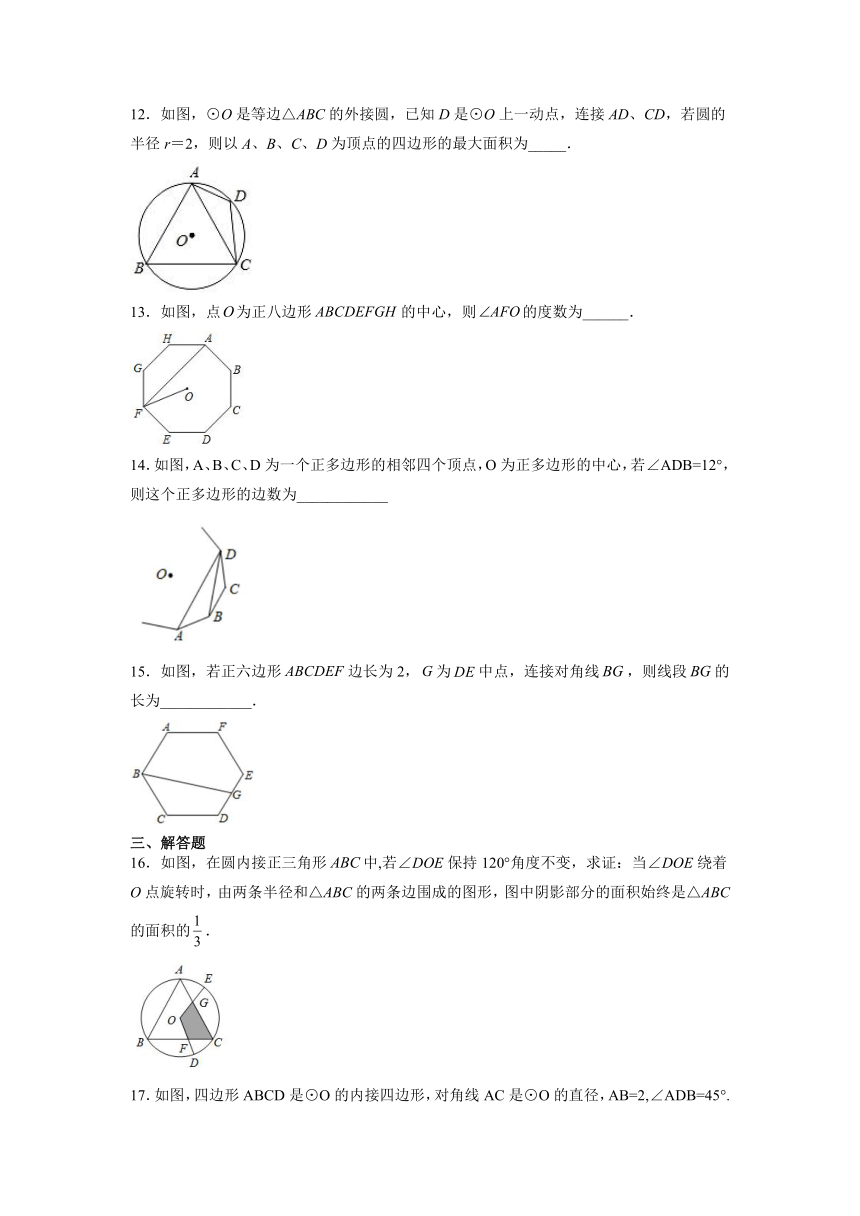
12.如图,⊙O是等边△ABC的外接圆,已知D是⊙O上一动点,连接AD、CD,若圆的半径r=2,则以A、B、C、D为顶点的四边形的最大面积为_____.
13.如图,点为正八边形的中心,则的度数为______.
14.如图,A、B、C、D为一个正多边形的相邻四个顶点,O为正多边形的中心,若∠ADB=12°,则这个正多边形的边数为____________
15.如图,若正六边形边长为2,为中点,连接对角线,则线段的长为____________.
三、解答题
16.如图,在圆内接正三角形中,若∠DOE保持120°角度不变,求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形,图中阴影部分的面积始终是△ABC的面积的.
17.如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,∠ADB=45°. 求⊙O半径的长.
18.如图,正五边形内接于,为上的一点(点不与点重合),求的余角的度数.
19.已知,如图,四边形ABCD的顶点都在同一个圆上,且∠A:∠B:∠C=2:3:4.
(1)求∠A、∠B的度数;
(2)若D为的中点,AB=4,BC=3,求四边形ABCD的面积.
20.如图,正方形内接于,为上的一点,连接,.
(1)求的度数;
(2)当点为的中点时,是的内接正边形的一边,求的值.
21.如图,正方形内接于,为任意一点,连接、.
(1)求的度数.
(2)如图2,过点作交于点,连接,,,求的长度.
22.如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度中⊙O上逆时针运动.
(1)求图①中∠APB的度数;
(2)图②中,∠APB的度数是 90°,图③中∠APB的度数是 72°;
(3)根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.
23.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
(1)求图1中∠MON的度数
(2)图2中∠MON的度数是 ,图3中∠MON的度数是
(3)试探究∠MON的度数与正n边形边数n的关系是____
【参考答案】
1.C 2.A 3.B 4.D 5.B 6.C 7.D 8.C 9.D 10.B
11.130°
12.4.
13..
14.15
15.
16.如图:连接OA、OB、OC,
由正多边形和圆的性质可得△OAB≌△OBC≌△OCA.
∴ ∠1=∠2.
设OD交BC于F,OE交AC于G,则∠AOC=∠3+∠4=120°,
∠DOE=∠5+∠4=120°,
∴ ∠3=∠5.
在△OAG和△OCF中,
∴ △OAG≌△OCF.
∴
17..
18.54°
19.(1)60°、90°;(2)
20.(1)45°;(2)8
21.(1)45°;(2)
22.(1)120°;(2)=,=;(3)能,∠APB=
23.(1);(2),;(3)
一、选择题
1.等边三角形的外接圆面积是内切圆面积的( )
A.3倍 B.5倍 C.4倍 D.2倍
2.若正六边形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A.6, B.,3 C.6,3 D.,
3.正六边形的边心距为,则该正六边形的外接圆半径为( )
A. B.2 C.3 D.
4.如图,正方形内接于.点为上一点,连接、,若,,则的长为( )
A. B. C. D.
5.如图,在⊙O中,点B是弧AC上的一点,∠AOC=140°,则∠ABC的度数为( )
A.70° B.110° C.120° D.140°
6.如图,已知的半径为,内接于,,则( )
A. B. C. D.
7.如图,六边形是正六边形,点是边的中点,,分别与交于点,,则的值为( ).
A. B. C. D.
8.如图,点,,在上,若,,分别是内接正三角形.正方形,正边形的一边,则( )
A.9 B.10 C.12 D.15
9.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形, BC∥QR,则∠AOQ=( )
A.60° B.65° C.72° D.75°
10.如图所示,八边形ABCDEFGH是正八边形,其外接⊙O的半径为,则正八边形的面积S为( ).
A. B. C.8 D.4
二、填空题
11.如图,四边形ABCD内接于⊙O,∠A=115°,则∠BOD=_______.
12.如图,⊙O是等边△ABC的外接圆,已知D是⊙O上一动点,连接AD、CD,若圆的半径r=2,则以A、B、C、D为顶点的四边形的最大面积为_____.
13.如图,点为正八边形的中心,则的度数为______.
14.如图,A、B、C、D为一个正多边形的相邻四个顶点,O为正多边形的中心,若∠ADB=12°,则这个正多边形的边数为____________
15.如图,若正六边形边长为2,为中点,连接对角线,则线段的长为____________.
三、解答题
16.如图,在圆内接正三角形中,若∠DOE保持120°角度不变,求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形,图中阴影部分的面积始终是△ABC的面积的.
17.如图,四边形ABCD是⊙O的内接四边形,对角线AC是⊙O的直径,AB=2,∠ADB=45°. 求⊙O半径的长.
18.如图,正五边形内接于,为上的一点(点不与点重合),求的余角的度数.
19.已知,如图,四边形ABCD的顶点都在同一个圆上,且∠A:∠B:∠C=2:3:4.
(1)求∠A、∠B的度数;
(2)若D为的中点,AB=4,BC=3,求四边形ABCD的面积.
20.如图,正方形内接于,为上的一点,连接,.
(1)求的度数;
(2)当点为的中点时,是的内接正边形的一边,求的值.
21.如图,正方形内接于,为任意一点,连接、.
(1)求的度数.
(2)如图2,过点作交于点,连接,,,求的长度.
22.如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度中⊙O上逆时针运动.
(1)求图①中∠APB的度数;
(2)图②中,∠APB的度数是 90°,图③中∠APB的度数是 72°;
(3)根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.
23.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
(1)求图1中∠MON的度数
(2)图2中∠MON的度数是 ,图3中∠MON的度数是
(3)试探究∠MON的度数与正n边形边数n的关系是____
【参考答案】
1.C 2.A 3.B 4.D 5.B 6.C 7.D 8.C 9.D 10.B
11.130°
12.4.
13..
14.15
15.
16.如图:连接OA、OB、OC,
由正多边形和圆的性质可得△OAB≌△OBC≌△OCA.
∴ ∠1=∠2.
设OD交BC于F,OE交AC于G,则∠AOC=∠3+∠4=120°,
∠DOE=∠5+∠4=120°,
∴ ∠3=∠5.
在△OAG和△OCF中,
∴ △OAG≌△OCF.
∴
17..
18.54°
19.(1)60°、90°;(2)
20.(1)45°;(2)8
21.(1)45°;(2)
22.(1)120°;(2)=,=;(3)能,∠APB=
23.(1);(2),;(3)
同课章节目录
