等比数列2
图片预览





文档简介
课件19张PPT。等比数列(2) 一般地,如果一个数列从第二项起每
一项与它的前一项的比等于同一个常数,那
么这个数列就叫做等比数列,这个常数叫做
等比数列的公比,公比通常用字母q表示(q≠0) 。问:数列a, a, a, a, …(a∈R)是否为等比数列?
如果是,a必须满足什么条件?(1) a=0; 它只是等差数列。
(2) a≠0; 它既是等差数列又是等比数列。1.定义:三、如果在a与b中间插入一个数G,使a,G,b
成等比数列,那么G叫做a与b的等比中项。等比数列的通项公式练习1求下列等比数列的第4,5项:(2)1.2,2.4,4.8,… (1) 5,-15,45,… 1 、培育水稻新品种,如果第1代得到120粒种子,并且从第1代起,以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代大约可以得到这种新品种的种子多少粒(保留两个有效数字)?解:由于每代的种子数是它的
前一代种子数的120倍,因此,逐代的种子数组成
等比数列,记为 等比数列的通项公式练习若原价格为a,则降价x后的价格应为
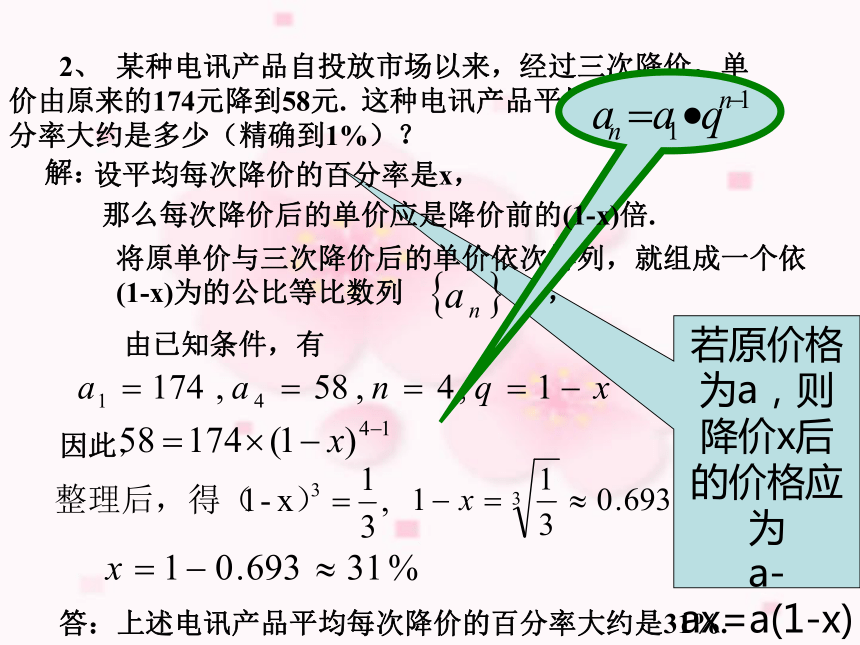
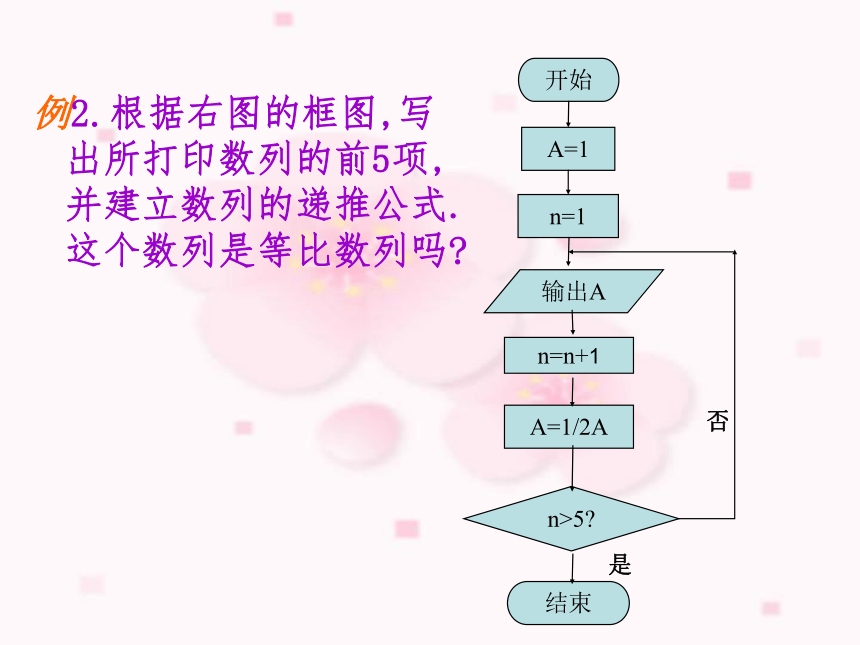
a-ax=a(1-x) 2、 某种电讯产品自投放市场以来,经过三次降价,单价由原来的174元降到58元. 这种电讯产品平均每次降价的百分率大约是多少(精确到1%)? 解:将原单价与三次降价后的单价依次排列,就组成一个依(1-x)为的公比等比数列 ,由已知条件,有因此,答:上述电讯产品平均每次降价的百分率大约是31%.设平均每次降价的百分率是x,那么每次降价后的单价应是降价前的(1-x)倍.是例2.根据右图的框图,写出所打印数列的前5项,并建立数列的递推公式.这个数列是等比数列吗?例3.一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项.(分析:要求第1项和第2项,必先求公比q.
可利用方程的思想进行求解。)探究是知识拓展一、通项公式的推广定义法:二、判断等比数列的方法中项法:三个数a,b,c成等比数列4、等比数列所有奇数项符号相同;
所有偶数项符号相同。三、等比数列的性质5、等比数列中,项数成等差数列的项构成新的数列,则这列数列也为等比数列 等比数列的性质练习1.在等比数列 ,已知 ,求 解:∵ 2.在等比数列 中, ,求该数列前七项之积。 解: ∴前七项之积 等比数列的性质练习3.在等比数列 ,已知 ,求 解: 另解:∵ 是 与 的等比中项,∴ ∴ 等比数列的性质例题例1 已知 是等比数列,且 求 解:∵ 是等比数列, ∴ ∴ ∴ 等比数列的性质例题例2 a≠c,三数a, 1, c成等差数列, 成等比数列,求 解:∵a, 1, c成等差数列, ∴ a+c=2, 又 成等比数列,∴ 有ac=1或ac=-1, 当ac=1时, 由a+c=2得a=1, c=1,与a≠c矛盾,∴ ac=-1, 1.定义2.公比(差)3.等比(差)
中项4.通项公式5.性质
(若m+n=p+q)q不可以是0,d可以是0等比中项等差中项
一项与它的前一项的比等于同一个常数,那
么这个数列就叫做等比数列,这个常数叫做
等比数列的公比,公比通常用字母q表示(q≠0) 。问:数列a, a, a, a, …(a∈R)是否为等比数列?
如果是,a必须满足什么条件?(1) a=0; 它只是等差数列。
(2) a≠0; 它既是等差数列又是等比数列。1.定义:三、如果在a与b中间插入一个数G,使a,G,b
成等比数列,那么G叫做a与b的等比中项。等比数列的通项公式练习1求下列等比数列的第4,5项:(2)1.2,2.4,4.8,… (1) 5,-15,45,… 1 、培育水稻新品种,如果第1代得到120粒种子,并且从第1代起,以后各代的每一粒种子都可以得到下一代的120粒种子,到第5代大约可以得到这种新品种的种子多少粒(保留两个有效数字)?解:由于每代的种子数是它的
前一代种子数的120倍,因此,逐代的种子数组成
等比数列,记为 等比数列的通项公式练习若原价格为a,则降价x后的价格应为
a-ax=a(1-x) 2、 某种电讯产品自投放市场以来,经过三次降价,单价由原来的174元降到58元. 这种电讯产品平均每次降价的百分率大约是多少(精确到1%)? 解:将原单价与三次降价后的单价依次排列,就组成一个依(1-x)为的公比等比数列 ,由已知条件,有因此,答:上述电讯产品平均每次降价的百分率大约是31%.设平均每次降价的百分率是x,那么每次降价后的单价应是降价前的(1-x)倍.是例2.根据右图的框图,写出所打印数列的前5项,并建立数列的递推公式.这个数列是等比数列吗?例3.一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项.(分析:要求第1项和第2项,必先求公比q.
可利用方程的思想进行求解。)探究是知识拓展一、通项公式的推广定义法:二、判断等比数列的方法中项法:三个数a,b,c成等比数列4、等比数列所有奇数项符号相同;
所有偶数项符号相同。三、等比数列的性质5、等比数列中,项数成等差数列的项构成新的数列,则这列数列也为等比数列 等比数列的性质练习1.在等比数列 ,已知 ,求 解:∵ 2.在等比数列 中, ,求该数列前七项之积。 解: ∴前七项之积 等比数列的性质练习3.在等比数列 ,已知 ,求 解: 另解:∵ 是 与 的等比中项,∴ ∴ 等比数列的性质例题例1 已知 是等比数列,且 求 解:∵ 是等比数列, ∴ ∴ ∴ 等比数列的性质例题例2 a≠c,三数a, 1, c成等差数列, 成等比数列,求 解:∵a, 1, c成等差数列, ∴ a+c=2, 又 成等比数列,∴ 有ac=1或ac=-1, 当ac=1时, 由a+c=2得a=1, c=1,与a≠c矛盾,∴ ac=-1, 1.定义2.公比(差)3.等比(差)
中项4.通项公式5.性质
(若m+n=p+q)q不可以是0,d可以是0等比中项等差中项
