沪科版数学九年级上册 23.2 解直角三角形(课件)(共18张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 23.2 解直角三角形(课件)(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 622.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
解直角三角形
世界上最高的电视塔--广州电视塔。
30°
1050米
?
1.在Rt△ABC中共有几个基本元素?哪几个?
6个,三条边:a、b、c 三个角:∠A 、∠B 、∠C
2.如图,在Rt△ABC中,∠C=90°,除了直角外,
还有几个元素?哪几个元素?
A
C
B
c
b
a
5个
问题:
,两个锐角∠A 、∠B 、三条边a、b、c
3.如图,在Rt△ABC中,a、b、c, ∠A 、∠B,这五个元素间有怎样的关系呢 ?
A
C
B
c
b
a
(1)三边之间关系:
(2)锐角之间关系:
(3)边角之间关系:
a2+b2=c2
∠A +∠B=90°
(勾股定理)
(互余)
(三角函数)
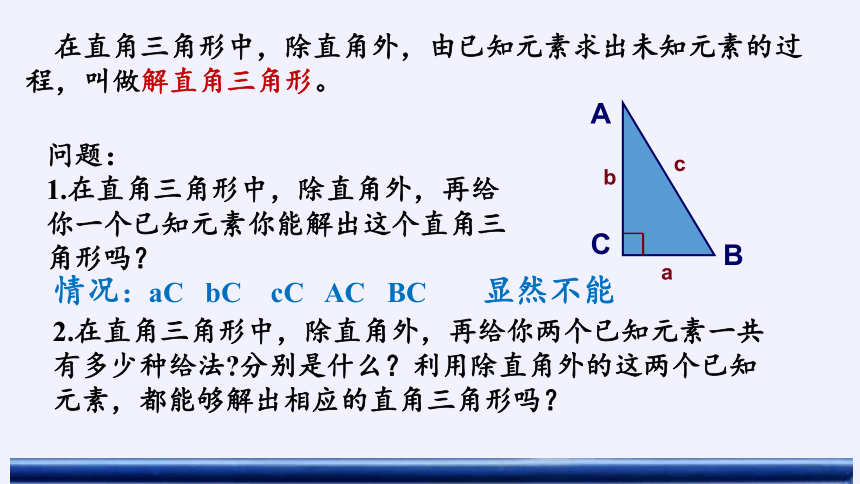
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形。
问题:
1.在直角三角形中,除直角外,再给你一个已知元素你能解出这个直角三角形吗?
A
C
B
c
b
a
2.在直角三角形中,除直角外,再给你两个已知元素一共有多少种给法 分别是什么?利用除直角外的这两个已知元素,都能够解出相应的直角三角形吗?
情况:aC bC cC AC BC
显然不能
a
b
c
A
B
已知元素
1
2
3
4
5
6
7
8
9
10
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
a c
a b
a A
a B
b c
c A
c B
b A
A B
b B
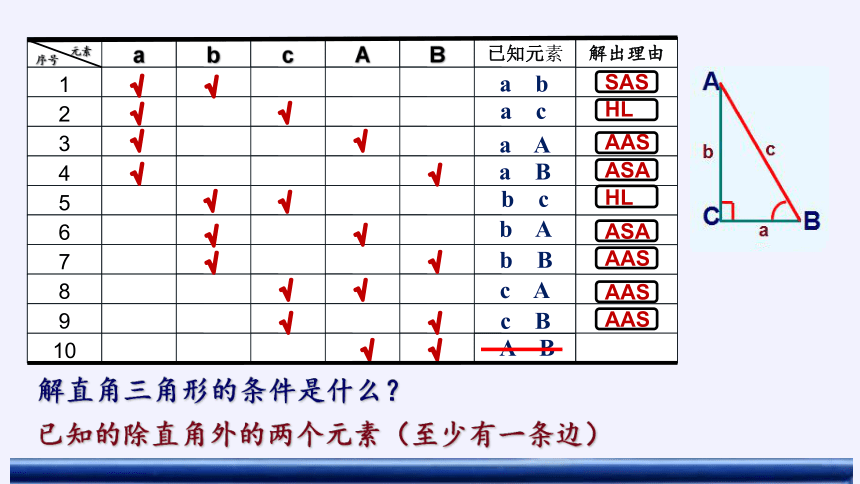
解直角三角形的条件是什么?
已知的除直角外的两个元素(至少有一条边)
元素
序号
解出理由
SAS
HL
AAS
ASA
HL
ASA
AAS
AAS
AAS
A
C
B
c
b
a
a A
a B
b A
A B
b B
已知元素
A
C
B
c
b
a
a b
a c
b c
c A
c B
a b
a c
b c
a A
a B
c A
c B
b B
b A
已知两边
已知一边一角
如图,在Rt△ABC中,∠C=90°,a=1,b= ,解这个直角三角形。
A
C
B
c
b
a
已知一边一角
已知两边
解直角三角形
用勾股定理求另一边
选恰当三角函数关系式求角
用互余关系或三角函数关系式求另外一角
如图,在Rt△ABC中,∠C=90°,∠B=53°,c=5,
解这个直角三角形。
已知两边
解直角三角形
已知一边一角
A
C
B
c
b
a
解:如图
先求另一角
用三角函数关系求另两边或先求一边,利用勾股定理求另一边。
先求另外一角,然后选取恰当的三角函数关系求另外两个边或先求一边,利用勾股定理求另外一边。
先求另外一个边,然后选取恰当的三角函数关系求另两角,或先求一角,利用互余求另一角。
解直角三角形
已知一边一角
已知两边
A
C
H
练习:在△ABC中,∠A=55°,b=20cm,c=30cm。
求这个三角形的面积。
解 如图,作AB边上的高CD.
C
A
B
a
b
c
D
练习:在△ABC中,∠A=55°,b=20cm,c=30cm。
求这个三角形的面积。
解 如图,作AB边上的高CM.
C
A
B
a
b
c
M
1.△ABC中, ∠B=60°, a=3cm,c=4cm。
则S △ABC为多少?
2.
练习:
30°
C
A
H
60°
E
700米
通过本节课学习,我们学习了哪些内容?
1.解直角三角形的概念
2.解直角三角形的依据
3.解直角三角形的条件
4.如何利用直角三角形(除直角外)两个已知元素,(至少有一个是边)去求其余元素。
5.解直角三角形的简单应用
作业布置
必做题:同步练习23.2(一)第1-8题
思考题:同步练习23.2(一)第9题
谢 谢
解直角三角形
世界上最高的电视塔--广州电视塔。
30°
1050米
?
1.在Rt△ABC中共有几个基本元素?哪几个?
6个,三条边:a、b、c 三个角:∠A 、∠B 、∠C
2.如图,在Rt△ABC中,∠C=90°,除了直角外,
还有几个元素?哪几个元素?
A
C
B
c
b
a
5个
问题:
,两个锐角∠A 、∠B 、三条边a、b、c
3.如图,在Rt△ABC中,a、b、c, ∠A 、∠B,这五个元素间有怎样的关系呢 ?
A
C
B
c
b
a
(1)三边之间关系:
(2)锐角之间关系:
(3)边角之间关系:
a2+b2=c2
∠A +∠B=90°
(勾股定理)
(互余)
(三角函数)
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形。
问题:
1.在直角三角形中,除直角外,再给你一个已知元素你能解出这个直角三角形吗?
A
C
B
c
b
a
2.在直角三角形中,除直角外,再给你两个已知元素一共有多少种给法 分别是什么?利用除直角外的这两个已知元素,都能够解出相应的直角三角形吗?
情况:aC bC cC AC BC
显然不能
a
b
c
A
B
已知元素
1
2
3
4
5
6
7
8
9
10
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
a c
a b
a A
a B
b c
c A
c B
b A
A B
b B
解直角三角形的条件是什么?
已知的除直角外的两个元素(至少有一条边)
元素
序号
解出理由
SAS
HL
AAS
ASA
HL
ASA
AAS
AAS
AAS
A
C
B
c
b
a
a A
a B
b A
A B
b B
已知元素
A
C
B
c
b
a
a b
a c
b c
c A
c B
a b
a c
b c
a A
a B
c A
c B
b B
b A
已知两边
已知一边一角
如图,在Rt△ABC中,∠C=90°,a=1,b= ,解这个直角三角形。
A
C
B
c
b
a
已知一边一角
已知两边
解直角三角形
用勾股定理求另一边
选恰当三角函数关系式求角
用互余关系或三角函数关系式求另外一角
如图,在Rt△ABC中,∠C=90°,∠B=53°,c=5,
解这个直角三角形。
已知两边
解直角三角形
已知一边一角
A
C
B
c
b
a
解:如图
先求另一角
用三角函数关系求另两边或先求一边,利用勾股定理求另一边。
先求另外一角,然后选取恰当的三角函数关系求另外两个边或先求一边,利用勾股定理求另外一边。
先求另外一个边,然后选取恰当的三角函数关系求另两角,或先求一角,利用互余求另一角。
解直角三角形
已知一边一角
已知两边
A
C
H
练习:在△ABC中,∠A=55°,b=20cm,c=30cm。
求这个三角形的面积。
解 如图,作AB边上的高CD.
C
A
B
a
b
c
D
练习:在△ABC中,∠A=55°,b=20cm,c=30cm。
求这个三角形的面积。
解 如图,作AB边上的高CM.
C
A
B
a
b
c
M
1.△ABC中, ∠B=60°, a=3cm,c=4cm。
则S △ABC为多少?
2.
练习:
30°
C
A
H
60°
E
700米
通过本节课学习,我们学习了哪些内容?
1.解直角三角形的概念
2.解直角三角形的依据
3.解直角三角形的条件
4.如何利用直角三角形(除直角外)两个已知元素,(至少有一个是边)去求其余元素。
5.解直角三角形的简单应用
作业布置
必做题:同步练习23.2(一)第1-8题
思考题:同步练习23.2(一)第9题
谢 谢
