内蒙古呼伦贝尔市牙林一中2012-2013学年高二上学期期中考试数学(文)试题
文档属性
| 名称 | 内蒙古呼伦贝尔市牙林一中2012-2013学年高二上学期期中考试数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 159.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-31 00:00:00 | ||
图片预览

文档简介
牙林一中2012-2013学年高二上学期期中考试数学(文)试题
一.选择题(125分=60分)
1. 一个年级有12个班,每个班的同学从1至50排学号,为了交流学习经验,要求每班学号为14的同学留下进行交流,这里运用的是
A.分层抽样 B.抽签抽样 C.随机抽样 D.系统抽样
2.若函数的定义域是,则函数的定义域是
A. B. C. D.
3. 命题“若,则”的逆否命题是
A.若,则或 B.若,则
C.若或,则 D.若或,则
4. 不等式(a-2)x2+2(a-2)x-4<0,对一切?x∈R恒成立,则a的取值范围是
A.(-∞,2] B.(-2,2] C.(-2,2) D.(-∞,2)
5. 如果执行右面的程序框图,那么输出的
A.22 B.46 C. D.190
6. 抛掷三枚均匀的硬币,出现一枚正面,二枚反面的概率等于
A、 B、 C、 D、
7. 不等式||>1的解集是
A.{x|x>1} B.{x|x<}
C.{x|8.若不等式x2+ax+1≥0对于一切x∈成立,则a的取值范围是
A.a≥0 B.a≥-2 C.a≥- D.a≥-3
9. 下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量(吨)与相应的生产能耗(吨)的几组对应数据:
3
4
5
6
2.5
4
4.5
根据上表提供的数据,求出关于的线性回归方程为,那么表中的值为
A. 3 B. 3.15 C. 3.5 D. 4.5
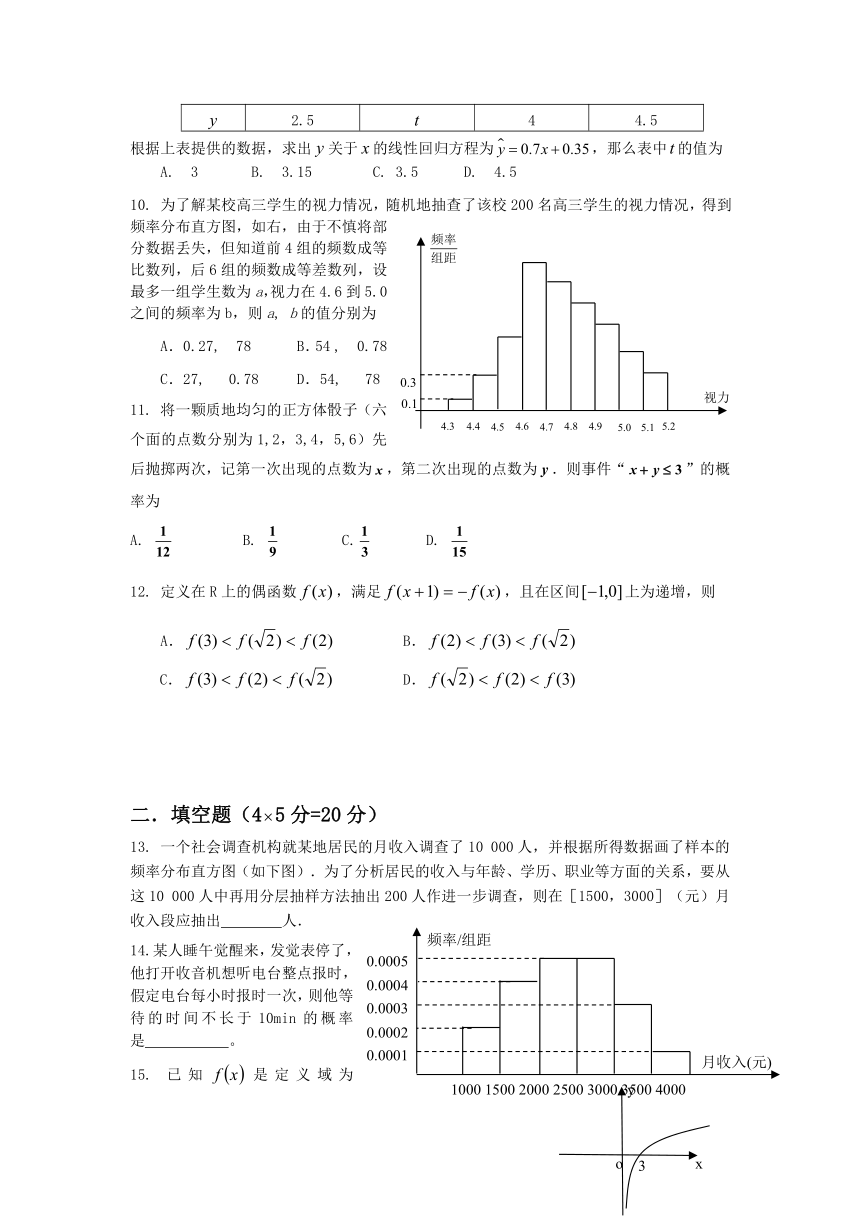
10. 为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a,视力在4.6到5.0之间的频率为b,则a, b的值分别为
A.0.27, 78 B.54 , 0.78
C.27, 0.78 D.54, 78
11. 将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为,第二次出现的点数为.则事件“”的概率为
A. B. C. D.
12. 定义在R上的偶函数,满足,且在区间上为递增,则
A. B.
C. D.
二.填空题(45分=20分)
13. 一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出200人作进一步调查,则在[1500,3000](元)月收入段应抽出 人.
14.某人睡午觉醒来,发觉表停了,他打开收音机想听电台整点报时,假定电台每小时报时一次,则他等待的时间不长于10min的概率是 。
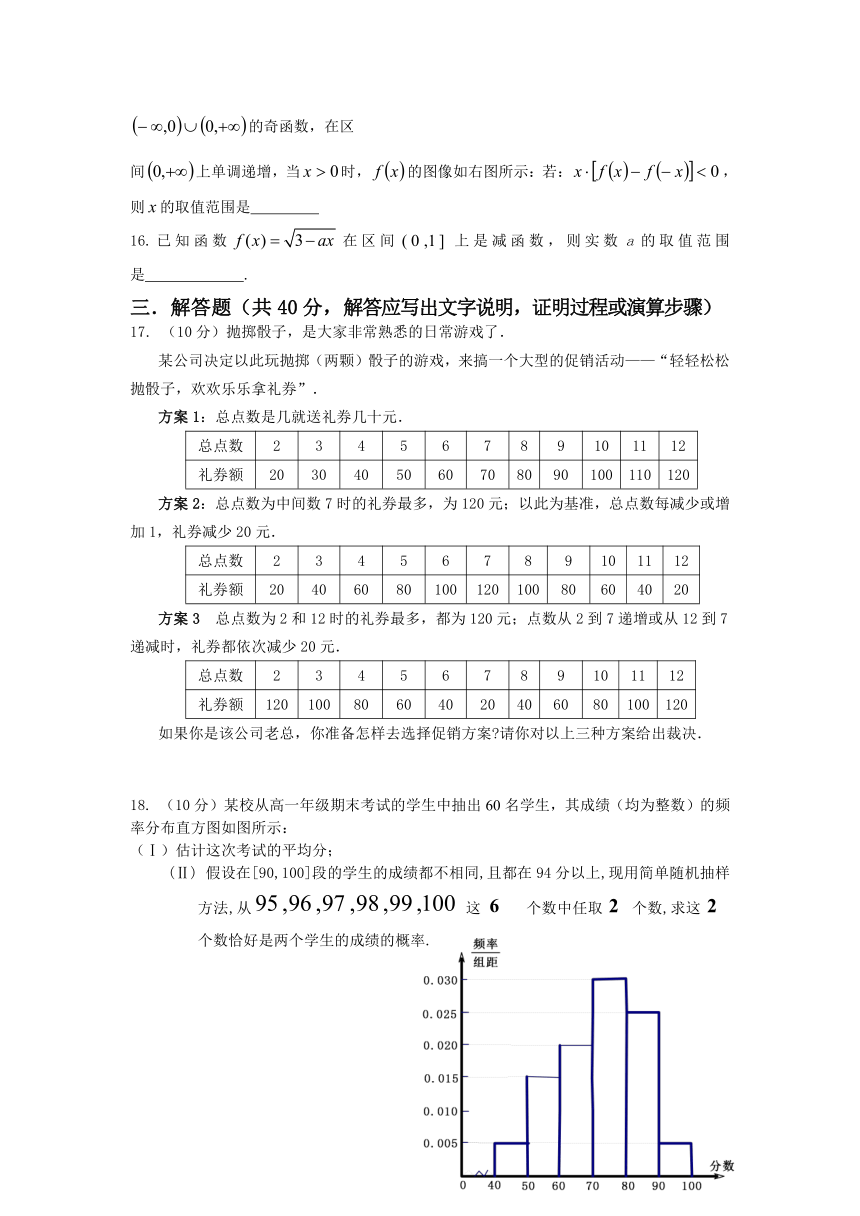
15. 已知是定义域为的奇函数,在区
间上单调递增,当时,的图像如右图所示:若:,则的取值范围是
16.已知函数在区间上是减函数,则实数a的取值范围是 .
三.解答题(共40分,解答应写出文字说明,证明过程或演算步骤)
17. (10分)抛掷骰子,是大家非常熟悉的日常游戏了.
某公司决定以此玩抛掷(两颗)骰子的游戏,来搞一个大型的促销活动——“轻轻松松抛骰子,欢欢乐乐拿礼券”.
方案1:总点数是几就送礼券几十元.
总点数
2
3
4
5
6
7
8
9
10
11
12
礼券额
20
30
40
50
60
70
80
90
100
110
120
方案2:总点数为中间数7时的礼券最多,为120元;以此为基准,总点数每减少或增加1,礼券减少20元.
总点数
2
3
4
5
6
7
8
9
10
11
12
礼券额
20
40
60
80
100
120
100
80
60
40
20
方案3 总点数为2和12时的礼券最多,都为120元;点数从2到7递增或从12到7递减时,礼券都依次减少20元.
总点数
2
3
4
5
6
7
8
9
10
11
12
礼券额
120
100
80
60
40
20
40
60
80
100
120
如果你是该公司老总,你准备怎样去选择促销方案?请你对以上三种方案给出裁决.
18. (10分)某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示:
(Ⅰ)估计这次考试的平均分;
(Ⅱ) 假设在[90,100]段的学生的成绩都不相同,且都在94分以上,现用简单随机抽样方法,从这个数中任取个数,求这个数恰好是两个学生的成绩的概率.
19. (10分)已知全集U=R,A={x|x2-2x-8<0},B={x||x+3|>2},C={x|x2-4ax+3a2<0}.
(1)C(A∩B),求a的取值范围;
(2)C(A)∩(B),求a的取值范围.
20. (10分) 已知,设命题P:不等式的解集是,命题Q:函数的定义域是。如果P或Q为真命题,P且Q为假命题,求的取值集合.
牙克石林业第一中学
2012--2013学年上学期高二年级期中考试
数 学 试 卷 (文)答 案
命题时间:2012年10月15日 命题人:陈海忠
三.解答题(共10分)
17. 最好选择方案3.表述基本正确就可给分。
由图可知,等可能基本事件总数为36种.
其中点数和为2的基本事件数为1个,点数和为3的基本事件数为2个,点数和为4的基本事件数为3个,点数和为5的基本事件数为4个,点数和为6的基本事件数为5个,点数和为7的基本事件数的和为6个,点数和为8的基本事件数为5个,点数和为9的基本事件数为4个,点数和为10的基本事件数为3个,点数和为11的基本事件数为2个,点数和为12的基本事件数为1个.
根据古典概型的概率计算公式易得下表:
点数和
2
3
4
5
6
7
8
9
10
11
12
概率
由概率可知,当点数和位于中间(指在7的附近)时,概率最大,作为追求最大效益与利润的老总,当然不能选择方案2,也不宜选择方案1,最好选择方案3.
另外,选择方案3,还有最大的一个优点那就是,它可造成视觉上与心理上的满足,顾客会认为最高奖(120元)可有两次机会,即点数和为2与12,中次最高奖(100元)也有两次机会,所以该方案是最可行的,事实上也一定是最促销的方案.
我们还可以从计算加以说明.三个方案中,均以抛掷36次为例加以计算(这是理论平均值):
点数和
2
3
4
5
6
7
8
9
10
11
12
合计所需
礼券额
点数和出现的次数
1
2
3
4
5
6
5
4
3
2
1
方案1礼券额
20
30
40
50
60
70
80
90
100
110
120
2520
方案1各点数和所需礼券额
20
60
120
200
300
420
400
360
300
220
120
方案2礼券额
20
40
60
80
100
120
100
80
60
40
20
2920
方案2各点数和所需礼券额
20
80
180
320
500
720
500
320
180
80
20
方案3礼券额
120
100
80
60
40
20
40
60
80
100
120
2120
方案3各点数和所需礼券额
120
200
240
240
200
120
200
240
240
200
120
从表清楚地看出,方案3所需的礼券额最少,对老总来说是应优先考虑的决策.
所以的范围为…………….6分
(2)(A)∩(B)=,要使C(A)∩(B)成立,只需
…………………………………………………………………………………………………10分
一.选择题(125分=60分)
1. 一个年级有12个班,每个班的同学从1至50排学号,为了交流学习经验,要求每班学号为14的同学留下进行交流,这里运用的是
A.分层抽样 B.抽签抽样 C.随机抽样 D.系统抽样
2.若函数的定义域是,则函数的定义域是
A. B. C. D.
3. 命题“若,则”的逆否命题是
A.若,则或 B.若,则
C.若或,则 D.若或,则
4. 不等式(a-2)x2+2(a-2)x-4<0,对一切?x∈R恒成立,则a的取值范围是
A.(-∞,2] B.(-2,2] C.(-2,2) D.(-∞,2)
5. 如果执行右面的程序框图,那么输出的
A.22 B.46 C. D.190
6. 抛掷三枚均匀的硬币,出现一枚正面,二枚反面的概率等于
A、 B、 C、 D、
7. 不等式||>1的解集是
A.{x|x>1} B.{x|x<}
C.{x|
A.a≥0 B.a≥-2 C.a≥- D.a≥-3
9. 下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量(吨)与相应的生产能耗(吨)的几组对应数据:
3
4
5
6
2.5
4
4.5
根据上表提供的数据,求出关于的线性回归方程为,那么表中的值为
A. 3 B. 3.15 C. 3.5 D. 4.5
10. 为了解某校高三学生的视力情况,随机地抽查了该校200名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最多一组学生数为a,视力在4.6到5.0之间的频率为b,则a, b的值分别为
A.0.27, 78 B.54 , 0.78
C.27, 0.78 D.54, 78
11. 将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为,第二次出现的点数为.则事件“”的概率为
A. B. C. D.
12. 定义在R上的偶函数,满足,且在区间上为递增,则
A. B.
C. D.
二.填空题(45分=20分)
13. 一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出200人作进一步调查,则在[1500,3000](元)月收入段应抽出 人.
14.某人睡午觉醒来,发觉表停了,他打开收音机想听电台整点报时,假定电台每小时报时一次,则他等待的时间不长于10min的概率是 。
15. 已知是定义域为的奇函数,在区
间上单调递增,当时,的图像如右图所示:若:,则的取值范围是
16.已知函数在区间上是减函数,则实数a的取值范围是 .
三.解答题(共40分,解答应写出文字说明,证明过程或演算步骤)
17. (10分)抛掷骰子,是大家非常熟悉的日常游戏了.
某公司决定以此玩抛掷(两颗)骰子的游戏,来搞一个大型的促销活动——“轻轻松松抛骰子,欢欢乐乐拿礼券”.
方案1:总点数是几就送礼券几十元.
总点数
2
3
4
5
6
7
8
9
10
11
12
礼券额
20
30
40
50
60
70
80
90
100
110
120
方案2:总点数为中间数7时的礼券最多,为120元;以此为基准,总点数每减少或增加1,礼券减少20元.
总点数
2
3
4
5
6
7
8
9
10
11
12
礼券额
20
40
60
80
100
120
100
80
60
40
20
方案3 总点数为2和12时的礼券最多,都为120元;点数从2到7递增或从12到7递减时,礼券都依次减少20元.
总点数
2
3
4
5
6
7
8
9
10
11
12
礼券额
120
100
80
60
40
20
40
60
80
100
120
如果你是该公司老总,你准备怎样去选择促销方案?请你对以上三种方案给出裁决.
18. (10分)某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示:
(Ⅰ)估计这次考试的平均分;
(Ⅱ) 假设在[90,100]段的学生的成绩都不相同,且都在94分以上,现用简单随机抽样方法,从这个数中任取个数,求这个数恰好是两个学生的成绩的概率.
19. (10分)已知全集U=R,A={x|x2-2x-8<0},B={x||x+3|>2},C={x|x2-4ax+3a2<0}.
(1)C(A∩B),求a的取值范围;
(2)C(A)∩(B),求a的取值范围.
20. (10分) 已知,设命题P:不等式的解集是,命题Q:函数的定义域是。如果P或Q为真命题,P且Q为假命题,求的取值集合.
牙克石林业第一中学
2012--2013学年上学期高二年级期中考试
数 学 试 卷 (文)答 案
命题时间:2012年10月15日 命题人:陈海忠
三.解答题(共10分)
17. 最好选择方案3.表述基本正确就可给分。
由图可知,等可能基本事件总数为36种.
其中点数和为2的基本事件数为1个,点数和为3的基本事件数为2个,点数和为4的基本事件数为3个,点数和为5的基本事件数为4个,点数和为6的基本事件数为5个,点数和为7的基本事件数的和为6个,点数和为8的基本事件数为5个,点数和为9的基本事件数为4个,点数和为10的基本事件数为3个,点数和为11的基本事件数为2个,点数和为12的基本事件数为1个.
根据古典概型的概率计算公式易得下表:
点数和
2
3
4
5
6
7
8
9
10
11
12
概率
由概率可知,当点数和位于中间(指在7的附近)时,概率最大,作为追求最大效益与利润的老总,当然不能选择方案2,也不宜选择方案1,最好选择方案3.
另外,选择方案3,还有最大的一个优点那就是,它可造成视觉上与心理上的满足,顾客会认为最高奖(120元)可有两次机会,即点数和为2与12,中次最高奖(100元)也有两次机会,所以该方案是最可行的,事实上也一定是最促销的方案.
我们还可以从计算加以说明.三个方案中,均以抛掷36次为例加以计算(这是理论平均值):
点数和
2
3
4
5
6
7
8
9
10
11
12
合计所需
礼券额
点数和出现的次数
1
2
3
4
5
6
5
4
3
2
1
方案1礼券额
20
30
40
50
60
70
80
90
100
110
120
2520
方案1各点数和所需礼券额
20
60
120
200
300
420
400
360
300
220
120
方案2礼券额
20
40
60
80
100
120
100
80
60
40
20
2920
方案2各点数和所需礼券额
20
80
180
320
500
720
500
320
180
80
20
方案3礼券额
120
100
80
60
40
20
40
60
80
100
120
2120
方案3各点数和所需礼券额
120
200
240
240
200
120
200
240
240
200
120
从表清楚地看出,方案3所需的礼券额最少,对老总来说是应优先考虑的决策.
所以的范围为…………….6分
(2)(A)∩(B)=,要使C(A)∩(B)成立,只需
…………………………………………………………………………………………………10分
同课章节目录
