人教A版(2019)必修 第一册 3.2探究与发现(双勾函数)教学设计
文档属性
| 名称 | 人教A版(2019)必修 第一册 3.2探究与发现(双勾函数)教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 252.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 16:51:56 | ||
图片预览


文档简介
3.3 探究函数的图象与性质
(人教A版普通高中教科书数学必修第一册第三章)
一、教学目标
1.能作出函数的图象
2.掌握函数的图象与性质
二、教学重难点
1.函数的图象与性质的探究过程
三、教学过程
1.1函数的引入
我们知道函数和都是幂函数,不同的函数通过加减乘除等运算可以构成新的函数,那么将这两个函数“相加”构成的函数有哪些性质呢?
1.2问题探究,形成规律
问题1 你认为可以从哪些方面研究函数?
【预设的答案】定义域、值域、奇偶性、单调性、最值、图象
【设计意图】研究一个函数应该研究什么?即研究一个函数应该从哪些方面入手.
问题2 你认为按照怎么的顺序去研究函数比较合适?
【预设的答案】应该先研究定义域、接着研究奇偶性、单调性、最值、值域、图象
【设计意图】应该先研究定义域,定义域优先原则,研究奇偶性可以事半功倍,研究单调性可以了解函数的增减趋势,为画图做好了准备,再结合最值、值域等可以画出函数的草图。
问题2.1 请写出函数的定义域,并判断函数奇偶性
【预设的答案】定义域为,为奇函数。
【设计意图】证明函数的奇偶性,要注意两步走应该先求定义域,看其是不是关于原点对称,接着求,若,则为奇函数;若,则为偶函数.
问题2.2求函数的单调区间?
【预设的答案】且
当时,
所以即且均有,所以函数的单调递减区间为;
当时,
所以即且均有所以函数的单调递增区间为;
综上函数的单调递减区间为;单调递增区间为.
【设计意图】考察学生用定义法证明单调性的过程,注意过程的规范性.
追问 你能写出函数的单调区间?
【预设的答案】由问题2.2以及函数奇偶性可知函数的单调递减区间为;单调递增区间为
【设计意图】体现出研究函数奇偶性的必要性,这样可以事半功倍.
问题2.3 求函数的最值
【预设的答案】当且仅当x=1时,函数最小值为2,无最大值.
【设计意图】考察学生利用基本不等式求最值的能力,利用基本不等式求最值,需要注意“一正,二定,三相等”.
追问 求函数的最值
【预设的答案】法1:当且仅当x=-1时,函数最大值为-2,无最小值.
法2:由问题2.3再结合函数奇偶性,可知当且仅当x=-1时,函数最大值为-2,无最小值.
【设计意图】一方面可以通过奇偶性(中心对称)得到,另一方面可通过基本不等式得到,仍然需要注意“一正,二定,三相等”.
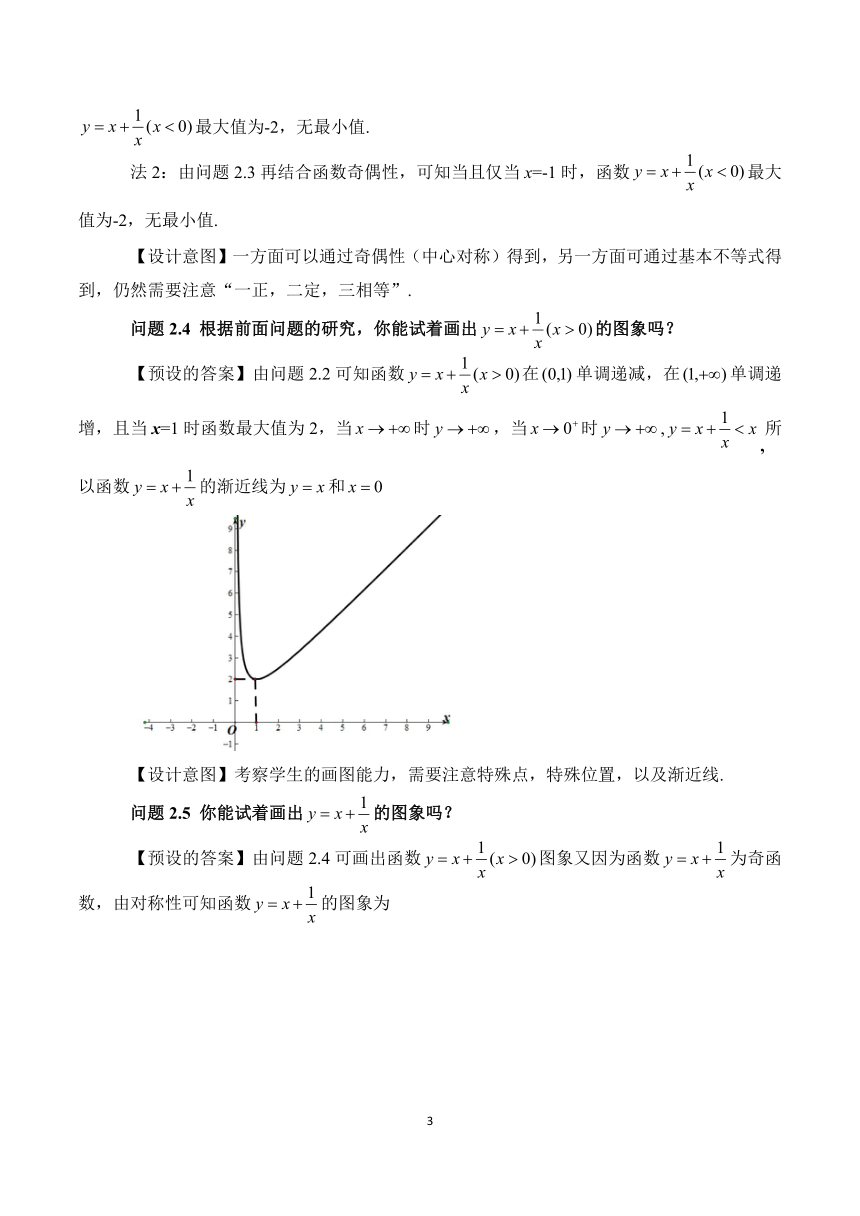
问题2.4 根据前面问题的研究,你能试着画出的图象吗?
【预设的答案】由问题2.2可知函数在单调递减,在单调递增,且当x=1时函数最大值为2,当时,当时,,所以函数的渐近线为和
【设计意图】考察学生的画图能力,需要注意特殊点,特殊位置,以及渐近线.
问题2.5 你能试着画出的图象吗?
【预设的答案】由问题2.4可画出函数图象又因为函数为奇函数,由对称性可知函数的图象为
【设计意图】再次体现出研究奇偶性的必要性“事半功倍”
追问 函数的图象像什么?能不能给它起个名字?
【预设的答案】像个对勾,“耐克”
【设计意图】用通俗易懂的名字给该函数命名,比如“双勾函数”“对勾函数”“耐克函数”加深学生的印象.
问题3 你能利用函数和的图象变化趋势说明一下函数的图象变化趋势吗?
【预设的答案】函数在均匀增长,而函数虽然也在递减但是在递减较快,在递减较慢,而函数和的通过叠加可得到函数图象,所以函数在递减,在递增,在结合三者在同一坐标系的图象可以更直观体现出这种关系.
【设计意图】函数和的与函数的联系.
1.3总结规律
问题4 通过对函数的图象与性质的研究,你有哪些体会?
【预设的答案】函数的三要素以及函数性质与图象是研究函数的主要方向,但是需要遵循一定的研究顺序,这样可以事半功倍,先确定函数的定义域,接着奇偶性,其次单调性最值,图象.
【设计意图】总结研究过程,形成经验.
1.4应用规律
问题5 你能试着研究函数的图象与性质吗?函数呢?请补充下列表格
函数
图象
定义域
值域
性质 奇偶性
单调性
最值
【预设的答案】
函数
图象
定义域
值域
性质 奇偶性 奇函数 奇函数 奇函数
单调性 单调递减区间: 单调递增区间: 无单调递减区间 单调递增区间: 单调递减区间: 单调递增区间:
最值 当时,当且仅当函数的最小值为2,无最大值; 当时,当且仅当函数的最大值为,无最小值 无最值 当时,当且仅当函数的最小值为,无最大值; 当时,当且仅当函数的最大值为,无最小值
【设计意图】应用探究所形成的经验,解决问题.
2
(人教A版普通高中教科书数学必修第一册第三章)
一、教学目标
1.能作出函数的图象
2.掌握函数的图象与性质
二、教学重难点
1.函数的图象与性质的探究过程
三、教学过程
1.1函数的引入
我们知道函数和都是幂函数,不同的函数通过加减乘除等运算可以构成新的函数,那么将这两个函数“相加”构成的函数有哪些性质呢?
1.2问题探究,形成规律
问题1 你认为可以从哪些方面研究函数?
【预设的答案】定义域、值域、奇偶性、单调性、最值、图象
【设计意图】研究一个函数应该研究什么?即研究一个函数应该从哪些方面入手.
问题2 你认为按照怎么的顺序去研究函数比较合适?
【预设的答案】应该先研究定义域、接着研究奇偶性、单调性、最值、值域、图象
【设计意图】应该先研究定义域,定义域优先原则,研究奇偶性可以事半功倍,研究单调性可以了解函数的增减趋势,为画图做好了准备,再结合最值、值域等可以画出函数的草图。
问题2.1 请写出函数的定义域,并判断函数奇偶性
【预设的答案】定义域为,为奇函数。
【设计意图】证明函数的奇偶性,要注意两步走应该先求定义域,看其是不是关于原点对称,接着求,若,则为奇函数;若,则为偶函数.
问题2.2求函数的单调区间?
【预设的答案】且
当时,
所以即且均有,所以函数的单调递减区间为;
当时,
所以即且均有所以函数的单调递增区间为;
综上函数的单调递减区间为;单调递增区间为.
【设计意图】考察学生用定义法证明单调性的过程,注意过程的规范性.
追问 你能写出函数的单调区间?
【预设的答案】由问题2.2以及函数奇偶性可知函数的单调递减区间为;单调递增区间为
【设计意图】体现出研究函数奇偶性的必要性,这样可以事半功倍.
问题2.3 求函数的最值
【预设的答案】当且仅当x=1时,函数最小值为2,无最大值.
【设计意图】考察学生利用基本不等式求最值的能力,利用基本不等式求最值,需要注意“一正,二定,三相等”.
追问 求函数的最值
【预设的答案】法1:当且仅当x=-1时,函数最大值为-2,无最小值.
法2:由问题2.3再结合函数奇偶性,可知当且仅当x=-1时,函数最大值为-2,无最小值.
【设计意图】一方面可以通过奇偶性(中心对称)得到,另一方面可通过基本不等式得到,仍然需要注意“一正,二定,三相等”.
问题2.4 根据前面问题的研究,你能试着画出的图象吗?
【预设的答案】由问题2.2可知函数在单调递减,在单调递增,且当x=1时函数最大值为2,当时,当时,,所以函数的渐近线为和
【设计意图】考察学生的画图能力,需要注意特殊点,特殊位置,以及渐近线.
问题2.5 你能试着画出的图象吗?
【预设的答案】由问题2.4可画出函数图象又因为函数为奇函数,由对称性可知函数的图象为
【设计意图】再次体现出研究奇偶性的必要性“事半功倍”
追问 函数的图象像什么?能不能给它起个名字?
【预设的答案】像个对勾,“耐克”
【设计意图】用通俗易懂的名字给该函数命名,比如“双勾函数”“对勾函数”“耐克函数”加深学生的印象.
问题3 你能利用函数和的图象变化趋势说明一下函数的图象变化趋势吗?
【预设的答案】函数在均匀增长,而函数虽然也在递减但是在递减较快,在递减较慢,而函数和的通过叠加可得到函数图象,所以函数在递减,在递增,在结合三者在同一坐标系的图象可以更直观体现出这种关系.
【设计意图】函数和的与函数的联系.
1.3总结规律
问题4 通过对函数的图象与性质的研究,你有哪些体会?
【预设的答案】函数的三要素以及函数性质与图象是研究函数的主要方向,但是需要遵循一定的研究顺序,这样可以事半功倍,先确定函数的定义域,接着奇偶性,其次单调性最值,图象.
【设计意图】总结研究过程,形成经验.
1.4应用规律
问题5 你能试着研究函数的图象与性质吗?函数呢?请补充下列表格
函数
图象
定义域
值域
性质 奇偶性
单调性
最值
【预设的答案】
函数
图象
定义域
值域
性质 奇偶性 奇函数 奇函数 奇函数
单调性 单调递减区间: 单调递增区间: 无单调递减区间 单调递增区间: 单调递减区间: 单调递增区间:
最值 当时,当且仅当函数的最小值为2,无最大值; 当时,当且仅当函数的最大值为,无最小值 无最值 当时,当且仅当函数的最小值为,无最大值; 当时,当且仅当函数的最大值为,无最小值
【设计意图】应用探究所形成的经验,解决问题.
2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
