华东师大版数学七年级上册 第2章 有理数2.10 有理数的除法课件(共20张PPT)
文档属性
| 名称 | 华东师大版数学七年级上册 第2章 有理数2.10 有理数的除法课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
有理数的除法
1.了解有理数除法的意义,理解有理数倒数的意义.
2.掌握有理数除法法则,能熟练地进行有理数除法运算.
有理数的乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与零相乘,都得零。
倒 数
- 与- 互为倒数,
例如,
-2与- 互为倒数,
-2.5与 互为倒数.
你能再举出几个互为倒数的数吗?
小学里我们学过倒数的定义,对有理数仍有:
乘积是1的两个数互为倒数。
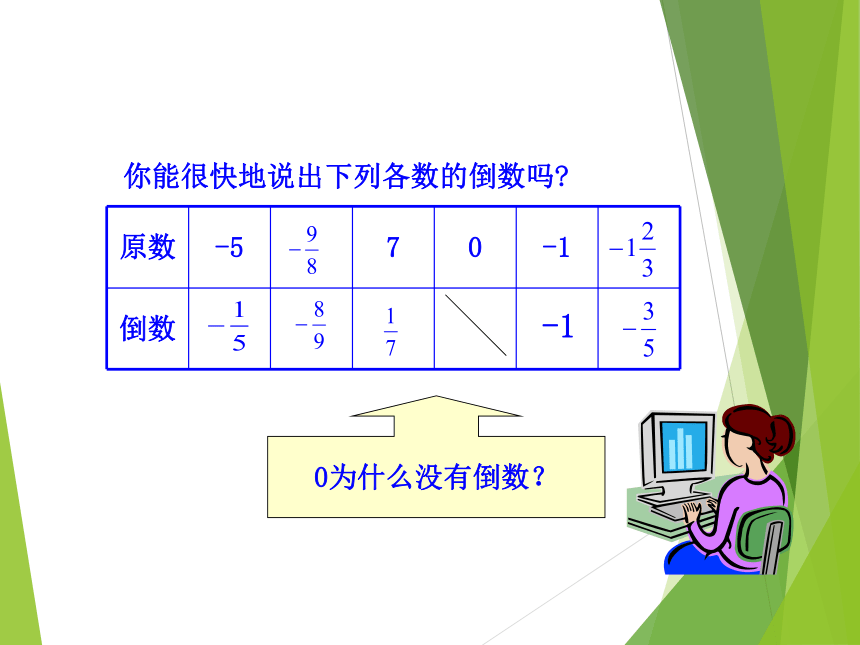
你能很快地说出下列各数的倒数吗
原数 -5 7 0 -1
倒数
-1
0为什么没有倒数?
2.讨论两数相除的例子有哪些情形?
思考:1.小学是怎样进行除法运算的?
正数除以正数
8÷4
负数除以正数
(-8)÷4
零除以正数
0÷4
正数除以负数
8÷(-4)
负数除以负数
(-8)÷(-4)
零除以负数
0÷(-4)
思考: 0能否做除数
正数除以正数
负数除以正数
零除以正数
8÷4
(-8)÷4
0÷4
=2
=-2
=0
=2
=-2
=0
除以一个正数等于乘以这个正数的倒数。
正数除以负数
负数除以负数
零除以负数
8÷(-4)
(-8)÷(-4)
0÷(-4)
=-2
=2
=0
=-2
=2
=0
除以一个负数等于乘以这个负数的倒数。
有理数除法法则:
(1)除以一个数,等于乘以这个数的倒数.零不能作
除数.
a÷b=a· (b≠0).
(2)两数相除,同号得___,异号得___,并把绝对值相
____。零除以任何一个不等于零的数,都得___。
正
负
除
零
【例1】计算
【例题】
【例2】化简下列各式:
【例3】计算:
求下列各数的倒数:
(1)-3 (2) (3)0.2
分析:欲求某数的倒数,就是要确定与这个数相乘积
为1的数是什么。
【跟踪训练】
解:(1) 因为(-3)×(- )=1,
所以-3的倒数是-
(2)因为- 1 =- ,- =1,
所以-1 的倒数是- .
(3)因为0.2= = ,
×5=1,所以 0.2的倒数是5
×
注意:
求小数的倒数时,要先把小数化成分数;
求带分数的倒数时,要先把带分数化成假分数。
1.计算:(-6)÷(-2)=_____.
【解析】(-6)÷(-2)=6÷2=3.
答案:3
2.(怀化·中考)下列运算结果等于1的是( )
A.(-3)+(-3) B.(-3)-(-3)
C.(-3)×(-3) D.(-3)÷(-3)
【解析】选D. A选项结果等于-6,B选项结果等于0,C选项结果等于9,D选项结果等于1。
3.如果两个有理数的商等于0,则( )。
A.两个数中有一个数为0 B.两数都为0
C.被除数为0,除数不为0 D.被除数不为0,除数为0
【解析】选C.0除以任何不等于0的数都得0,0不能作除数。
(4)( )÷( )
(5)(-6.5)÷0.13
4.计算
(1)1÷(-9)
(2)0÷(-8)
(3)16÷(-3)
=0
=-50
一、有理数的除法法则(一)
除以一个数等于乘以这个数的倒数。
即a÷b=a· (b≠0)。
二、有理数的除法法则(二)
两数相除,同号得正,异号得负,并把绝对值相除。
零除以任何一个不等于零的数,都得零。
三、注意:
1.零不能作除数
2.一般在不能整除的情况下应用第一法则,在能整除的情况 下应用第二法则。
凡事顺其自然,遇事处之泰然,得意之时淡然,失意之时坦然,艰辛曲折必然,历尽沧桑悟然。
有理数的除法
1.了解有理数除法的意义,理解有理数倒数的意义.
2.掌握有理数除法法则,能熟练地进行有理数除法运算.
有理数的乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数与零相乘,都得零。
倒 数
- 与- 互为倒数,
例如,
-2与- 互为倒数,
-2.5与 互为倒数.
你能再举出几个互为倒数的数吗?
小学里我们学过倒数的定义,对有理数仍有:
乘积是1的两个数互为倒数。
你能很快地说出下列各数的倒数吗
原数 -5 7 0 -1
倒数
-1
0为什么没有倒数?
2.讨论两数相除的例子有哪些情形?
思考:1.小学是怎样进行除法运算的?
正数除以正数
8÷4
负数除以正数
(-8)÷4
零除以正数
0÷4
正数除以负数
8÷(-4)
负数除以负数
(-8)÷(-4)
零除以负数
0÷(-4)
思考: 0能否做除数
正数除以正数
负数除以正数
零除以正数
8÷4
(-8)÷4
0÷4
=2
=-2
=0
=2
=-2
=0
除以一个正数等于乘以这个正数的倒数。
正数除以负数
负数除以负数
零除以负数
8÷(-4)
(-8)÷(-4)
0÷(-4)
=-2
=2
=0
=-2
=2
=0
除以一个负数等于乘以这个负数的倒数。
有理数除法法则:
(1)除以一个数,等于乘以这个数的倒数.零不能作
除数.
a÷b=a· (b≠0).
(2)两数相除,同号得___,异号得___,并把绝对值相
____。零除以任何一个不等于零的数,都得___。
正
负
除
零
【例1】计算
【例题】
【例2】化简下列各式:
【例3】计算:
求下列各数的倒数:
(1)-3 (2) (3)0.2
分析:欲求某数的倒数,就是要确定与这个数相乘积
为1的数是什么。
【跟踪训练】
解:(1) 因为(-3)×(- )=1,
所以-3的倒数是-
(2)因为- 1 =- ,- =1,
所以-1 的倒数是- .
(3)因为0.2= = ,
×5=1,所以 0.2的倒数是5
×
注意:
求小数的倒数时,要先把小数化成分数;
求带分数的倒数时,要先把带分数化成假分数。
1.计算:(-6)÷(-2)=_____.
【解析】(-6)÷(-2)=6÷2=3.
答案:3
2.(怀化·中考)下列运算结果等于1的是( )
A.(-3)+(-3) B.(-3)-(-3)
C.(-3)×(-3) D.(-3)÷(-3)
【解析】选D. A选项结果等于-6,B选项结果等于0,C选项结果等于9,D选项结果等于1。
3.如果两个有理数的商等于0,则( )。
A.两个数中有一个数为0 B.两数都为0
C.被除数为0,除数不为0 D.被除数不为0,除数为0
【解析】选C.0除以任何不等于0的数都得0,0不能作除数。
(4)( )÷( )
(5)(-6.5)÷0.13
4.计算
(1)1÷(-9)
(2)0÷(-8)
(3)16÷(-3)
=0
=-50
一、有理数的除法法则(一)
除以一个数等于乘以这个数的倒数。
即a÷b=a· (b≠0)。
二、有理数的除法法则(二)
两数相除,同号得正,异号得负,并把绝对值相除。
零除以任何一个不等于零的数,都得零。
三、注意:
1.零不能作除数
2.一般在不能整除的情况下应用第一法则,在能整除的情况 下应用第二法则。
凡事顺其自然,遇事处之泰然,得意之时淡然,失意之时坦然,艰辛曲折必然,历尽沧桑悟然。
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
