沪科版数学八年级上册 15.3 等腰三角形 课件(共17张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 15.3 等腰三角形 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 896.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 08:24:40 | ||
图片预览



文档简介
(共17张PPT)
15.3 等腰三角形
下载图片
等腰三角形
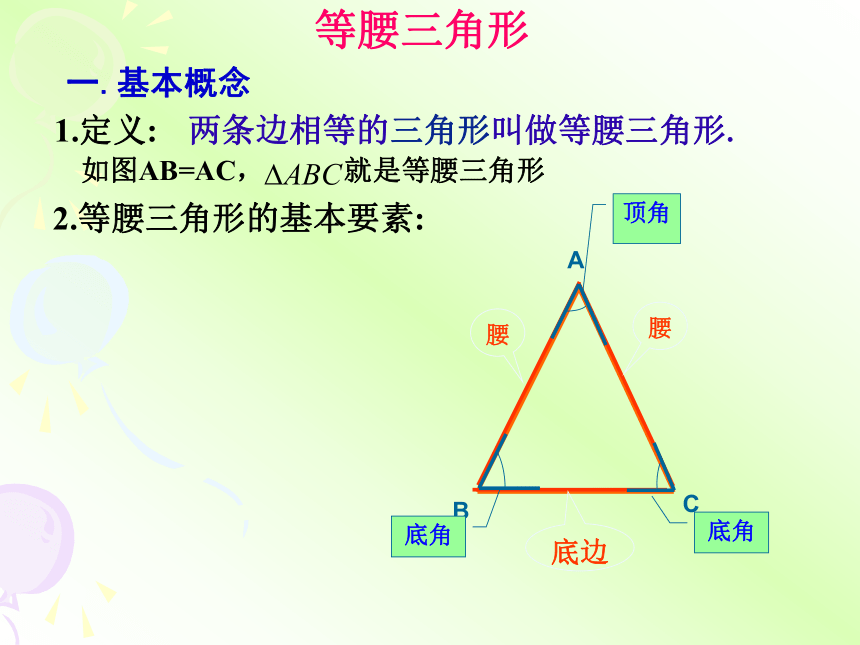
一.基本概念
1.定义:
两条边相等的三角形叫做等腰三角形.
如图AB=AC, 就是等腰三角形
2.等腰三角形的基本要素:
A
B
C
腰
腰
底边
顶角
底角
底角
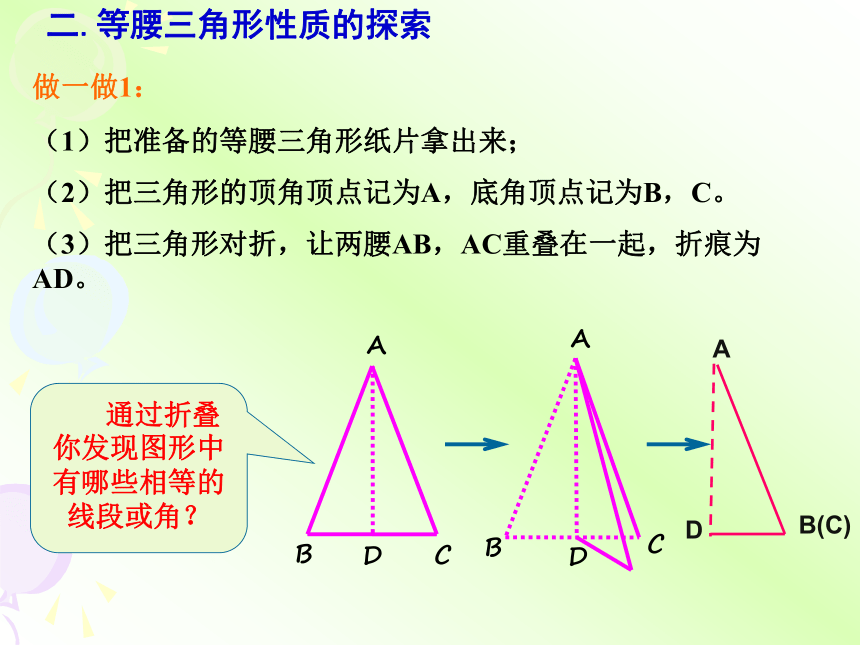
做一做1:
(1)把准备的等腰三角形纸片拿出来;
(2)把三角形的顶角顶点记为A,底角顶点记为B,C。
(3)把三角形对折,让两腰AB,AC重叠在一起,折痕为AD。
二.等腰三角形性质的探索
B
A
C
D
A
B
C
D
A
B(C)
D
通过折叠你发现图形中有哪些相等的线段或角?
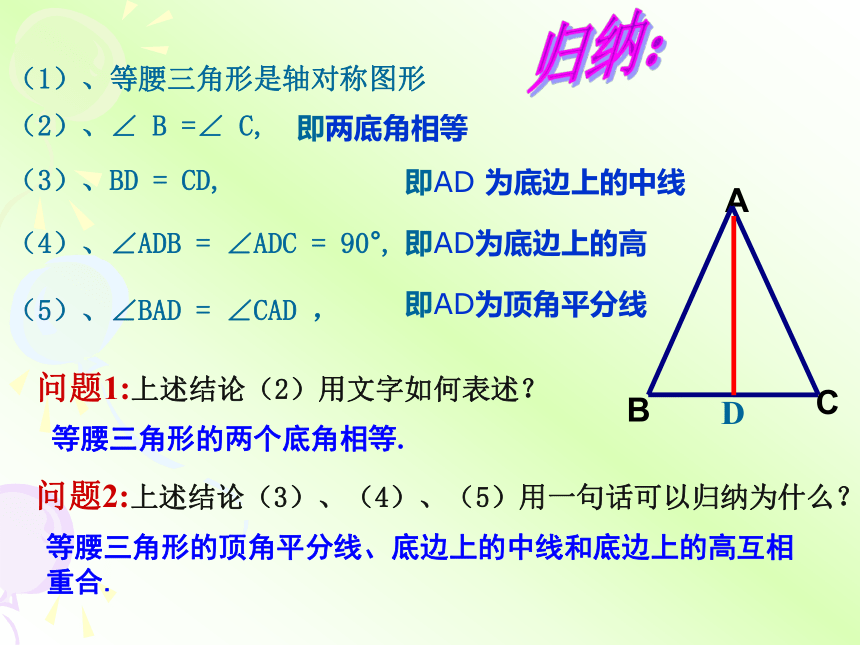
(1)、等腰三角形是轴对称图形
(2)、∠ B =∠ C,
(3)、BD = CD,
(4)、∠ADB = ∠ADC = 90°,
(5)、∠BAD = ∠CAD ,
C
A
B
D
问题1:上述结论(2)用文字如何表述?
等腰三角形的两个底角相等.
问题2:上述结论(3)、(4)、(5)用一句话可以归纳为什么?
等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合.
即两底角相等
即AD 为底边上的中线
即AD为底边上的高
即AD为顶角平分线
C
A
B
D
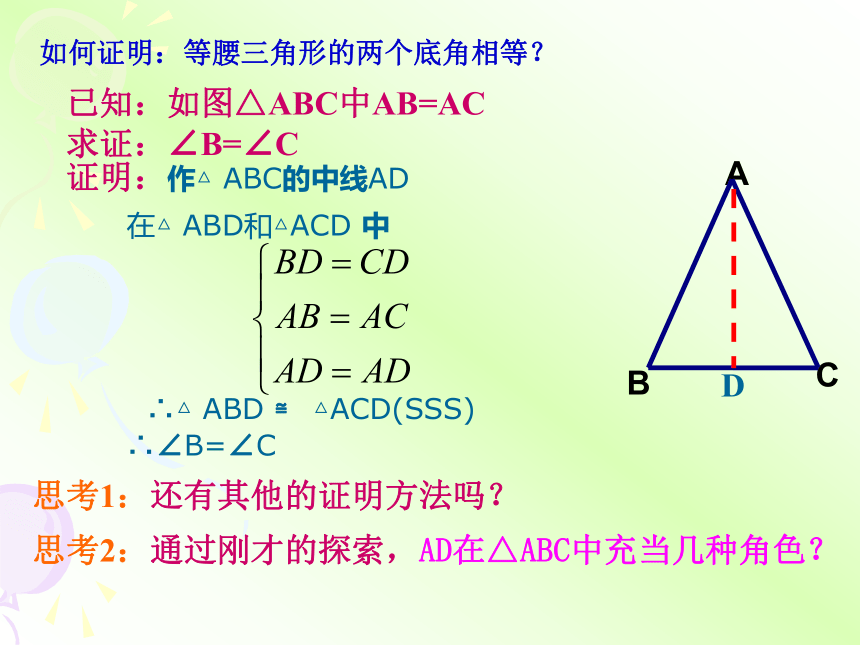
如何证明:等腰三角形的两个底角相等?
已知:如图△ABC中AB=AC
求证:∠B=∠C
证明:作△ ABC的中线AD
在△ ABD和△ACD 中
∴△ ABD ≌ △ACD(SSS)
∴∠B=∠C
思考1:还有其他的证明方法吗?
思考2:通过刚才的探索,AD在△ABC中充当几种角色?
等腰三角形的性质
1、等腰三角形的两个底角相等
(简称“等边对等角”)
2、等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合。(简称“三线合一”)
一般的三角形有这种性质吗?
要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。
C
D
B
A
1、(1) 在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )
等边对等角
① ∵AD⊥BC,
∴∠____ = ∠____,___= ___
② ∵AD是中线,∴___⊥___ ,∠____ =∠____
③∵AD是角平分线,
∴___ ⊥___ ,___ =___
BAD CAD
BD CD
AD BC
AD BC
BAD CAD
BD CD
(2) 在△ABC中, AB=AC时,
课堂练习:
(三线合一)
2 、在△ ABC中,若AB=BC=CA,
则 ∠A=______
∠B=______
∠C=______
推论:
等边三角形三个内角都相等,每一个角都等于 。
课堂练习:
60 °
60 °
60 °
60°
解:∵ AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C= 30°
又∵BD=AD(已知)
∴∠BAD=∠B= 30°(等边对等角)
同理 ∠CAE =∠C= 30°
∴∠DAE =∠BAC-∠BAD-∠CAE
=120°-30°-30°
=60 °
例1: 如图在△ABC中,AB=AC,∠BAC=120°,点D、E是底边的两点,且BD=AD,CE=AE,
求∠DAE的度数。
A
B
C
D
E
能力拓展: 已知,如图AB=AC,AD=AE。求证:BD=CE。
E
D
C
B
A
方法一:
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
同理:∠ADE=∠AED
又∵ ∠ADE+∠ADB=180°
∠AED+∠AEC=180 °
∠ADB=∠AEC(等角的补角相等)
在△ABD与△ ACD中
∵ ∠B=∠C
∠ADB=∠AEC
AD=AE
∴ △ ABD≌ △ ACE(AAS)
∴ BD=CE
方法二:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CE
F
∟
方法三:
证明△ ABE≌ △ ACD
⒈等腰三角形一个底角为40°,它的顶角为______.
⒉等腰三角形一顶角为40°,它的另外两个底角为
__________________.
⒊等腰三角形一个角为40°,它的另外两个角为___________.
100 °
100°,40 °
或70 °,70 °
70°,70°
4.等腰三角形一个角为120°,它的另外两个角为 .
30°30°
1、等腰三角形的性质:
等边对等角
2、 等腰三角形顶角的平分线垂直平分底边(三线合一)
4、有时利用等腰三角形的“三线合一”性质作辅助线(顶角的平分线、底边上的高、底边上的中线),可帮助我们解决实际问题。
3、等边三角形三个内角相等,每一个内角都等于60°
布置作业
课本P126页练习第2题、习题16.3第7题
挑战题:已知,如图△ABC是等边三角形,AE平分∠BAC交BC于E,以BE为边向△ABC的外部作等边△BED。
求证:BD⊥CD
A
B
C
D
E
再 见!
15.3 等腰三角形
下载图片
等腰三角形
一.基本概念
1.定义:
两条边相等的三角形叫做等腰三角形.
如图AB=AC, 就是等腰三角形
2.等腰三角形的基本要素:
A
B
C
腰
腰
底边
顶角
底角
底角
做一做1:
(1)把准备的等腰三角形纸片拿出来;
(2)把三角形的顶角顶点记为A,底角顶点记为B,C。
(3)把三角形对折,让两腰AB,AC重叠在一起,折痕为AD。
二.等腰三角形性质的探索
B
A
C
D
A
B
C
D
A
B(C)
D
通过折叠你发现图形中有哪些相等的线段或角?
(1)、等腰三角形是轴对称图形
(2)、∠ B =∠ C,
(3)、BD = CD,
(4)、∠ADB = ∠ADC = 90°,
(5)、∠BAD = ∠CAD ,
C
A
B
D
问题1:上述结论(2)用文字如何表述?
等腰三角形的两个底角相等.
问题2:上述结论(3)、(4)、(5)用一句话可以归纳为什么?
等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合.
即两底角相等
即AD 为底边上的中线
即AD为底边上的高
即AD为顶角平分线
C
A
B
D
如何证明:等腰三角形的两个底角相等?
已知:如图△ABC中AB=AC
求证:∠B=∠C
证明:作△ ABC的中线AD
在△ ABD和△ACD 中
∴△ ABD ≌ △ACD(SSS)
∴∠B=∠C
思考1:还有其他的证明方法吗?
思考2:通过刚才的探索,AD在△ABC中充当几种角色?
等腰三角形的性质
1、等腰三角形的两个底角相等
(简称“等边对等角”)
2、等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合。(简称“三线合一”)
一般的三角形有这种性质吗?
要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。
C
D
B
A
1、(1) 在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )
等边对等角
① ∵AD⊥BC,
∴∠____ = ∠____,___= ___
② ∵AD是中线,∴___⊥___ ,∠____ =∠____
③∵AD是角平分线,
∴___ ⊥___ ,___ =___
BAD CAD
BD CD
AD BC
AD BC
BAD CAD
BD CD
(2) 在△ABC中, AB=AC时,
课堂练习:
(三线合一)
2 、在△ ABC中,若AB=BC=CA,
则 ∠A=______
∠B=______
∠C=______
推论:
等边三角形三个内角都相等,每一个角都等于 。
课堂练习:
60 °
60 °
60 °
60°
解:∵ AB=AC(已知)
∴∠B=∠C(等边对等角)
∴∠B=∠C= 30°
又∵BD=AD(已知)
∴∠BAD=∠B= 30°(等边对等角)
同理 ∠CAE =∠C= 30°
∴∠DAE =∠BAC-∠BAD-∠CAE
=120°-30°-30°
=60 °
例1: 如图在△ABC中,AB=AC,∠BAC=120°,点D、E是底边的两点,且BD=AD,CE=AE,
求∠DAE的度数。
A
B
C
D
E
能力拓展: 已知,如图AB=AC,AD=AE。求证:BD=CE。
E
D
C
B
A
方法一:
证明: ∵AB=AC
∴∠B=∠C(等边对等角)
同理:∠ADE=∠AED
又∵ ∠ADE+∠ADB=180°
∠AED+∠AEC=180 °
∠ADB=∠AEC(等角的补角相等)
在△ABD与△ ACD中
∵ ∠B=∠C
∠ADB=∠AEC
AD=AE
∴ △ ABD≌ △ ACE(AAS)
∴ BD=CE
方法二:
过A作AF⊥BC垂足为F点,
∵ AB=AC
∴BF=FC(三线合一)
同理:DF=EF
∴BF-DF=FC-EF
即BD=CE
F
∟
方法三:
证明△ ABE≌ △ ACD
⒈等腰三角形一个底角为40°,它的顶角为______.
⒉等腰三角形一顶角为40°,它的另外两个底角为
__________________.
⒊等腰三角形一个角为40°,它的另外两个角为___________.
100 °
100°,40 °
或70 °,70 °
70°,70°
4.等腰三角形一个角为120°,它的另外两个角为 .
30°30°
1、等腰三角形的性质:
等边对等角
2、 等腰三角形顶角的平分线垂直平分底边(三线合一)
4、有时利用等腰三角形的“三线合一”性质作辅助线(顶角的平分线、底边上的高、底边上的中线),可帮助我们解决实际问题。
3、等边三角形三个内角相等,每一个内角都等于60°
布置作业
课本P126页练习第2题、习题16.3第7题
挑战题:已知,如图△ABC是等边三角形,AE平分∠BAC交BC于E,以BE为边向△ABC的外部作等边△BED。
求证:BD⊥CD
A
B
C
D
E
再 见!
