河北省2021-2022学年八年级上学期期中考试数学试题(word解析版)
文档属性
| 名称 | 河北省2021-2022学年八年级上学期期中考试数学试题(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 20:35:18 | ||
图片预览

文档简介
河北省2021-2022学年八年级上学期期中考试数学试题含解析
姓名:__________ 班级:__________考号:__________
一、选择题(共21题)
1、 在实数 , , 0 , , 0.070070007… (相令两个 7 之间 0 的个数逐次加 1 )中,无理数有( )
A . 2 个 B . 3 个 C . 4 个 D . 5 个
2、 气象台为了预报台风,首先要确定它的位置,下列说法中,能确定台风具体位置的是 ( )
A .西太平洋
B .距台湾 30 海里
C .东经 33° ,北纬 36°
D .台湾岛附近
3、 下列平面直角坐标系中的图象,不能表示 y 是 x 的函数的是( )
A . B .
C . D .
4、 下面说法中,正确的是( )
A .实数分为正实数和负实数 B .带根号的数都是无理数
C .无限不循环小数都是无理数 D .平方根等于本身的数是 1 和 0
5、 下列各组数中,互为相反数的一组是( ).
A . 2 与 B . 与 C . 与 D . 与
6、 各组数中,是勾股数的是( )
A . 9 , 16 , 25 B . 0.3 , 0.4 , 0.5 C . 1 , , 2 D . 8 , 15 , 17
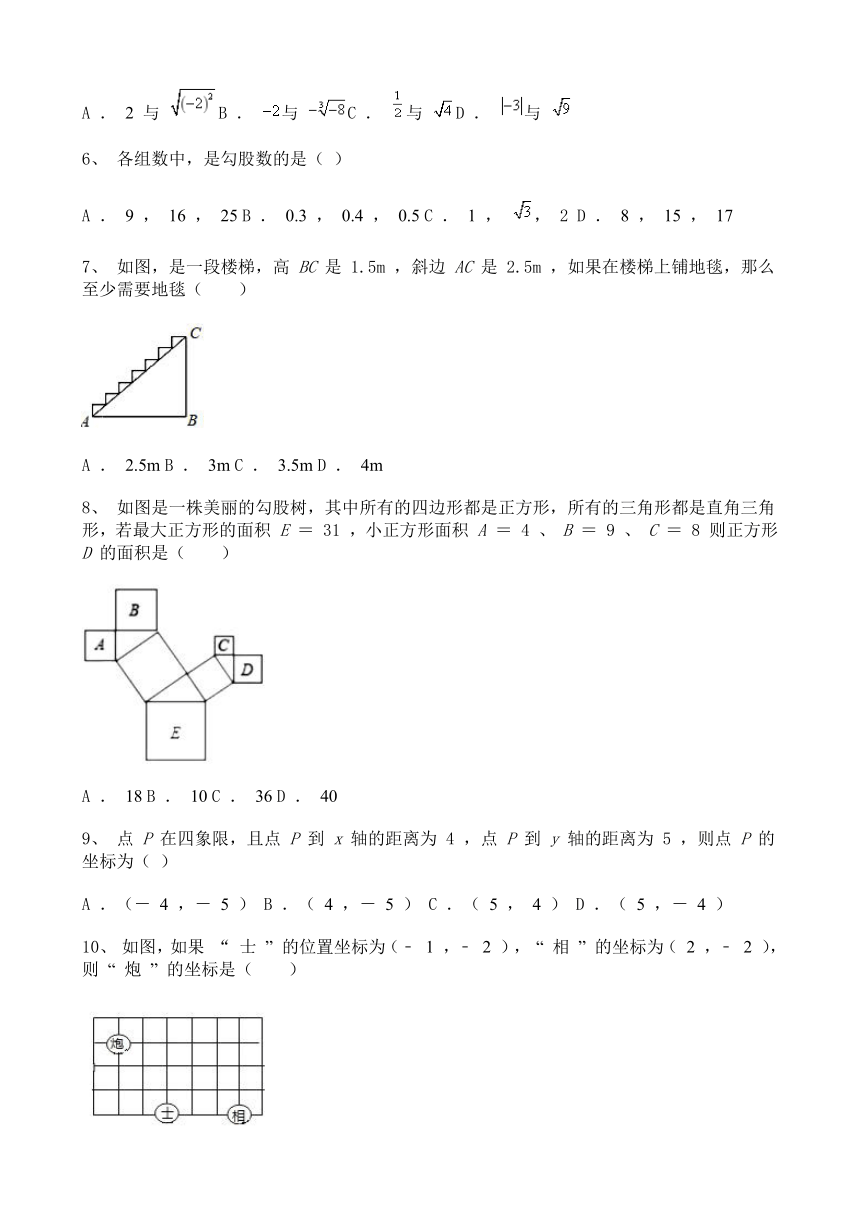
7、 如图,是一段楼梯,高 BC 是 1.5m ,斜边 AC 是 2.5m ,如果在楼梯上铺地毯,那么至少需要地毯( )
A . 2.5m B . 3m C . 3.5m D . 4m
8、 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若最大正方形的面积 E = 31 ,小正方形面积 A = 4 、 B = 9 、 C = 8 则正方形 D 的面积是( )
A . 18 B . 10 C . 36 D . 40
9、 点 P 在四象限,且点 P 到 x 轴的距离为 4 ,点 P 到 y 轴的距离为 5 ,则点 P 的坐标为( )
A .(- 4 ,- 5 ) B .( 4 ,- 5 ) C .( 5 , 4 ) D .( 5 ,- 4 )
10、 如图,如果 “ 士 ” 的位置坐标为(﹣ 1 ,﹣ 2 ), “ 相 ” 的坐标为( 2 ,﹣ 2 ),则 “ 炮 ” 的坐标是( )
A .(﹣ 3 , 1 ) B .( 1 ,﹣ 1 ) C .(﹣ 2 , 1 ) D .(﹣ 3 , 3 )
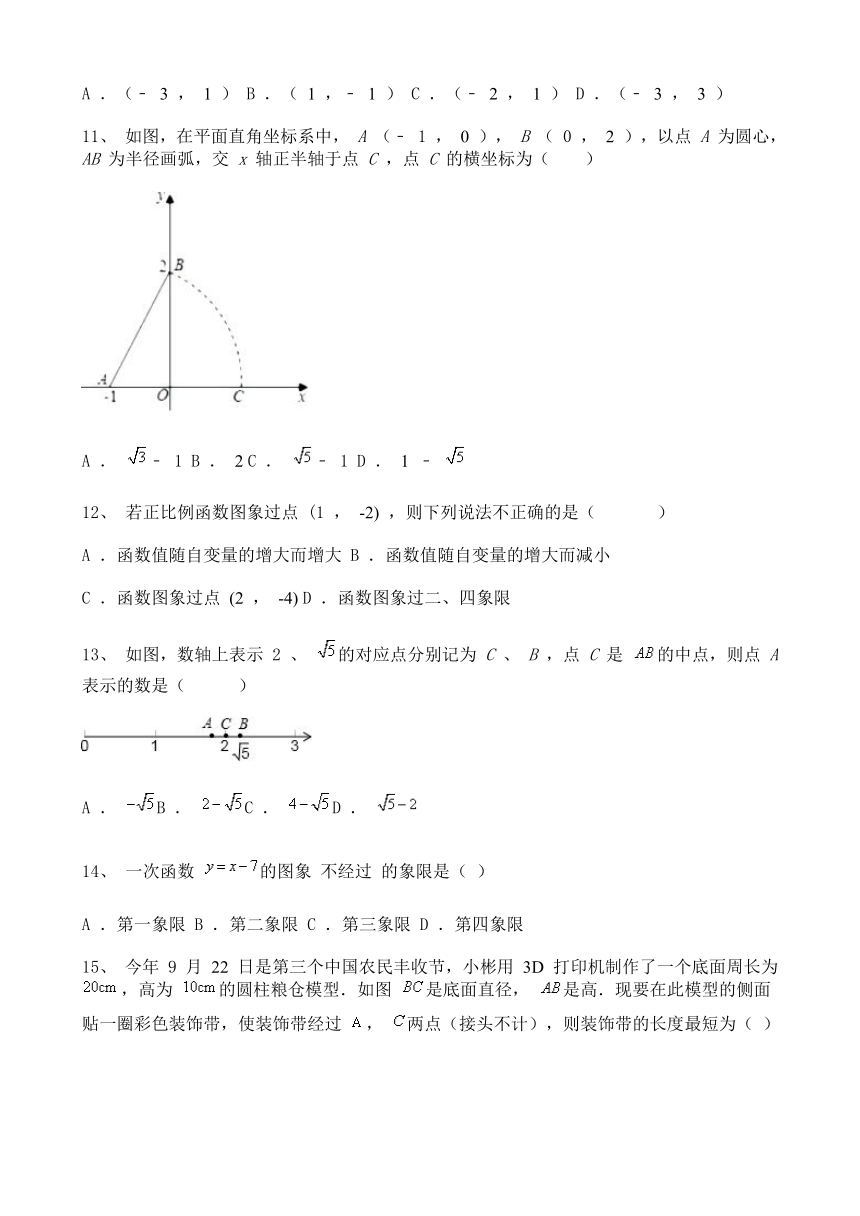
11、 如图,在平面直角坐标系中, A (﹣ 1 , 0 ), B ( 0 , 2 ),以点 A 为圆心, AB 为半径画弧,交 x 轴正半轴于点 C ,点 C 的横坐标为( )
A . ﹣ 1 B . 2 C . ﹣ 1 D . 1 ﹣
12、 若正比例函数图象过点 (1 , -2) ,则下列说法不正确的是( )
A .函数值随自变量的增大而增大 B .函数值随自变量的增大而减小
C .函数图象过点 (2 , -4) D .函数图象过二、四象限
13、 如图,数轴上表示 2 、 的对应点分别记为 C 、 B ,点 C 是 的中点,则点 A 表示的数是( )
A . B . C . D .
14、 一次函数 的图象 不经过 的象限是( )
A .第一象限 B .第二象限 C .第三象限 D .第四象限
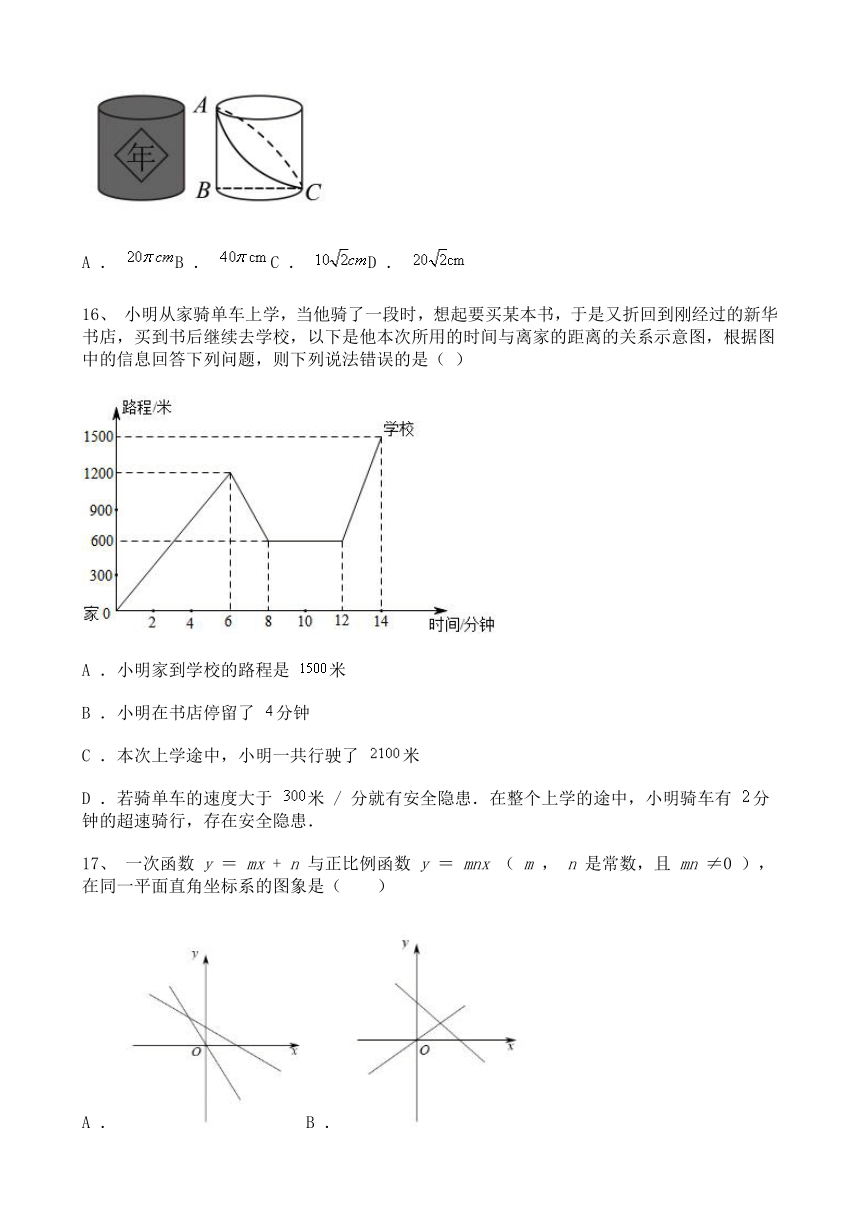
15、 今年 9 月 22 日是第三个中国农民丰收节,小彬用 3D 打印机制作了一个底面周长为 ,高为 的圆柱粮仓模型.如图 是底面直径, 是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过 , 两点(接头不计),则装饰带的长度最短为( )
A . B . C . D .
16、 小明从家骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与离家的距离的关系示意图,根据图中的信息回答下列问题,则下列说法错误的是( )
A .小明家到学校的路程是 米
B .小明在书店停留了 分钟
C .本次上学途中,小明一共行驶了 米
D .若骑单车的速度大于 米 / 分就有安全隐患.在整个上学的途中,小明骑车有 分钟的超速骑行,存在安全隐患.
17、 一次函数 y = mx + n 与正比例函数 y = mnx ( m , n 是常数,且 mn ≠0 ),在同一平面直角坐标系的图象是( )
A . B .
C . D .
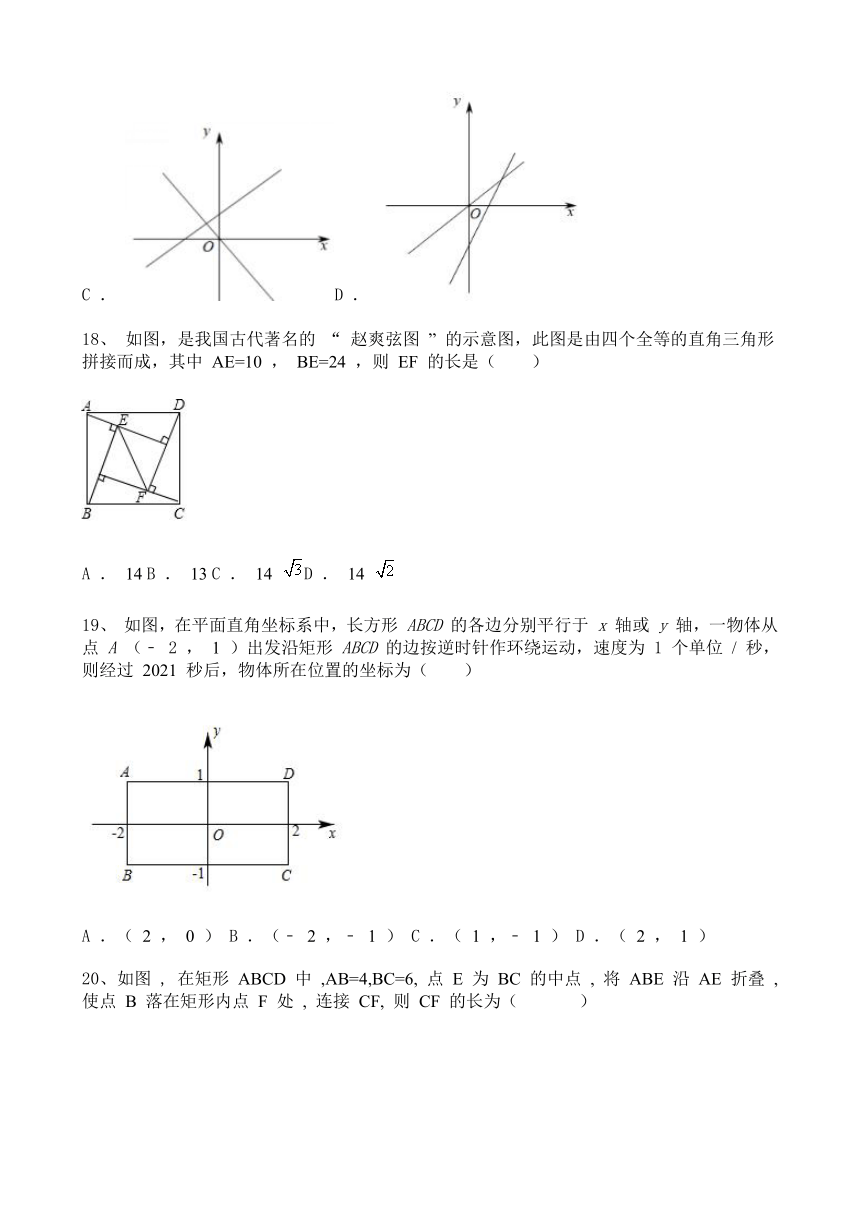
18、 如图,是我国古代著名的 “ 赵爽弦图 ” 的示意图,此图是由四个全等的直角三角形拼接而成,其中 AE=10 , BE=24 ,则 EF 的长是( )
A . 14 B . 13 C . 14 D . 14
19、 如图,在平面直角坐标系中,长方形 ABCD 的各边分别平行于 x 轴或 y 轴,一物体从点 A (﹣ 2 , 1 )出发沿矩形 ABCD 的边按逆时针作环绕运动,速度为 1 个单位 / 秒,则经过 2021 秒后,物体所在位置的坐标为( )
A .( 2 , 0 ) B .(﹣ 2 ,﹣ 1 ) C .( 1 ,﹣ 1 ) D .( 2 , 1 )
20、 如图 , 在矩形 ABCD 中 ,AB=4,BC=6, 点 E 为 BC 的中点 , 将 ABE 沿 AE 折叠 , 使点 B 落在矩形内点 F 处 , 连接 CF, 则 CF 的长为( )
A . B . C . D .
21、 如图,在平面直角坐标系中有一个 3×3 的正方形网格,其右下角格点(小正方形的顶点) A 的坐标为(﹣ 1 , 1 ),左上角格点 B 的坐标为(﹣ 4 , 4 ),若分布在过定点(﹣ 1 , 0 )的直线 y =﹣ k ( x +1 )两侧的格点数相同,则 k 的取值可以是( )
A . B . 2 C . D .
二、填空题(共9题)
1、 把直线 y=2x 向上平移 3 个单位得到直线 _____ .
2、 比较大小: ______ .
3、 已知函数 ( 为常数),当 ____________ 时, 是 的正比例函数 .
4、 若 .则 的立方根是 ___ .
5、 已知点 A 的坐标为( 1 , 2 ),直线 AB ∥ x 轴,且 AB = 5 ,则点 B 坐标为 _______________ .
6、 点 A ( x 1 , y 1 )和 B ( x 2 , y 2 )都在直线 y =﹣ 3 x +2 上,且 x 1 < x 2 ,则 y 1 ___ y 2 .
7、 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》: “ 平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地 …” 翻译成现代文为:如图,秋千 OA 静止的时候,踏板离地高一尺( 尺),将它往前推进两步( 尺),此时踏板升高离地五尺( 尺),则秋千绳索( OA 或 OB )的长度为 ______ 尺.
8、 如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点 , , , , , … ,则 的坐标是 ________ .
9、 “ 一把钥匙一把锁 ” ,请运用数学思维破译 “ 密码 ” ,小王同学目前已破译出 “ 今天考试 ” 的真实意思是 “ 努力发挥 ” ,那么破译 “ 正做数学 ” 的真实意思是 ________________ .
三、解答题(共8题)
1、 计算:
( 1 )
( 2 )
( 3 )
( 4 )
( 5 ) .
( 6 )求满足 x 的值:( x ﹣ 1 ) 2 = 2 .
2、 求代数式 a + 的值,其中 a = 1007 ,如图是小亮和小芳的解答过程.
( 1 ) 的解法是错误的;
( 2 )错误的原因在于未能正确的运用二次根式的性质: ;
( 3 )求代数式 a +2 的值,其中 a =﹣ 2022 .
3、 如图, △ ABC 三个顶点的坐标分别为 A ( 1 , 1 ), B ( 4 , 2 ), C ( 3 , 4 ).
( 1 )在图中画出 △ ABC 关于 y 轴对称的图形 △ A 1 B 1 C 1 ,并写出点 A 1 的坐标;
( 2 )求 △ ABC 的面积;
( 3 )在 x 轴上有一点 P 使得 PA + PB 的值最小,则点 P 的坐标是 .
4、 观察下列一组式子的变形过程,然后回答问题:
例 1 :
例 2 : , ……
( 1 )填空: = ; = .
( 2 )利用上面的结论,求下列式子的值.
( 3 )根据你的推断,比较 和 的大小.
5、 暑假即将来临,某运动馆推出针对学生两种暑期优惠方案:
方案一:先办理 VIP 卡需 100 元,然后每次按全票价打五折;
方案二:学生每次按全票价打九折;
已知运动馆全票价为 20 元 / 次,回答下面问题:
( 1 )设方案一、方案二的费用分别为 y 1 、 y 2 ,直接写出 y 1 、 y 2 与去运动馆次数 x 的关系式;
( 2 )某同学估计暑假要去运动馆大概 10 次,请你帮他分析办 VIP 卡划算吗?
( 3 )去俱乐部健身至少 次办 VIP 卡才合算.
6、 阅读下面的材料,然后解答问题:
我们新定义一种三角形,两边的平方和等于第三边平方的 2 倍的三角形叫做奇异三角形.
( 1 )理解并填空:
① 根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗? (填 “ 是 ” 或 “ 不是 ” )
② 若某三角形的三边长分别为 1 、 、 2 ,则该三角形 (填 “ 是 ” 或 “ 不是 ” )奇异三角形.
( 2 )探究:在 中,两边长分别是 ,且 , ,则这个三角形是否是奇异三角形?请说明理由.
7、 如图,直线 : 与 轴, 轴分别交于 , 两点,点 为直线 上一点,另一直线 : 过点 .
( 1 )写出列各点的坐标 , ;
( 2 )求点 坐标和 的值;
( 3 )若点 在 轴上,且 是以 为腰的等腰三角形,则符合条件的 点有 个.
( 4 )若点 是直线 与 轴的交点,动点 从点 开始以每秒 1 个单位的速度向 轴正方向移动,设点 的运动时间为 秒;当 为何值时 的面积等于 4.5 ,并求出此时点 的坐标.
( 5 )若直线 : .与 , 可以围成三角形,直接写出 的取值范围 .
8、 某同学对函数 , , 的图象和性质进行探究:无论 为何值时,函数均有意义,所得自变量与函数的对应值如表.
x … ﹣ 3 ﹣ 2 ﹣ 1 0 1 2 3 …
y 1 … 1.5 1 0.5 0 0.5 1 1.5 …
y 2 … ﹣ 0.5 ﹣ 1 m ﹣ 2 ﹣ 1.5 ﹣ 1 ﹣ 0.5 …
y 3 … 2.5 n 1.5 1 1.5 2 2.5 …
( 1 )表中 m = , n = ;
( 2 )根据表中数据,补画函数图象位于 y 轴左边的部分.
( 3 )归纳函数 的性质:
① 函数 与 轴交点坐标是 ;
② 当 时, 随 的增大而增大;当 时, 随 的增大而减小.
( 4 )类比上述探究函数的图象与性质的过程,探究并写出函数 的性质;
① ;
② ; .
( 5 )对于函数 ,若函数值 ,请直接写出自变量 的取值范围: .
============参考答案============
一、选择题
1、 B
【分析】
无理数就是无限不循环小数,依据定义即可判断.
【详解】
在实数 , , 0 , , 0.070070007… (相令两个 7 之间 0 的个数逐次加 1 )中,无理数有 , , 0.070070007… (相令两个 7 之间 0 的个数逐次加 1 ),共 3 个,
故选 B .
【点睛】
此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如 .
2、 C
【分析】
根据确定位置的有序数对有两个数解答.
【详解】
解:在平面直角坐标系中,要用两个数据才能表示一个点的位置,
纵观各选项,只有东经 33° ,北纬 36° 能确定台风的位置.
故选 C .
【点睛】
本题考查坐标确定位置,理解在平面直角坐标系中,要用两个数据才能表示一个点的位置是解题关键.
3、 D
【分析】
根据函数的定义可知,满足对于 的每一个取值, 都有唯一确定的值与之对应关系,据此即可判断.
【详解】
解:由图象,得
D 的图象不满足对于 x 的每一个取值, y 都有唯一确定的值与之对应关系,
故选: D .
【点睛】
主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量 , ,对于 的每一个取值, 都有唯一确定的值与之对应,则 是 的函数, 叫自变量.
4、 C
【分析】
直接利用有关实数的性质分别分析得出答案.
【详解】
解: A 、实数分为正实数、负实数和 0 ,故选项错误,不符合题意;
B 、带根号的数不一定是无理数,例如 ,故选项错误,不符合题意;
C 、无限不循环小数都是无理数,故选项正确,符合题意;
D 、平方根等于本身的数是 0 ,故选项错误,不符合题意;
故选: C .
【点睛】
本题主要考查了实数,解题的关键是正确掌握实数的分类及概念.
5、 B
【分析】
根据相反数的概念及性质逐项分析解答即可.
【详解】
解: A 、 2 与 =2 ,不互为相反数,故选项错误;
B 、 -2 与 - =2 互为相反数,故选项正确;
C 、 与 2 不互为相反数,故选项错误;
D 、 |-3|=3 、 =3 , ,3 与 3 不互为相反数,故选项错误.
故选 B .
【点睛】
本题主要考查相反数的定义,掌握只有符号不同的两个数互为相反数是解答本题的关键.
6、 D
【分析】
利用勾股数定义勾股数就是可以构成一个直角三角形三边的一组正整数,勾股定理:直角三角形两条直角边 a 、 b 的平方和等于斜边 c 的平方( a + b = c )进行分析即可.
【详解】
解: A 、 9 2 +16 2 ≠25 2 ,不是勾股数,故选项 A 不是勾股数;
B 、 0.3 , 0.4 , 0.5 不是正整数,不是勾股数,故选项 B 不是勾股数;
C 、 不是正整数,不是勾股数,故选项 C 不是勾股数;
D 、 8 2 +15 2 =17 2 ,都是正整数,是勾股数,故此选项符合题意;
故选: D .
【点睛】
此题主要考查了勾股数,关键是掌握满足 a 2 + b 2 = c 2 的三个正整数,称为勾股数.
7、 C
【分析】
当地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,根据勾股定理求得 AB ,然后求得地毯的长度即可.
【详解】
解:由勾股定理得: AB = ,
因为地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
所以地毯的长度至少是 1.5+2=3.5 ( m ).
故选 C .
【点睛】
本题考查了图形平移性质和勾股定理,解决本题的关键是要熟练掌握勾股定理 .
8、 B
【分析】
由勾股定理得 E = A + B + C + D ,然后代入解方程即可得到结论.
【详解】
解 : 最大正方形的面积 E = 31 ,小正方形面积 A = 4 、 B = 9 、 C = 8 ,
根据勾股定理得: E = A + B + C + D ,
∴31=4+9+8+ D ,
∴ D =31-21=10 .
故选 B .
【点睛】
此题考查勾股定理,一元一次方程,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解题的关键.
9、 D
【分析】
点 P 到 x 轴的距离为点 P 的纵坐标的绝对值,点 P 到 y 轴的距离为点 P 的横坐标绝对值,再由点 P 所在的象限即可确定点 P 的坐标.
【详解】
由题意知,点 P 的坐标为 (5 , -4)
故选: D .
【点睛】
本题根据点到坐标轴的距离确定点的坐标,关键清楚点到坐标轴的距离与点的横纵坐标的绝对值有关.
10、 A
【分析】
“ 炮 ” 的坐标可以看作 “ 士 ” 向左移动 2 个单位,再向上移动 3 个单位得到.
【详解】
解: ∵“ 士 ” 的位置坐标为( 1 , 2 ),
∴ 由图形可知, “ 炮 ” 的横坐标是 “ 士 ” 向左移动 2 个单位即 1 2 = 3 ,纵坐标为 “ 士 ” 向上移动 3 个单位得到即 2 + 3 = 1 ,故 “ 炮 ” 的坐标是( 3 , 1 ).
故选: A .
【点睛】
本题考查了点的位置的确定,另一种解题思路为:可以通过已知 “ 士 ” , “ 相 ” 的坐标确定原点的位置,再确定 “ 炮 ” 的坐标.
11、 C
【分析】
求出 OA 、 OB ,根据勾股定理求出 AB ,即可得出 AC ,求出 OC 长即可.
【详解】
解: ∵ A ( 1 , 0 ), B ( 0 , 2 ),
∴ OA = 1 , OB = 2 ,
在 Rt △ AOB 中,由勾股定理得: AB = ,
∴ AC = AB = ,
∴ OC = ,
∴ 点 C 的横坐标为( ),
故选: C .
【点睛】
本题考查了勾股定理,实数的大小比较,坐标与图形性质的应用,解此题的关键是求出 OC 的长.
12、 A
【分析】
设正比例函数为 ,求出 ,再对选项逐个判断即可.
【详解】
解:设正比例函数为 ,
∵ 图象过点 (1 , -2)
∴ ,即
A : ,函数值随自变量的增大而减小,选项错误,符合题意;
B :选项正确,不符合题意;
C :当 时, ,经过点 (2 , -4) ,选项正确,不符合题意;
D : ,函数图象过二、四象限,选项正确,不符合题意;
故答案为 A .
【点睛】
此题主要考察了正比例函数的性质,熟练掌握正比例函数的性质是解题的关键.
13、 C
【分析】
首先结合数轴利用已知条件求出线段 CB 的长度,然后根据中点的性质即可求出点 A 表示的数.
【详解】
解: 数轴上表示 2 , 的对应点分别为 、 ,
,
点 是 的中点,
,
点 表示的数为 .
故选: C.
【点睛】
此题主要考查了实数与数轴,中点的性质,解题的关键是根据题意求出 AC 的长.
14、 B
【分析】
根据一次函数的性质,一次项系数大于 0 ,则函数图象一定经过第一,三象限,常数项 -7 < 0 ,则一定与 y 轴负半轴相交,据此即可判断.
【详解】
解: ∵ 一次函数 中, 1 > 0 , -7 < 0 ,
∴ 图象经过第一、三、四象限,即不经过第二象限.
故选: B .
【点睛】
本题考查了一次函数的图象.一次函数 y = kx + b 的图象有四种情况: ① 当 k > 0 , b > 0 ,函数 y = kx + b 的图象经过第一、二、三象限; ② 当 k > 0 , b < 0 ,函数 y = kx + b 的图象经过第一、三、四象限; ③ 当 k < 0 , b > 0 时,函数 y = kx + b 的图象经过第一、二、四象限; ④ 当 k < 0 , b < 0 时,函数 y = kx + b 的图象经过第二、三、四象限.
15、 D
【分析】
如图,画出圆柱的展开图,连接 AC ,由勾股定理即可求出 .
【详解】
如图所示,在 中, AB=10 cm , BC=10 cm ,
则 cm ,
∴ 装饰带的长度最短为 cm ,
故选 D.
【点睛】
本题考查勾股定理的展开图求最短距离问题,正确画出展开图是解题的关键 .
16、 C
【分析】
选项 A 根据函数图象的纵坐标即可得出答案;选项 B 根据函数图象的横坐标可得到达书店时间,离开书店时间,根据有理数的减法可得答案;选项 C 根据函数图象的纵坐标,可得相应的路程,根据有理数的加法可得答案;选项 D 根据函数图象的纵坐标可得路程,根据函数图象的横坐标可得时间,根据路程与时间的关系可得速度.
【详解】
解: A 、根据图象可得学校的纵坐标为 1500 ,小明家的纵坐标为 0 ,故小明家到学校的路程是 1500 米;故本选项不符合题意;
B 、根据题意,小明在书店停留的时间为从 8 分到 12 分,故小明在书店停留了 4 分钟;故本选项不符合题意;
C 、一共行驶的总路程 =1200+ ( 1200-600 ) + ( 1500-600 ) =2700 (米),故本选项符合题意;
D 、由图象可知: 0 到 6 分钟时,平均速度 = (米 / 分), 6 到 8 分钟时,平均速度 = (米 / 分), 12 到 14 分钟时,平均速度 = (米 / 分),所以 12 到 14 分钟时速度最快,不在安全限度内,故本选项不符合题意;
故选 C .
【点睛】
本题主要考查了函数图象,解题的关键是从函数图象得到基本信息进行求解.
17、 A
【分析】
根据一次函数与正比例函数的性质对四个选项进行逐一分析即可.
【详解】
解: A 、由一次函数的图象可知, m < 0 , n > 0 ,故 mn < 0 ;由正比例函数的图象可知 mn < 0 ,两结论一致,故本选项正确;
B 、由一次函数的图象可知, m < 0 , n > 0 ,故 mn < 0 ;由正比例函数的图象可知 mn > 0 ,两结论不一致,故本选项不正确;
C 、由一次函数的图象可知, m > 0 , n > 0 ,故 mn > 0 ;由正比例函数的图象可知 mn < 0 ,两结论不一致,故本选项不正确;
D 、由一次函数的图象可知, m > 0 , n < 0 ,故 mn < 0 ;由正比例函数的图象可知 mn > 0 ,两结论不一致,故本选项不正确.
故选: A .
【点睛】
此题主要考查了一次函数的图象性质,熟知一次函数的图象与系数的关系是解答此题的关键.
18、 D
【分析】
24 和 10 为两条直角边长时,求出小正方形的边长 14 ,即可利用勾股定理得出 EF 的长.
【详解】
解: ∵AE=10 , BE=24 ,即 24 和 10 为两条直角边长时,
小正方形的边长 =24-10=14 ,
∴EF= .
故选 D .
【点睛】
本题考查了勾股定理、正方形的性质;熟练掌握勾股定理是解决问题的关键.
19、 C
【分析】
用 2021 除以 12 即可知道物体运动了几周,且继续运动几个单位,由此可判断 2021 秒后物体的位置.
【详解】
解:由图可得,长方形的周长为 2× ( 1×2 + 2×2 )= 12 ,
∵2021 = 168×12 + 5 ,
∴ 经过 2021 秒后,该物体应运动了 168 圈,且继续运动 5 个单位,
∴ 从 A 点开始按逆时针运动 6 秒到达了 C 点左边一个单位长度,
∴ 经过 2021 秒后,物体所在位置的坐标为( 1 , 1 ).
故选: C .
【点睛】
本题主要考查平面直角坐标系、点的坐标规律,解决本题的关键是得出 2021 = 168×12 + 5 ,即经过 2021 秒后,该物体应运动了 168 圈,且继续运动 5 个单位.
20、 B
【分析】
连接 BF ,由折叠可知 AE 垂直平分 BF ,根据勾股定理求得 AE=5 ,利用直角三角形面积的两种表示法求得 BH= ,即可得 BF= ,再证明 ∠BFC=90° ,最后利用勾股定理求得 CF= .
【详解】
连接 BF ,由折叠可知 AE 垂直平分 BF ,
∵BC=6 ,点 E 为 BC 的中点,
∴BE=3 ,
又 ∵AB=4 ,
∴AE= =5 ,
∵ ,
∴ ,
∴BH= ,则 BF= ,
∵FE=BE=EC ,
∴∠BFC=90° ,
∴CF= = .
故选 B .
【点睛】
本题考查的是翻折变换的性质、矩形的性质及勾股定理的应用,掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.
21、 D
【分析】
由直线解析式:该直线过定点 ,画出图形,由图可知:在直线 和直线 之间,两侧格点相同,再根据 、 两点坐标求 的取值 .
【详解】
解: 直线 过定点 ,分布在直线 两侧的格点数相同,
由正方形的对称可知,直线 两侧的格点数相同,
在直线 和直线 之间,两侧格点相同,(如图)
, ,
,则 ,
故选: D .
【点睛】
此题考查的是一次函数与图形问题,根据一次函数的图象与点的坐标的位置关系求 的取值是解决此题的关键.
二、填空题
1、 y=2x+3
【分析】
根据 “ 上加下减 ” 的平移规律即可得出答案.
【详解】
解:把直线 y=2x 向上平移 3 个单位得到直线 y=2x+3 .
故答案为 y=2x+3 .
【点睛】
本题考查了一次函数图象与几何变换,直线平移变换的规律:对直线 y=kx 而言:上下移动,上加下减;左右移动,左加右减. ① 如上移 2 个单位,即 y=kx+2 ; ② 下移 2 个单位,即 y=kx ﹣ 2 . ③ 左移 2 个单位,即 y=k ( x+2 ); ④ 右移 2 个单位,即 y=k ( x ﹣ 2 ).掌握其中变与不变的规律是解决直线平移变换的好方法
2、
【分析】
先估算出 的范围,再减去 1 ,最后除以 4 即可.
【详解】
解: ,
,
,
即 ,
故答案为: .
【点睛】
本题考查了估算无理数的大小和实数的大小比较,解题的关键是能估算出 的范围.
3、
【分析】
依据正比例函数的定义求解即可.
【详解】
∵ 是关于 的正比例函数,
∴ , ,
解得: .
故答案为: .
【点睛】
本题主要考查的是正比例函数的定义,熟练掌握正比例函数的定义是解题的关键.
4、
【分析】
根据二次根式有意义的条件列出不等式,解不等式求出 ,代入原式求出 ,根据立方根的概念解答即可.
【详解】
解:由题意得, , ,
解得, ,
,
解得, ,
,
的立方根是 ,
故答案为: .
【点睛】
本题考查的是二次根式有意义的条件、立方根的概念,掌握二次根式的被开方数是非负数是解题的关键.
5、 (﹣ 4 , 2 )或( 6 , 2 )
【分析】
由直线 轴可确定点 B 的纵坐标为 2 ,然后分当点 B 在点 A 左边和点 B 在点 A 右边两种情况,结合 解答即可.
【详解】
解: ∵ AB ∥ x 轴,点 A 的坐标为( 1 , 2 ),
∴ 点 B 的纵坐标为 2 ,
∵ AB = 5 ,
∴ 点 B 在点 A 的左边时,横坐标为 1 ﹣ 5 =﹣ 4 ,
点 B 在点 A 的右边时,横坐标为 1+5 = 6 ,
∴ 点 B 的坐标为(﹣ 4 , 2 )或( 6 , 2 ).
故答案为(﹣ 4 , 2 )或( 6 , 2 ).
【点睛】
本题考查了图形与坐标,属于基础题目,正确分类、掌握解答的方法是解题关键.
6、
【分析】
根据一次函数的增减性判断即可;
【详解】
∵ ,
∴y 随 x 的增大而减小,
又 ∵ 点 A ( x 1 , y 1 )和 B ( x 2 , y 2 )都在直线 y =﹣ 3 x +2 上,且 x 1 < x 2 ,
∴ ,
故答案是: .
【点睛】
本题主要考查了一次函数图像的增减性,准确分析判断是解题的关键.
7、 14.5
【分析】
设 OA - OB = x 尺,表示出 OE 的长,在 Rt △ OEB 中,利用勾股定理列出关于 x 的方程,求出方程的解即可得到结果.
【详解】
解:设 OA = OB = x 尺,
∵ EC = BD =5 尺, AC =1 尺,
∴ EA = EC - AC =5-1=4 (尺),
OE = OA - AE = ( x -4 )尺,
在 Rt △ OEB 中, OE = ( x -4 )尺, OB = x 尺, EB =10 尺,
根据勾股定理得: x 2 = ( x -4 ) 2 +10 2 ,
整理得: 8 x =116 ,
即 2 x =29 ,
解得: x =14.5 ,
答:秋千绳索的长度是 14.5 尺.
故答案为: 14.5 .
【点睛】
此题考查了勾股定理的应用,熟练掌握勾股定理是解本题的关键.
8、
【分析】
先根据 , ,即可得到 , ,再根据 ,可得 ,进而得到 .
【详解】
解:由图可得, , , … , , , , ,
,
∴ ,即 ,
故答案为: .
【点睛】
本题主要考查了点的坐标变化规律,解决问题的关键是根据图形的变化规律得到 P 6 n ( 2 n , 0 ).
9、 “ 祝你成功 ”
【分析】
根据题意可以发现对应字之间的规律,从而可以解答本题.
【详解】
解:由题意可得,
“ 今天考试 ” 的真实意思是 “ 努力发挥 ” , “ 今 ” 所对应的字为 “ 努 ” ,是 “ 今 ” 字先向右平移一个单位,再向上平移两个单位得到的 “ 努 ” ,其他各个字对应也是这样得到的,
∴“ 正做数学 ” 后的真实意思是 “ 祝你成功 ” ,
故答案为: “ 祝你成功 ” .
【点睛】
本题考查坐标确定位置,解答本题的关键是发现对应字之间的规律.
三、解答题
1、 ( 1 ) 6 ;( 2 ) 0 ;( 3 ) ;( 4 ) 2 ;( 5 ) ;( 6 ) ,
【分析】
( 1 )利用二次根式的性质化简各数,再计算有理数的加减法即可求得答案;
( 2 )利用二次根式的性质化简各数,再合并同类二次根式即可求得答案;
( 3 )利用二次根式的性质、立方根的意义以及绝对值的意义化简各数,再合并同类二次根式即可求得答案;
( 4 )利用二次根式的乘除法法则计算,再计算有理数的加减法即可求得答案;
( 5 )利用完全平方公式以及平方差公式去括号,再合并同类二次根式即可求得答案;
( 6 )利用平方根的性质解方程即可.
【详解】
解:( 1 )原式
;
( 2 )原式
;
( 3 )原式
;
( 4 )原式
;
( 5 )原式
;
( 6 ) ∵ ( x ﹣ 1 ) 2 = 2 ,
∴ ,
∴ 或 ,
解得: , .
【点睛】
本题考查了二次根式的混合运算,熟练掌握二次根式的性质、运算法则以及平方根与立方根的意义是解决本题的关键.
2、 ( 1 )小亮;( 2 ) ;( 3 )
【分析】
( 1 )由 知 ,据此可得 ,从而做出判断;
( 2 )根据二次根式的性质 可得答案;
( 3 )利用二次根式的性质化简、代入求值即可得.
【详解】
解:( 1 ) ∵ , ∴ ,
则 ,
所以小亮的解法是错误的.
故答案为小亮;
( 2 )错误的原因在于未能正确的运用二次根式的性质 .
故答案为 .
( 3 )
∵
∴
∴
∴ 原式
【点睛】
本题考查了二次根式的化简求值,解题的关键是掌握二次根式的性质.
3、 ( 1 )作图见解析; ;( 2 ) ;( 3 )
【分析】
( 1 )根据关于 y 轴对称的特征求出 , , ,连接即可;
( 2 )根据补全法计算即可;
( 3 )过点 A 作 x 轴的对称点 ,连接 ,即可得到点 P 的位置,计算即可;
【详解】
( 1 ) ∵ A ( 1 , 1 ), B ( 4 , 2 ), C ( 3 , 4 ),
∴ 关于 y 轴对称的点是 , , ,
作图如下:
( 2 ) ;
( 3 )过点 A 作 x 轴的对称点 ,连接 ,如图所示,
即当 时,距离最小;
故答案是: .
【点睛】
本题主要考查了平面直角坐标系中点的对称和对称作图,准确分析计算是解题的关键.
4、 ( 1 ) , ;( 2 ) ;( 3 )
【分析】
( 1 )观察已知条件,利用分母有理化进行计算即可;
( 2 )根据规律可得 ,再计算即可;
( 3 )分别求得 和 的倒数,比较其倒数的大小,根据两个正数的倒数越小的数反而越大即可比较原数的大小.
【详解】
解:( 1 ) ,
,
故答案为: , ;
( 2 )原式 = ,
( 3 ) ,
,
,
即 ,
.
【点睛】
本题考查了分母有理化和平方差公式的运用,掌握分母有理化是解题的关键.
5、 ( 1 ) y 1 = 100+10 x , y 2 = 18 x ;( 2 )办 VIP 不划算,理由见解析;( 3 ) 13
【分析】
( 1 )先求出打折后单次的价格,再根据方案一、方案二,表示题中的数量关系,即可列出函数关系式;
( 2 )将 x = 10 代入( 1 )中的函数关系式,即可求出方案一及方案二的费用,继而判断是否需要办 VIP ;
( 3 )根据题意可得 100+10 x < 18 x ,进而解不等式即可求得答案.
【详解】
解:( 1 )根据题意可得: 20×50% = 10 (元 / 次), 20×90% = 18 (元 / 次),
∴ y 1 = 100+10 x , y 2 = 18 x ,
( 2 )办 VIP 不划算,理由如下:
当 x = 10 时,
方案一的费用为 y 1 = 100+10×10 = 200 ,
方案二的费用为 y 2 = 18×10 = 180 ,
∵200 > 180 ,
∴ y 1 > y 2 ,
∴ 办 VIP 不划算;
( 3 )由题意可得: y 1 < y 2 ,
∴100+10 x < 18 x ,
解得: x > 12.5 ,
∴ x 的最小整数解为 13 ,
∴ 去俱乐部健身至少 13 次办 VIP 卡才合算,
故答案为: 13 .
【点睛】
本题考查了一次函数与一元一次不等式的实际应用,体现了数学来源于生活又服务于生活,考查了学生的运算能力,应用能力等,本题关键在于能够用函数关系式表示量与量之间的关系,并进行比较,做出独立判断.
6、 ( 1 ) ① 是; ② 是;( 2 )当 为斜边时, 不是奇异三角形;当 为斜边时, 是奇异三角形.
【分析】
( 1 ) ① 根据等边三角形的三边相等、奇异三角形的定义判断;
② 根据奇异三角形的定义判断;
( 2 )分 c 为斜边、 b 为斜边两种情况,根据勾股定理、奇异三角形的定义判断.
【详解】
( 1 ) ① 设等边三角形的边长为 a ,则 ,
∴ 等边三角形一定是奇异三角形,
故答案为:是;
②∵ , 2× =8 ,
∴
∴ 该三角形是奇异三角形,
故答案为:是;
( 2 )当 c 为斜边时,则 ,
则
∴Rt△ABC 不是奇异三角形;
当 b 为斜边时, ,
则有 ,
∴Rt△ABC 是奇异三角形,
答:当 为斜边时, 不是奇异三角形;当 为斜边时, 是奇异三角形.
【点睛】
本题考查的是勾股定理、奇异三角形的定义,如果直角三角形的两条直角边长分别是 a , b ,斜边长为 c ,那么 .
7、 ( 1 ) , ;( 2 ) 的坐标为 , ;( 3 ) 3 ;( 4 ) 或 ;( 5 ) 且 或 且 .
【分析】
( 1 )分别令 , ,即可求得 , 两点的坐标;
( 2 )把 的坐标代入直线 上的解析式即可求得 的坐标,然后根据待定系数法即可求得 ;
( 3 )根据等腰三角形的性质,两腰相等,可以分别以 , 两点为圆心, 长为半径作弧分别与 轴交于两点,即为所求;
( 4 )根据直线 的解析式得出 的坐标,根据题意得出 ,然后根据 即可求得 的面积 与 的函数关系式;通过解方程 或 ,求得 的值,即可求得 的坐标;
( 5 )若直线 : .与 , 可以围成三角形,那么 不能与 , 平行,即可求得 的取值范围.
【详解】
解:( 1 ) ∵ 直线 : 与 轴, 轴分别交于 , 两点,
∴ 当 时, ,
则 ,
当 时, ,
∴ , ,
故答案为: , ;
( 2 ) 点 为直线 上一点,
,解得 ,
点 的坐标为 ,
把点 的坐标代入 得, ,
解得 ,
即点 的坐标为 , ;
( 3 )如图分别以 , 两点为圆心, 长为半径作弧与 轴交于 , , 3 个点.
故答案为: 3 ;
( 4 ) 直线 的解析式为 ,
点的坐标为 ,
由直线 可知 ,
当 在 、 之间时,
则 , ,
,
,
∴ ,
解得: ,
∴ ;
当 在 的右边时,
则 , ,
;
,
∴ ,
解得: ,
∴ ,
即 的坐标为 或 ;
( 5 )已知直线 : 过点 ,
情况一:如图当 时, ,
∴ 此时 与 , 不能围成三角形,
∴ 且 ; 与 , 可以围成三角形;
情况二:如图当 时, ,
∴ 此时 与 , 不能围成三角形,
∴ 且 ; 与 , 可以围成三角形;
故答案为: 且 或 且 .
【点睛】
本题是一次函数的综合题,考查了一次函数图象上的点的坐标特征,一次函数的性质,待定系数法求解析式以及三角形的面积等,分类讨论是解题关键.
8、 ( 1 ) , 2 ;( 2 )见解析;( 3 ) ① ; ② , ;( 4 ) ① 函数 与 轴交点坐标是 ; ② 当 时, 随 的增大而减小;当 时, 随 的增大而增大;( 5 ) .
【分析】
( 1 )当 时,根据 的解析式可得 ,当 时,根据 的解析式可得 ;
( 2 )根据表格数据描点连线绘制函数图象即可;
( 3 )根据函数图象归纳函数性质即可;
( 4 )类比上述探究函数的图象与性质的过程,画出函数 的图象,观察函数图象即可求解;
( 5 )画出函数 的图象,令 , ,解得: , ,从而可得函数值 时, 的取值范围.
【详解】
解:( 1 )当 时, ,
当 时, ,
故答案为: , 2 ;
( 2 )根据表格数据描点连线绘制函数图象如下所示:
( 3 )由图象得:归纳函数 的性质:
① 函数 与 轴交点坐标是 ;
② 当 时, 随 的增大而增大;当 时, 随 的增大而减小;
故答案为: ① ; ② , ;
( 4 )类比上述探究函数的图象与性质的过程,画出函数 , , 的图象,
由函数图象知函数 的图象的性质:
① 函数 与 轴交点坐标是 ;
② 当 时, 随 的增大而减小;当 时, 随 的增大而增大;
故答案为: ① 函数 与 轴交点坐标是 ;
② 当 时, 随 的增大而减小;当 时, 随 的增大而增大.
( 5 )令 , ,
解得: , ,
∴ 若函数值 ,
∴ 可得 ,
故答案为: .
【点睛】
本题考查了一次函数的图象与性质,一次函数图象上点的坐标特征.正确画出函数的图象,利用数形结合思想是解题的关键.
姓名:__________ 班级:__________考号:__________
一、选择题(共21题)
1、 在实数 , , 0 , , 0.070070007… (相令两个 7 之间 0 的个数逐次加 1 )中,无理数有( )
A . 2 个 B . 3 个 C . 4 个 D . 5 个
2、 气象台为了预报台风,首先要确定它的位置,下列说法中,能确定台风具体位置的是 ( )
A .西太平洋
B .距台湾 30 海里
C .东经 33° ,北纬 36°
D .台湾岛附近
3、 下列平面直角坐标系中的图象,不能表示 y 是 x 的函数的是( )
A . B .
C . D .
4、 下面说法中,正确的是( )
A .实数分为正实数和负实数 B .带根号的数都是无理数
C .无限不循环小数都是无理数 D .平方根等于本身的数是 1 和 0
5、 下列各组数中,互为相反数的一组是( ).
A . 2 与 B . 与 C . 与 D . 与
6、 各组数中,是勾股数的是( )
A . 9 , 16 , 25 B . 0.3 , 0.4 , 0.5 C . 1 , , 2 D . 8 , 15 , 17
7、 如图,是一段楼梯,高 BC 是 1.5m ,斜边 AC 是 2.5m ,如果在楼梯上铺地毯,那么至少需要地毯( )
A . 2.5m B . 3m C . 3.5m D . 4m
8、 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若最大正方形的面积 E = 31 ,小正方形面积 A = 4 、 B = 9 、 C = 8 则正方形 D 的面积是( )
A . 18 B . 10 C . 36 D . 40
9、 点 P 在四象限,且点 P 到 x 轴的距离为 4 ,点 P 到 y 轴的距离为 5 ,则点 P 的坐标为( )
A .(- 4 ,- 5 ) B .( 4 ,- 5 ) C .( 5 , 4 ) D .( 5 ,- 4 )
10、 如图,如果 “ 士 ” 的位置坐标为(﹣ 1 ,﹣ 2 ), “ 相 ” 的坐标为( 2 ,﹣ 2 ),则 “ 炮 ” 的坐标是( )
A .(﹣ 3 , 1 ) B .( 1 ,﹣ 1 ) C .(﹣ 2 , 1 ) D .(﹣ 3 , 3 )
11、 如图,在平面直角坐标系中, A (﹣ 1 , 0 ), B ( 0 , 2 ),以点 A 为圆心, AB 为半径画弧,交 x 轴正半轴于点 C ,点 C 的横坐标为( )
A . ﹣ 1 B . 2 C . ﹣ 1 D . 1 ﹣
12、 若正比例函数图象过点 (1 , -2) ,则下列说法不正确的是( )
A .函数值随自变量的增大而增大 B .函数值随自变量的增大而减小
C .函数图象过点 (2 , -4) D .函数图象过二、四象限
13、 如图,数轴上表示 2 、 的对应点分别记为 C 、 B ,点 C 是 的中点,则点 A 表示的数是( )
A . B . C . D .
14、 一次函数 的图象 不经过 的象限是( )
A .第一象限 B .第二象限 C .第三象限 D .第四象限
15、 今年 9 月 22 日是第三个中国农民丰收节,小彬用 3D 打印机制作了一个底面周长为 ,高为 的圆柱粮仓模型.如图 是底面直径, 是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过 , 两点(接头不计),则装饰带的长度最短为( )
A . B . C . D .
16、 小明从家骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与离家的距离的关系示意图,根据图中的信息回答下列问题,则下列说法错误的是( )
A .小明家到学校的路程是 米
B .小明在书店停留了 分钟
C .本次上学途中,小明一共行驶了 米
D .若骑单车的速度大于 米 / 分就有安全隐患.在整个上学的途中,小明骑车有 分钟的超速骑行,存在安全隐患.
17、 一次函数 y = mx + n 与正比例函数 y = mnx ( m , n 是常数,且 mn ≠0 ),在同一平面直角坐标系的图象是( )
A . B .
C . D .
18、 如图,是我国古代著名的 “ 赵爽弦图 ” 的示意图,此图是由四个全等的直角三角形拼接而成,其中 AE=10 , BE=24 ,则 EF 的长是( )
A . 14 B . 13 C . 14 D . 14
19、 如图,在平面直角坐标系中,长方形 ABCD 的各边分别平行于 x 轴或 y 轴,一物体从点 A (﹣ 2 , 1 )出发沿矩形 ABCD 的边按逆时针作环绕运动,速度为 1 个单位 / 秒,则经过 2021 秒后,物体所在位置的坐标为( )
A .( 2 , 0 ) B .(﹣ 2 ,﹣ 1 ) C .( 1 ,﹣ 1 ) D .( 2 , 1 )
20、 如图 , 在矩形 ABCD 中 ,AB=4,BC=6, 点 E 为 BC 的中点 , 将 ABE 沿 AE 折叠 , 使点 B 落在矩形内点 F 处 , 连接 CF, 则 CF 的长为( )
A . B . C . D .
21、 如图,在平面直角坐标系中有一个 3×3 的正方形网格,其右下角格点(小正方形的顶点) A 的坐标为(﹣ 1 , 1 ),左上角格点 B 的坐标为(﹣ 4 , 4 ),若分布在过定点(﹣ 1 , 0 )的直线 y =﹣ k ( x +1 )两侧的格点数相同,则 k 的取值可以是( )
A . B . 2 C . D .
二、填空题(共9题)
1、 把直线 y=2x 向上平移 3 个单位得到直线 _____ .
2、 比较大小: ______ .
3、 已知函数 ( 为常数),当 ____________ 时, 是 的正比例函数 .
4、 若 .则 的立方根是 ___ .
5、 已知点 A 的坐标为( 1 , 2 ),直线 AB ∥ x 轴,且 AB = 5 ,则点 B 坐标为 _______________ .
6、 点 A ( x 1 , y 1 )和 B ( x 2 , y 2 )都在直线 y =﹣ 3 x +2 上,且 x 1 < x 2 ,则 y 1 ___ y 2 .
7、 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》: “ 平地秋千未起,踏板一尺离地,送行二步恰竿齐,五尺板高离地 …” 翻译成现代文为:如图,秋千 OA 静止的时候,踏板离地高一尺( 尺),将它往前推进两步( 尺),此时踏板升高离地五尺( 尺),则秋千绳索( OA 或 OB )的长度为 ______ 尺.
8、 如图,在平面直角坐标系中,一动点沿箭头所示的方向,每次移动一个单位长度,依次得到点 , , , , , … ,则 的坐标是 ________ .
9、 “ 一把钥匙一把锁 ” ,请运用数学思维破译 “ 密码 ” ,小王同学目前已破译出 “ 今天考试 ” 的真实意思是 “ 努力发挥 ” ,那么破译 “ 正做数学 ” 的真实意思是 ________________ .
三、解答题(共8题)
1、 计算:
( 1 )
( 2 )
( 3 )
( 4 )
( 5 ) .
( 6 )求满足 x 的值:( x ﹣ 1 ) 2 = 2 .
2、 求代数式 a + 的值,其中 a = 1007 ,如图是小亮和小芳的解答过程.
( 1 ) 的解法是错误的;
( 2 )错误的原因在于未能正确的运用二次根式的性质: ;
( 3 )求代数式 a +2 的值,其中 a =﹣ 2022 .
3、 如图, △ ABC 三个顶点的坐标分别为 A ( 1 , 1 ), B ( 4 , 2 ), C ( 3 , 4 ).
( 1 )在图中画出 △ ABC 关于 y 轴对称的图形 △ A 1 B 1 C 1 ,并写出点 A 1 的坐标;
( 2 )求 △ ABC 的面积;
( 3 )在 x 轴上有一点 P 使得 PA + PB 的值最小,则点 P 的坐标是 .
4、 观察下列一组式子的变形过程,然后回答问题:
例 1 :
例 2 : , ……
( 1 )填空: = ; = .
( 2 )利用上面的结论,求下列式子的值.
( 3 )根据你的推断,比较 和 的大小.
5、 暑假即将来临,某运动馆推出针对学生两种暑期优惠方案:
方案一:先办理 VIP 卡需 100 元,然后每次按全票价打五折;
方案二:学生每次按全票价打九折;
已知运动馆全票价为 20 元 / 次,回答下面问题:
( 1 )设方案一、方案二的费用分别为 y 1 、 y 2 ,直接写出 y 1 、 y 2 与去运动馆次数 x 的关系式;
( 2 )某同学估计暑假要去运动馆大概 10 次,请你帮他分析办 VIP 卡划算吗?
( 3 )去俱乐部健身至少 次办 VIP 卡才合算.
6、 阅读下面的材料,然后解答问题:
我们新定义一种三角形,两边的平方和等于第三边平方的 2 倍的三角形叫做奇异三角形.
( 1 )理解并填空:
① 根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗? (填 “ 是 ” 或 “ 不是 ” )
② 若某三角形的三边长分别为 1 、 、 2 ,则该三角形 (填 “ 是 ” 或 “ 不是 ” )奇异三角形.
( 2 )探究:在 中,两边长分别是 ,且 , ,则这个三角形是否是奇异三角形?请说明理由.
7、 如图,直线 : 与 轴, 轴分别交于 , 两点,点 为直线 上一点,另一直线 : 过点 .
( 1 )写出列各点的坐标 , ;
( 2 )求点 坐标和 的值;
( 3 )若点 在 轴上,且 是以 为腰的等腰三角形,则符合条件的 点有 个.
( 4 )若点 是直线 与 轴的交点,动点 从点 开始以每秒 1 个单位的速度向 轴正方向移动,设点 的运动时间为 秒;当 为何值时 的面积等于 4.5 ,并求出此时点 的坐标.
( 5 )若直线 : .与 , 可以围成三角形,直接写出 的取值范围 .
8、 某同学对函数 , , 的图象和性质进行探究:无论 为何值时,函数均有意义,所得自变量与函数的对应值如表.
x … ﹣ 3 ﹣ 2 ﹣ 1 0 1 2 3 …
y 1 … 1.5 1 0.5 0 0.5 1 1.5 …
y 2 … ﹣ 0.5 ﹣ 1 m ﹣ 2 ﹣ 1.5 ﹣ 1 ﹣ 0.5 …
y 3 … 2.5 n 1.5 1 1.5 2 2.5 …
( 1 )表中 m = , n = ;
( 2 )根据表中数据,补画函数图象位于 y 轴左边的部分.
( 3 )归纳函数 的性质:
① 函数 与 轴交点坐标是 ;
② 当 时, 随 的增大而增大;当 时, 随 的增大而减小.
( 4 )类比上述探究函数的图象与性质的过程,探究并写出函数 的性质;
① ;
② ; .
( 5 )对于函数 ,若函数值 ,请直接写出自变量 的取值范围: .
============参考答案============
一、选择题
1、 B
【分析】
无理数就是无限不循环小数,依据定义即可判断.
【详解】
在实数 , , 0 , , 0.070070007… (相令两个 7 之间 0 的个数逐次加 1 )中,无理数有 , , 0.070070007… (相令两个 7 之间 0 的个数逐次加 1 ),共 3 个,
故选 B .
【点睛】
此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如 .
2、 C
【分析】
根据确定位置的有序数对有两个数解答.
【详解】
解:在平面直角坐标系中,要用两个数据才能表示一个点的位置,
纵观各选项,只有东经 33° ,北纬 36° 能确定台风的位置.
故选 C .
【点睛】
本题考查坐标确定位置,理解在平面直角坐标系中,要用两个数据才能表示一个点的位置是解题关键.
3、 D
【分析】
根据函数的定义可知,满足对于 的每一个取值, 都有唯一确定的值与之对应关系,据此即可判断.
【详解】
解:由图象,得
D 的图象不满足对于 x 的每一个取值, y 都有唯一确定的值与之对应关系,
故选: D .
【点睛】
主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量 , ,对于 的每一个取值, 都有唯一确定的值与之对应,则 是 的函数, 叫自变量.
4、 C
【分析】
直接利用有关实数的性质分别分析得出答案.
【详解】
解: A 、实数分为正实数、负实数和 0 ,故选项错误,不符合题意;
B 、带根号的数不一定是无理数,例如 ,故选项错误,不符合题意;
C 、无限不循环小数都是无理数,故选项正确,符合题意;
D 、平方根等于本身的数是 0 ,故选项错误,不符合题意;
故选: C .
【点睛】
本题主要考查了实数,解题的关键是正确掌握实数的分类及概念.
5、 B
【分析】
根据相反数的概念及性质逐项分析解答即可.
【详解】
解: A 、 2 与 =2 ,不互为相反数,故选项错误;
B 、 -2 与 - =2 互为相反数,故选项正确;
C 、 与 2 不互为相反数,故选项错误;
D 、 |-3|=3 、 =3 , ,3 与 3 不互为相反数,故选项错误.
故选 B .
【点睛】
本题主要考查相反数的定义,掌握只有符号不同的两个数互为相反数是解答本题的关键.
6、 D
【分析】
利用勾股数定义勾股数就是可以构成一个直角三角形三边的一组正整数,勾股定理:直角三角形两条直角边 a 、 b 的平方和等于斜边 c 的平方( a + b = c )进行分析即可.
【详解】
解: A 、 9 2 +16 2 ≠25 2 ,不是勾股数,故选项 A 不是勾股数;
B 、 0.3 , 0.4 , 0.5 不是正整数,不是勾股数,故选项 B 不是勾股数;
C 、 不是正整数,不是勾股数,故选项 C 不是勾股数;
D 、 8 2 +15 2 =17 2 ,都是正整数,是勾股数,故此选项符合题意;
故选: D .
【点睛】
此题主要考查了勾股数,关键是掌握满足 a 2 + b 2 = c 2 的三个正整数,称为勾股数.
7、 C
【分析】
当地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,根据勾股定理求得 AB ,然后求得地毯的长度即可.
【详解】
解:由勾股定理得: AB = ,
因为地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和,
所以地毯的长度至少是 1.5+2=3.5 ( m ).
故选 C .
【点睛】
本题考查了图形平移性质和勾股定理,解决本题的关键是要熟练掌握勾股定理 .
8、 B
【分析】
由勾股定理得 E = A + B + C + D ,然后代入解方程即可得到结论.
【详解】
解 : 最大正方形的面积 E = 31 ,小正方形面积 A = 4 、 B = 9 、 C = 8 ,
根据勾股定理得: E = A + B + C + D ,
∴31=4+9+8+ D ,
∴ D =31-21=10 .
故选 B .
【点睛】
此题考查勾股定理,一元一次方程,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解题的关键.
9、 D
【分析】
点 P 到 x 轴的距离为点 P 的纵坐标的绝对值,点 P 到 y 轴的距离为点 P 的横坐标绝对值,再由点 P 所在的象限即可确定点 P 的坐标.
【详解】
由题意知,点 P 的坐标为 (5 , -4)
故选: D .
【点睛】
本题根据点到坐标轴的距离确定点的坐标,关键清楚点到坐标轴的距离与点的横纵坐标的绝对值有关.
10、 A
【分析】
“ 炮 ” 的坐标可以看作 “ 士 ” 向左移动 2 个单位,再向上移动 3 个单位得到.
【详解】
解: ∵“ 士 ” 的位置坐标为( 1 , 2 ),
∴ 由图形可知, “ 炮 ” 的横坐标是 “ 士 ” 向左移动 2 个单位即 1 2 = 3 ,纵坐标为 “ 士 ” 向上移动 3 个单位得到即 2 + 3 = 1 ,故 “ 炮 ” 的坐标是( 3 , 1 ).
故选: A .
【点睛】
本题考查了点的位置的确定,另一种解题思路为:可以通过已知 “ 士 ” , “ 相 ” 的坐标确定原点的位置,再确定 “ 炮 ” 的坐标.
11、 C
【分析】
求出 OA 、 OB ,根据勾股定理求出 AB ,即可得出 AC ,求出 OC 长即可.
【详解】
解: ∵ A ( 1 , 0 ), B ( 0 , 2 ),
∴ OA = 1 , OB = 2 ,
在 Rt △ AOB 中,由勾股定理得: AB = ,
∴ AC = AB = ,
∴ OC = ,
∴ 点 C 的横坐标为( ),
故选: C .
【点睛】
本题考查了勾股定理,实数的大小比较,坐标与图形性质的应用,解此题的关键是求出 OC 的长.
12、 A
【分析】
设正比例函数为 ,求出 ,再对选项逐个判断即可.
【详解】
解:设正比例函数为 ,
∵ 图象过点 (1 , -2)
∴ ,即
A : ,函数值随自变量的增大而减小,选项错误,符合题意;
B :选项正确,不符合题意;
C :当 时, ,经过点 (2 , -4) ,选项正确,不符合题意;
D : ,函数图象过二、四象限,选项正确,不符合题意;
故答案为 A .
【点睛】
此题主要考察了正比例函数的性质,熟练掌握正比例函数的性质是解题的关键.
13、 C
【分析】
首先结合数轴利用已知条件求出线段 CB 的长度,然后根据中点的性质即可求出点 A 表示的数.
【详解】
解: 数轴上表示 2 , 的对应点分别为 、 ,
,
点 是 的中点,
,
点 表示的数为 .
故选: C.
【点睛】
此题主要考查了实数与数轴,中点的性质,解题的关键是根据题意求出 AC 的长.
14、 B
【分析】
根据一次函数的性质,一次项系数大于 0 ,则函数图象一定经过第一,三象限,常数项 -7 < 0 ,则一定与 y 轴负半轴相交,据此即可判断.
【详解】
解: ∵ 一次函数 中, 1 > 0 , -7 < 0 ,
∴ 图象经过第一、三、四象限,即不经过第二象限.
故选: B .
【点睛】
本题考查了一次函数的图象.一次函数 y = kx + b 的图象有四种情况: ① 当 k > 0 , b > 0 ,函数 y = kx + b 的图象经过第一、二、三象限; ② 当 k > 0 , b < 0 ,函数 y = kx + b 的图象经过第一、三、四象限; ③ 当 k < 0 , b > 0 时,函数 y = kx + b 的图象经过第一、二、四象限; ④ 当 k < 0 , b < 0 时,函数 y = kx + b 的图象经过第二、三、四象限.
15、 D
【分析】
如图,画出圆柱的展开图,连接 AC ,由勾股定理即可求出 .
【详解】
如图所示,在 中, AB=10 cm , BC=10 cm ,
则 cm ,
∴ 装饰带的长度最短为 cm ,
故选 D.
【点睛】
本题考查勾股定理的展开图求最短距离问题,正确画出展开图是解题的关键 .
16、 C
【分析】
选项 A 根据函数图象的纵坐标即可得出答案;选项 B 根据函数图象的横坐标可得到达书店时间,离开书店时间,根据有理数的减法可得答案;选项 C 根据函数图象的纵坐标,可得相应的路程,根据有理数的加法可得答案;选项 D 根据函数图象的纵坐标可得路程,根据函数图象的横坐标可得时间,根据路程与时间的关系可得速度.
【详解】
解: A 、根据图象可得学校的纵坐标为 1500 ,小明家的纵坐标为 0 ,故小明家到学校的路程是 1500 米;故本选项不符合题意;
B 、根据题意,小明在书店停留的时间为从 8 分到 12 分,故小明在书店停留了 4 分钟;故本选项不符合题意;
C 、一共行驶的总路程 =1200+ ( 1200-600 ) + ( 1500-600 ) =2700 (米),故本选项符合题意;
D 、由图象可知: 0 到 6 分钟时,平均速度 = (米 / 分), 6 到 8 分钟时,平均速度 = (米 / 分), 12 到 14 分钟时,平均速度 = (米 / 分),所以 12 到 14 分钟时速度最快,不在安全限度内,故本选项不符合题意;
故选 C .
【点睛】
本题主要考查了函数图象,解题的关键是从函数图象得到基本信息进行求解.
17、 A
【分析】
根据一次函数与正比例函数的性质对四个选项进行逐一分析即可.
【详解】
解: A 、由一次函数的图象可知, m < 0 , n > 0 ,故 mn < 0 ;由正比例函数的图象可知 mn < 0 ,两结论一致,故本选项正确;
B 、由一次函数的图象可知, m < 0 , n > 0 ,故 mn < 0 ;由正比例函数的图象可知 mn > 0 ,两结论不一致,故本选项不正确;
C 、由一次函数的图象可知, m > 0 , n > 0 ,故 mn > 0 ;由正比例函数的图象可知 mn < 0 ,两结论不一致,故本选项不正确;
D 、由一次函数的图象可知, m > 0 , n < 0 ,故 mn < 0 ;由正比例函数的图象可知 mn > 0 ,两结论不一致,故本选项不正确.
故选: A .
【点睛】
此题主要考查了一次函数的图象性质,熟知一次函数的图象与系数的关系是解答此题的关键.
18、 D
【分析】
24 和 10 为两条直角边长时,求出小正方形的边长 14 ,即可利用勾股定理得出 EF 的长.
【详解】
解: ∵AE=10 , BE=24 ,即 24 和 10 为两条直角边长时,
小正方形的边长 =24-10=14 ,
∴EF= .
故选 D .
【点睛】
本题考查了勾股定理、正方形的性质;熟练掌握勾股定理是解决问题的关键.
19、 C
【分析】
用 2021 除以 12 即可知道物体运动了几周,且继续运动几个单位,由此可判断 2021 秒后物体的位置.
【详解】
解:由图可得,长方形的周长为 2× ( 1×2 + 2×2 )= 12 ,
∵2021 = 168×12 + 5 ,
∴ 经过 2021 秒后,该物体应运动了 168 圈,且继续运动 5 个单位,
∴ 从 A 点开始按逆时针运动 6 秒到达了 C 点左边一个单位长度,
∴ 经过 2021 秒后,物体所在位置的坐标为( 1 , 1 ).
故选: C .
【点睛】
本题主要考查平面直角坐标系、点的坐标规律,解决本题的关键是得出 2021 = 168×12 + 5 ,即经过 2021 秒后,该物体应运动了 168 圈,且继续运动 5 个单位.
20、 B
【分析】
连接 BF ,由折叠可知 AE 垂直平分 BF ,根据勾股定理求得 AE=5 ,利用直角三角形面积的两种表示法求得 BH= ,即可得 BF= ,再证明 ∠BFC=90° ,最后利用勾股定理求得 CF= .
【详解】
连接 BF ,由折叠可知 AE 垂直平分 BF ,
∵BC=6 ,点 E 为 BC 的中点,
∴BE=3 ,
又 ∵AB=4 ,
∴AE= =5 ,
∵ ,
∴ ,
∴BH= ,则 BF= ,
∵FE=BE=EC ,
∴∠BFC=90° ,
∴CF= = .
故选 B .
【点睛】
本题考查的是翻折变换的性质、矩形的性质及勾股定理的应用,掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.
21、 D
【分析】
由直线解析式:该直线过定点 ,画出图形,由图可知:在直线 和直线 之间,两侧格点相同,再根据 、 两点坐标求 的取值 .
【详解】
解: 直线 过定点 ,分布在直线 两侧的格点数相同,
由正方形的对称可知,直线 两侧的格点数相同,
在直线 和直线 之间,两侧格点相同,(如图)
, ,
,则 ,
故选: D .
【点睛】
此题考查的是一次函数与图形问题,根据一次函数的图象与点的坐标的位置关系求 的取值是解决此题的关键.
二、填空题
1、 y=2x+3
【分析】
根据 “ 上加下减 ” 的平移规律即可得出答案.
【详解】
解:把直线 y=2x 向上平移 3 个单位得到直线 y=2x+3 .
故答案为 y=2x+3 .
【点睛】
本题考查了一次函数图象与几何变换,直线平移变换的规律:对直线 y=kx 而言:上下移动,上加下减;左右移动,左加右减. ① 如上移 2 个单位,即 y=kx+2 ; ② 下移 2 个单位,即 y=kx ﹣ 2 . ③ 左移 2 个单位,即 y=k ( x+2 ); ④ 右移 2 个单位,即 y=k ( x ﹣ 2 ).掌握其中变与不变的规律是解决直线平移变换的好方法
2、
【分析】
先估算出 的范围,再减去 1 ,最后除以 4 即可.
【详解】
解: ,
,
,
即 ,
故答案为: .
【点睛】
本题考查了估算无理数的大小和实数的大小比较,解题的关键是能估算出 的范围.
3、
【分析】
依据正比例函数的定义求解即可.
【详解】
∵ 是关于 的正比例函数,
∴ , ,
解得: .
故答案为: .
【点睛】
本题主要考查的是正比例函数的定义,熟练掌握正比例函数的定义是解题的关键.
4、
【分析】
根据二次根式有意义的条件列出不等式,解不等式求出 ,代入原式求出 ,根据立方根的概念解答即可.
【详解】
解:由题意得, , ,
解得, ,
,
解得, ,
,
的立方根是 ,
故答案为: .
【点睛】
本题考查的是二次根式有意义的条件、立方根的概念,掌握二次根式的被开方数是非负数是解题的关键.
5、 (﹣ 4 , 2 )或( 6 , 2 )
【分析】
由直线 轴可确定点 B 的纵坐标为 2 ,然后分当点 B 在点 A 左边和点 B 在点 A 右边两种情况,结合 解答即可.
【详解】
解: ∵ AB ∥ x 轴,点 A 的坐标为( 1 , 2 ),
∴ 点 B 的纵坐标为 2 ,
∵ AB = 5 ,
∴ 点 B 在点 A 的左边时,横坐标为 1 ﹣ 5 =﹣ 4 ,
点 B 在点 A 的右边时,横坐标为 1+5 = 6 ,
∴ 点 B 的坐标为(﹣ 4 , 2 )或( 6 , 2 ).
故答案为(﹣ 4 , 2 )或( 6 , 2 ).
【点睛】
本题考查了图形与坐标,属于基础题目,正确分类、掌握解答的方法是解题关键.
6、
【分析】
根据一次函数的增减性判断即可;
【详解】
∵ ,
∴y 随 x 的增大而减小,
又 ∵ 点 A ( x 1 , y 1 )和 B ( x 2 , y 2 )都在直线 y =﹣ 3 x +2 上,且 x 1 < x 2 ,
∴ ,
故答案是: .
【点睛】
本题主要考查了一次函数图像的增减性,准确分析判断是解题的关键.
7、 14.5
【分析】
设 OA - OB = x 尺,表示出 OE 的长,在 Rt △ OEB 中,利用勾股定理列出关于 x 的方程,求出方程的解即可得到结果.
【详解】
解:设 OA = OB = x 尺,
∵ EC = BD =5 尺, AC =1 尺,
∴ EA = EC - AC =5-1=4 (尺),
OE = OA - AE = ( x -4 )尺,
在 Rt △ OEB 中, OE = ( x -4 )尺, OB = x 尺, EB =10 尺,
根据勾股定理得: x 2 = ( x -4 ) 2 +10 2 ,
整理得: 8 x =116 ,
即 2 x =29 ,
解得: x =14.5 ,
答:秋千绳索的长度是 14.5 尺.
故答案为: 14.5 .
【点睛】
此题考查了勾股定理的应用,熟练掌握勾股定理是解本题的关键.
8、
【分析】
先根据 , ,即可得到 , ,再根据 ,可得 ,进而得到 .
【详解】
解:由图可得, , , … , , , , ,
,
∴ ,即 ,
故答案为: .
【点睛】
本题主要考查了点的坐标变化规律,解决问题的关键是根据图形的变化规律得到 P 6 n ( 2 n , 0 ).
9、 “ 祝你成功 ”
【分析】
根据题意可以发现对应字之间的规律,从而可以解答本题.
【详解】
解:由题意可得,
“ 今天考试 ” 的真实意思是 “ 努力发挥 ” , “ 今 ” 所对应的字为 “ 努 ” ,是 “ 今 ” 字先向右平移一个单位,再向上平移两个单位得到的 “ 努 ” ,其他各个字对应也是这样得到的,
∴“ 正做数学 ” 后的真实意思是 “ 祝你成功 ” ,
故答案为: “ 祝你成功 ” .
【点睛】
本题考查坐标确定位置,解答本题的关键是发现对应字之间的规律.
三、解答题
1、 ( 1 ) 6 ;( 2 ) 0 ;( 3 ) ;( 4 ) 2 ;( 5 ) ;( 6 ) ,
【分析】
( 1 )利用二次根式的性质化简各数,再计算有理数的加减法即可求得答案;
( 2 )利用二次根式的性质化简各数,再合并同类二次根式即可求得答案;
( 3 )利用二次根式的性质、立方根的意义以及绝对值的意义化简各数,再合并同类二次根式即可求得答案;
( 4 )利用二次根式的乘除法法则计算,再计算有理数的加减法即可求得答案;
( 5 )利用完全平方公式以及平方差公式去括号,再合并同类二次根式即可求得答案;
( 6 )利用平方根的性质解方程即可.
【详解】
解:( 1 )原式
;
( 2 )原式
;
( 3 )原式
;
( 4 )原式
;
( 5 )原式
;
( 6 ) ∵ ( x ﹣ 1 ) 2 = 2 ,
∴ ,
∴ 或 ,
解得: , .
【点睛】
本题考查了二次根式的混合运算,熟练掌握二次根式的性质、运算法则以及平方根与立方根的意义是解决本题的关键.
2、 ( 1 )小亮;( 2 ) ;( 3 )
【分析】
( 1 )由 知 ,据此可得 ,从而做出判断;
( 2 )根据二次根式的性质 可得答案;
( 3 )利用二次根式的性质化简、代入求值即可得.
【详解】
解:( 1 ) ∵ , ∴ ,
则 ,
所以小亮的解法是错误的.
故答案为小亮;
( 2 )错误的原因在于未能正确的运用二次根式的性质 .
故答案为 .
( 3 )
∵
∴
∴
∴ 原式
【点睛】
本题考查了二次根式的化简求值,解题的关键是掌握二次根式的性质.
3、 ( 1 )作图见解析; ;( 2 ) ;( 3 )
【分析】
( 1 )根据关于 y 轴对称的特征求出 , , ,连接即可;
( 2 )根据补全法计算即可;
( 3 )过点 A 作 x 轴的对称点 ,连接 ,即可得到点 P 的位置,计算即可;
【详解】
( 1 ) ∵ A ( 1 , 1 ), B ( 4 , 2 ), C ( 3 , 4 ),
∴ 关于 y 轴对称的点是 , , ,
作图如下:
( 2 ) ;
( 3 )过点 A 作 x 轴的对称点 ,连接 ,如图所示,
即当 时,距离最小;
故答案是: .
【点睛】
本题主要考查了平面直角坐标系中点的对称和对称作图,准确分析计算是解题的关键.
4、 ( 1 ) , ;( 2 ) ;( 3 )
【分析】
( 1 )观察已知条件,利用分母有理化进行计算即可;
( 2 )根据规律可得 ,再计算即可;
( 3 )分别求得 和 的倒数,比较其倒数的大小,根据两个正数的倒数越小的数反而越大即可比较原数的大小.
【详解】
解:( 1 ) ,
,
故答案为: , ;
( 2 )原式 = ,
( 3 ) ,
,
,
即 ,
.
【点睛】
本题考查了分母有理化和平方差公式的运用,掌握分母有理化是解题的关键.
5、 ( 1 ) y 1 = 100+10 x , y 2 = 18 x ;( 2 )办 VIP 不划算,理由见解析;( 3 ) 13
【分析】
( 1 )先求出打折后单次的价格,再根据方案一、方案二,表示题中的数量关系,即可列出函数关系式;
( 2 )将 x = 10 代入( 1 )中的函数关系式,即可求出方案一及方案二的费用,继而判断是否需要办 VIP ;
( 3 )根据题意可得 100+10 x < 18 x ,进而解不等式即可求得答案.
【详解】
解:( 1 )根据题意可得: 20×50% = 10 (元 / 次), 20×90% = 18 (元 / 次),
∴ y 1 = 100+10 x , y 2 = 18 x ,
( 2 )办 VIP 不划算,理由如下:
当 x = 10 时,
方案一的费用为 y 1 = 100+10×10 = 200 ,
方案二的费用为 y 2 = 18×10 = 180 ,
∵200 > 180 ,
∴ y 1 > y 2 ,
∴ 办 VIP 不划算;
( 3 )由题意可得: y 1 < y 2 ,
∴100+10 x < 18 x ,
解得: x > 12.5 ,
∴ x 的最小整数解为 13 ,
∴ 去俱乐部健身至少 13 次办 VIP 卡才合算,
故答案为: 13 .
【点睛】
本题考查了一次函数与一元一次不等式的实际应用,体现了数学来源于生活又服务于生活,考查了学生的运算能力,应用能力等,本题关键在于能够用函数关系式表示量与量之间的关系,并进行比较,做出独立判断.
6、 ( 1 ) ① 是; ② 是;( 2 )当 为斜边时, 不是奇异三角形;当 为斜边时, 是奇异三角形.
【分析】
( 1 ) ① 根据等边三角形的三边相等、奇异三角形的定义判断;
② 根据奇异三角形的定义判断;
( 2 )分 c 为斜边、 b 为斜边两种情况,根据勾股定理、奇异三角形的定义判断.
【详解】
( 1 ) ① 设等边三角形的边长为 a ,则 ,
∴ 等边三角形一定是奇异三角形,
故答案为:是;
②∵ , 2× =8 ,
∴
∴ 该三角形是奇异三角形,
故答案为:是;
( 2 )当 c 为斜边时,则 ,
则
∴Rt△ABC 不是奇异三角形;
当 b 为斜边时, ,
则有 ,
∴Rt△ABC 是奇异三角形,
答:当 为斜边时, 不是奇异三角形;当 为斜边时, 是奇异三角形.
【点睛】
本题考查的是勾股定理、奇异三角形的定义,如果直角三角形的两条直角边长分别是 a , b ,斜边长为 c ,那么 .
7、 ( 1 ) , ;( 2 ) 的坐标为 , ;( 3 ) 3 ;( 4 ) 或 ;( 5 ) 且 或 且 .
【分析】
( 1 )分别令 , ,即可求得 , 两点的坐标;
( 2 )把 的坐标代入直线 上的解析式即可求得 的坐标,然后根据待定系数法即可求得 ;
( 3 )根据等腰三角形的性质,两腰相等,可以分别以 , 两点为圆心, 长为半径作弧分别与 轴交于两点,即为所求;
( 4 )根据直线 的解析式得出 的坐标,根据题意得出 ,然后根据 即可求得 的面积 与 的函数关系式;通过解方程 或 ,求得 的值,即可求得 的坐标;
( 5 )若直线 : .与 , 可以围成三角形,那么 不能与 , 平行,即可求得 的取值范围.
【详解】
解:( 1 ) ∵ 直线 : 与 轴, 轴分别交于 , 两点,
∴ 当 时, ,
则 ,
当 时, ,
∴ , ,
故答案为: , ;
( 2 ) 点 为直线 上一点,
,解得 ,
点 的坐标为 ,
把点 的坐标代入 得, ,
解得 ,
即点 的坐标为 , ;
( 3 )如图分别以 , 两点为圆心, 长为半径作弧与 轴交于 , , 3 个点.
故答案为: 3 ;
( 4 ) 直线 的解析式为 ,
点的坐标为 ,
由直线 可知 ,
当 在 、 之间时,
则 , ,
,
,
∴ ,
解得: ,
∴ ;
当 在 的右边时,
则 , ,
;
,
∴ ,
解得: ,
∴ ,
即 的坐标为 或 ;
( 5 )已知直线 : 过点 ,
情况一:如图当 时, ,
∴ 此时 与 , 不能围成三角形,
∴ 且 ; 与 , 可以围成三角形;
情况二:如图当 时, ,
∴ 此时 与 , 不能围成三角形,
∴ 且 ; 与 , 可以围成三角形;
故答案为: 且 或 且 .
【点睛】
本题是一次函数的综合题,考查了一次函数图象上的点的坐标特征,一次函数的性质,待定系数法求解析式以及三角形的面积等,分类讨论是解题关键.
8、 ( 1 ) , 2 ;( 2 )见解析;( 3 ) ① ; ② , ;( 4 ) ① 函数 与 轴交点坐标是 ; ② 当 时, 随 的增大而减小;当 时, 随 的增大而增大;( 5 ) .
【分析】
( 1 )当 时,根据 的解析式可得 ,当 时,根据 的解析式可得 ;
( 2 )根据表格数据描点连线绘制函数图象即可;
( 3 )根据函数图象归纳函数性质即可;
( 4 )类比上述探究函数的图象与性质的过程,画出函数 的图象,观察函数图象即可求解;
( 5 )画出函数 的图象,令 , ,解得: , ,从而可得函数值 时, 的取值范围.
【详解】
解:( 1 )当 时, ,
当 时, ,
故答案为: , 2 ;
( 2 )根据表格数据描点连线绘制函数图象如下所示:
( 3 )由图象得:归纳函数 的性质:
① 函数 与 轴交点坐标是 ;
② 当 时, 随 的增大而增大;当 时, 随 的增大而减小;
故答案为: ① ; ② , ;
( 4 )类比上述探究函数的图象与性质的过程,画出函数 , , 的图象,
由函数图象知函数 的图象的性质:
① 函数 与 轴交点坐标是 ;
② 当 时, 随 的增大而减小;当 时, 随 的增大而增大;
故答案为: ① 函数 与 轴交点坐标是 ;
② 当 时, 随 的增大而减小;当 时, 随 的增大而增大.
( 5 )令 , ,
解得: , ,
∴ 若函数值 ,
∴ 可得 ,
故答案为: .
【点睛】
本题考查了一次函数的图象与性质,一次函数图象上点的坐标特征.正确画出函数的图象,利用数形结合思想是解题的关键.
同课章节目录
