沪科版数学九年级上册 第23章 解直角三角形23.2 解直角三角形(课件)(共16张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 第23章 解直角三角形23.2 解直角三角形(课件)(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 143.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
解直角三角形
(2)两锐角之间的关系:
∠A+∠B=90°
(3)边角之间的关系:
(1)三边之间的关系:
(勾股定理)
A
B
a
b
c
C
回顾与思考
C
A
B
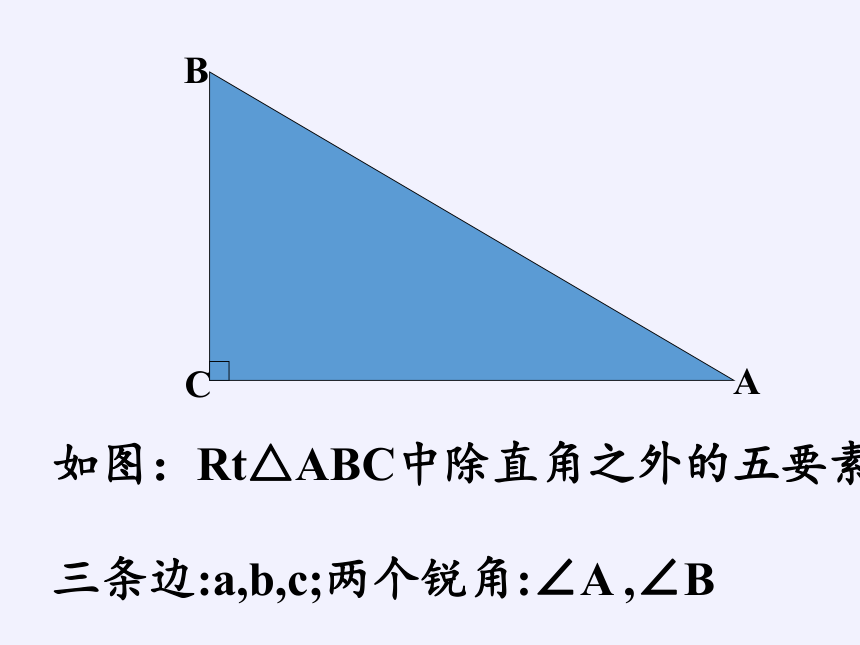
如图:Rt△ABC中除直角之外的五要素:
三条边:a,b,c;两个锐角:∠A ,∠B
A
C
B
a
b
c
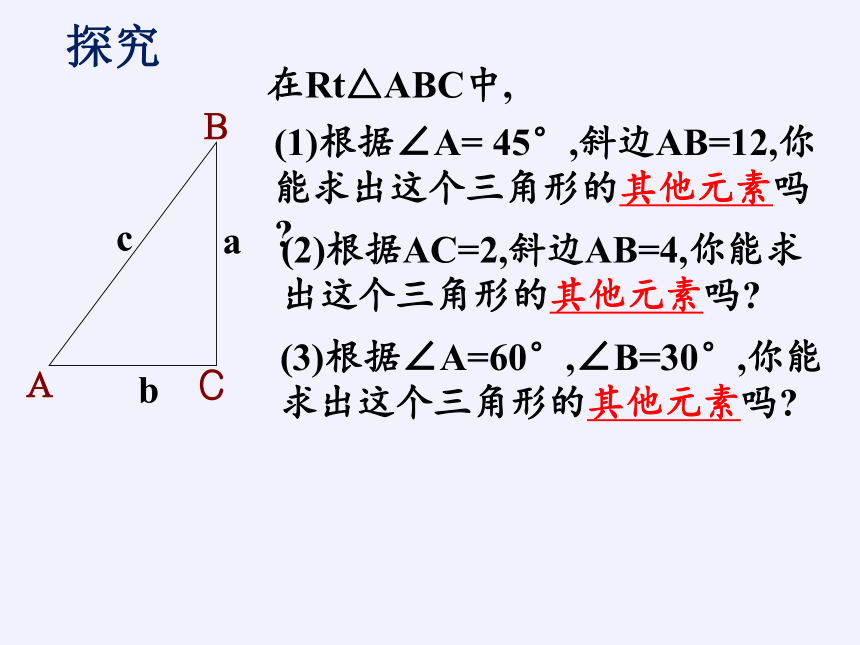
在Rt△ABC中,
(1)根据∠A= 45°,斜边AB=12,你能求出这个三角形的其他元素吗
(2)根据AC=2,斜边AB=4,你能求出这个三角形的其他元素吗
(3)根据∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗
探究
C
A
B
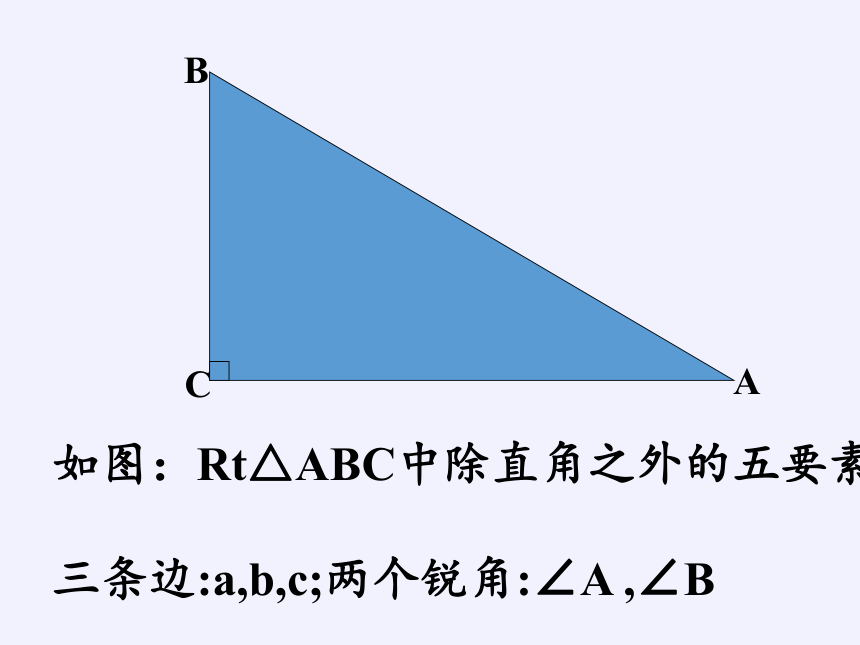
如图:Rt△ABC中除直角之外的五要素:
三条边:a,b,c;两个锐角:∠A ,∠B
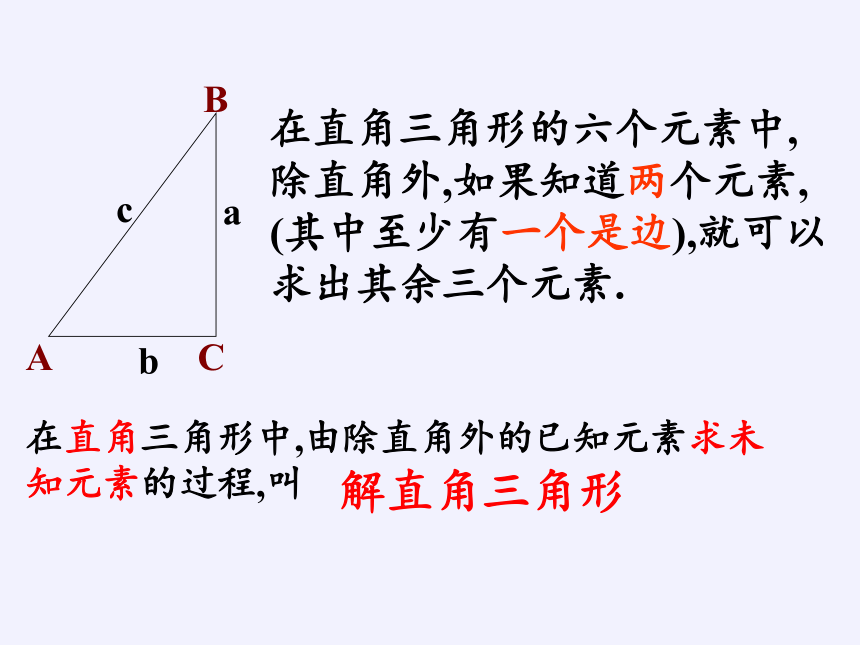
在直角三角形的六个元素中,除直角外,如果知道两个元素, (其中至少有一个是边),就可以求出其余三个元素.
在直角三角形中,由除直角外的已知元素求未知元素的过程,叫
解直角三角形
A
C
B
a
b
c
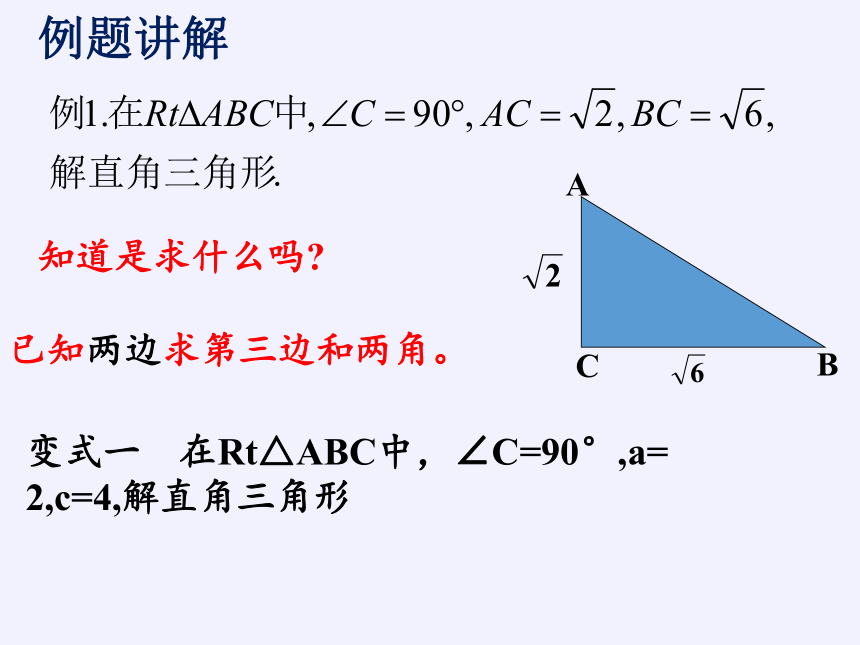
知道是求什么吗
A
C
B
已知两边求第三边和两角。
变式一 在Rt△ABC中,∠C=90°,a= 2,c=4,解直角三角形
例题讲解
知道是求什么吗
A
C
B
已知一边和一角求第三边和角。
变式二 在Rt△ABC中,∠C=90°, ∠B=30° AB= , 解直角三角形
问题: 春节时小明和爸爸妈妈一起挂灯笼,梯子与地面所成的角a一般要满足50°≤a≤75°. 问:
(1)妈妈拿了6m的梯子,使灯笼挂的最高为多少米?
(2)6米梯子底部距墙2·4米?这时人是否能够安全使用这个梯子?
(3)我要当老师:设计一个相关问题同学们互相解决。
解决问题
由 得
问题(1)可以归结为:在Rt △ABC中,已知
∠A=75°,斜边AB=6,求∠A的对边BC的长.
问题(1)当梯子与地面所成的角a为75°时,梯子顶端与地面的距离是使用这个梯子所能攀到的最大高度.
因此使用这个梯子能够安全攀到墙面的最大高度约是5.8m
所以 BC≈6×0.97≈5.8
由计算器求得 sin75°≈0.97
A
B
α
C
解:
对于问题(2),当梯子底端距离墙面2.4m时,求梯子与地面所成的角a的问题,
可以归结为:在Rt△ABC中,已知AC=2.4,斜边AB=6,求锐角a的度数
由于
利用计算器求得
a≈66°
因此当梯子底墙距离墙面2.4m时,梯子与地面
所成的角大约是66°
由50°<66°<75°可知,这时使用这个梯子是安全的.
A
B
C
α
解:
在△ABC中,∠A=55°,b=20cm,c=30cm。求三角形的面积S△ABC。
A
C
B
D
解:作AB边上的高CD,在Rt△ACD中
CD=AC·sinA=bsinA
当∠A=550,b=20cm,c=30cm时,有
中考再现
在△ABC中, ∠B=60°, ∠C=45°, AB=2
(1)求AC的值。
(2)求△ABC的周长与面积
B
A
C
D
中考演练
解直角
三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数
关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
归纳小结
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
作业
在Rt△ABC 中,∠C=90°,根据下列条件解直角三角形;
(1) c = 30 , b = 15
(2) ∠B=60°,c = 14
A
B
C
b=15
c
A
B
C
b
a
c=14
谢 谢
解直角三角形
(2)两锐角之间的关系:
∠A+∠B=90°
(3)边角之间的关系:
(1)三边之间的关系:
(勾股定理)
A
B
a
b
c
C
回顾与思考
C
A
B
如图:Rt△ABC中除直角之外的五要素:
三条边:a,b,c;两个锐角:∠A ,∠B
A
C
B
a
b
c
在Rt△ABC中,
(1)根据∠A= 45°,斜边AB=12,你能求出这个三角形的其他元素吗
(2)根据AC=2,斜边AB=4,你能求出这个三角形的其他元素吗
(3)根据∠A=60°,∠B=30°,你能求出这个三角形的其他元素吗
探究
C
A
B
如图:Rt△ABC中除直角之外的五要素:
三条边:a,b,c;两个锐角:∠A ,∠B
在直角三角形的六个元素中,除直角外,如果知道两个元素, (其中至少有一个是边),就可以求出其余三个元素.
在直角三角形中,由除直角外的已知元素求未知元素的过程,叫
解直角三角形
A
C
B
a
b
c
知道是求什么吗
A
C
B
已知两边求第三边和两角。
变式一 在Rt△ABC中,∠C=90°,a= 2,c=4,解直角三角形
例题讲解
知道是求什么吗
A
C
B
已知一边和一角求第三边和角。
变式二 在Rt△ABC中,∠C=90°, ∠B=30° AB= , 解直角三角形
问题: 春节时小明和爸爸妈妈一起挂灯笼,梯子与地面所成的角a一般要满足50°≤a≤75°. 问:
(1)妈妈拿了6m的梯子,使灯笼挂的最高为多少米?
(2)6米梯子底部距墙2·4米?这时人是否能够安全使用这个梯子?
(3)我要当老师:设计一个相关问题同学们互相解决。
解决问题
由 得
问题(1)可以归结为:在Rt △ABC中,已知
∠A=75°,斜边AB=6,求∠A的对边BC的长.
问题(1)当梯子与地面所成的角a为75°时,梯子顶端与地面的距离是使用这个梯子所能攀到的最大高度.
因此使用这个梯子能够安全攀到墙面的最大高度约是5.8m
所以 BC≈6×0.97≈5.8
由计算器求得 sin75°≈0.97
A
B
α
C
解:
对于问题(2),当梯子底端距离墙面2.4m时,求梯子与地面所成的角a的问题,
可以归结为:在Rt△ABC中,已知AC=2.4,斜边AB=6,求锐角a的度数
由于
利用计算器求得
a≈66°
因此当梯子底墙距离墙面2.4m时,梯子与地面
所成的角大约是66°
由50°<66°<75°可知,这时使用这个梯子是安全的.
A
B
C
α
解:
在△ABC中,∠A=55°,b=20cm,c=30cm。求三角形的面积S△ABC。
A
C
B
D
解:作AB边上的高CD,在Rt△ACD中
CD=AC·sinA=bsinA
当∠A=550,b=20cm,c=30cm时,有
中考再现
在△ABC中, ∠B=60°, ∠C=45°, AB=2
(1)求AC的值。
(2)求△ABC的周长与面积
B
A
C
D
中考演练
解直角
三角形
∠A+ ∠ B=90°
a2+b2=c2
三角函数
关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
归纳小结
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
作业
在Rt△ABC 中,∠C=90°,根据下列条件解直角三角形;
(1) c = 30 , b = 15
(2) ∠B=60°,c = 14
A
B
C
b=15
c
A
B
C
b
a
c=14
谢 谢
