2021-2022学年高一下学期物理人教版(2019)必修第二册5.2《运动的合成与分解》课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期物理人教版(2019)必修第二册5.2《运动的合成与分解》课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 84.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-29 09:39:48 | ||
图片预览








文档简介
(共23张PPT)
5.2 运动的合成与分解
复习上一节《曲线运动》
直线运动 曲线运动
轨迹
速度 方向
大小
加速度 (合外力) 方向
大小
分类
合力与速度方向
沿轨迹
沿轨迹上该点的切线方向
V=0 变或不变均可
V≠0 变或不变均可
沿轨迹
指向轨迹的凹侧
a=0 变或不变均可
a≠0 变或不变均可
a不变—匀变速直线运动
a变—变加速直线运动
a不变—匀变速曲线运动
a变—变加速曲线运动
共线:同向加速、反向减速
不共线:锐角加速、钝角减速
迷你实验室:合运动轨迹探究
感受合运动与分运动
1.将放有红蜡块的玻璃管倒置在水平的电动滑轨上,向右匀速运动,则红蜡块的运动轨迹是怎样的呢?
水平向右的匀速直线运动
探究实验:蜡块在玻璃管中的运动
2 .将玻璃管中注满清水并倒放静置,则红蜡块的运动轨迹是怎样的呢?
竖直向上的匀速直线运动
探究实验:蜡块在玻璃管中的运动
3 .将玻璃管中注满清水,并倒置在电动滑轨上,则红蜡块的运动轨迹是怎样的呢?
探究实验:蜡块在玻璃管中的运动
建立平面直角坐标系:以红蜡块刚开始运动时的位置为坐标原点O,水平向右为轴,
O
竖直向上为轴。
理论分析:蜡块在玻璃管中的运动
O
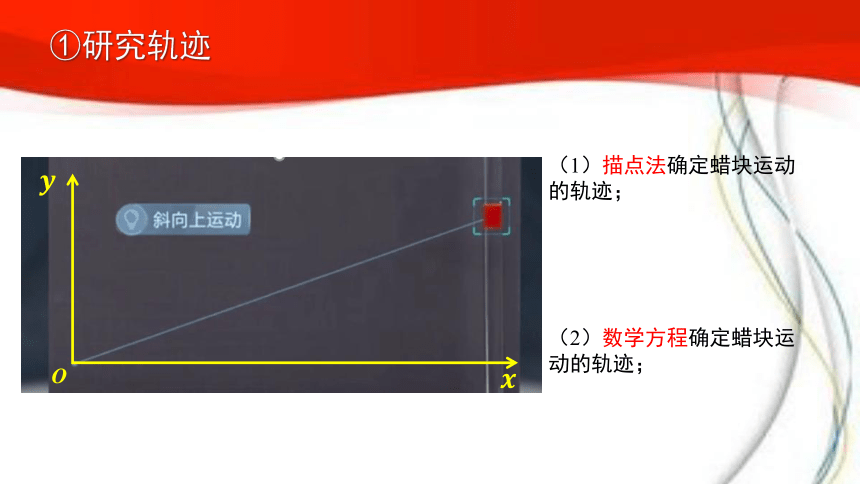
(2)数学方程确定蜡块运动的轨迹;
①研究轨迹
(1)描点法确定蜡块运动的轨迹;
O
②研究速度
O
③研究加速度
红蜡块同时参与了两个运动,一个是水平方向的匀速直线运动,一个是竖直方向的匀速直线运动,但最终是斜向右上方运动,故我们将水平和竖直的两个运动称为分运动;最终的运动称为合运动。
已知分运动,求解合运动的过程称为运动的合成;
已知合运动,求解分运动的过程称为运动的分解;
运动的合成和分解都遵循矢量运算法则(平行四边形法则)
概念形成:合运动与分运动
(一)合运动与分运动
如果一个物体同时参与了几个运动而形成了一个实际运动,那么:
物体实际所做的运动叫做合运动
同时参与的几个运动叫做分运动
什么是合运动与分运动
(二)合运动与分运动的关系
合运动与分运动的关系
等效性
合运动分运动效果相同
A
等时性
合运动分运动时间相同
B
独立性
分运动彼此独立,互不影响
C
匀速直线运动和匀加速直线运动的合运动
还是直线运动吗?
不共线的两个匀加速直线运动的合运动
是直线运动还是曲线运动呢?
a1
v1
a1
v1
①两个初速度为0 的匀加速直线运动
②两个初速度不为0 的匀变速直线运动
匀变速直线运动
a2
v2
v
a2
v2
v
a
匀变速曲线运动
a
初速度为0的匀加速直线运动
动手实验
从你的铅笔盒里取一块橡皮,用一根细线拴住,把细线的另一端用图钉固定在竖直放置的木板上.按图所示的方法,用铅笔靠着细线的左侧,沿直尺向右匀速移动,再向左移动,来回做几次,仔细观察橡皮的运动轨迹.
结合实验现象说明:橡皮的实际运动与哪两个方向的运动有关?
练习
1.(多选)如图甲所示,在杂技表演中,猴子沿竖直杆向上运动,其v t图象如图乙所示,同时人顶杆沿水平地面运动的x t图象如图丙所示。若以地面为参考系,下列说法中正确的是( )
A.猴子的运动轨迹为直线
B.猴子在2 s内做匀变速曲线运动
C.t=0时猴子的速度大小为8 m/s
D.t=2 s时猴子的加速度大小为4 m/s2
BD
练习
2.(多选)(2005上海)如图所示的塔吊臂上有一可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩.在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时,吊钩将物体B向上吊起,A、B之间的距离以d=H-2t2(SI)(SI表示国际单位制,式中H为吊臂离地面的高度)规律变化,则物体做( )
(A)速度大小不变的曲线运动
(B)速度大小增加的曲线运动
(C)加速度大小方向均不变的曲线运动
(D)加速度大小方向均变化的曲线运动
BC
练习
3. 关于两个运动的合运动,下列说法中正确的是( )
A.两个直线运动的合运动一定是直线运动
B.两个互成角度的匀速直线运动的合运动一定是匀速直线运动
C.两个互成角度的匀变速直线运动的合运动一定是匀变速直线运动
D.两个分运动的时间和它们的合运动的时间不相等
B
4.设玻璃管长l=1m,当玻璃管静止时,蜡块上升的加速度为0.5m/s2(蜡块初速度为零),现使玻璃管以水平速度0.5m/s匀速向右运动,当蜡块上升至玻璃管顶部时,求:
(1)蜡块的运动时间;(2)蜡块位移大小.
O
x
y
解:
(1)根据运动的独立性,
蜡块的运动时间为:
(2)2s内玻璃管的位移:
蜡块的位移:
练习
学以致用
利用今天所学,你能作出正确的判断吗?
橄榄射剑
01
总结你的收获
02
完成作业
03
记下你的问题
布置任务
5.2 运动的合成与分解
复习上一节《曲线运动》
直线运动 曲线运动
轨迹
速度 方向
大小
加速度 (合外力) 方向
大小
分类
合力与速度方向
沿轨迹
沿轨迹上该点的切线方向
V=0 变或不变均可
V≠0 变或不变均可
沿轨迹
指向轨迹的凹侧
a=0 变或不变均可
a≠0 变或不变均可
a不变—匀变速直线运动
a变—变加速直线运动
a不变—匀变速曲线运动
a变—变加速曲线运动
共线:同向加速、反向减速
不共线:锐角加速、钝角减速
迷你实验室:合运动轨迹探究
感受合运动与分运动
1.将放有红蜡块的玻璃管倒置在水平的电动滑轨上,向右匀速运动,则红蜡块的运动轨迹是怎样的呢?
水平向右的匀速直线运动
探究实验:蜡块在玻璃管中的运动
2 .将玻璃管中注满清水并倒放静置,则红蜡块的运动轨迹是怎样的呢?
竖直向上的匀速直线运动
探究实验:蜡块在玻璃管中的运动
3 .将玻璃管中注满清水,并倒置在电动滑轨上,则红蜡块的运动轨迹是怎样的呢?
探究实验:蜡块在玻璃管中的运动
建立平面直角坐标系:以红蜡块刚开始运动时的位置为坐标原点O,水平向右为轴,
O
竖直向上为轴。
理论分析:蜡块在玻璃管中的运动
O
(2)数学方程确定蜡块运动的轨迹;
①研究轨迹
(1)描点法确定蜡块运动的轨迹;
O
②研究速度
O
③研究加速度
红蜡块同时参与了两个运动,一个是水平方向的匀速直线运动,一个是竖直方向的匀速直线运动,但最终是斜向右上方运动,故我们将水平和竖直的两个运动称为分运动;最终的运动称为合运动。
已知分运动,求解合运动的过程称为运动的合成;
已知合运动,求解分运动的过程称为运动的分解;
运动的合成和分解都遵循矢量运算法则(平行四边形法则)
概念形成:合运动与分运动
(一)合运动与分运动
如果一个物体同时参与了几个运动而形成了一个实际运动,那么:
物体实际所做的运动叫做合运动
同时参与的几个运动叫做分运动
什么是合运动与分运动
(二)合运动与分运动的关系
合运动与分运动的关系
等效性
合运动分运动效果相同
A
等时性
合运动分运动时间相同
B
独立性
分运动彼此独立,互不影响
C
匀速直线运动和匀加速直线运动的合运动
还是直线运动吗?
不共线的两个匀加速直线运动的合运动
是直线运动还是曲线运动呢?
a1
v1
a1
v1
①两个初速度为0 的匀加速直线运动
②两个初速度不为0 的匀变速直线运动
匀变速直线运动
a2
v2
v
a2
v2
v
a
匀变速曲线运动
a
初速度为0的匀加速直线运动
动手实验
从你的铅笔盒里取一块橡皮,用一根细线拴住,把细线的另一端用图钉固定在竖直放置的木板上.按图所示的方法,用铅笔靠着细线的左侧,沿直尺向右匀速移动,再向左移动,来回做几次,仔细观察橡皮的运动轨迹.
结合实验现象说明:橡皮的实际运动与哪两个方向的运动有关?
练习
1.(多选)如图甲所示,在杂技表演中,猴子沿竖直杆向上运动,其v t图象如图乙所示,同时人顶杆沿水平地面运动的x t图象如图丙所示。若以地面为参考系,下列说法中正确的是( )
A.猴子的运动轨迹为直线
B.猴子在2 s内做匀变速曲线运动
C.t=0时猴子的速度大小为8 m/s
D.t=2 s时猴子的加速度大小为4 m/s2
BD
练习
2.(多选)(2005上海)如图所示的塔吊臂上有一可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩.在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时,吊钩将物体B向上吊起,A、B之间的距离以d=H-2t2(SI)(SI表示国际单位制,式中H为吊臂离地面的高度)规律变化,则物体做( )
(A)速度大小不变的曲线运动
(B)速度大小增加的曲线运动
(C)加速度大小方向均不变的曲线运动
(D)加速度大小方向均变化的曲线运动
BC
练习
3. 关于两个运动的合运动,下列说法中正确的是( )
A.两个直线运动的合运动一定是直线运动
B.两个互成角度的匀速直线运动的合运动一定是匀速直线运动
C.两个互成角度的匀变速直线运动的合运动一定是匀变速直线运动
D.两个分运动的时间和它们的合运动的时间不相等
B
4.设玻璃管长l=1m,当玻璃管静止时,蜡块上升的加速度为0.5m/s2(蜡块初速度为零),现使玻璃管以水平速度0.5m/s匀速向右运动,当蜡块上升至玻璃管顶部时,求:
(1)蜡块的运动时间;(2)蜡块位移大小.
O
x
y
解:
(1)根据运动的独立性,
蜡块的运动时间为:
(2)2s内玻璃管的位移:
蜡块的位移:
练习
学以致用
利用今天所学,你能作出正确的判断吗?
橄榄射剑
01
总结你的收获
02
完成作业
03
记下你的问题
布置任务
