2021-2022学年人教版九年级数学上册24.2.2 直线与圆的位置关系 同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册24.2.2 直线与圆的位置关系 同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 364.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 08:42:09 | ||
图片预览

文档简介
2021——2022学年度人教版九年级数学上册 第二十四章 圆
24.2.2 直线与圆的位置关系 同步练习
一、选择题
1.如果和内含,圆心距,的半径长是,那么的半径的取值范围是( ).
A. B. C. D.或
2.下列说法,正确的是( )
A.等弦所对的圆周角相等
B.弦所对的两条弧的中点的连线垂直平分弦,且过圆心
C.切线垂直于圆的半径
D.平分弦的直径垂直于弦
3.《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,同勾中 容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为步,股(长直角边)长为步,问该直角三角形内切圆的直径是多少步?”该问题的答案是( )
A. B. C. D.
4.如图,AB是⊙O的直径,C,D是⊙O上的点,,过点C作⊙O的切线交AB的延长线于点E,则等于( )
A. B. C. D.
5.如图,⊙O 是四边形 ABCD 的内切圆,连接 OA、OB、OC、OD.若∠AOB=110°,则∠COD 的度数是( )
A.60° B.70° C.80° D.45°
6.如图,在平行四边形中,,点,在上,点在上,,则的度数为( )
A.112.5° B.120° C.135° D.150°
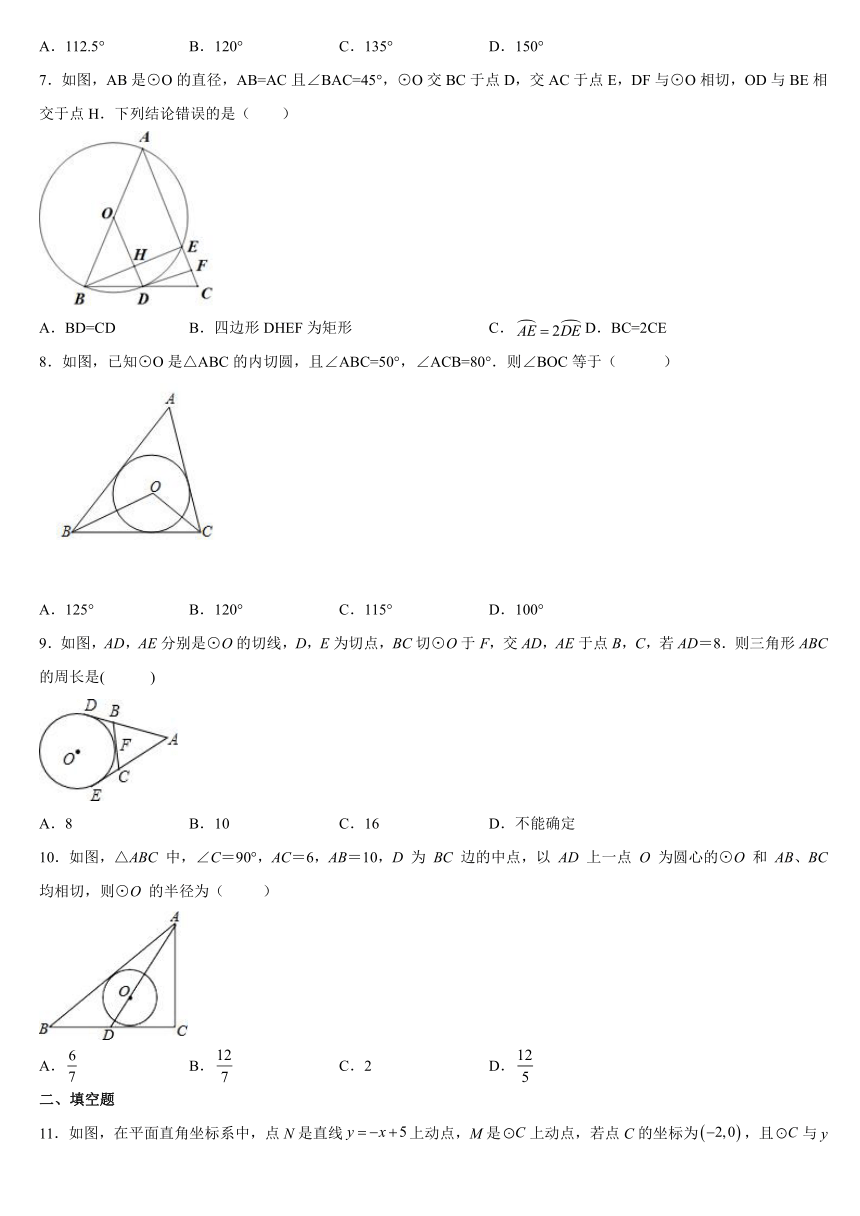
7.如图,AB是⊙O的直径,AB=AC且∠BAC=45°,⊙O交BC于点D,交AC于点E,DF与⊙O相切,OD与BE相交于点H.下列结论错误的是( )
A.BD=CD B.四边形DHEF为矩形 C. D.BC=2CE
8.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°.则∠BOC等于( )
A.125° B.120° C.115° D.100°
9.如图,AD,AE分别是⊙O的切线,D,E为切点,BC切⊙O于F,交AD,AE于点B,C,若AD=8.则三角形ABC的周长是( )
A.8 B.10 C.16 D.不能确定
10.如图,△ABC 中,∠C=90°,AC=6,AB=10,D 为 BC 边的中点,以 AD 上一点 O 为圆心的⊙O 和 AB、BC 均相切,则⊙O 的半径为( )
A. B. C.2 D.
二、填空题
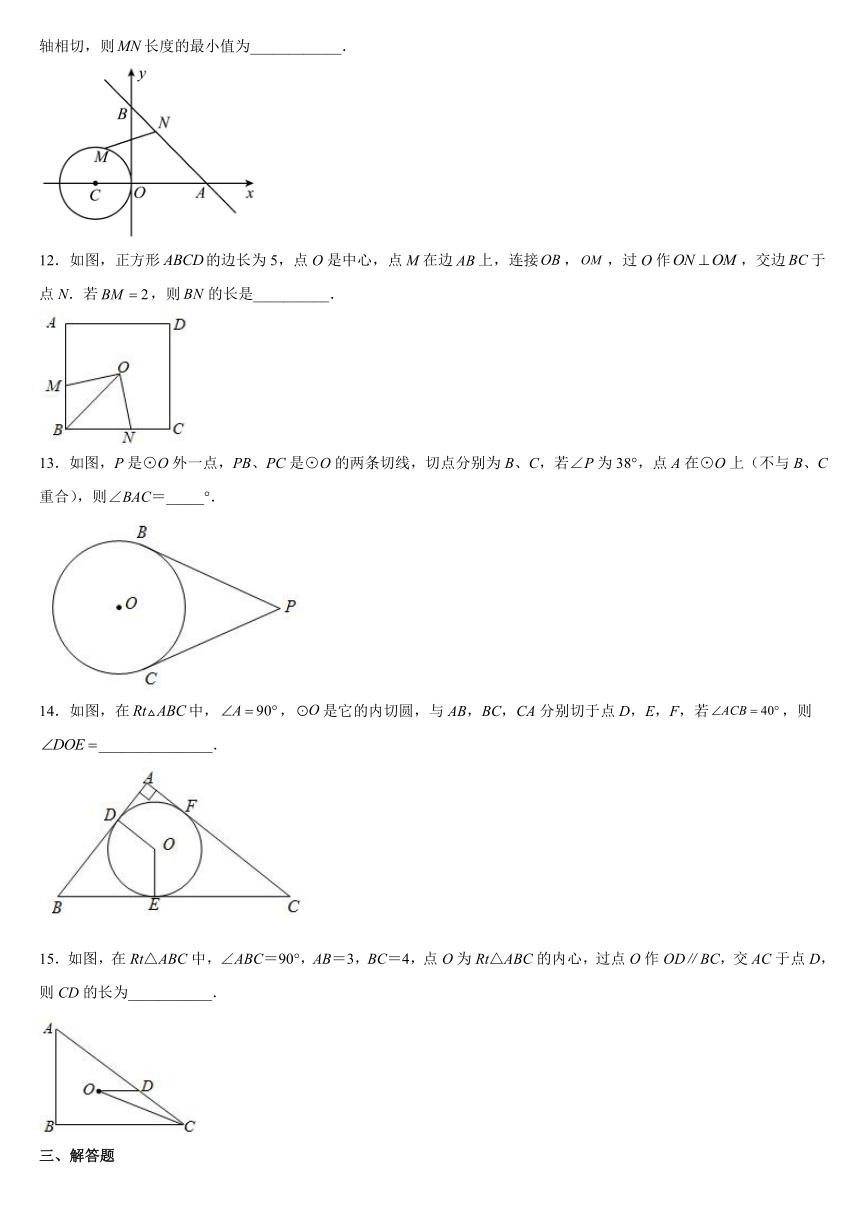
11.如图,在平面直角坐标系中,点N是直线上动点,M是上动点,若点C的坐标为,且与y轴相切,则长度的最小值为____________.
12.如图,正方形的边长为5,点O是中心,点M在边上,连接,,过O作,交边于点N.若,则的长是__________.
13.如图,P是⊙O外一点,PB、PC是⊙O的两条切线,切点分别为B、C,若∠P为38°,点A在⊙O上(不与B、C重合),则∠BAC=_____°.
14.如图,在中,,是它的内切圆,与AB,BC,CA分别切于点D,E,F,若,则_______________.
15.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,点O为Rt△ABC的内心,过点O作OD∥BC,交AC于点D,则CD的长为___________.
三、解答题
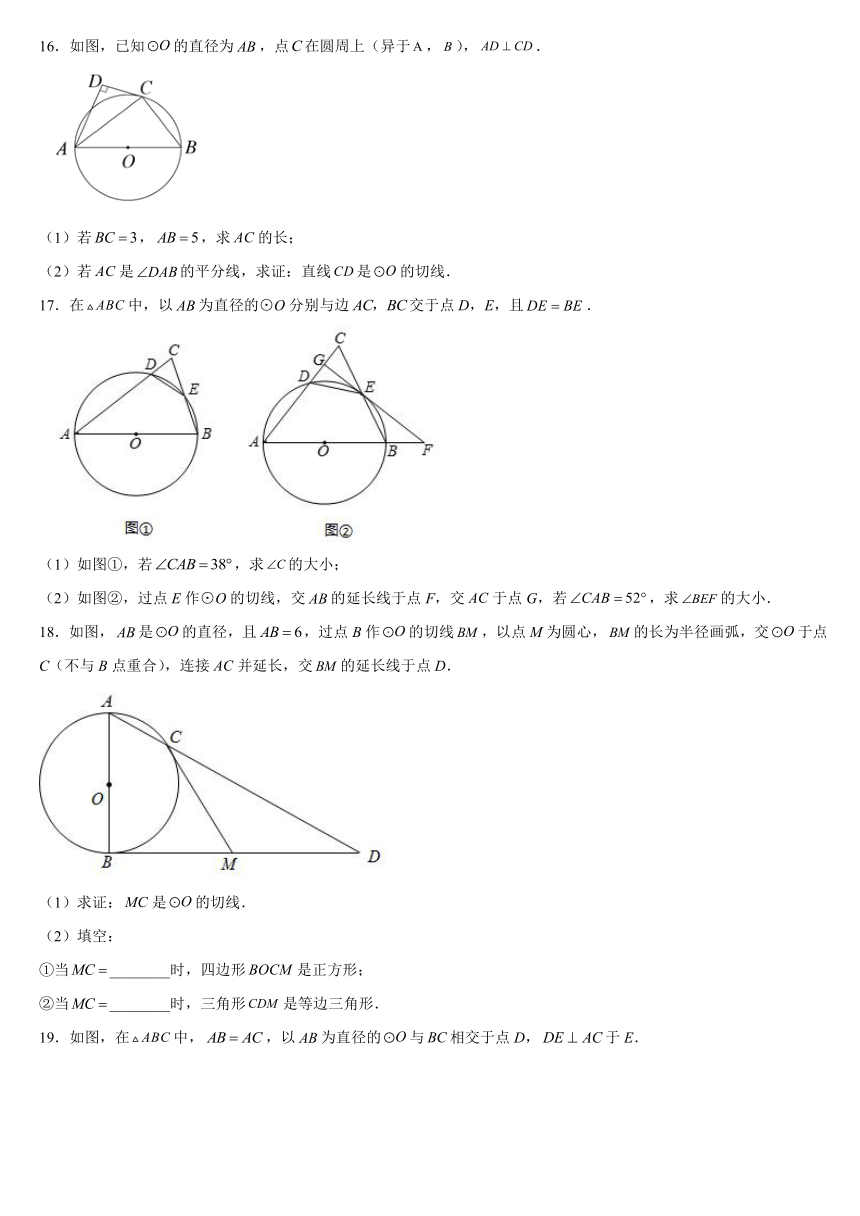
16.如图,已知的直径为,点在圆周上(异于,),.
(1)若,,求的长;
(2)若是的平分线,求证:直线是的切线.
17.在中,以为直径的⊙O分别与边交于点D,E,且.
(1)如图①,若,求的大小;
(2)如图②,过点E作⊙O的切线,交的延长线于点F,交于点G,若,求的大小.
18.如图,是的直径,且,过点B作的切线,以点M为圆心,的长为半径画弧,交于点C(不与B点重合),连接并延长,交的延长线于点D.
(1)求证:是的切线.
(2)填空:
①当________时,四边形是正方形;
②当________时,三角形是等边三角形.
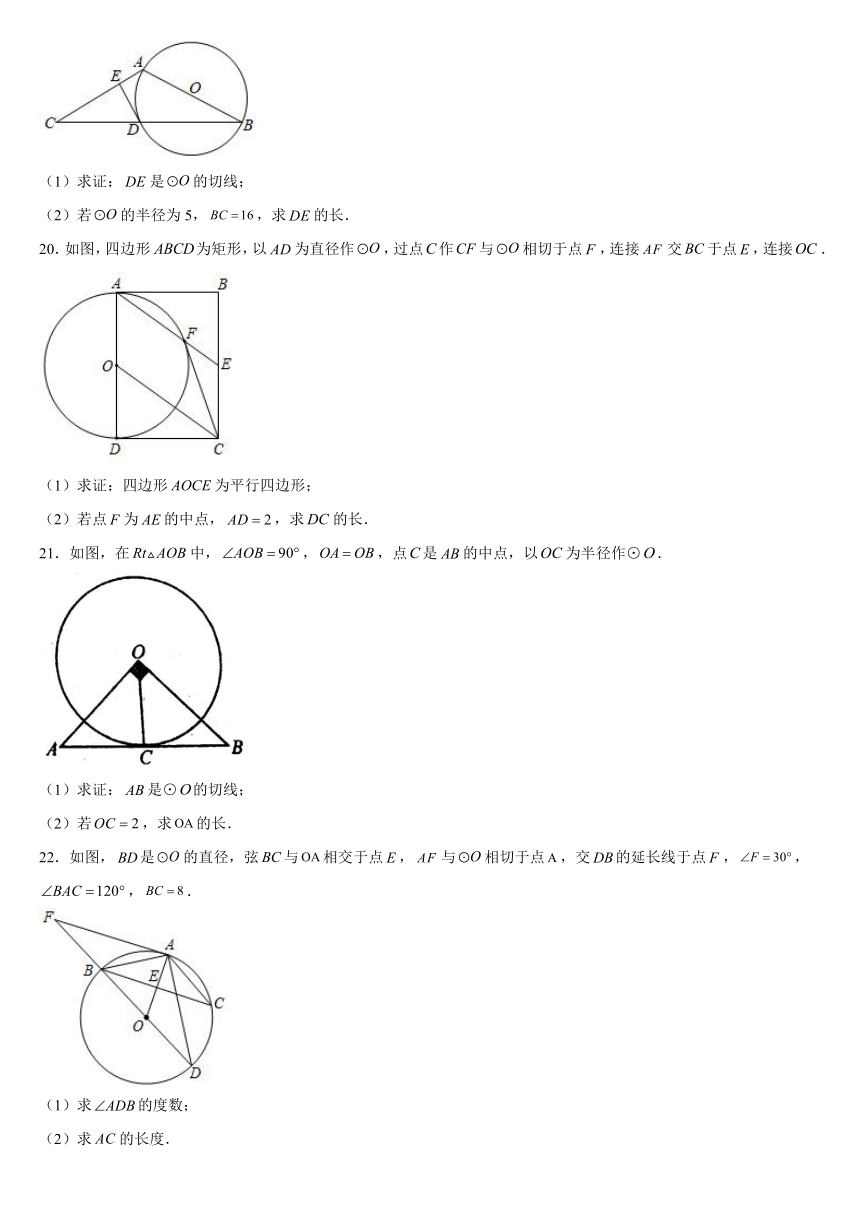
19.如图,在中,,以为直径的与相交于点D,于E.
(1)求证:是的切线;
(2)若的半径为5,,求的长.
20.如图,四边形为矩形,以为直径作,过点作与相切于点,连接交于点,连接.
(1)求证:四边形为平行四边形;
(2)若点为的中点,,求的长.
21.如图,在中,,,点是的中点,以为半径作⊙.
(1)求证:是⊙的切线;
(2)若,求的长.
22.如图,是的直径,弦与相交于点,与相切于点,交的延长线于点,,,.
(1)求的度数;
(2)求的长度.
(3)判定四边形的形状,并证明你的结论.
23.小锐同学是一个数学学习爱好者,他在一本数学课外读物上看到一个课本上没有的与圆相关的角---弦切角(弦切角的定义:把顶点在圆上,一边与圆相切,另一边和圆相交的角叫做弦切角),并尝试用所学的知识研究弦切角的有关性质.
(1)如图,直线与⊙O相切于点,,为⊙O上不同于的两点,连接,,.请你写出图中的两个弦切角______;(不添加新的字母和线段)
(2)小锐目测和可能相等,并通过测量的方法验证了他的结论,你能帮小锐用几何推理的方法证明结论的正确性吗?
已知:如图,直线与⊙O相切于点,,为圆上不同于的两点,连接,,.
求证:.
如果我们把上述结论称为弦切角定理,请你用一句话概括弦切角定理______.
【参考答案】
1.D 2.B 3.D 4.B 5.B 6.C 7.D 8.C 9.C 10.B
11.-2
12.3
13.71或109
14.130°
15.
16.(1)证明:为直径
,,
∴根据勾股定理可得:;
∴AC的长为4.
(2)证明:连结,
,
是的角平分线,
,
∴∠D+∠DCO=180°,
,
∴∠D=90°,
∴∠DCO=90°,
∴直线是的切线.
17.解:(Ⅰ)如图,连接.
∵ ,
∴ .
∴ .
∵ ,
∴ .
∵ 为⊙的直径,
∴ .
∴ .
(2)如图,连接,.
∵ 为⊙的切线,
∴ .
∵ ,
∴ .
∴ .
∵ ,
∴ .
∴ .
18.(1)证明:连接、,如图所示.
∵是的切线,
∴.
在和中,
,
∴.
∴.
∴是的切线.
(2)①当MC=3时,四边形BOCM是正方形,理由如下:
∵,
又,
∴.
∴.
∴四边形是菱形.
∵,
∴四边形是正方形.
故答案为3;
②当时,三角形是等边三角形,理由如下,
∵,,
∴.
∴.
∴.
∴.
∴.
∴.
∵,
∴.
∴.
∴,
∴.
∴是等边三角形.
故答案为.
19.(1)证明:连接.
∵,
∴
∵,
∴
∴
∴OD//AC
∵
∴
∵是圆的半径,
∴是的切线;
(2)连接,
∵为的直径,
∴,即,
∵,,
∴
∵的半径为5
∴,
∴,
∵,
∴,
∴.
20.(1)如图,连接DF、OF,DF交于G,
∵AD为直径,
∴∠AFD=90°,
∵与相切于点,
∴∠OFC=90°,
∵四边形为矩形,
∴∠ADC=∠DAB=90°,OA//CE,
∴DC是切线,
∴DC=CF,
∵OD=OF,
∴OC是线段DF的垂直平分线,
∴∠OGD=90°,
∴OC//AE,
∴四边形AOCE是平行四边形.
(2)如图,连接OE、OF,
∵AD=2,OA=OD,
∴OF=OA=1,
∵四边形AOCE是平行四边形,
∴OA=CE,
∵AD=BC,
∴OA=BE,
∵OA//BE,
∴四边形AOEB是平行四边形,
∵∠DAB=90°,
∴四边形AOEB是矩形,
∴∠AOE=90°,OE=AB=DC,
∵F为AE中点,
∴AE=2OF=2,
∴DC=OE===.
21.(1)证明:∵,点是的中点,
∴,
∵为的半径,
∴是的切线;
(2)∵是等腰直角三角形,点是的中点,
∴,,
∵,
∴.
22.解:(1)∵AF与⊙O相切于点A,
∴AF⊥OA,
∵∠F=30°,
∴∠AOF=60°,
∵OA=OD,∠AOF=∠ADB+∠OAD,
∴∠ADB=∠OAD=30°;
(2)∵∠ACB=∠ADB=30°,∠BAC=120°,
∴∠ABC=180°-120°-30°=30°,
∴∠ABC=∠ACB,
∴AB=AC,
∴,
∴OA⊥BC,
∴BE=CE=BC=4,
∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴AB=OB,
∵∠OBE=30°,
∴OE=OB,BE=OE=4,
∴OE=,
∴AC=AB=OB=2OE=;
(3)四边形AFBC是平行四边形.理由如下:
∵AF⊥OA,OA⊥BC,
∴AF∥BC,
∵∠OBE=30°,∠ACB=∠ADB=30°,
∴∠OBE=∠ACB=30°,
∴BF∥AC,
∴四边形AFBC是平行四边形.
23.解:(1)弦CD、CE分别与切线CB构成的弦切角为:∠DCB,∠ECB;
弦CD、CE分别与切线CA构成的弦切角为:∠DCA,∠ECA.
故答案为:,,,(任意写2个即可)
(2)证明:过作直径,连接.
∵是直径,
∴.
∴.
又∵与相切于点,
∴.
∴.
∴.
∴.
∴.
(3)弦切角等于它所夹的弧所对的圆周角.
24.2.2 直线与圆的位置关系 同步练习
一、选择题
1.如果和内含,圆心距,的半径长是,那么的半径的取值范围是( ).
A. B. C. D.或
2.下列说法,正确的是( )
A.等弦所对的圆周角相等
B.弦所对的两条弧的中点的连线垂直平分弦,且过圆心
C.切线垂直于圆的半径
D.平分弦的直径垂直于弦
3.《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,同勾中 容圆径几何.”其意思为:“今有直角三角形,勾(短直角边)长为步,股(长直角边)长为步,问该直角三角形内切圆的直径是多少步?”该问题的答案是( )
A. B. C. D.
4.如图,AB是⊙O的直径,C,D是⊙O上的点,,过点C作⊙O的切线交AB的延长线于点E,则等于( )
A. B. C. D.
5.如图,⊙O 是四边形 ABCD 的内切圆,连接 OA、OB、OC、OD.若∠AOB=110°,则∠COD 的度数是( )
A.60° B.70° C.80° D.45°
6.如图,在平行四边形中,,点,在上,点在上,,则的度数为( )
A.112.5° B.120° C.135° D.150°
7.如图,AB是⊙O的直径,AB=AC且∠BAC=45°,⊙O交BC于点D,交AC于点E,DF与⊙O相切,OD与BE相交于点H.下列结论错误的是( )
A.BD=CD B.四边形DHEF为矩形 C. D.BC=2CE
8.如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°.则∠BOC等于( )
A.125° B.120° C.115° D.100°
9.如图,AD,AE分别是⊙O的切线,D,E为切点,BC切⊙O于F,交AD,AE于点B,C,若AD=8.则三角形ABC的周长是( )
A.8 B.10 C.16 D.不能确定
10.如图,△ABC 中,∠C=90°,AC=6,AB=10,D 为 BC 边的中点,以 AD 上一点 O 为圆心的⊙O 和 AB、BC 均相切,则⊙O 的半径为( )
A. B. C.2 D.
二、填空题
11.如图,在平面直角坐标系中,点N是直线上动点,M是上动点,若点C的坐标为,且与y轴相切,则长度的最小值为____________.
12.如图,正方形的边长为5,点O是中心,点M在边上,连接,,过O作,交边于点N.若,则的长是__________.
13.如图,P是⊙O外一点,PB、PC是⊙O的两条切线,切点分别为B、C,若∠P为38°,点A在⊙O上(不与B、C重合),则∠BAC=_____°.
14.如图,在中,,是它的内切圆,与AB,BC,CA分别切于点D,E,F,若,则_______________.
15.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,点O为Rt△ABC的内心,过点O作OD∥BC,交AC于点D,则CD的长为___________.
三、解答题
16.如图,已知的直径为,点在圆周上(异于,),.
(1)若,,求的长;
(2)若是的平分线,求证:直线是的切线.
17.在中,以为直径的⊙O分别与边交于点D,E,且.
(1)如图①,若,求的大小;
(2)如图②,过点E作⊙O的切线,交的延长线于点F,交于点G,若,求的大小.
18.如图,是的直径,且,过点B作的切线,以点M为圆心,的长为半径画弧,交于点C(不与B点重合),连接并延长,交的延长线于点D.
(1)求证:是的切线.
(2)填空:
①当________时,四边形是正方形;
②当________时,三角形是等边三角形.
19.如图,在中,,以为直径的与相交于点D,于E.
(1)求证:是的切线;
(2)若的半径为5,,求的长.
20.如图,四边形为矩形,以为直径作,过点作与相切于点,连接交于点,连接.
(1)求证:四边形为平行四边形;
(2)若点为的中点,,求的长.
21.如图,在中,,,点是的中点,以为半径作⊙.
(1)求证:是⊙的切线;
(2)若,求的长.
22.如图,是的直径,弦与相交于点,与相切于点,交的延长线于点,,,.
(1)求的度数;
(2)求的长度.
(3)判定四边形的形状,并证明你的结论.
23.小锐同学是一个数学学习爱好者,他在一本数学课外读物上看到一个课本上没有的与圆相关的角---弦切角(弦切角的定义:把顶点在圆上,一边与圆相切,另一边和圆相交的角叫做弦切角),并尝试用所学的知识研究弦切角的有关性质.
(1)如图,直线与⊙O相切于点,,为⊙O上不同于的两点,连接,,.请你写出图中的两个弦切角______;(不添加新的字母和线段)
(2)小锐目测和可能相等,并通过测量的方法验证了他的结论,你能帮小锐用几何推理的方法证明结论的正确性吗?
已知:如图,直线与⊙O相切于点,,为圆上不同于的两点,连接,,.
求证:.
如果我们把上述结论称为弦切角定理,请你用一句话概括弦切角定理______.
【参考答案】
1.D 2.B 3.D 4.B 5.B 6.C 7.D 8.C 9.C 10.B
11.-2
12.3
13.71或109
14.130°
15.
16.(1)证明:为直径
,,
∴根据勾股定理可得:;
∴AC的长为4.
(2)证明:连结,
,
是的角平分线,
,
∴∠D+∠DCO=180°,
,
∴∠D=90°,
∴∠DCO=90°,
∴直线是的切线.
17.解:(Ⅰ)如图,连接.
∵ ,
∴ .
∴ .
∵ ,
∴ .
∵ 为⊙的直径,
∴ .
∴ .
(2)如图,连接,.
∵ 为⊙的切线,
∴ .
∵ ,
∴ .
∴ .
∵ ,
∴ .
∴ .
18.(1)证明:连接、,如图所示.
∵是的切线,
∴.
在和中,
,
∴.
∴.
∴是的切线.
(2)①当MC=3时,四边形BOCM是正方形,理由如下:
∵,
又,
∴.
∴.
∴四边形是菱形.
∵,
∴四边形是正方形.
故答案为3;
②当时,三角形是等边三角形,理由如下,
∵,,
∴.
∴.
∴.
∴.
∴.
∴.
∵,
∴.
∴.
∴,
∴.
∴是等边三角形.
故答案为.
19.(1)证明:连接.
∵,
∴
∵,
∴
∴
∴OD//AC
∵
∴
∵是圆的半径,
∴是的切线;
(2)连接,
∵为的直径,
∴,即,
∵,,
∴
∵的半径为5
∴,
∴,
∵,
∴,
∴.
20.(1)如图,连接DF、OF,DF交于G,
∵AD为直径,
∴∠AFD=90°,
∵与相切于点,
∴∠OFC=90°,
∵四边形为矩形,
∴∠ADC=∠DAB=90°,OA//CE,
∴DC是切线,
∴DC=CF,
∵OD=OF,
∴OC是线段DF的垂直平分线,
∴∠OGD=90°,
∴OC//AE,
∴四边形AOCE是平行四边形.
(2)如图,连接OE、OF,
∵AD=2,OA=OD,
∴OF=OA=1,
∵四边形AOCE是平行四边形,
∴OA=CE,
∵AD=BC,
∴OA=BE,
∵OA//BE,
∴四边形AOEB是平行四边形,
∵∠DAB=90°,
∴四边形AOEB是矩形,
∴∠AOE=90°,OE=AB=DC,
∵F为AE中点,
∴AE=2OF=2,
∴DC=OE===.
21.(1)证明:∵,点是的中点,
∴,
∵为的半径,
∴是的切线;
(2)∵是等腰直角三角形,点是的中点,
∴,,
∵,
∴.
22.解:(1)∵AF与⊙O相切于点A,
∴AF⊥OA,
∵∠F=30°,
∴∠AOF=60°,
∵OA=OD,∠AOF=∠ADB+∠OAD,
∴∠ADB=∠OAD=30°;
(2)∵∠ACB=∠ADB=30°,∠BAC=120°,
∴∠ABC=180°-120°-30°=30°,
∴∠ABC=∠ACB,
∴AB=AC,
∴,
∴OA⊥BC,
∴BE=CE=BC=4,
∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,
∴AB=OB,
∵∠OBE=30°,
∴OE=OB,BE=OE=4,
∴OE=,
∴AC=AB=OB=2OE=;
(3)四边形AFBC是平行四边形.理由如下:
∵AF⊥OA,OA⊥BC,
∴AF∥BC,
∵∠OBE=30°,∠ACB=∠ADB=30°,
∴∠OBE=∠ACB=30°,
∴BF∥AC,
∴四边形AFBC是平行四边形.
23.解:(1)弦CD、CE分别与切线CB构成的弦切角为:∠DCB,∠ECB;
弦CD、CE分别与切线CA构成的弦切角为:∠DCA,∠ECA.
故答案为:,,,(任意写2个即可)
(2)证明:过作直径,连接.
∵是直径,
∴.
∴.
又∵与相切于点,
∴.
∴.
∴.
∴.
∴.
(3)弦切角等于它所夹的弧所对的圆周角.
同课章节目录
