2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.3.2抛物线简单几何性质(2)课件(21张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册3.3.2抛物线简单几何性质(2)课件(21张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 16:57:13 | ||
图片预览







文档简介
(共21张PPT)
空白演示
单击输入您的封面副标题
3.3.2 抛物线的简单几何性质
第二课时
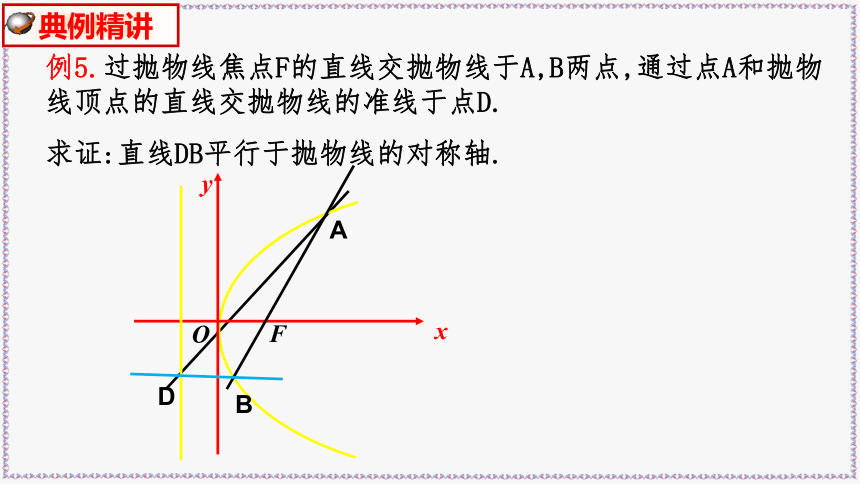
例5.过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D.
求证:直线DB平行于抛物线的对称轴.
O
x
y
F
A
B
D
典例精讲
例5 过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴。
O
x
y
F
A
B
D
例6.如图所示,已知定点,轴于点,是线段上任意一点,于点,与相交于点,求点的轨迹方程。
解:设点,,其中,则点的坐
标为.
由题意,直线的方程为 ①
因为点在上,将点的坐标带入①,得
②
所以点的横坐标满足②
直线的方程为, ③
因为点在上,所以点的坐标满足③
典例精讲
将②代入③,消去,得即点的轨迹方程。
1.求适合下列条件的抛物线的标准方程:
(1)焦点F关于准线的对称点为M(0,一9);
(2)关于y轴对称,与直线y=-12相交所得线段的长为12;
(3)关于x轴对称,以焦点和准线上的两点为顶点的三角形是边长为的等边三角形.
2.点M(m,4)在抛物线y2=24x上,F为焦点,直线MF与准线相交于点N,求|FN|.
3.设抛物线x2=2py(p>0)上的点M与焦点F的距离为4,点M到y轴的距离为,求抛物线的方程和点M的坐标.
课堂练习
课本P138 练习 第1、2、3题
4.两条直线y=kx和y= - kx分别与抛物线y2=2px(p>0)相交于不同于原点的A,B两点,k为何值时,直线AB经过抛物线的焦点
5.已知圆心在y轴上移动的圆经过点A(0,5),且与x轴、y轴分别交于B(x,0),C(0,y)两个动点,求点M(x,y)的轨迹方程.
课堂练习
课本P138 练习 第4、5题
抛物线的性质(补充)
直线与抛物线的位置关系
椭圆与直线的位置关系及判断方法
<0
=0
>0
(1)联立方程组
(2)消去一个未知数,得一个一元二次方程
(3)
相离
相切
相交
复习旧知
x
y
O
x
y
O
相离:0个交点
相交:一个交点
相交:两个交点
相切:一个交点
双曲线与直线的位置关系及交点个数
复习旧知
判断直线与双曲线位置关系的步骤
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
复习旧知
直线与抛物线位置关系
x
y
O
1.相离(没有交点)
2.相切(一个交点)
3.相交(一个交点,两个交点)
与双曲线的情况一样
探究新知
判断直线与抛物线位置关系的操作程序(一)
把直线方程代入抛物线方程
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行(重合)
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
探究新知
判断直线是否与抛物线的对称轴平行
不平行
直线与抛物线相交(一个交点)
平行
判断直线与抛物线位置关系的操作程序(二)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
探究新知
典例精讲
已知抛物线方程为y2=4x,直线l过定点P(-2,1),斜率k,
k为何值时,直线l与抛物线y2=4x:
⑴只有一个公共点; ⑵有两个公共点; ⑶没有公共点
过点M(0,1)和抛物线C:y2=4x 仅有一个公共点的直线的方程是__________________________.
巩固练习
若k=0,则直线方程为y=1
解:若直线斜率不存在,直线方程为x=0
若直线斜率存在,设直线方程为y=kx+1
若k0,由=16-16k=0,得k=1
则直线方程为y=x+1
空白演示
单击输入您的封面副标题
3.3.2 抛物线的简单几何性质
第二课时
例5.过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D.
求证:直线DB平行于抛物线的对称轴.
O
x
y
F
A
B
D
典例精讲
例5 过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴。
O
x
y
F
A
B
D
例6.如图所示,已知定点,轴于点,是线段上任意一点,于点,与相交于点,求点的轨迹方程。
解:设点,,其中,则点的坐
标为.
由题意,直线的方程为 ①
因为点在上,将点的坐标带入①,得
②
所以点的横坐标满足②
直线的方程为, ③
因为点在上,所以点的坐标满足③
典例精讲
将②代入③,消去,得即点的轨迹方程。
1.求适合下列条件的抛物线的标准方程:
(1)焦点F关于准线的对称点为M(0,一9);
(2)关于y轴对称,与直线y=-12相交所得线段的长为12;
(3)关于x轴对称,以焦点和准线上的两点为顶点的三角形是边长为的等边三角形.
2.点M(m,4)在抛物线y2=24x上,F为焦点,直线MF与准线相交于点N,求|FN|.
3.设抛物线x2=2py(p>0)上的点M与焦点F的距离为4,点M到y轴的距离为,求抛物线的方程和点M的坐标.
课堂练习
课本P138 练习 第1、2、3题
4.两条直线y=kx和y= - kx分别与抛物线y2=2px(p>0)相交于不同于原点的A,B两点,k为何值时,直线AB经过抛物线的焦点
5.已知圆心在y轴上移动的圆经过点A(0,5),且与x轴、y轴分别交于B(x,0),C(0,y)两个动点,求点M(x,y)的轨迹方程.
课堂练习
课本P138 练习 第4、5题
抛物线的性质(补充)
直线与抛物线的位置关系
椭圆与直线的位置关系及判断方法
<0
=0
>0
(1)联立方程组
(2)消去一个未知数,得一个一元二次方程
(3)
相离
相切
相交
复习旧知
x
y
O
x
y
O
相离:0个交点
相交:一个交点
相交:两个交点
相切:一个交点
双曲线与直线的位置关系及交点个数
复习旧知
判断直线与双曲线位置关系的步骤
把直线方程代入双曲线方程
得到一元一次方程
得到一元二次方程
直线与双曲线的
渐进线平行
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
复习旧知
直线与抛物线位置关系
x
y
O
1.相离(没有交点)
2.相切(一个交点)
3.相交(一个交点,两个交点)
与双曲线的情况一样
探究新知
判断直线与抛物线位置关系的操作程序(一)
把直线方程代入抛物线方程
得到一元一次方程
得到一元二次方程
直线与抛物线的
对称轴平行(重合)
相交(一个交点)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
探究新知
判断直线是否与抛物线的对称轴平行
不平行
直线与抛物线相交(一个交点)
平行
判断直线与抛物线位置关系的操作程序(二)
计 算 判 别 式
>0
=0
<0
相交
相切
相离
探究新知
典例精讲
已知抛物线方程为y2=4x,直线l过定点P(-2,1),斜率k,
k为何值时,直线l与抛物线y2=4x:
⑴只有一个公共点; ⑵有两个公共点; ⑶没有公共点
过点M(0,1)和抛物线C:y2=4x 仅有一个公共点的直线的方程是__________________________.
巩固练习
若k=0,则直线方程为y=1
解:若直线斜率不存在,直线方程为x=0
若直线斜率存在,设直线方程为y=kx+1
若k0,由=16-16k=0,得k=1
则直线方程为y=x+1
