期末整理复习(试题)数学三年级下册(无答案)青岛版
文档属性
| 名称 | 期末整理复习(试题)数学三年级下册(无答案)青岛版 |  | |
| 格式 | zip | ||
| 文件大小 | 418.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 10:48:29 | ||
图片预览



文档简介
三年级下册数学期末整理与复习
说明:下面是归类整理了本学期的重点、难点、知识和方法,利用了提纲的形式呈现,便于家长和学生的理解,不是为了让孩子单纯做题的,而是帮助孩子复习的,所以请家长们监督孩子好好利用复习资料,对照整理复习的知识点和例题,帮助学生回顾一下原来课堂上总结的一些思路和方法,然后仿照着在上面出1-2道类似的题目加以巩固练习。
(请同学们准备好以下学习用品:练习本、直尺、量角器、一副三角尺)
一、万以上数的认识
1.一(个)、十、百、千、万、十万、百万、千万、亿……都是( )。每相邻的两个计数单位之间的进率都是( ),这种计数方法叫( )计数法。
2.按照我国的计数习惯,从右边起,每( )个数位是一级。( )是个级;( )是万级;( )是亿级。
3.多位数的读法:从( )位读起,一级一级地往下读;读亿级或万级数时,要按照( )数的读法来读,再在后面加一个“亿”字或“万”字;每级末尾的0( ),其他数位有一个0或连续有几个0都只读( )个“零”。
4.多位数的写法:从( )位写起,一级一级的往下写;哪个数位上一个单位也没有,就在那个数位上写( )。
5.万以上数的大小比较:先看( ),位数多的数就大;位数相同,再从最( )位看起,相同数位上的数大,那个数就大。
6.数的改写:改写成用“万”作单位的数:把万位后面的( )个0去掉,加上一个( )字;改写成用“亿”作单位的数:把亿位后面的( )个0去掉,加上一个( )字。
7.近似数:一个数与精确数相近(比精确数略多或略少),这个数称为( )。
用( )法求近似数:先根据要求确定看哪个数位,再根据数位上数的大小确定是“舍”还是“入”。
改写只改变书写的形式,数的大小( ),用( )连接;求近似数,数的大小( ),用( )连接。
8.数不仅可以用来表示( )和( ),还可以来( )。(书23页)
二、小数的初步认识
1.小数的意义:像0.1、0.4、0.55、1.2……这样的数,都是小数。
( )的分数可以写成一位小数,( )的分数可以写成两位小数。
2.小数的读法:整数部分按照整数的读法来读,小数点读作“点”,小数部分通常顺次读出每一个数位上的数字(像读电话号码一样)。
3.小数的写法:整数部分按照整数的写法来写,(整数部分是零的写作“0”),小数点写在个位右下角,小数部分顺次写出每一个数位上的数字。
4.一位小数的大小比较:先看它们的( )部分,( )部分大的那个数就大;整数部分相同的,再比较小数点后第一位小数,第一位小数大的这个小数就大。
5.一位小数的加减法:先把各数的( )对齐,(也就是把相同数位上的数对齐),再按照整数加、减法的法则进行计算,最后点上小数点。
三、年月日
1.24时计时法
①区分12时计时法和24时计时法
12时计时法:
24时计时法:
②两种计时法互相转换的方法:
12时计时法→24时计时法:
24时计时法→12时计时法:
2.计算经过的时间(首先区分“时刻”与“时间段”)
①亮亮每天上午7:55到校上学,中午11:30放学,上午在校时间有多长?
②他中午11:45到家,下午2:10离开家去上学,中午在家时间有多长?
③他每天晚上8:30睡觉,到次日6:30分起床。睡眠时间多长?
④一节课40分钟,上午8:25上第一节课,什么时间下课?
⑤一节课40分钟,下午3:20下第一节课,什么时间开始上课?
⑥2014年上半年2月20日开学,7月10日开始放假。本学期一共有多少天?
3. 年月日
一年有( )个月。 大月有 ,每个月有( )天;小月有 ,每个月有( )天; ( )月既不是大月,也不是小月,平年有( )天,闰年有( )天。
一年有( )天的年份是平年,一年有( )天的年份是闰年。公历年份是( )的倍数的,一般是闰年;但公历年份是整百数的,必须是( )的倍数才是闰年。
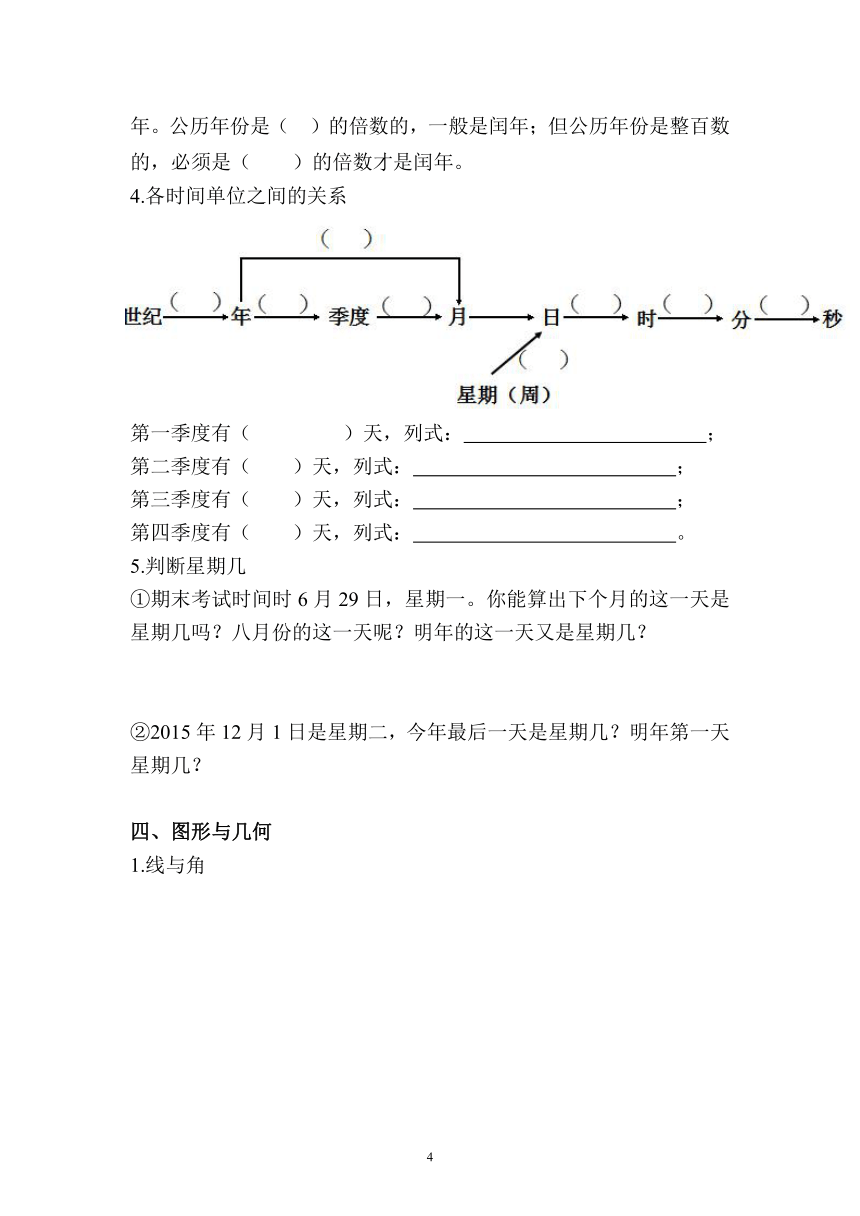
4.各时间单位之间的关系
第一季度有( )天,列式: ;
第二季度有( )天,列式: ;
第三季度有( )天,列式: ;
第四季度有( )天,列式: 。
5.判断星期几
①期末考试时间时6月29日,星期一。你能算出下个月的这一天是星期几吗?八月份的这一天呢?明年的这一天又是星期几?
②2015年12月1日是星期二,今年最后一天是星期几?明年第一天星期几?
四、图形与几何
1.线与角
画图 特点
线段
射线
直线
角 从一点引出两条( )所组成的图形叫做角。
(1)
线段、射线、直线之间的 联系: 和 都是 的一部分。
过一点可以画( )条射线,过一点可以画( )条直线,过两点可以画( )条直线。
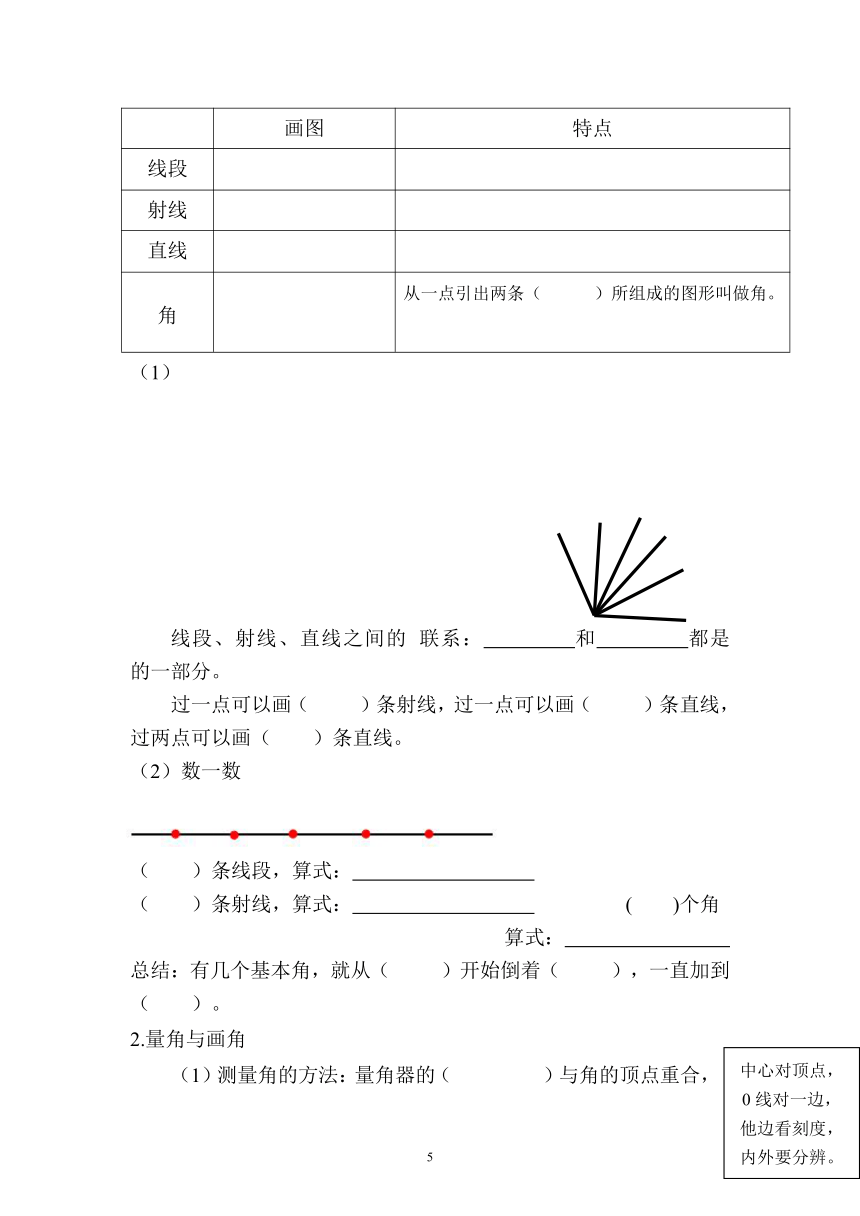
(2)数一数
( )条线段,算式:
( )条射线,算式: ( )个角
算式:
总结:有几个基本角,就从( )开始倒着( ),一直加到( )。
2.量角与画角
(1)测量角的方法:量角器的( )与角的顶点重合,( )和角的一条边重合,另一条边指在量角器上的度数就是这个角的度数。在读刻度时要( )。
(2)画角的方法:先画一条射线,接着把量角器的( )与射线的( )重合,( )和射线重合,对准相应的度数画一个点,然后从射线的( )起,通过所画的点再画出一条( )。
(3)以A为顶点画一个40°的角,
以B为顶点画一个50°的角,
组成一个三角形,并量出这个
三角形第三个角的度数。
(4)三角尺上的角
①标出三角尺上各角的度数
②用一副三角尺可以画出哪些角?试着画一画。
(5)角的分类
①从小到大依次为: 、 、 、 、 。
1平角=( )直角,1周角=( )平角=( )直角
②求下面各角的度数
∠ =90°,是直角;
∠2= ,是 ;
∠3= ,是 .
3.平行与相交
(1)在同一平面内,两条直线的位置关系有( )和( )。
在同一平面内( )的两条直线互相平行,其中一条直线是另一条直线的( )。
两条直线相交成90°时,这两条直线互相( ),其中一条直线是另一条直线的( ),两条直线的交点叫作( )。
(2)画平行线和垂线(方法参照《平行线与垂线的画法》PPT演示)
①过A点,画出已知直线的平行线 ②过A点,画出已知直线的垂线
②过直线外一点可以画( )条已知直线的平行线;过直线上一点可以画( )条已知直线的垂线,过直线外一点可以画( )条已知直线的垂线。
4. 两点之间( )的长度最短,它的长度就是两点间的距离。
从直线外一点到这条直线所画的( )最短,它的长度叫作点到直线的距离。
5.( )后能够( )的图形是轴对称图形。
五、计算
1.三位数乘两位数
(1)口算:注意末尾需要添加几个0
(2)笔算
①笔算方法:用第二个因数的个位分别乘第一个因数的每一位,再用第二个因数的十位分别乘第一个因数的每一位,最后再把两个积相加。
②因数末尾有0的乘法
360×24= 470×30=
(3)估算:把一个因数或两个因数看作最接近的整十数或整百数相乘。
248×31≈7500 182×68≈1400 (要比较容易计算)
250 30 200 70
(4)积的变化规律
一个因数不变,另一个因数乘几,得到的积就等于原来的积也乘几。
一个因数不变,另一个因数除以几,得到的积就等于原来的积也除以几。
24×75=1800 35×12=420 18×4=72
48×75=( ) 35×6=( ) 180×40=( )
75×12=( ) 5×12=( ) 36×12=( )
2.两、三位数除以一位数
(1)口算
除数是整十数的口算:先将被除数和除数同时去掉一个0。
(2)估算
估算不需要计算出准确结果,先看除数接近几十,由此再确定被除数看作几百几十。
例:248÷32≈8 先把32看作30,因为三八二十四,所以把248看作240,而不是250
240 30
272÷68≈3 先把68看作70,因为四七二十八,所以把272看作280
280 70
(3)笔算
①判断商的位数:被除数前两位的数比除数大,商是( )位数;被除数前两位的数比除数小,商是( )位数。
例1.下面各题中的被除数都是三位数。(把对应的序号填在下面括号内)
①5□0÷60 ②70□÷68 ③40□÷42 ④6□0÷60
( )的商是两位数,( )的商是一位数。
例2.要使□35÷53的商是一位数,□中最大能填( );要使商是两位数,□中最小能填( )。
例3.要使454÷4□的商是两位数,□中最大能填( );要使商是一位数,□中最小能填( )。
②计算方法
除数是两位,先看( ),两位不够看三位,除到哪位商哪位,不够商1( )占位,余数要比除数( ),每次算完要比较。
③需要注意的两个竖式:
920÷40= 960÷12=
或者
(4)验算
没有余数的:( )×( )=被除数
有余数的:( )×( )+( )=被除数
(5)商不变的性质
被除数和除数( )乘或除以相同的数( 除外),( )不变。
51÷3=17 900÷50=18 100÷25=4
510÷30=( ) 90÷5=( ) 400÷25=( )
( )÷15=17 9000÷500=( ) 700÷25=( )
3.脱式计算
①在没有括号的混合运算中,只有一级运算时,( )依次计算。
②在没有括号的混合运算中,有两级运算时,应先算( )再算( )。
③在有小括号的混合运算中,要先算( ),小括号里有两级运算的要先算( )再算( )。
④在在一个算式中,既有小括号,又有中括号,要先算( ),再算( )。
4.列式计算
①从4000除以25的商里减去13 ②320减去17个8的和,所得的差
与12的积,差是多少? 乘18,积是多少?
③756除以18的商加上24,所得的和 ④580减去26乘5的积,再除以90,
的3倍是多少? 所得的商是多少?
六、解决问题
第一步、审题:认真读题,理解题目的意思,圈关键词、画线段图整理信息。
第二步、分析:用哪个数量关系式,或者先求什么再求什么。
第三步、解答:列综合算式时想清楚先算什么再算什么,是否要加括号;在草稿纸上列竖式保证计算正确!
第四步、检验:检查思路是否是都正确,有没有抄错数,回去再算一遍,或者换一种方法再做一遍。
单价 数量 总价
篮球 178元/个 15个
足球 85元/个 510元
羽毛球 16个 96元
例1.列式:
数量关系式:
速度 时间 路程
火车 140千米/时 12小时
汽车 12小时 900千米
步行 60米/分 720米
例2.列式:
数量关系式:
例3.相遇问题(先画图整理条件和问题,再解答)
(1)甲、乙两列火车分别从东、西两地同时相对开出,5小时后相遇。甲车速度是110千米/时,乙车速度是120千米/时。求东、西两地间的路程。
画图:
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
(2)甲、乙两个工程队从同一地点分别向东、西两个方向铺设管道。甲队每天铺设140米,乙队每天铺设150米。5天后,两队一共铺设管道多少米?
画图:
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
(3)小华和小亮在环形跑道上跑步,两人从同一地点同时出发,反向而行。小华每秒跑4米,小亮每秒跑6米,经过40秒两人相遇。环形跑道长多少米?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
(4)两人同时开始录入一份稿件,1小时正好录完。甲每分钟打80字,乙每分钟打65字。甲比乙多录入多少字?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
例4.水果店运来一些苹果,如果每箱装12千克,需要132个箱子。如果每箱装18千克,需要多少个箱子?
先求: 综合算式:
再求:
例5.火车2小时行驶240千米,从A城到B城需要12小时。A城到B城的铁路全长多少千米?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
例6.一块长方形草坪的面积是160平方米,要把宽由原来的8米增加到24米,长不变。扩大后草坪的面积是多少?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
例7.每个足球82元,每个排球64元。学校各买了25个,一共花了多少钱?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
例8.王阿姨去服装城批发了20件上衣和20条裤子。买上衣花了960元,买裤子花了780元.一件上衣比一条裤子贵多少钱?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
例9.公园有柳树36棵,杨树比柳树少12棵,槐树的棵树是柳树和杨树的总棵数的4倍。槐树有多少棵?
先求: 综合算式:
再求:
最后求:
例10.大鲸鱼重5.3吨,小鲸鱼重3.8吨。
①这两头鲸鱼共重多少吨? ②这两头鲸鱼相差多少吨?
例11.每袋饲料重46千克,买250袋。用载重9吨的小货车运,一次能运完吗?
例12.植树问题
(1)一座桥长180米,在桥的两边每隔12米装一盏路灯(两端都装),一共要装多少盏路灯?
(2)公园小路一侧有一排椅子,一共有50把椅子(起点和终点没有),没两把椅子之间相距8米。这条小路多少米?
中心对顶点,
0线对一边,
他边看刻度,
内外要分辨。
A
B
A
A
A
10
说明:下面是归类整理了本学期的重点、难点、知识和方法,利用了提纲的形式呈现,便于家长和学生的理解,不是为了让孩子单纯做题的,而是帮助孩子复习的,所以请家长们监督孩子好好利用复习资料,对照整理复习的知识点和例题,帮助学生回顾一下原来课堂上总结的一些思路和方法,然后仿照着在上面出1-2道类似的题目加以巩固练习。
(请同学们准备好以下学习用品:练习本、直尺、量角器、一副三角尺)
一、万以上数的认识
1.一(个)、十、百、千、万、十万、百万、千万、亿……都是( )。每相邻的两个计数单位之间的进率都是( ),这种计数方法叫( )计数法。
2.按照我国的计数习惯,从右边起,每( )个数位是一级。( )是个级;( )是万级;( )是亿级。
3.多位数的读法:从( )位读起,一级一级地往下读;读亿级或万级数时,要按照( )数的读法来读,再在后面加一个“亿”字或“万”字;每级末尾的0( ),其他数位有一个0或连续有几个0都只读( )个“零”。
4.多位数的写法:从( )位写起,一级一级的往下写;哪个数位上一个单位也没有,就在那个数位上写( )。
5.万以上数的大小比较:先看( ),位数多的数就大;位数相同,再从最( )位看起,相同数位上的数大,那个数就大。
6.数的改写:改写成用“万”作单位的数:把万位后面的( )个0去掉,加上一个( )字;改写成用“亿”作单位的数:把亿位后面的( )个0去掉,加上一个( )字。
7.近似数:一个数与精确数相近(比精确数略多或略少),这个数称为( )。
用( )法求近似数:先根据要求确定看哪个数位,再根据数位上数的大小确定是“舍”还是“入”。
改写只改变书写的形式,数的大小( ),用( )连接;求近似数,数的大小( ),用( )连接。
8.数不仅可以用来表示( )和( ),还可以来( )。(书23页)
二、小数的初步认识
1.小数的意义:像0.1、0.4、0.55、1.2……这样的数,都是小数。
( )的分数可以写成一位小数,( )的分数可以写成两位小数。
2.小数的读法:整数部分按照整数的读法来读,小数点读作“点”,小数部分通常顺次读出每一个数位上的数字(像读电话号码一样)。
3.小数的写法:整数部分按照整数的写法来写,(整数部分是零的写作“0”),小数点写在个位右下角,小数部分顺次写出每一个数位上的数字。
4.一位小数的大小比较:先看它们的( )部分,( )部分大的那个数就大;整数部分相同的,再比较小数点后第一位小数,第一位小数大的这个小数就大。
5.一位小数的加减法:先把各数的( )对齐,(也就是把相同数位上的数对齐),再按照整数加、减法的法则进行计算,最后点上小数点。
三、年月日
1.24时计时法
①区分12时计时法和24时计时法
12时计时法:
24时计时法:
②两种计时法互相转换的方法:
12时计时法→24时计时法:
24时计时法→12时计时法:
2.计算经过的时间(首先区分“时刻”与“时间段”)
①亮亮每天上午7:55到校上学,中午11:30放学,上午在校时间有多长?
②他中午11:45到家,下午2:10离开家去上学,中午在家时间有多长?
③他每天晚上8:30睡觉,到次日6:30分起床。睡眠时间多长?
④一节课40分钟,上午8:25上第一节课,什么时间下课?
⑤一节课40分钟,下午3:20下第一节课,什么时间开始上课?
⑥2014年上半年2月20日开学,7月10日开始放假。本学期一共有多少天?
3. 年月日
一年有( )个月。 大月有 ,每个月有( )天;小月有 ,每个月有( )天; ( )月既不是大月,也不是小月,平年有( )天,闰年有( )天。
一年有( )天的年份是平年,一年有( )天的年份是闰年。公历年份是( )的倍数的,一般是闰年;但公历年份是整百数的,必须是( )的倍数才是闰年。
4.各时间单位之间的关系
第一季度有( )天,列式: ;
第二季度有( )天,列式: ;
第三季度有( )天,列式: ;
第四季度有( )天,列式: 。
5.判断星期几
①期末考试时间时6月29日,星期一。你能算出下个月的这一天是星期几吗?八月份的这一天呢?明年的这一天又是星期几?
②2015年12月1日是星期二,今年最后一天是星期几?明年第一天星期几?
四、图形与几何
1.线与角
画图 特点
线段
射线
直线
角 从一点引出两条( )所组成的图形叫做角。
(1)
线段、射线、直线之间的 联系: 和 都是 的一部分。
过一点可以画( )条射线,过一点可以画( )条直线,过两点可以画( )条直线。
(2)数一数
( )条线段,算式:
( )条射线,算式: ( )个角
算式:
总结:有几个基本角,就从( )开始倒着( ),一直加到( )。
2.量角与画角
(1)测量角的方法:量角器的( )与角的顶点重合,( )和角的一条边重合,另一条边指在量角器上的度数就是这个角的度数。在读刻度时要( )。
(2)画角的方法:先画一条射线,接着把量角器的( )与射线的( )重合,( )和射线重合,对准相应的度数画一个点,然后从射线的( )起,通过所画的点再画出一条( )。
(3)以A为顶点画一个40°的角,
以B为顶点画一个50°的角,
组成一个三角形,并量出这个
三角形第三个角的度数。
(4)三角尺上的角
①标出三角尺上各角的度数
②用一副三角尺可以画出哪些角?试着画一画。
(5)角的分类
①从小到大依次为: 、 、 、 、 。
1平角=( )直角,1周角=( )平角=( )直角
②求下面各角的度数
∠ =90°,是直角;
∠2= ,是 ;
∠3= ,是 .
3.平行与相交
(1)在同一平面内,两条直线的位置关系有( )和( )。
在同一平面内( )的两条直线互相平行,其中一条直线是另一条直线的( )。
两条直线相交成90°时,这两条直线互相( ),其中一条直线是另一条直线的( ),两条直线的交点叫作( )。
(2)画平行线和垂线(方法参照《平行线与垂线的画法》PPT演示)
①过A点,画出已知直线的平行线 ②过A点,画出已知直线的垂线
②过直线外一点可以画( )条已知直线的平行线;过直线上一点可以画( )条已知直线的垂线,过直线外一点可以画( )条已知直线的垂线。
4. 两点之间( )的长度最短,它的长度就是两点间的距离。
从直线外一点到这条直线所画的( )最短,它的长度叫作点到直线的距离。
5.( )后能够( )的图形是轴对称图形。
五、计算
1.三位数乘两位数
(1)口算:注意末尾需要添加几个0
(2)笔算
①笔算方法:用第二个因数的个位分别乘第一个因数的每一位,再用第二个因数的十位分别乘第一个因数的每一位,最后再把两个积相加。
②因数末尾有0的乘法
360×24= 470×30=
(3)估算:把一个因数或两个因数看作最接近的整十数或整百数相乘。
248×31≈7500 182×68≈1400 (要比较容易计算)
250 30 200 70
(4)积的变化规律
一个因数不变,另一个因数乘几,得到的积就等于原来的积也乘几。
一个因数不变,另一个因数除以几,得到的积就等于原来的积也除以几。
24×75=1800 35×12=420 18×4=72
48×75=( ) 35×6=( ) 180×40=( )
75×12=( ) 5×12=( ) 36×12=( )
2.两、三位数除以一位数
(1)口算
除数是整十数的口算:先将被除数和除数同时去掉一个0。
(2)估算
估算不需要计算出准确结果,先看除数接近几十,由此再确定被除数看作几百几十。
例:248÷32≈8 先把32看作30,因为三八二十四,所以把248看作240,而不是250
240 30
272÷68≈3 先把68看作70,因为四七二十八,所以把272看作280
280 70
(3)笔算
①判断商的位数:被除数前两位的数比除数大,商是( )位数;被除数前两位的数比除数小,商是( )位数。
例1.下面各题中的被除数都是三位数。(把对应的序号填在下面括号内)
①5□0÷60 ②70□÷68 ③40□÷42 ④6□0÷60
( )的商是两位数,( )的商是一位数。
例2.要使□35÷53的商是一位数,□中最大能填( );要使商是两位数,□中最小能填( )。
例3.要使454÷4□的商是两位数,□中最大能填( );要使商是一位数,□中最小能填( )。
②计算方法
除数是两位,先看( ),两位不够看三位,除到哪位商哪位,不够商1( )占位,余数要比除数( ),每次算完要比较。
③需要注意的两个竖式:
920÷40= 960÷12=
或者
(4)验算
没有余数的:( )×( )=被除数
有余数的:( )×( )+( )=被除数
(5)商不变的性质
被除数和除数( )乘或除以相同的数( 除外),( )不变。
51÷3=17 900÷50=18 100÷25=4
510÷30=( ) 90÷5=( ) 400÷25=( )
( )÷15=17 9000÷500=( ) 700÷25=( )
3.脱式计算
①在没有括号的混合运算中,只有一级运算时,( )依次计算。
②在没有括号的混合运算中,有两级运算时,应先算( )再算( )。
③在有小括号的混合运算中,要先算( ),小括号里有两级运算的要先算( )再算( )。
④在在一个算式中,既有小括号,又有中括号,要先算( ),再算( )。
4.列式计算
①从4000除以25的商里减去13 ②320减去17个8的和,所得的差
与12的积,差是多少? 乘18,积是多少?
③756除以18的商加上24,所得的和 ④580减去26乘5的积,再除以90,
的3倍是多少? 所得的商是多少?
六、解决问题
第一步、审题:认真读题,理解题目的意思,圈关键词、画线段图整理信息。
第二步、分析:用哪个数量关系式,或者先求什么再求什么。
第三步、解答:列综合算式时想清楚先算什么再算什么,是否要加括号;在草稿纸上列竖式保证计算正确!
第四步、检验:检查思路是否是都正确,有没有抄错数,回去再算一遍,或者换一种方法再做一遍。
单价 数量 总价
篮球 178元/个 15个
足球 85元/个 510元
羽毛球 16个 96元
例1.列式:
数量关系式:
速度 时间 路程
火车 140千米/时 12小时
汽车 12小时 900千米
步行 60米/分 720米
例2.列式:
数量关系式:
例3.相遇问题(先画图整理条件和问题,再解答)
(1)甲、乙两列火车分别从东、西两地同时相对开出,5小时后相遇。甲车速度是110千米/时,乙车速度是120千米/时。求东、西两地间的路程。
画图:
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
(2)甲、乙两个工程队从同一地点分别向东、西两个方向铺设管道。甲队每天铺设140米,乙队每天铺设150米。5天后,两队一共铺设管道多少米?
画图:
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
(3)小华和小亮在环形跑道上跑步,两人从同一地点同时出发,反向而行。小华每秒跑4米,小亮每秒跑6米,经过40秒两人相遇。环形跑道长多少米?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
(4)两人同时开始录入一份稿件,1小时正好录完。甲每分钟打80字,乙每分钟打65字。甲比乙多录入多少字?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
例4.水果店运来一些苹果,如果每箱装12千克,需要132个箱子。如果每箱装18千克,需要多少个箱子?
先求: 综合算式:
再求:
例5.火车2小时行驶240千米,从A城到B城需要12小时。A城到B城的铁路全长多少千米?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
例6.一块长方形草坪的面积是160平方米,要把宽由原来的8米增加到24米,长不变。扩大后草坪的面积是多少?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
例7.每个足球82元,每个排球64元。学校各买了25个,一共花了多少钱?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
例8.王阿姨去服装城批发了20件上衣和20条裤子。买上衣花了960元,买裤子花了780元.一件上衣比一条裤子贵多少钱?
①先求: ②先求:
再求: 再求:
综合算式: 综合算式:
例9.公园有柳树36棵,杨树比柳树少12棵,槐树的棵树是柳树和杨树的总棵数的4倍。槐树有多少棵?
先求: 综合算式:
再求:
最后求:
例10.大鲸鱼重5.3吨,小鲸鱼重3.8吨。
①这两头鲸鱼共重多少吨? ②这两头鲸鱼相差多少吨?
例11.每袋饲料重46千克,买250袋。用载重9吨的小货车运,一次能运完吗?
例12.植树问题
(1)一座桥长180米,在桥的两边每隔12米装一盏路灯(两端都装),一共要装多少盏路灯?
(2)公园小路一侧有一排椅子,一共有50把椅子(起点和终点没有),没两把椅子之间相距8米。这条小路多少米?
中心对顶点,
0线对一边,
他边看刻度,
内外要分辨。
A
B
A
A
A
10
同课章节目录
