5.4.1正弦函数、余弦函数的图像 课件(共19页PPT)
文档属性
| 名称 | 5.4.1正弦函数、余弦函数的图像 课件(共19页PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 16:05:44 | ||
图片预览



文档简介
(共19张PPT)
5.4.1正、余弦函数图像
人教A(2019)版
九年级上册
新知导入
复习巩固
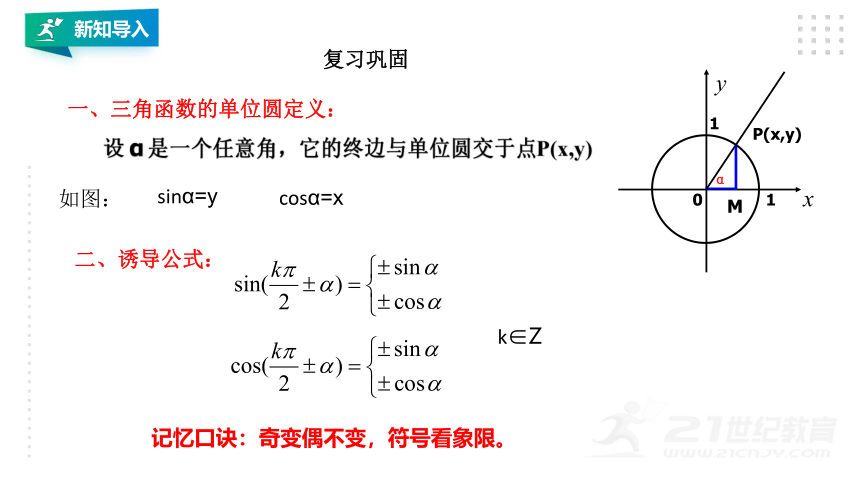
一、三角函数的单位圆定义:
设 α 是一个任意角,它的终边与单位圆交于点P(x,y)
0
1
1
P(x,y)
M
如图:
sinα=y
cosα=x
α
二、诱导公式:
k∈Z
记忆口诀:奇变偶不变,符号看象限。
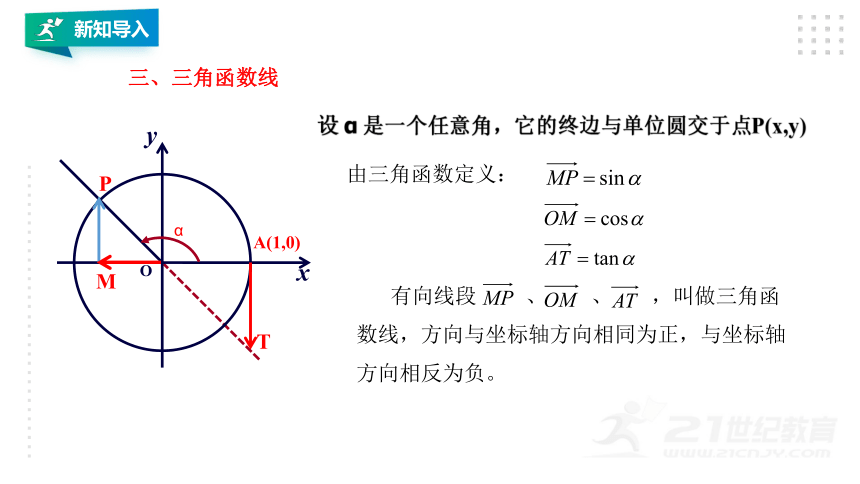
三、三角函数线
新知导入
M
P
O
y
x
A(1,0)
T
α
设 α 是一个任意角,它的终边与单位圆交于点P(x,y)
由三角函数定义:
有向线段 、 、 ,叫做三角函
数线,方向与坐标轴方向相同为正,与坐标轴
方向相反为负。
新知讲解
正弦函数、余弦函数的概念
任意给定一个实数x,有唯一确定的值sinx(或cosx)与之对应,
即:f:x→y=sinx(或f:x→y=cosx)
则由上述对应法则确定的函数叫正弦函数(或余弦函数)
正弦函数:y=sinx
余弦函数:y=cosx
由前面的知识我们知道,自变量x∈R,由以往研究函数的经验,我们将如何来研究正、余弦函数呢?
新知讲解
正弦函数、余弦函数的图像
研究正、余弦函数的方法和步骤:
从定义出发研究这个函数,类比已有的研究方法,先画出函数图象,通过观察图象的特征。
由公式sin(x±2π)=sinx,cos(x±2π)=cosx及三角函数线可知:正、余弦函数自变量每增加 (减少)2π,正弦函数值、 余弦函数值将重复出现.
另外,从三角函数线可以看出,正余弦函数在0~2π旋转一周,
然后依次重复,因此,我们可以做出0~2π上的函数图像,进行研
究,然后推广开来即可。
新知讲解
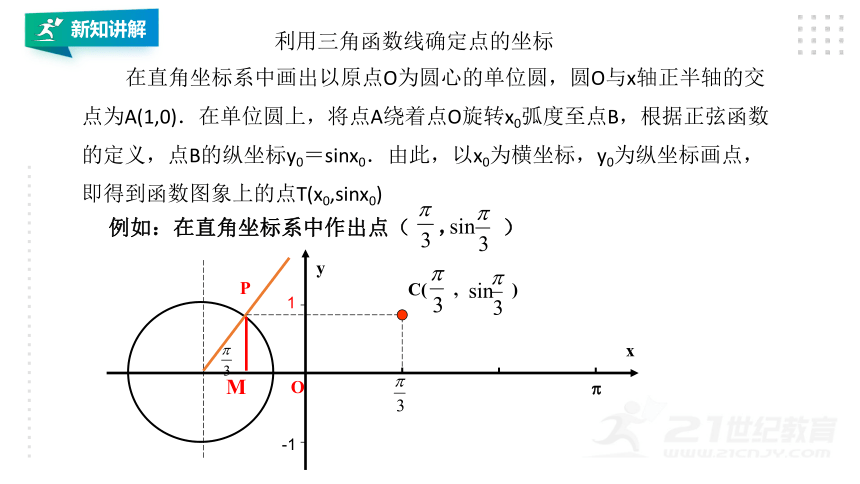
利用三角函数线确定点的坐标
在直角坐标系中画出以原点O为圆心的单位圆,圆O与x轴正半轴的交点为A(1,0).在单位圆上,将点A绕着点O旋转x0弧度至点B,根据正弦函数的定义,点B的纵坐标y0=sinx0.由此,以x0为横坐标,y0为纵坐标画点,即得到函数图象上的点T(x0,sinx0)
例如:在直角坐标系中作出点( , )
P
M
C( , )
y
x
O
1
-1
新知讲解
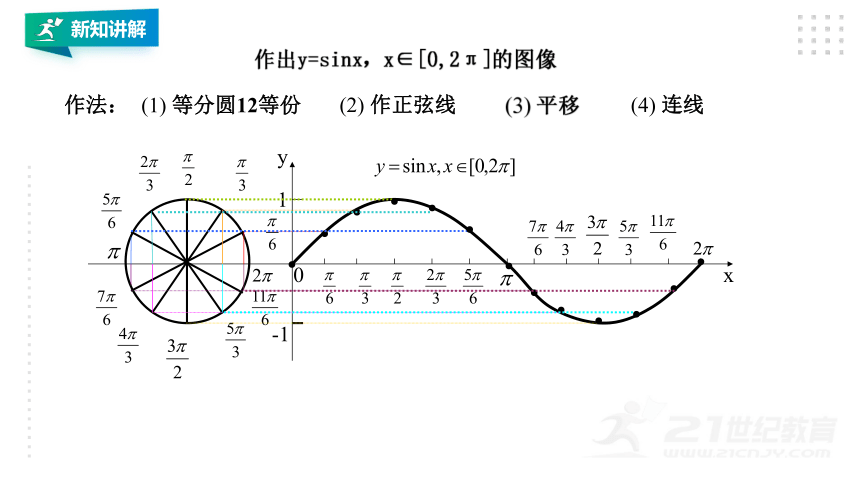
作出y=sinx,x∈[0,2π]的图像
(1) 等分圆12等份
(2) 作正弦线
(3) 平移
(4) 连线
作法:
1
-1
0
y
x
●
●
●
●
●
●
●
●
●
●
●
●
●
新知讲解
利用诱导公式一得到y=sinx,x∈R的图像
π
4
-
o
-
π
2
-
π
3
-
π
2
π
3
π
4
x
y
1
-1
y=sinx,x [0,2 ]
y=sinx,
利用图象平移
x R
sin(x+2kπ)=sinx
如何快速作出y=sinx,x∈[0,2π]的图像
说明:y=sinx,x∈R的图像是一条以y=1为上界,以y=-1为下界的波浪线,
叫做正弦曲线
新知讲解
五点做图法
可以看出图像的五个关键点:一个最高点,三个与x轴交点,一个最低点
-
-1
1
-
-1
五点作图法步骤:
(1)列表(列出关键五点)
(2)描点(描出五个关键点)
(3)连线(用光滑曲线顺次连五个点)
说明:五个关键点分别是:
(0,0)
( , 1)
( ,0)
( ,-1)
( 2 ,0)
新知讲解
例:用五点法作y=sinx , x∈[0, 2π ]的简图
x
0
0 1 0 -1 0
1、列表:
2、描点:
3、连线:
1
x
y
O
-1
新知讲解
余弦函数 y=cosx (x∈R) 的图象
利用诱导公式,以正弦函数的图像为基础,通过适当的图形变换得到余
弦函数的图像.
由诱导公式:
要得到余弦函数图像,只要将正弦函数图像向左平衡 个单位即可。
正弦曲线
x
o
1
-1
-2
-
2
3
4
余弦曲线
在精度要求不高的情况下,余弦曲线也可以利用五点法做出[0,2π]的图像。
例1、画出下列函数的简图:
(1)y=1+sinx,x [0, 2 ]
(2)y=-cosx , x∈[0,2π]
解:(1)由题意列表如下:
x
sinx
Sinx+1
0
1
0
-1
0
1 2 1 0 1
0
2
y=sinx,x [0, 2 ]
y=sinx+1,x [0, 2 ]
y
x
-1
2
1
0
描点
连线
向上平移1个单位
合作探究
解:(2)由题意列表如下:
0
1
-cosx
-1
0
0
1
-1
0
-1
1
描点
连线
-1
1
x
y
●
●
●
●
●
合作探究
课堂练习
1、画出y=1-cosx , x∈[0,2π]的简图
解:(1)列表:
(2)描点
(3)连线
-1
1
x
y
●
●
●
●
●
O
2
y=1-cosx , x∈[0,2π]
课堂总结
2、“五点作图法”
1、几何法作正弦函数的图象
正弦五点:
余弦五点:
3、作函数图象:
五点法
图象变换法
板书设计
1、正弦函数、余弦函数的定义:
正弦函数:y=sinx
余弦函数:y=cosx
2、正、余弦函数图像
正弦曲线
x
o
1
-1
-2
-
2
3
4
余弦曲线
3、五点做图法:
正弦五点:
余弦五点:
作业布置
2.求方程 的实数根的个数。
3.课本P2001、2
https://www.21cnjy.com/help/help_extract.php
5.4.1正、余弦函数图像
人教A(2019)版
九年级上册
新知导入
复习巩固
一、三角函数的单位圆定义:
设 α 是一个任意角,它的终边与单位圆交于点P(x,y)
0
1
1
P(x,y)
M
如图:
sinα=y
cosα=x
α
二、诱导公式:
k∈Z
记忆口诀:奇变偶不变,符号看象限。
三、三角函数线
新知导入
M
P
O
y
x
A(1,0)
T
α
设 α 是一个任意角,它的终边与单位圆交于点P(x,y)
由三角函数定义:
有向线段 、 、 ,叫做三角函
数线,方向与坐标轴方向相同为正,与坐标轴
方向相反为负。
新知讲解
正弦函数、余弦函数的概念
任意给定一个实数x,有唯一确定的值sinx(或cosx)与之对应,
即:f:x→y=sinx(或f:x→y=cosx)
则由上述对应法则确定的函数叫正弦函数(或余弦函数)
正弦函数:y=sinx
余弦函数:y=cosx
由前面的知识我们知道,自变量x∈R,由以往研究函数的经验,我们将如何来研究正、余弦函数呢?
新知讲解
正弦函数、余弦函数的图像
研究正、余弦函数的方法和步骤:
从定义出发研究这个函数,类比已有的研究方法,先画出函数图象,通过观察图象的特征。
由公式sin(x±2π)=sinx,cos(x±2π)=cosx及三角函数线可知:正、余弦函数自变量每增加 (减少)2π,正弦函数值、 余弦函数值将重复出现.
另外,从三角函数线可以看出,正余弦函数在0~2π旋转一周,
然后依次重复,因此,我们可以做出0~2π上的函数图像,进行研
究,然后推广开来即可。
新知讲解
利用三角函数线确定点的坐标
在直角坐标系中画出以原点O为圆心的单位圆,圆O与x轴正半轴的交点为A(1,0).在单位圆上,将点A绕着点O旋转x0弧度至点B,根据正弦函数的定义,点B的纵坐标y0=sinx0.由此,以x0为横坐标,y0为纵坐标画点,即得到函数图象上的点T(x0,sinx0)
例如:在直角坐标系中作出点( , )
P
M
C( , )
y
x
O
1
-1
新知讲解
作出y=sinx,x∈[0,2π]的图像
(1) 等分圆12等份
(2) 作正弦线
(3) 平移
(4) 连线
作法:
1
-1
0
y
x
●
●
●
●
●
●
●
●
●
●
●
●
●
新知讲解
利用诱导公式一得到y=sinx,x∈R的图像
π
4
-
o
-
π
2
-
π
3
-
π
2
π
3
π
4
x
y
1
-1
y=sinx,x [0,2 ]
y=sinx,
利用图象平移
x R
sin(x+2kπ)=sinx
如何快速作出y=sinx,x∈[0,2π]的图像
说明:y=sinx,x∈R的图像是一条以y=1为上界,以y=-1为下界的波浪线,
叫做正弦曲线
新知讲解
五点做图法
可以看出图像的五个关键点:一个最高点,三个与x轴交点,一个最低点
-
-1
1
-
-1
五点作图法步骤:
(1)列表(列出关键五点)
(2)描点(描出五个关键点)
(3)连线(用光滑曲线顺次连五个点)
说明:五个关键点分别是:
(0,0)
( , 1)
( ,0)
( ,-1)
( 2 ,0)
新知讲解
例:用五点法作y=sinx , x∈[0, 2π ]的简图
x
0
0 1 0 -1 0
1、列表:
2、描点:
3、连线:
1
x
y
O
-1
新知讲解
余弦函数 y=cosx (x∈R) 的图象
利用诱导公式,以正弦函数的图像为基础,通过适当的图形变换得到余
弦函数的图像.
由诱导公式:
要得到余弦函数图像,只要将正弦函数图像向左平衡 个单位即可。
正弦曲线
x
o
1
-1
-2
-
2
3
4
余弦曲线
在精度要求不高的情况下,余弦曲线也可以利用五点法做出[0,2π]的图像。
例1、画出下列函数的简图:
(1)y=1+sinx,x [0, 2 ]
(2)y=-cosx , x∈[0,2π]
解:(1)由题意列表如下:
x
sinx
Sinx+1
0
1
0
-1
0
1 2 1 0 1
0
2
y=sinx,x [0, 2 ]
y=sinx+1,x [0, 2 ]
y
x
-1
2
1
0
描点
连线
向上平移1个单位
合作探究
解:(2)由题意列表如下:
0
1
-cosx
-1
0
0
1
-1
0
-1
1
描点
连线
-1
1
x
y
●
●
●
●
●
合作探究
课堂练习
1、画出y=1-cosx , x∈[0,2π]的简图
解:(1)列表:
(2)描点
(3)连线
-1
1
x
y
●
●
●
●
●
O
2
y=1-cosx , x∈[0,2π]
课堂总结
2、“五点作图法”
1、几何法作正弦函数的图象
正弦五点:
余弦五点:
3、作函数图象:
五点法
图象变换法
板书设计
1、正弦函数、余弦函数的定义:
正弦函数:y=sinx
余弦函数:y=cosx
2、正、余弦函数图像
正弦曲线
x
o
1
-1
-2
-
2
3
4
余弦曲线
3、五点做图法:
正弦五点:
余弦五点:
作业布置
2.求方程 的实数根的个数。
3.课本P2001、2
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
