人教版数学七年级下册 第六章《实数》复习 课件(共42张ppt)
文档属性
| 名称 | 人教版数学七年级下册 第六章《实数》复习 课件(共42张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 09:01:17 | ||
图片预览









文档简介
(共42张PPT)
1.知道平方根、立方根的概念,会进行开平方和开立方运算,会求一个非负数的平方根、算术平方根;
2.知道实数的分类;会对实数准确分类;
3.知道实数的有关概念,会进行实数大小比较;
4.能够运用实数的有关知识解决问题。
【学习目标】
正数 的正的平方根也叫做 的算术平方根,
数 的立方根用符号 表示。
一般地,如果 ,那么 叫 的立方根
求一个数的平方根(立方根)的运算,叫做开平方(开立方) 。
一般地,如果一个数的平方等于 ,这个数叫做 的平方根。(也叫二次方根)
平方根、算术平方根、立方根的定义
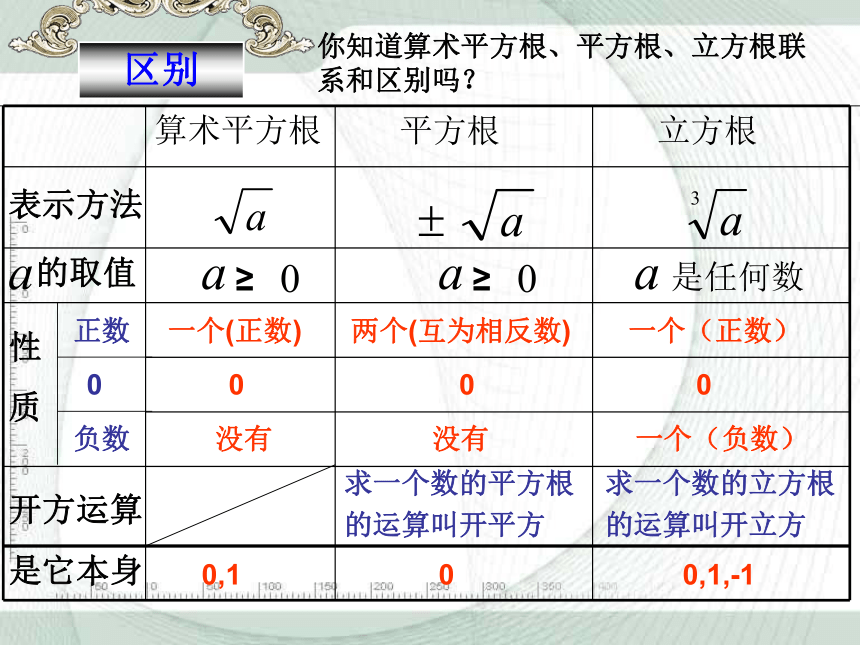
区别
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥
≥
正数
0
负数
一个(正数)
0
没有
两个(互为相反数)
0
没有
一个(正数)
0
一个(负数)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是它本身
0,1
0
0,1,-1
开方运算
1.填一填
25的平方根是 ;16的算术平方根是 ;
27的立方根是 ; 的平方根是 ,
4
3
针对练习一——平方根 立方根
8
-0.4
0.3
±5
±2
针对练习一——平方根 立方根
2.火眼晴晴选一选
(1)下列说法中正确的是( ) A. 的平方根是±3 B.1的立方根是±1
C. =±1 D. 是5的平方根的相反数
(2)下列式子中
① 4是16的算术平方根,即
②4是16的算术平方根,即
③-7是49的算术平方根,即
④7是(-7) 的算术平方根,即
其中正确的是( )
A. ①③ B. ②③ C. ②④ D. ①④
A
C
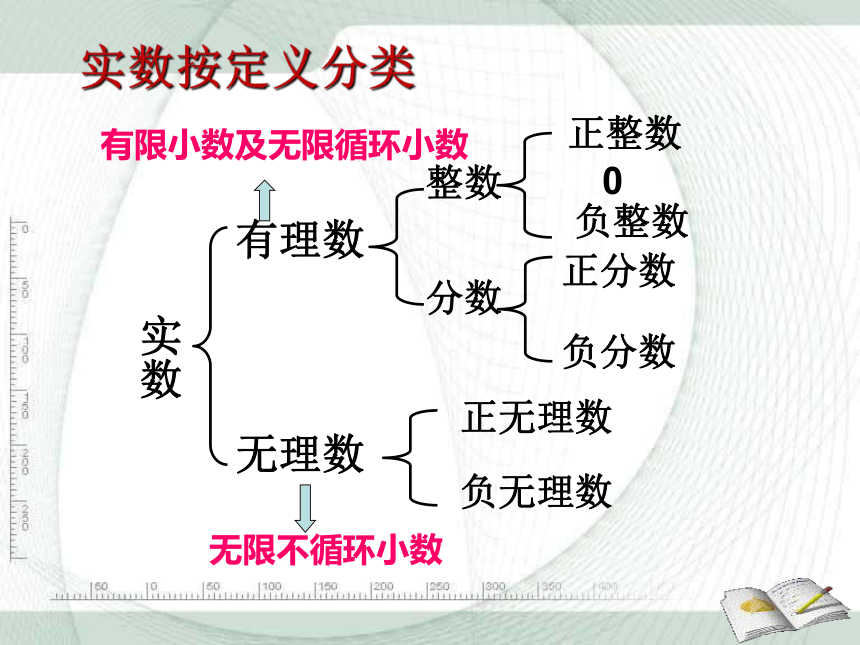
实数
有理数
无理数
正整数
0
负整数
正分数
负分数
分数
整数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
实数按定义分类
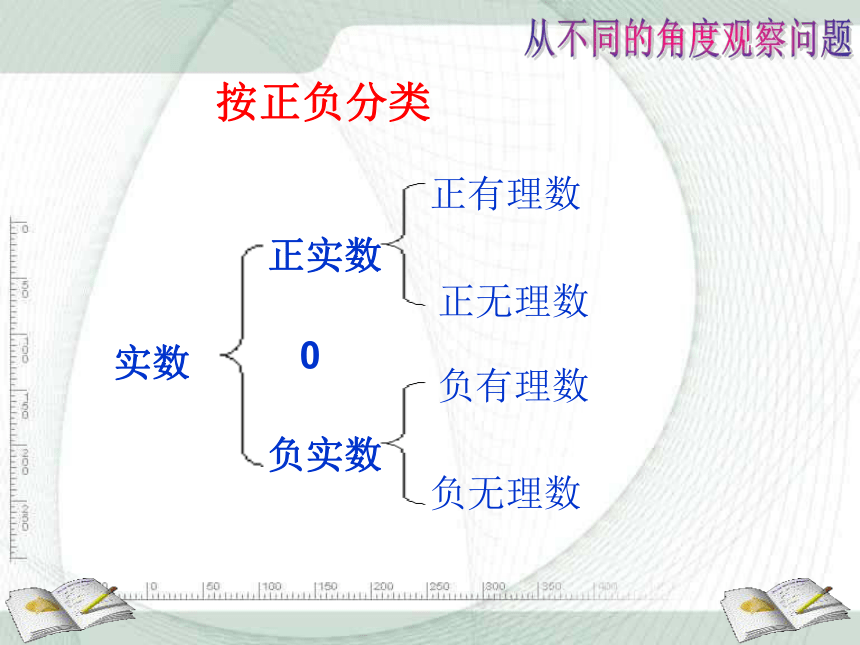
按正负分类
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
针对练习二——实数分类
中无理数的个
A. 2 B. 3 C. 4 D. 5
B
1、在下列各数
数是( )个
2. 下列说法错误的有( )个
①无限小数一定是无理数;
②无理数一定是无限小数;
③带根号的数一定是无理数;
④不带根号的数一定是有理数.
A. 1 B.2 C.3 D.4
C
针对练习二——实数分类
无理数集合:
有理数集合:
整数集合:
分数集合:
3.将下列各数分别填入下列的集合括号中
针对练习二——实数分类
1.实数与数轴:实数与数轴上的点__________对应。
2.实数的相反数、绝对值:
相反数:实数 的相反数为______;
绝对值:正数的绝对值是它的本身;负数的绝对值是它的相反数;零的绝对值是零.即实数的绝对值是非负数。
实数的相关概念及运算
实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且有理数的运算法则与运算律对实数仍然适用。
0
一一
的相反数是 ; 相反数是 ;
; 。
2.
3.如图,以数轴的单位长线段为边做一个正方形,以数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是( ) A.1.5 B.1.4
C. D.
C
针对练习三——实数相关概念、运算
-3
1
0
针对练习三——实数相关概念、运算
4.
5.计算
6.求 的值:
方法:(1)利用数轴:在数轴上表示的两个
实数, 。
正数 零 负数。
(2)利用绝对值:
两个负数比较, 。
(四)实数大小比较
大于
大于
绝对值大的反而小
右边的数总比左边的数大
2.实数 在数轴上的对应点如图所示,
则它们从小到大的顺序是 。
c d 0 b
针对练习四——实数大小比较
1.下列各数中,最小的数是 ( )
A.-1 B.0 C.1 D.-
D
3.比较下列各组数的大小
三、合作探究
2. 如果一个正数的平方根为 和 ,
求这个正数。
通过这节课的学习,你有何收获
本节课你有什么收获,还有什么疑问?
我要说……
(1)实数 (相相邻两个1之间依次多一个0),其中无理数是( )个。
A.1 B.2 C.3 D.4
(2)实数 在数轴上的位置如图4所示,则 ( )
A. B.
C. D.
(3) 估计的值在( )之间。
A.1与2之间 B.2与3之间
C.3与4之间 D.4与5之间
四、当堂检测
B
B
B
1.选择题
(1) 这四个数中,最大的是 。
(2) 的平方根是 。
(3)若实数 、b满足 ,则 = 。
2.填空题
±3
1
4
-6
81
-2
(4)
拓展延伸
1.
17.38
2
0.236
2.
3.
4.
练习:1、—8是 的平方根, 64的平方根是 ;
的平方根是 。
2、 的立方根是( ), 的平方根是 ( )
3.当x ______ 时,2x-1没有平方根
5.一个正数x的两个平方根分别是a+1和a-3,则
a= ,x=
<0.5
X=7
1
4
64
±8
8
-4
3
2
-64的立方根是_____
=
几个基本公式:(注意字母
的取值范围)
=
-
练习:
1、判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
7.平面直角坐标系中的点与有序实数对之间是
一一对应的。( )
√
2.把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
1. x取何值时,下列各式有意义
三、知识巩固
解(1)x≤4
(2) X为任何实数
不要遗漏
2.解方程:
当方程中出现平方时,若有解,一般都有两个解
当方程中出现立方时,一般都有一个解
(1).
解:
(2).
解:
1.已知 和 的和为0,则x的范围是为( )
A.任意实数 B.非正实数 C .非负实数 D. 0
2.若- = ,则m的值是 ( )
A B C D
3. 若 成立,则x的取值范围是( )
A.x≤2 B. x≥2 C. 0 ≤x ≤ 2 D.任意实数
4.若 =4-x成立,则x的取值范围是( )
A.x≤4 B. x≥4 C. 0 ≤x ≤ 4 D.任意实数
B
B
A
D
3、若
,则
x的取值范围是 ___
4、已知
位置如图所示,
试化简
x≤2
解:原式=-a-(b-a)+(c-a)-(c-b)
=-a-b+a+c-a-c+b=-a
解:原式=-(a+b-c)+(-b+2c)+(b-a)
=-a-b+c-b+2c+b-a=-2a-b+3c
5、已知
的小数部分为m,
,
的小数部分为n
6、计算:
1
解:原式=1.2+0.4+1-2
=0.6
解:原式=3+5-1+4
=11
五、强化运用
1、下列说法正确的是( )
A、
B 表示6的算术平方根的相反数
C、 任何数都有平方根 D、
一定没有平方根
B
-5
x≤0
X为任何实数
5、已知等腰三角形的两边长
满足
,求三角形的周长
解:由题意得:
2x-1≥0
1-2x≥0
{
{
解得:
,y=1
∴2x+3y=4
解:由题意,得
2a-3b+5=0
2a-3b-13=0
{
{
解得:
a=2
b=3
所以等腰三角形的三边为2,2,3或2,3,3
所以,三角形的周长为7或8
6、已知
,求
的值。
7、已知
,求 y-x的算术
平方根
解:由题意得:
{
{
a-4≥0
解得a≥4
∴ a-3+
∴a-4=9
∴a=13
解:由题意,得:
X-2≥0
2-x≥0
解得:
x≥2
x≤2
∴x=2
当x=2时,y=3
解:由题意,得
解:由题意,得:
{
{
{
{
X-2y-3=0
2x-3y-5=0
解得
x=1
y=-1
x=8
y-1=0
z-3=0
解得:
x=8
y=1
z=3
11、若
为实数,则下列命题正确的是( )
B、
C、
D、
A、
12. 若 成立,则x的取值范围是( )
A.x≤2 B. x≥2 C. 0 ≤x ≤ 2 D.任意实数
13 .若 =4-x成立,则x的取值范围是( )
A.x≤4 B. x≥4 C. 0 ≤x ≤ 4 D.任意实数
A
D
D
选择题
A.0 B. C.0 D.不存在
A.原点左侧 B.原点右侧 C.原点或原点左侧 D.原点或原点右侧
A.0个 B.1 个 C.2个 D.3个
A.2或12 B.2或-12 C.-2或12 D.-2或-12
1.如果一个数的平方根为a+1和2a-7, 求这个数
3.已知y= 求2(x+y)的平方根
4.已知5+ 的小数部分为 m, 7- 的小数部分为n,求m+n的值
5.已知满足 ,求a的值
2.已知等腰三角形两边长a,b满足
求此等腰三角形的周长
1、 的平方根是_ _ _ _ _ ,3-2的算术平方根是_ _ _ _ _ ,立方根为其本身的实数_ _ _ _ _。
2、已知 ,则实数 的相反数是 。
3计算:(1)23+ +(6-π)0- .
(2)
1.知道平方根、立方根的概念,会进行开平方和开立方运算,会求一个非负数的平方根、算术平方根;
2.知道实数的分类;会对实数准确分类;
3.知道实数的有关概念,会进行实数大小比较;
4.能够运用实数的有关知识解决问题。
【学习目标】
正数 的正的平方根也叫做 的算术平方根,
数 的立方根用符号 表示。
一般地,如果 ,那么 叫 的立方根
求一个数的平方根(立方根)的运算,叫做开平方(开立方) 。
一般地,如果一个数的平方等于 ,这个数叫做 的平方根。(也叫二次方根)
平方根、算术平方根、立方根的定义
区别
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥
≥
正数
0
负数
一个(正数)
0
没有
两个(互为相反数)
0
没有
一个(正数)
0
一个(负数)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
是它本身
0,1
0
0,1,-1
开方运算
1.填一填
25的平方根是 ;16的算术平方根是 ;
27的立方根是 ; 的平方根是 ,
4
3
针对练习一——平方根 立方根
8
-0.4
0.3
±5
±2
针对练习一——平方根 立方根
2.火眼晴晴选一选
(1)下列说法中正确的是( ) A. 的平方根是±3 B.1的立方根是±1
C. =±1 D. 是5的平方根的相反数
(2)下列式子中
① 4是16的算术平方根,即
②4是16的算术平方根,即
③-7是49的算术平方根,即
④7是(-7) 的算术平方根,即
其中正确的是( )
A. ①③ B. ②③ C. ②④ D. ①④
A
C
实数
有理数
无理数
正整数
0
负整数
正分数
负分数
分数
整数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
实数按定义分类
按正负分类
实数
正实数
负实数
0
正有理数
正无理数
负有理数
负无理数
针对练习二——实数分类
中无理数的个
A. 2 B. 3 C. 4 D. 5
B
1、在下列各数
数是( )个
2. 下列说法错误的有( )个
①无限小数一定是无理数;
②无理数一定是无限小数;
③带根号的数一定是无理数;
④不带根号的数一定是有理数.
A. 1 B.2 C.3 D.4
C
针对练习二——实数分类
无理数集合:
有理数集合:
整数集合:
分数集合:
3.将下列各数分别填入下列的集合括号中
针对练习二——实数分类
1.实数与数轴:实数与数轴上的点__________对应。
2.实数的相反数、绝对值:
相反数:实数 的相反数为______;
绝对值:正数的绝对值是它的本身;负数的绝对值是它的相反数;零的绝对值是零.即实数的绝对值是非负数。
实数的相关概念及运算
实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且有理数的运算法则与运算律对实数仍然适用。
0
一一
的相反数是 ; 相反数是 ;
; 。
2.
3.如图,以数轴的单位长线段为边做一个正方形,以数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是( ) A.1.5 B.1.4
C. D.
C
针对练习三——实数相关概念、运算
-3
1
0
针对练习三——实数相关概念、运算
4.
5.计算
6.求 的值:
方法:(1)利用数轴:在数轴上表示的两个
实数, 。
正数 零 负数。
(2)利用绝对值:
两个负数比较, 。
(四)实数大小比较
大于
大于
绝对值大的反而小
右边的数总比左边的数大
2.实数 在数轴上的对应点如图所示,
则它们从小到大的顺序是 。
c d 0 b
针对练习四——实数大小比较
1.下列各数中,最小的数是 ( )
A.-1 B.0 C.1 D.-
D
3.比较下列各组数的大小
三、合作探究
2. 如果一个正数的平方根为 和 ,
求这个正数。
通过这节课的学习,你有何收获
本节课你有什么收获,还有什么疑问?
我要说……
(1)实数 (相相邻两个1之间依次多一个0),其中无理数是( )个。
A.1 B.2 C.3 D.4
(2)实数 在数轴上的位置如图4所示,则 ( )
A. B.
C. D.
(3) 估计的值在( )之间。
A.1与2之间 B.2与3之间
C.3与4之间 D.4与5之间
四、当堂检测
B
B
B
1.选择题
(1) 这四个数中,最大的是 。
(2) 的平方根是 。
(3)若实数 、b满足 ,则 = 。
2.填空题
±3
1
4
-6
81
-2
(4)
拓展延伸
1.
17.38
2
0.236
2.
3.
4.
练习:1、—8是 的平方根, 64的平方根是 ;
的平方根是 。
2、 的立方根是( ), 的平方根是 ( )
3.当x ______ 时,2x-1没有平方根
5.一个正数x的两个平方根分别是a+1和a-3,则
a= ,x=
<0.5
X=7
1
4
64
±8
8
-4
3
2
-64的立方根是_____
=
几个基本公式:(注意字母
的取值范围)
=
-
练习:
1、判断下列说法是否正确:
1.实数不是有理数就是无理数。 ( )
2.无限小数都是无理数。 ( )
3.无理数都是无限小数。 ( )
4.带根号的数都是无理数。 ( )
5.两个无理数之和一定是无理数。( )
6.所有的有理数都可以在数轴上表示,反过来,数轴上所有的点都表示有理数。( )
7.平面直角坐标系中的点与有序实数对之间是
一一对应的。( )
√
2.把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
1. x取何值时,下列各式有意义
三、知识巩固
解(1)x≤4
(2) X为任何实数
不要遗漏
2.解方程:
当方程中出现平方时,若有解,一般都有两个解
当方程中出现立方时,一般都有一个解
(1).
解:
(2).
解:
1.已知 和 的和为0,则x的范围是为( )
A.任意实数 B.非正实数 C .非负实数 D. 0
2.若- = ,则m的值是 ( )
A B C D
3. 若 成立,则x的取值范围是( )
A.x≤2 B. x≥2 C. 0 ≤x ≤ 2 D.任意实数
4.若 =4-x成立,则x的取值范围是( )
A.x≤4 B. x≥4 C. 0 ≤x ≤ 4 D.任意实数
B
B
A
D
3、若
,则
x的取值范围是 ___
4、已知
位置如图所示,
试化简
x≤2
解:原式=-a-(b-a)+(c-a)-(c-b)
=-a-b+a+c-a-c+b=-a
解:原式=-(a+b-c)+(-b+2c)+(b-a)
=-a-b+c-b+2c+b-a=-2a-b+3c
5、已知
的小数部分为m,
,
的小数部分为n
6、计算:
1
解:原式=1.2+0.4+1-2
=0.6
解:原式=3+5-1+4
=11
五、强化运用
1、下列说法正确的是( )
A、
B 表示6的算术平方根的相反数
C、 任何数都有平方根 D、
一定没有平方根
B
-5
x≤0
X为任何实数
5、已知等腰三角形的两边长
满足
,求三角形的周长
解:由题意得:
2x-1≥0
1-2x≥0
{
{
解得:
,y=1
∴2x+3y=4
解:由题意,得
2a-3b+5=0
2a-3b-13=0
{
{
解得:
a=2
b=3
所以等腰三角形的三边为2,2,3或2,3,3
所以,三角形的周长为7或8
6、已知
,求
的值。
7、已知
,求 y-x的算术
平方根
解:由题意得:
{
{
a-4≥0
解得a≥4
∴ a-3+
∴a-4=9
∴a=13
解:由题意,得:
X-2≥0
2-x≥0
解得:
x≥2
x≤2
∴x=2
当x=2时,y=3
解:由题意,得
解:由题意,得:
{
{
{
{
X-2y-3=0
2x-3y-5=0
解得
x=1
y=-1
x=8
y-1=0
z-3=0
解得:
x=8
y=1
z=3
11、若
为实数,则下列命题正确的是( )
B、
C、
D、
A、
12. 若 成立,则x的取值范围是( )
A.x≤2 B. x≥2 C. 0 ≤x ≤ 2 D.任意实数
13 .若 =4-x成立,则x的取值范围是( )
A.x≤4 B. x≥4 C. 0 ≤x ≤ 4 D.任意实数
A
D
D
选择题
A.0 B. C.0 D.不存在
A.原点左侧 B.原点右侧 C.原点或原点左侧 D.原点或原点右侧
A.0个 B.1 个 C.2个 D.3个
A.2或12 B.2或-12 C.-2或12 D.-2或-12
1.如果一个数的平方根为a+1和2a-7, 求这个数
3.已知y= 求2(x+y)的平方根
4.已知5+ 的小数部分为 m, 7- 的小数部分为n,求m+n的值
5.已知满足 ,求a的值
2.已知等腰三角形两边长a,b满足
求此等腰三角形的周长
1、 的平方根是_ _ _ _ _ ,3-2的算术平方根是_ _ _ _ _ ,立方根为其本身的实数_ _ _ _ _。
2、已知 ,则实数 的相反数是 。
3计算:(1)23+ +(6-π)0- .
(2)
