沪科版数学八年级上册 14.1 全等三角形 课件(共15张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 14.1 全等三角形 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 817.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 09:07:19 | ||
图片预览



文档简介
(共15张PPT)
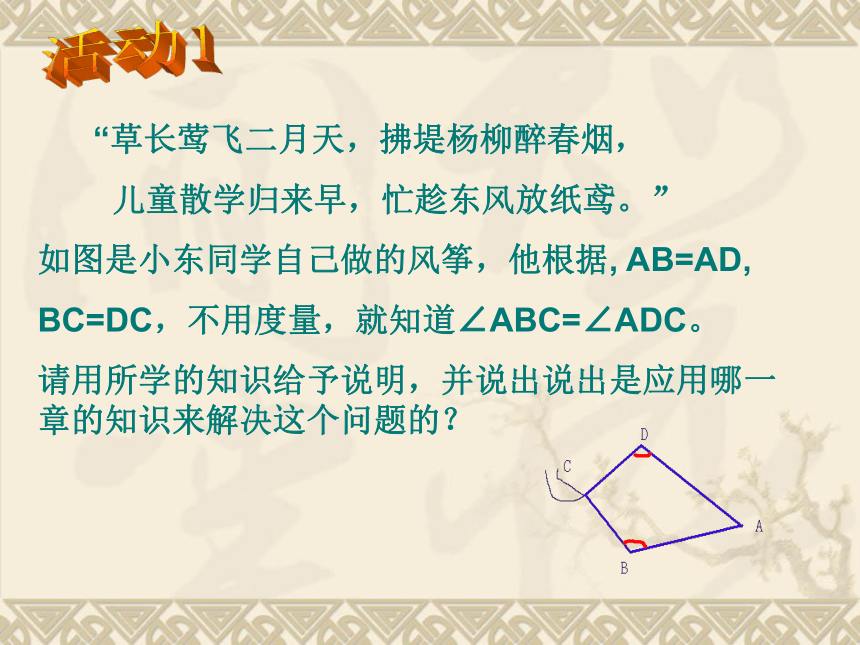
“草长莺飞二月天,拂堤杨柳醉春烟,
儿童散学归来早,忙趁东风放纸鸢。”
如图是小东同学自己做的风筝,他根据, AB=AD,
BC=DC,不用度量,就知道∠ABC=∠ADC。
请用所学的知识给予说明,并说出说出是应用哪一章的知识来解决这个问题的?
全等三角形的性质:
全等三角形的对应边、对应角相等.
全等三角形的判定
知识点回顾(一)
一般三角形全等的判定:
SSS、SAS、 ASA、AAS
直角三角形全等的判定:
SSS、SAS、 ASA、AAS 、HL
全等图形的定义:
能完全重合的图形叫全等图形
全等三角形的定义:
能完全重合的三角形是
全等三角形.
(1)三个角对应相等两个三角形一定全等吗
(2)一般的两个三角形中如果有两条边和其中
一条边的对角对应相等的这两个三角形
一定全等吗
三个角对应相等的两个三角形不一定全等
三个角对应相等的两个三角形全等吗?
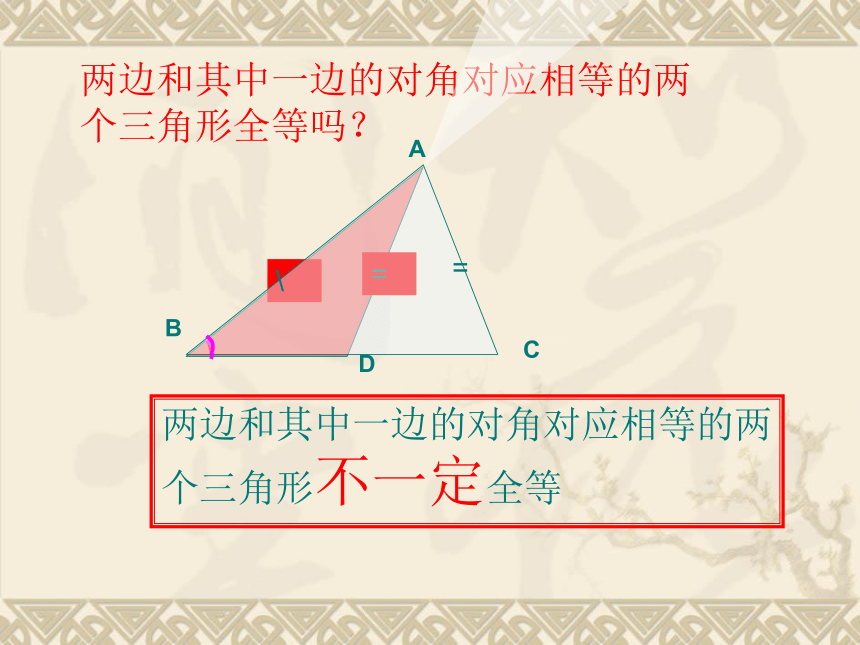
两边和其中一边的对角对应相等的两个三角形不一定全等
两边和其中一边的对角对应相等的两个三角形全等吗?
\
=
\
=
A
B
D
C
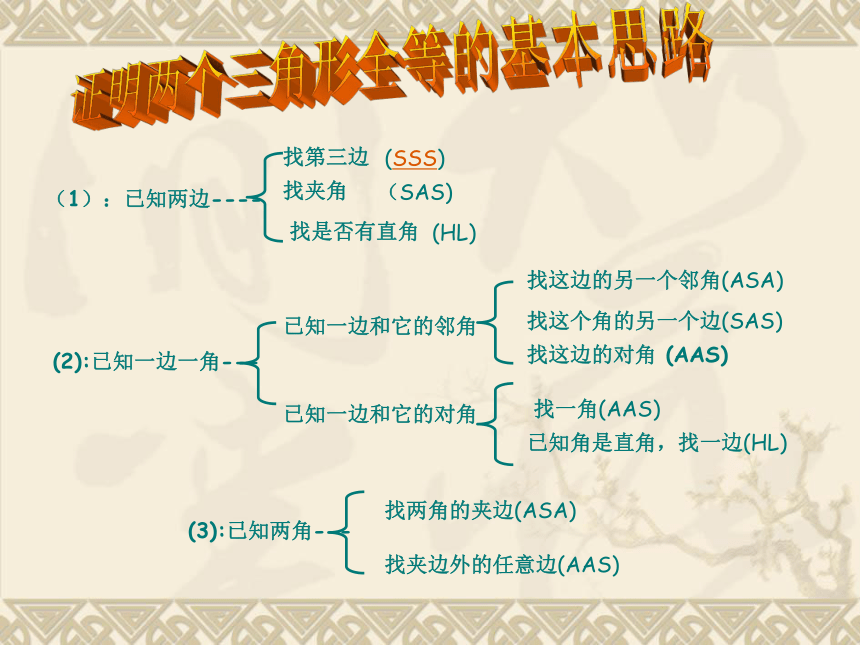
(1):已知两边----
找第三边
(SSS)
找夹角
(SAS)
(2):已知一边一角---
已知一边和它的邻角
找是否有直角
(HL)
已知一边和它的对角
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS)
找这边的对角 (AAS)
找一角(AAS)
已知角是直角,找一边(HL)
(3):已知两角---
找两角的夹边(ASA)
找夹边外的任意边(AAS)
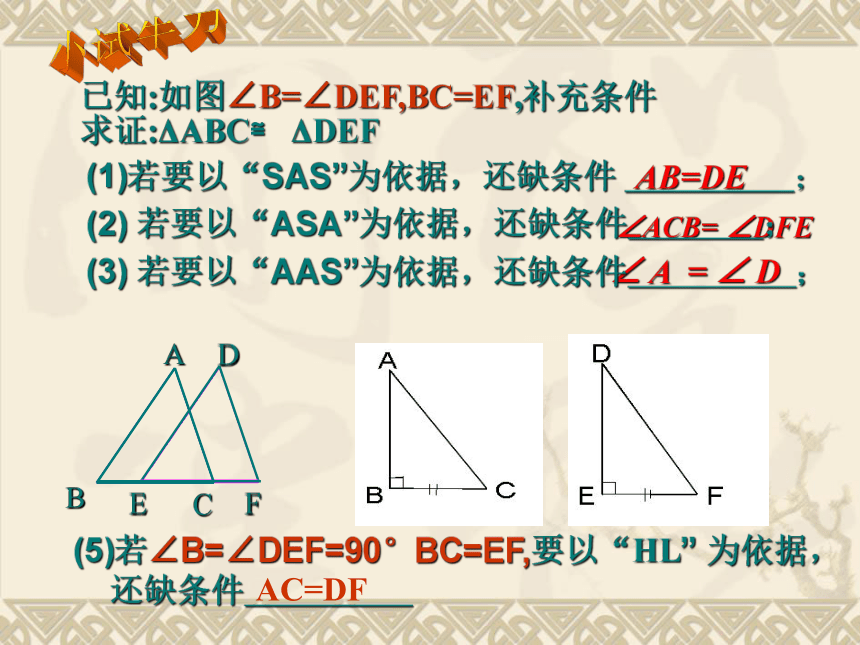
已知:如图∠B=∠DEF,BC=EF,补充条件
求证:ΔABC≌ ΔDEF
∠ACB= ∠DFE
AB=DE
A
B
C
D
E
F
=
=
D
E
F
A
B
C
∠ A = ∠ D
(1)若要以“SAS”为依据,还缺条件 _____;
(2) 若要以“ASA”为依据,还缺条件____;
(3) 若要以“AAS”为依据,还缺条件_____;
(5)若∠B=∠DEF=90°BC=EF,要以“HL” 为依据,
还缺条件_____
AC=DF
一、挖掘“隐含条件”判全等
1.如图(1),AB=DC,AC=DB,则△ABC≌△DCB吗 说说理由
A
D
B
C
图(1)
2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C= ,BE= .说说理由.
B
C
O
D
E
A
图(2)
3.如图(3),AC与BD相交于o,若OB=OD,∠A=∠C,若AB=3cm,则CD= . 说说理由.
A
D
B
C
O
图(3)
20°
5cm
3cm
友情提示:公共边,公共角,
对顶角这些都是隐含的边,角相等的条件!
二、熟练转化“间接条件”判全等
4.如图,AE=CF,∠AFD=∠CEB,DF=BE;△AFD与△ CEB全等吗?为什么?
A
D
B
C
F
E
解: △AFD与△ CEB全等,理由是:
∵ AE=CF
∴ AE-EF=CF-EF
∴ AF=CE
在△AFD与△ CEB中
AF=CE
∠AFD=∠CEB
DF=BE
∴ △AFD≌△ CEB(SAS)
解: BC=DE,理由是:
∵ ∠CAE=∠BAD
∴ ∠CAE+ ∠ EAB ∠ =∠BAD + ∠EAB
∴ ∠CAB= ∠EAD
在△ CAB与△ EAD中
∠CAB= ∠EAD
∠B=∠D
AC=AE
∴ △ CAB ≌ △ EAD(AAS)
∴ED=CB
5.如图在△ ABC、 △ ADE中∠B=∠D,
AC=AE, 且∠CAE=∠BAD,
则BC=DE 吗?为什么?
A
C
E
B
D
等量加等量和相等,等量减等量差相等,都是用来间接
找边和角相等的方法!
已知,如图,AB=AC,DB=DC,F是AD的延长线上的一点,试说明:BF=CF.
证明:在△ABD和△ACD中
AB=AC
BD=CD
AD=AD
∴ △ABD≌ △ACD(SSS)
∴∠BAD= ∠CAD又∵F是AD延长线上一点,∴∠BAF= ∠CAF
在△ABF和△ACF中
AB=AC
∠BAF= ∠CAF
AF=AF
∴ △ABF≌ △ACF(SAS)∴ BF=CF
∟
∟
C
A
B
E
F
如图,在△ABC中, AC=BC,∠ACB=90°, ∠ CAB的角平分线AE交边CB于E点,过E点作EF⊥AB于F,已知AB等于10㎝,求△EFB的周长?
议一议(有困难和同桌商量一下解决)
EF+EB
FB
解:∵AE平分∠ CAB ,EF⊥AB于F , ∠ACB=90°∴EC ⊥AC于C
∴CE=FE, 又∵AE=AE, ∴Rt △ACE≌ Rt △AFE(HL)
∴AC=AF, ∴EF+BE=CE+BE=BC=AC=AF,
∴EF+BE+BF=AF+BF=AB=10㎝
即△EFB的周长为10㎝。
你有哪些收获呢?
与大家共分享!
学而不思则罔
回头一看,我想说…
请同学们回去后自己找几个你认为与本章有关的题目与同桌进行交流!
课后作业
合作学习‘乐在其中…
知识象一艘船
让它载着我们
驶向理想的
……
谢谢各位老师同学!
“草长莺飞二月天,拂堤杨柳醉春烟,
儿童散学归来早,忙趁东风放纸鸢。”
如图是小东同学自己做的风筝,他根据, AB=AD,
BC=DC,不用度量,就知道∠ABC=∠ADC。
请用所学的知识给予说明,并说出说出是应用哪一章的知识来解决这个问题的?
全等三角形的性质:
全等三角形的对应边、对应角相等.
全等三角形的判定
知识点回顾(一)
一般三角形全等的判定:
SSS、SAS、 ASA、AAS
直角三角形全等的判定:
SSS、SAS、 ASA、AAS 、HL
全等图形的定义:
能完全重合的图形叫全等图形
全等三角形的定义:
能完全重合的三角形是
全等三角形.
(1)三个角对应相等两个三角形一定全等吗
(2)一般的两个三角形中如果有两条边和其中
一条边的对角对应相等的这两个三角形
一定全等吗
三个角对应相等的两个三角形不一定全等
三个角对应相等的两个三角形全等吗?
两边和其中一边的对角对应相等的两个三角形不一定全等
两边和其中一边的对角对应相等的两个三角形全等吗?
\
=
\
=
A
B
D
C
(1):已知两边----
找第三边
(SSS)
找夹角
(SAS)
(2):已知一边一角---
已知一边和它的邻角
找是否有直角
(HL)
已知一边和它的对角
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS)
找这边的对角 (AAS)
找一角(AAS)
已知角是直角,找一边(HL)
(3):已知两角---
找两角的夹边(ASA)
找夹边外的任意边(AAS)
已知:如图∠B=∠DEF,BC=EF,补充条件
求证:ΔABC≌ ΔDEF
∠ACB= ∠DFE
AB=DE
A
B
C
D
E
F
=
=
D
E
F
A
B
C
∠ A = ∠ D
(1)若要以“SAS”为依据,还缺条件 _____;
(2) 若要以“ASA”为依据,还缺条件____;
(3) 若要以“AAS”为依据,还缺条件_____;
(5)若∠B=∠DEF=90°BC=EF,要以“HL” 为依据,
还缺条件_____
AC=DF
一、挖掘“隐含条件”判全等
1.如图(1),AB=DC,AC=DB,则△ABC≌△DCB吗 说说理由
A
D
B
C
图(1)
2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,CD=5cm,则∠C= ,BE= .说说理由.
B
C
O
D
E
A
图(2)
3.如图(3),AC与BD相交于o,若OB=OD,∠A=∠C,若AB=3cm,则CD= . 说说理由.
A
D
B
C
O
图(3)
20°
5cm
3cm
友情提示:公共边,公共角,
对顶角这些都是隐含的边,角相等的条件!
二、熟练转化“间接条件”判全等
4.如图,AE=CF,∠AFD=∠CEB,DF=BE;△AFD与△ CEB全等吗?为什么?
A
D
B
C
F
E
解: △AFD与△ CEB全等,理由是:
∵ AE=CF
∴ AE-EF=CF-EF
∴ AF=CE
在△AFD与△ CEB中
AF=CE
∠AFD=∠CEB
DF=BE
∴ △AFD≌△ CEB(SAS)
解: BC=DE,理由是:
∵ ∠CAE=∠BAD
∴ ∠CAE+ ∠ EAB ∠ =∠BAD + ∠EAB
∴ ∠CAB= ∠EAD
在△ CAB与△ EAD中
∠CAB= ∠EAD
∠B=∠D
AC=AE
∴ △ CAB ≌ △ EAD(AAS)
∴ED=CB
5.如图在△ ABC、 △ ADE中∠B=∠D,
AC=AE, 且∠CAE=∠BAD,
则BC=DE 吗?为什么?
A
C
E
B
D
等量加等量和相等,等量减等量差相等,都是用来间接
找边和角相等的方法!
已知,如图,AB=AC,DB=DC,F是AD的延长线上的一点,试说明:BF=CF.
证明:在△ABD和△ACD中
AB=AC
BD=CD
AD=AD
∴ △ABD≌ △ACD(SSS)
∴∠BAD= ∠CAD又∵F是AD延长线上一点,∴∠BAF= ∠CAF
在△ABF和△ACF中
AB=AC
∠BAF= ∠CAF
AF=AF
∴ △ABF≌ △ACF(SAS)∴ BF=CF
∟
∟
C
A
B
E
F
如图,在△ABC中, AC=BC,∠ACB=90°, ∠ CAB的角平分线AE交边CB于E点,过E点作EF⊥AB于F,已知AB等于10㎝,求△EFB的周长?
议一议(有困难和同桌商量一下解决)
EF+EB
FB
解:∵AE平分∠ CAB ,EF⊥AB于F , ∠ACB=90°∴EC ⊥AC于C
∴CE=FE, 又∵AE=AE, ∴Rt △ACE≌ Rt △AFE(HL)
∴AC=AF, ∴EF+BE=CE+BE=BC=AC=AF,
∴EF+BE+BF=AF+BF=AB=10㎝
即△EFB的周长为10㎝。
你有哪些收获呢?
与大家共分享!
学而不思则罔
回头一看,我想说…
请同学们回去后自己找几个你认为与本章有关的题目与同桌进行交流!
课后作业
合作学习‘乐在其中…
知识象一艘船
让它载着我们
驶向理想的
……
谢谢各位老师同学!
