沪科版数学九年级上册 21.5 反比例函数 课件(共36张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 21.5 反比例函数 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 631.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 09:33:34 | ||
图片预览











文档简介
(共36张PPT)
反比例函数
1.长方形的长为6,宽y和面积x之间有什么关系?
2.长方形的面积为6,一边长x和另一边长y之间有什么关系?
xy=6
写出下列各关系式:
两个相关联的量,一个量变化,另一个量也随着变化。
如果两个变量的积是一个不为零的常数,我们就说这两个变量成反比例。
正比例
反比例
xy=6
1.北京到杭州的铁路线长为1661km。一列火车从北京开往杭州,记火车全程的行驶时间为x(h),火车行驶的平均速度为y(km/h)。
x(h) 12 15 17 22
y(km/h) 87.4
(2)y与x成什么比例关系?能用一个数学解析式表示吗?
138.4
97.7
110.7
75.5
19
成反比例关系
xy=1661
(1)你能完成下列表格吗?
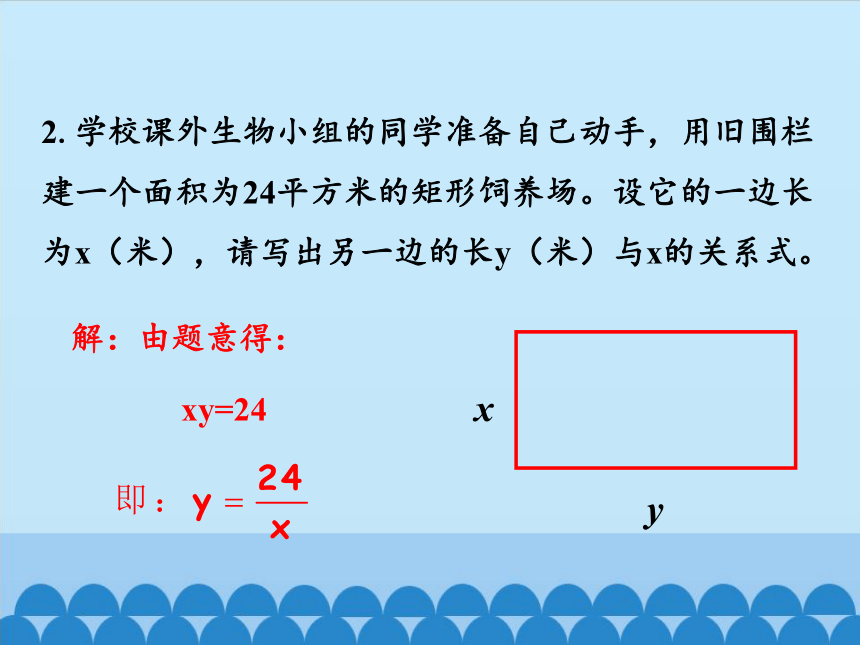
2.学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为24平方米的矩形饲养场。设它的一边长为x(米),请写出另一边的长y(米)与x的关系式。
解:由题意得:
x
y
xy=24
发现
一般地,若变量y与x成反比例,则有xy=k
(k为常数,k≠0),
其中x是自变量,y是x的函数,k叫做比例系数。
形如 (k是常数,k≠0)的函数叫做反比例函数。
巩固练习:
(1)y=-3x
1.下列函数中,哪些y是x的反比例函数?并说出反比例函数的比例系数:
不是反比例函数
不是反比例函数
是反比例函数,比例系数为5。
是反比例函数,比例系数为-6。
是反比例函数,比例系数为 。
不是反比例函数
2.已知反比例函数 。
(1)说出比例系数;
(2)求当x=-10时函数的值;
(3)求当y=2.5时自变量x的值。
解:(1)比例系数是 。
(2)当x=-10时,
(3)当y=2.5时,
3.设面积为10cm的三角形的一边长为a(cm),这条边上的高为h(cm)。
(3)求当边长a=2.5cm时,这条边上的高。
(2)h关于a的函数是不是反比例函数?如果是,请说出它的比例系数。
(1)求h关于a的函数解析式及自变量a的取值范围;
给我一个支点,我可以撬动地球!
——阿基米德
背景知识
阻力×阻力臂=动力×动力臂
阻力臂
阻力
动力臂
动力
背景知识
杠杆定律
(1)求y关于x的函数解析式。这个函数是反比例函数吗?如果是,请说出比例系数。
【例】如图,阻力为1000N,阻力臂长为5cm。设动力为y(N),动力臂为x(cm)。(图中杠杆本身所受重力略去不计。杠杆平衡时,动力×动力臂=阻力×阻力臂)
解:根据题意,得y×x=1000×5
所以所求函数的解析式为
这个函数是反比例函数,比例系数为5000。
(2)求当x=50时函数y的值,并说明这个值的实际意义。
解:当x=50时,
这个函数值的实际意义是,当动力臂长为50cm时,所需动力为100N。
(3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n(n>1)倍时,所需动力将怎样变化?
解:设原来的动力臂长为d(cm),动力为y1(N);扩大后的动力臂长为nd(cm)(n>1),动力为y2(N)。
将x=d,x=nd分别代入
所以当动力臂长扩大到原来的n倍时,所需动力缩小到原来的 。
知者先行:
1.当m为何值时,函数 是反比例函数,并求出其函数解析式。
2.若是函数 是反比例函数,求此反比例函数的关系式。
3.设y=y1+y2,且y1与x成正比例,y2与x成反比例。当x=1时,y=1;当x=2时,y=-1。
(1)求y与x的关系式;(2)求当x=3时,y的值。
归纳
(1)k叫做反比例函数的比例系数;
(2)反比例函数的自变量x的值不能为零。
(3)反比例函数的确定:待定系数法。
(4) 常见的表达形式:xy=k(k≠0)、y=kx-1(k≠0)。
形如 ( k是常数,k≠0 )的函数叫做反比例函数。
1.下列函数中哪些是y关于x的反比例函数?
①y=3x-1;②y=2x-1;③ ④
⑤ ⑥ ⑦ ⑧
2.已知△ABC的面积为12,则△ABC的高h与它的底边a的函数关系式为 。
3.已知y是x的反比例函数,下表给出了x和y的一些值:
x -2 -1 1 3
y 2 -1
(1)求出这个反比例函数的解析式: 。
思考:表中能否增加x=0或y=0的值,为什么?
(2)根据函数解析式完成上表。
1
-2
2
函数图象画法
列
表
描
点
连
线
描点法
反比例函数的图象又会是什么样子呢?
你还记得作函数图象的一般步骤吗?
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来)。
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
y=
x
6
y=
x
6
列
表
描
点
连
线
描点法
注意:一般情况取8个点。
例 画出反比例函数 和 的函数图象。
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
从画反比例函数图象看,描点法还应注意什么?
反比例函数图象画法步骤:
列
表
描
点
连
线
描点法
注意:①列x与y的对应值表时, x的值不能为零,但仍可以零的基础,左右均匀、对称地取值。
至少左右各4个。
注意:②描点时自左往右用光滑曲线顺次连结,切忌用折线。
注意:③两个分支合起来才是反比例函数图象。两个分支不能到达x轴、y轴。
2.反比例函数 的图象在哪两个象限?由什么确定?
3.反比例函数 具有怎样的对称性?
4.反比例函数 的图象的变化趋势是怎样的,它和两条坐标轴的位置关系是怎样的?
1.反比例函数 和 的图象在哪两个象限?它们相同吗?
y=
x
6
x
y
0
y
x
x
6
y=
0
议一议
讨论
1.当k>0时,图象的两个分支分别在第一、三象限内,y随x的增大而减小。
2.当k<0时,图象的两个分支分别在第二、四象限内,y随x的增大而增大。
y=
x
6
x
y
0
y
x
x
6
y=
0
3.图象的两个分支关于直角坐标系的原点成中心对称。
如果知道双曲线的一支,利用对称性,如何画另一支?
4.双曲线无限接近于x、y轴,但永远不会与坐标轴相交。
你能总结一下反比例函数的图象性质特征吗?
图象是双曲线
当k>0时,双曲线分别位于第一、三象限内
当k<0时,双曲线分别位于第二、四象限内
双曲线是中心对称图形
形状
位置
变化趋势
对称性
双曲线无限接近于x、y轴,但永远不会与坐标轴相交
对称中心
坐标原点
练习1
二、四
m<2
三
1.函数 的图象在第 象限。
2.双曲线 经过点(-3,___)。
3.函数 的图象在二、四象限,则m的取值范围是____。
4.对于函数 ,当x<0时,图象在第________象限。
5.已知反比例函数 的图像在二、四象限内,而一次函数y=mx+2的图象经过一、二、三象限,求m的取值范围。
6.在平面直角坐标系中有六个点A(1,5),B(-3,-1.5),C(-5,-1),D(2,2.5),E(3,5/3),F(2.5,2),其中有五个点在同一反比例函数图像上,在这个反比例函数图像上的点有( )。
例 已知反比例函数 。
(1)解:因为函数图象经过点(-3,5),代入函数的表达式,得:
(2)根据题意,有2k-1>0
(1)已知这个函数图象经过点(-3,5),求k的值;
(2)如果这个函数图象在它所处的象限内,函数y随x的增大而减小,求k的范围。
解方程,得:k=-7
解不等式,得:
1.下列反比例函数的图象分别在哪个象限?
做一做:
2.已知反比例函数 的图象上一点的坐标为( ,2),求这个反比例函数的解析式。
任意一组变量的乘积是一个定值,即xy=k。
P(m,n)
A
o
y
x
B
长方形面积:|mn|= | k |
三角形的面积:
面积不变性
梳理概括,形成结构
请大家围绕以下三个问题小结:
①什么是反比例函数?
②反比例函数的图象是什么样子的?怎样作图象?
③反比例函数的性质是什么?
形状
位置
变化趋势
对称性
面积不变性
y=
x
k
x
y
0
k>0
练习2
1.已知k<0,则函数y1=kx, 在同一坐标系中的图象大致是( )
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
D
2.已知k>0,则函数y1=kx+k与 在同一坐标系中的图象大致是( )
(A)
x
y
0
x
y
0
(B)
(C)
(D)
x
y
0
x
y
0
C
谢 谢
反比例函数
1.长方形的长为6,宽y和面积x之间有什么关系?
2.长方形的面积为6,一边长x和另一边长y之间有什么关系?
xy=6
写出下列各关系式:
两个相关联的量,一个量变化,另一个量也随着变化。
如果两个变量的积是一个不为零的常数,我们就说这两个变量成反比例。
正比例
反比例
xy=6
1.北京到杭州的铁路线长为1661km。一列火车从北京开往杭州,记火车全程的行驶时间为x(h),火车行驶的平均速度为y(km/h)。
x(h) 12 15 17 22
y(km/h) 87.4
(2)y与x成什么比例关系?能用一个数学解析式表示吗?
138.4
97.7
110.7
75.5
19
成反比例关系
xy=1661
(1)你能完成下列表格吗?
2.学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为24平方米的矩形饲养场。设它的一边长为x(米),请写出另一边的长y(米)与x的关系式。
解:由题意得:
x
y
xy=24
发现
一般地,若变量y与x成反比例,则有xy=k
(k为常数,k≠0),
其中x是自变量,y是x的函数,k叫做比例系数。
形如 (k是常数,k≠0)的函数叫做反比例函数。
巩固练习:
(1)y=-3x
1.下列函数中,哪些y是x的反比例函数?并说出反比例函数的比例系数:
不是反比例函数
不是反比例函数
是反比例函数,比例系数为5。
是反比例函数,比例系数为-6。
是反比例函数,比例系数为 。
不是反比例函数
2.已知反比例函数 。
(1)说出比例系数;
(2)求当x=-10时函数的值;
(3)求当y=2.5时自变量x的值。
解:(1)比例系数是 。
(2)当x=-10时,
(3)当y=2.5时,
3.设面积为10cm的三角形的一边长为a(cm),这条边上的高为h(cm)。
(3)求当边长a=2.5cm时,这条边上的高。
(2)h关于a的函数是不是反比例函数?如果是,请说出它的比例系数。
(1)求h关于a的函数解析式及自变量a的取值范围;
给我一个支点,我可以撬动地球!
——阿基米德
背景知识
阻力×阻力臂=动力×动力臂
阻力臂
阻力
动力臂
动力
背景知识
杠杆定律
(1)求y关于x的函数解析式。这个函数是反比例函数吗?如果是,请说出比例系数。
【例】如图,阻力为1000N,阻力臂长为5cm。设动力为y(N),动力臂为x(cm)。(图中杠杆本身所受重力略去不计。杠杆平衡时,动力×动力臂=阻力×阻力臂)
解:根据题意,得y×x=1000×5
所以所求函数的解析式为
这个函数是反比例函数,比例系数为5000。
(2)求当x=50时函数y的值,并说明这个值的实际意义。
解:当x=50时,
这个函数值的实际意义是,当动力臂长为50cm时,所需动力为100N。
(3)利用y关于x的函数解析式,说明当动力臂长扩大到原来的n(n>1)倍时,所需动力将怎样变化?
解:设原来的动力臂长为d(cm),动力为y1(N);扩大后的动力臂长为nd(cm)(n>1),动力为y2(N)。
将x=d,x=nd分别代入
所以当动力臂长扩大到原来的n倍时,所需动力缩小到原来的 。
知者先行:
1.当m为何值时,函数 是反比例函数,并求出其函数解析式。
2.若是函数 是反比例函数,求此反比例函数的关系式。
3.设y=y1+y2,且y1与x成正比例,y2与x成反比例。当x=1时,y=1;当x=2时,y=-1。
(1)求y与x的关系式;(2)求当x=3时,y的值。
归纳
(1)k叫做反比例函数的比例系数;
(2)反比例函数的自变量x的值不能为零。
(3)反比例函数的确定:待定系数法。
(4) 常见的表达形式:xy=k(k≠0)、y=kx-1(k≠0)。
形如 ( k是常数,k≠0 )的函数叫做反比例函数。
1.下列函数中哪些是y关于x的反比例函数?
①y=3x-1;②y=2x-1;③ ④
⑤ ⑥ ⑦ ⑧
2.已知△ABC的面积为12,则△ABC的高h与它的底边a的函数关系式为 。
3.已知y是x的反比例函数,下表给出了x和y的一些值:
x -2 -1 1 3
y 2 -1
(1)求出这个反比例函数的解析式: 。
思考:表中能否增加x=0或y=0的值,为什么?
(2)根据函数解析式完成上表。
1
-2
2
函数图象画法
列
表
描
点
连
线
描点法
反比例函数的图象又会是什么样子呢?
你还记得作函数图象的一般步骤吗?
用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线(按自变量从小到大的顺序,用一条平滑的曲线连接起来)。
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
y=
x
6
y=
x
6
列
表
描
点
连
线
描点法
注意:一般情况取8个点。
例 画出反比例函数 和 的函数图象。
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
x
x
y =
x
6
y =
x
6
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
x
y
1
6
2
3
3
2
4
1.5
5
1.2
6
1
6
-1
-6
-2
-3
-3
-1.5
-2
-4
-5
-1.2
-6
-1
…
…
…
…
-6
6
3
-3
2
-2
1.5
-1.5
1.2
-1.2
1
-1
…
…
y =
x
6
y =
x
6
从画反比例函数图象看,描点法还应注意什么?
反比例函数图象画法步骤:
列
表
描
点
连
线
描点法
注意:①列x与y的对应值表时, x的值不能为零,但仍可以零的基础,左右均匀、对称地取值。
至少左右各4个。
注意:②描点时自左往右用光滑曲线顺次连结,切忌用折线。
注意:③两个分支合起来才是反比例函数图象。两个分支不能到达x轴、y轴。
2.反比例函数 的图象在哪两个象限?由什么确定?
3.反比例函数 具有怎样的对称性?
4.反比例函数 的图象的变化趋势是怎样的,它和两条坐标轴的位置关系是怎样的?
1.反比例函数 和 的图象在哪两个象限?它们相同吗?
y=
x
6
x
y
0
y
x
x
6
y=
0
议一议
讨论
1.当k>0时,图象的两个分支分别在第一、三象限内,y随x的增大而减小。
2.当k<0时,图象的两个分支分别在第二、四象限内,y随x的增大而增大。
y=
x
6
x
y
0
y
x
x
6
y=
0
3.图象的两个分支关于直角坐标系的原点成中心对称。
如果知道双曲线的一支,利用对称性,如何画另一支?
4.双曲线无限接近于x、y轴,但永远不会与坐标轴相交。
你能总结一下反比例函数的图象性质特征吗?
图象是双曲线
当k>0时,双曲线分别位于第一、三象限内
当k<0时,双曲线分别位于第二、四象限内
双曲线是中心对称图形
形状
位置
变化趋势
对称性
双曲线无限接近于x、y轴,但永远不会与坐标轴相交
对称中心
坐标原点
练习1
二、四
m<2
三
1.函数 的图象在第 象限。
2.双曲线 经过点(-3,___)。
3.函数 的图象在二、四象限,则m的取值范围是____。
4.对于函数 ,当x<0时,图象在第________象限。
5.已知反比例函数 的图像在二、四象限内,而一次函数y=mx+2的图象经过一、二、三象限,求m的取值范围。
6.在平面直角坐标系中有六个点A(1,5),B(-3,-1.5),C(-5,-1),D(2,2.5),E(3,5/3),F(2.5,2),其中有五个点在同一反比例函数图像上,在这个反比例函数图像上的点有( )。
例 已知反比例函数 。
(1)解:因为函数图象经过点(-3,5),代入函数的表达式,得:
(2)根据题意,有2k-1>0
(1)已知这个函数图象经过点(-3,5),求k的值;
(2)如果这个函数图象在它所处的象限内,函数y随x的增大而减小,求k的范围。
解方程,得:k=-7
解不等式,得:
1.下列反比例函数的图象分别在哪个象限?
做一做:
2.已知反比例函数 的图象上一点的坐标为( ,2),求这个反比例函数的解析式。
任意一组变量的乘积是一个定值,即xy=k。
P(m,n)
A
o
y
x
B
长方形面积:|mn|= | k |
三角形的面积:
面积不变性
梳理概括,形成结构
请大家围绕以下三个问题小结:
①什么是反比例函数?
②反比例函数的图象是什么样子的?怎样作图象?
③反比例函数的性质是什么?
形状
位置
变化趋势
对称性
面积不变性
y=
x
k
x
y
0
k>0
练习2
1.已知k<0,则函数y1=kx, 在同一坐标系中的图象大致是( )
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
D
2.已知k>0,则函数y1=kx+k与 在同一坐标系中的图象大致是( )
(A)
x
y
0
x
y
0
(B)
(C)
(D)
x
y
0
x
y
0
C
谢 谢
