第六章 匀速圆周运动的几个模型 期末检测题(Word版含答案)
文档属性
| 名称 | 第六章 匀速圆周运动的几个模型 期末检测题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 581.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-29 12:25:21 | ||
图片预览


文档简介
匀速圆周运动的几个模型
1. 单选题
1.如图所示为公路自行车赛中运动员在水平路面上急转弯时的情景,运动员在通过弯道时如果控制不当会发生侧滑而摔离正常比赛路线,将运动员与自行车看做一个整体,下列论述正确的是( )
A.运动员转弯所需向心力由地面对车轮的支持力与重力的合力提供
B.运动员转弯所需向心力由地面对车轮的摩擦力提供
C.发生侧滑是因为运动员受到的合力方向背离圆心
D.发生侧滑是因为运动员受到的合力大于所需的向心力
2.如图(a)中甲汽车在水平路面上转弯行驶,图(b)中乙汽车在倾斜路面上转弯行驶.关于两辆汽车的受力情况,以下说法正确的是( )
A.两车都受到路面竖直向上的支持力作用
B.两车都一定受平行路面指向弯道内侧的摩擦力
C.甲车可能不受平行路面指向弯道内侧的摩擦力
D.乙车可能受平行路面指向弯道外侧的摩擦力
3.洗衣机的脱水筒如图所示,设其半径为R并绕竖直轴线OO′以角速度ω匀速转动.质量不同的小物件A、B随脱水筒转动且相对筒壁静止,两小物体与筒壁间的动摩擦因数相同,最大静摩擦力等于滑动摩擦力.则( )
A.转速减小,质量大的物件先下落
B.转速增加,物件对筒壁的压力均增加
C.转速增加,物件受到的摩擦力均增加
D.转动过程中两物件的向心加速度总是相同
4.一辆汽车匀速率通过一座圆弧形拱桥后,接着又以相同速率通过一圆弧形凹形桥.设两圆弧半径相等,汽车通过拱桥桥顶时,对桥面的压力F1为车重的一半,汽车通过圆弧形凹形桥的最低点时,对桥面的压力为F2,则F1与F2之比为( )
A.1∶1 B.1∶2 C.1∶3 D.2∶1
5.如图所示,一个圆形框架以竖直的直径为转轴匀速转动。在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止。下列说法正确的是( )
A.小球A的合力小于小球B的合力
B.小球A与框架间可能没有摩擦力
C.小球B与框架间可能没有摩擦力
D.圆形框架以更大的角速度转动,小球B受到的摩擦力一定增大
2. 多选题
6.在修筑铁路时,弯道处的外轨会略高于内轨.如图所示,当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时的速度大小为v,重力加速度为g,两轨所在面的倾角为θ,则( )
A.该弯道的半径r=
B.当火车质量改变时,规定的行驶速度大小不变
C.当火车速率大于v时,内轨将受到轮缘的挤压
D.当火车速率大于v时,外轨将受到轮缘的挤压
7.如图所示,一轻绳穿过水平桌面上的小圆孔,上端拴物体M,下端拴物体N。若物体M在桌面上做半径为r的匀速圆周运动时,角速度为ω,线速度大小为v,物体N处于静止状态,则(不计摩擦)( )
A.M所需向心力大小等于N所受重力的大小
B.M所需向心力大小大于N所受重力的大小
C.v2与r成正比
D.ω2与r成正比
8.两根长度不同的细线下面分别悬挂两个完全相同的小球A、B,细线上端固定在同一点,绕共同的竖直轴在水平面内做匀速圆周运动。已知A球细线L1跟竖直方向的夹角为30°,B球细线L2跟竖直方向的夹角为60°,下列说法正确的是( )
A.细线L1和细线L2所受的拉力大小之比为∶1
B.小球A和B的向心力大小之比为1∶3
C.小球A和B的角速度大小之比为1∶1
D.小球A和B的线速度大小之比为1∶
9.如图内壁光滑的玻璃管内用长为L的轻绳悬挂一个小球。当玻璃管绕竖直轴以角速度ω匀速转动时,小球与玻璃管间恰无压力。下列说法正确的是( )
A.仅增加绳长后,小球将受到玻璃管斜向上方的压力
B.仅增加绳长后,若仍保持小球与玻璃管间无压力,需减小ω
C.仅增加小球质量后,小球将受到玻璃管斜向上方的压力
D.仅增加角速度至ω′后,小球将受到玻璃管斜向下方的压力
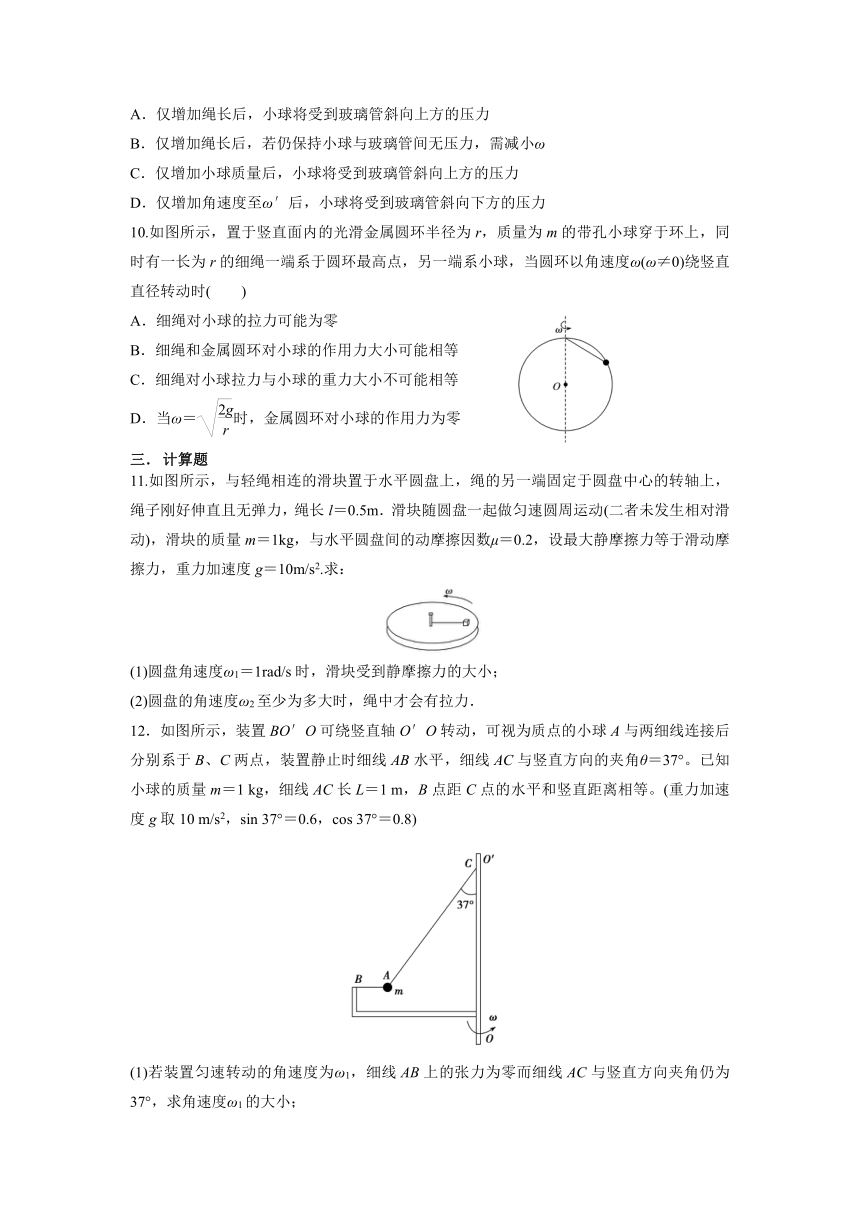
10.如图所示,置于竖直面内的光滑金属圆环半径为r,质量为m的带孔小球穿于环上,同时有一长为r的细绳一端系于圆环最高点,另一端系小球,当圆环以角速度ω(ω≠0)绕竖直直径转动时( )
A.细绳对小球的拉力可能为零
B.细绳和金属圆环对小球的作用力大小可能相等
C.细绳对小球拉力与小球的重力大小不可能相等
D.当ω=时,金属圆环对小球的作用力为零
3. 计算题
11.如图所示,与轻绳相连的滑块置于水平圆盘上,绳的另一端固定于圆盘中心的转轴上,绳子刚好伸直且无弹力,绳长l=0.5m.滑块随圆盘一起做匀速圆周运动(二者未发生相对滑动),滑块的质量m=1kg,与水平圆盘间的动摩擦因数μ=0.2,设最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2.求:
(1)圆盘角速度ω1=1rad/s时,滑块受到静摩擦力的大小;
(2)圆盘的角速度ω2至少为多大时,绳中才会有拉力.
12.如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°。已知小球的质量m=1 kg,细线AC长L=1 m,B点距C点的水平和竖直距离相等。(重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8)
(1)若装置匀速转动的角速度为ω1,细线AB上的张力为零而细线AC与竖直方向夹角仍为37°,求角速度ω1的大小;
(2)若装置匀速转动的角速度为ω2时,细线AB刚好竖直,且张力为零,求此时角速度ω2的大小。
匀速圆周运动的几个模型
4. 单选题
1.答案 B解析 向心力为沿半径方向上的合力.运动员转弯时,受力分析如图所示,可知地面对车轮的摩擦力提供所需的向心力,故A错误,B正确;当Ff<,摩擦力不足以提供所需向心力时,就会发生离心侧滑,故C、D错误.
2.答案 D解析 水平路面上的汽车在竖直方向上受竖直向上的支持力和竖直向下的重力,倾斜路面上汽车受到的支持力与倾斜路面垂直,故A错误.汽车转弯时的运动可看成圆周运动,向心力方向指向弯道内侧,令倾斜路面的倾角为θ,当乙车的速度满足m=mgtanθ,即v=,乙车恰好没有向路面内外两侧滑动的趋势,即此时乙车不受摩擦力作用;乙车在倾斜路面转弯,当速度大于时,重力与支持力的合力不足以提供向心力,这时乙车有向外运动的趋势,所以乙车受到路面的摩擦力指向弯道内侧;当速度小于时,重力与支持力的合力大于所需向心力,乙车有向里运动的趋势,此时乙车受到平行路面指向弯道外侧的摩擦力作用,故B错误,D正确.甲车转弯时,由静摩擦力提供做圆周运动所需的向心力,故甲车不可能不受平行于路面指向弯道内侧的摩擦力,故C错误.
3.答案 B解析 物件恰不下落时,对物件受力分析,水平方向:FN=mω2r;竖直方向:mg=μFN,即g=μω2r,则与衣物的质量无关,即转速减小,物件同时下落,选项A错误;由FN=mω2r可知,转速增加,物件对筒壁的压力均增加,选项B正确;物件所受的摩擦力等于重力,可知转速增加,物件受到的摩擦力不变,选项C错误;转动过程中两物件的向心加速度大小相同,但是方向不一定相同,选项D错误.
4.C
5.C解析:小球受到的合力充当向心力,因为到竖直转轴的距离相等,所以两小球的速度大小相等,半径相同,根据公式F合=m可知,两小球受到的合力大小相等,A错误;小球A受到的重力竖直向下,受到的支持力垂直该点圆环切线方向指向圆心,故两个力的合力不可能指向竖直转轴,所以一定受到摩擦力作用,小球B受到竖直向下的重力和垂直该点切线方向指向圆心的支持力,合力可能指向竖直转轴,所以B可能不受摩擦力作用,B错误,C正确;因为B可能不受摩擦力作用,所以无法判断摩擦力变化,故D错误。
5. 多选题
6.答案 ABD解析 火车转弯时不侧向挤压车轮轮缘,靠重力和支持力的合力提供向心力,根据牛顿第二定律有:mgtanθ=m,解得:r=,故A正确;根据牛顿第二定律有:mgtanθ=m,解得:v=,可知火车规定的行驶速度与质量无关,故B正确;当火车速率大于v时,重力和支持力的合力不足以提供向心力,此时外轨对火车有侧压力,轮缘挤压外轨,故C错误,D正确.
7.答案:AC解析:N物体静止不动,绳子拉力与N物体重力相等,M物体做匀速圆周运动,绳子拉力完全提供向心力,即T=mNg=F向,所以M所需向心力大小等于N所受重力的大小,A正确,B错误;
根据向心加速度公式和牛顿第二定律得
F向=mNg=m
则v2与r成正比,C正确;
根据向心加速度公式和牛顿第二定律得
F向=mNg=mω2r
则ω2与r成反比,D错误。
8.答案:BC解析:两球在水平面内做圆周运动,在竖直方向上的合力为零,有FTAcos 30°=mg,FTBcos 60°=mg,则FTA==,FTB=2mg,所以FTA∶FTB=∶3=1∶,故A错误;小球A做圆周运动的向心力FnA=mgtan 30°=mg,小球B做圆周运动的向心力FnB=mgtan 60°=mg,可知小球A、B的向心力大小之比为1∶3,故B正确;根据mgtan θ=m·htan θ·ω2=m 得,角速度ω=,线速度v=tan θ,可知角速度之比为1∶1,线速度大小之比为1∶3,故C正确,D错误。
9.答案:BD解析:根据题意可知,mgtan θ=mrω2=mLω2sin θ,仅增加绳长后,小球需要的向心力变大,则有离心趋势,会挤压管壁右侧,小球受到玻璃管斜向下方的压力,故A错误;仅增加绳长后,若仍保持小球与玻璃管间无压力,根据以上分析可知,需减小ω,故B正确;小球质量可以被约去,所以,增加小球质量,小球仍与管壁间无压力,故C错误;仅增加角速度至ω′后,小球需要向心力变大,则有离心趋势,会挤压管壁右侧,小球受到玻璃管斜向下方的压力,故D正确。
10.答案 CD
解析 圆环光滑,小球受到重力、环对球的弹力和绳子的拉力,根据几何关系可知,此时细绳与竖直方向的夹角为60°,当圆环旋转时,小球绕竖直轴做圆周运动,则有FTcos 60°+FNcos60°=mg,FTsin60°-FNsin60°=mω2rsin60°,解得FT=mg+mω2r,FN=mg-mω2r, 当ω=时,金属圆环对小球的作用力FN=0,故C、D正确,A、B错误.
6. 计算题
11.如图17所示,与轻绳相连的滑块置于水平圆盘上,绳的另一端固定于圆盘中心的转轴上,绳子刚好伸直且无弹力,绳长l=0.5m.滑块随圆盘一起做匀速圆周运动(二者未发生相对滑动),滑块的质量m=1kg,与水平圆盘间的动摩擦因数μ=0.2,设最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2.求:
图17
(1)圆盘角速度ω1=1rad/s时,滑块受到静摩擦力的大小;
(2)圆盘的角速度ω2至少为多大时,绳中才会有拉力.
答案 (1)0.5N (2)2rad/s
解析 (1)静摩擦力提供向心力,有:Ff=mω12l,代入数据解得:Ff=0.5N
(2)当静摩擦力达到最大值时,绳中才出现拉力,最大静摩擦力提供向心力,有:μmg=mω22l,代入数据解得:ω2=2rad/s.
12.如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°。已知小球的质量m=1 kg,细线AC长L=1 m,B点距C点的水平和竖直距离相等。(重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8)
(1)若装置匀速转动的角速度为ω1,细线AB上的张力为零而细线AC与竖直方向夹角仍为37°,求角速度ω1的大小;
(2)若装置匀速转动的角速度为ω2时,细线AB刚好竖直,且张力为零,求此时角速度ω2的大小。
解析:(1)细线AB上的张力恰为零时有
mgtan 37°=mωLsin 37°,
解得ω1= = rad/s= rad/s。
(2)细线AB恰好竖直,但张力为零时,由几何关系得
cos θ′=,则有θ′=53°,
又mgtan θ′=mωLsin θ′,
解得ω2= rad/s。
答案:(1) rad/s (2) rad/s
1. 单选题
1.如图所示为公路自行车赛中运动员在水平路面上急转弯时的情景,运动员在通过弯道时如果控制不当会发生侧滑而摔离正常比赛路线,将运动员与自行车看做一个整体,下列论述正确的是( )
A.运动员转弯所需向心力由地面对车轮的支持力与重力的合力提供
B.运动员转弯所需向心力由地面对车轮的摩擦力提供
C.发生侧滑是因为运动员受到的合力方向背离圆心
D.发生侧滑是因为运动员受到的合力大于所需的向心力
2.如图(a)中甲汽车在水平路面上转弯行驶,图(b)中乙汽车在倾斜路面上转弯行驶.关于两辆汽车的受力情况,以下说法正确的是( )
A.两车都受到路面竖直向上的支持力作用
B.两车都一定受平行路面指向弯道内侧的摩擦力
C.甲车可能不受平行路面指向弯道内侧的摩擦力
D.乙车可能受平行路面指向弯道外侧的摩擦力
3.洗衣机的脱水筒如图所示,设其半径为R并绕竖直轴线OO′以角速度ω匀速转动.质量不同的小物件A、B随脱水筒转动且相对筒壁静止,两小物体与筒壁间的动摩擦因数相同,最大静摩擦力等于滑动摩擦力.则( )
A.转速减小,质量大的物件先下落
B.转速增加,物件对筒壁的压力均增加
C.转速增加,物件受到的摩擦力均增加
D.转动过程中两物件的向心加速度总是相同
4.一辆汽车匀速率通过一座圆弧形拱桥后,接着又以相同速率通过一圆弧形凹形桥.设两圆弧半径相等,汽车通过拱桥桥顶时,对桥面的压力F1为车重的一半,汽车通过圆弧形凹形桥的最低点时,对桥面的压力为F2,则F1与F2之比为( )
A.1∶1 B.1∶2 C.1∶3 D.2∶1
5.如图所示,一个圆形框架以竖直的直径为转轴匀速转动。在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止。下列说法正确的是( )
A.小球A的合力小于小球B的合力
B.小球A与框架间可能没有摩擦力
C.小球B与框架间可能没有摩擦力
D.圆形框架以更大的角速度转动,小球B受到的摩擦力一定增大
2. 多选题
6.在修筑铁路时,弯道处的外轨会略高于内轨.如图所示,当火车以规定的行驶速度转弯时,内、外轨均不会受到轮缘的挤压,设此时的速度大小为v,重力加速度为g,两轨所在面的倾角为θ,则( )
A.该弯道的半径r=
B.当火车质量改变时,规定的行驶速度大小不变
C.当火车速率大于v时,内轨将受到轮缘的挤压
D.当火车速率大于v时,外轨将受到轮缘的挤压
7.如图所示,一轻绳穿过水平桌面上的小圆孔,上端拴物体M,下端拴物体N。若物体M在桌面上做半径为r的匀速圆周运动时,角速度为ω,线速度大小为v,物体N处于静止状态,则(不计摩擦)( )
A.M所需向心力大小等于N所受重力的大小
B.M所需向心力大小大于N所受重力的大小
C.v2与r成正比
D.ω2与r成正比
8.两根长度不同的细线下面分别悬挂两个完全相同的小球A、B,细线上端固定在同一点,绕共同的竖直轴在水平面内做匀速圆周运动。已知A球细线L1跟竖直方向的夹角为30°,B球细线L2跟竖直方向的夹角为60°,下列说法正确的是( )
A.细线L1和细线L2所受的拉力大小之比为∶1
B.小球A和B的向心力大小之比为1∶3
C.小球A和B的角速度大小之比为1∶1
D.小球A和B的线速度大小之比为1∶
9.如图内壁光滑的玻璃管内用长为L的轻绳悬挂一个小球。当玻璃管绕竖直轴以角速度ω匀速转动时,小球与玻璃管间恰无压力。下列说法正确的是( )
A.仅增加绳长后,小球将受到玻璃管斜向上方的压力
B.仅增加绳长后,若仍保持小球与玻璃管间无压力,需减小ω
C.仅增加小球质量后,小球将受到玻璃管斜向上方的压力
D.仅增加角速度至ω′后,小球将受到玻璃管斜向下方的压力
10.如图所示,置于竖直面内的光滑金属圆环半径为r,质量为m的带孔小球穿于环上,同时有一长为r的细绳一端系于圆环最高点,另一端系小球,当圆环以角速度ω(ω≠0)绕竖直直径转动时( )
A.细绳对小球的拉力可能为零
B.细绳和金属圆环对小球的作用力大小可能相等
C.细绳对小球拉力与小球的重力大小不可能相等
D.当ω=时,金属圆环对小球的作用力为零
3. 计算题
11.如图所示,与轻绳相连的滑块置于水平圆盘上,绳的另一端固定于圆盘中心的转轴上,绳子刚好伸直且无弹力,绳长l=0.5m.滑块随圆盘一起做匀速圆周运动(二者未发生相对滑动),滑块的质量m=1kg,与水平圆盘间的动摩擦因数μ=0.2,设最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2.求:
(1)圆盘角速度ω1=1rad/s时,滑块受到静摩擦力的大小;
(2)圆盘的角速度ω2至少为多大时,绳中才会有拉力.
12.如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°。已知小球的质量m=1 kg,细线AC长L=1 m,B点距C点的水平和竖直距离相等。(重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8)
(1)若装置匀速转动的角速度为ω1,细线AB上的张力为零而细线AC与竖直方向夹角仍为37°,求角速度ω1的大小;
(2)若装置匀速转动的角速度为ω2时,细线AB刚好竖直,且张力为零,求此时角速度ω2的大小。
匀速圆周运动的几个模型
4. 单选题
1.答案 B解析 向心力为沿半径方向上的合力.运动员转弯时,受力分析如图所示,可知地面对车轮的摩擦力提供所需的向心力,故A错误,B正确;当Ff<,摩擦力不足以提供所需向心力时,就会发生离心侧滑,故C、D错误.
2.答案 D解析 水平路面上的汽车在竖直方向上受竖直向上的支持力和竖直向下的重力,倾斜路面上汽车受到的支持力与倾斜路面垂直,故A错误.汽车转弯时的运动可看成圆周运动,向心力方向指向弯道内侧,令倾斜路面的倾角为θ,当乙车的速度满足m=mgtanθ,即v=,乙车恰好没有向路面内外两侧滑动的趋势,即此时乙车不受摩擦力作用;乙车在倾斜路面转弯,当速度大于时,重力与支持力的合力不足以提供向心力,这时乙车有向外运动的趋势,所以乙车受到路面的摩擦力指向弯道内侧;当速度小于时,重力与支持力的合力大于所需向心力,乙车有向里运动的趋势,此时乙车受到平行路面指向弯道外侧的摩擦力作用,故B错误,D正确.甲车转弯时,由静摩擦力提供做圆周运动所需的向心力,故甲车不可能不受平行于路面指向弯道内侧的摩擦力,故C错误.
3.答案 B解析 物件恰不下落时,对物件受力分析,水平方向:FN=mω2r;竖直方向:mg=μFN,即g=μω2r,则与衣物的质量无关,即转速减小,物件同时下落,选项A错误;由FN=mω2r可知,转速增加,物件对筒壁的压力均增加,选项B正确;物件所受的摩擦力等于重力,可知转速增加,物件受到的摩擦力不变,选项C错误;转动过程中两物件的向心加速度大小相同,但是方向不一定相同,选项D错误.
4.C
5.C解析:小球受到的合力充当向心力,因为到竖直转轴的距离相等,所以两小球的速度大小相等,半径相同,根据公式F合=m可知,两小球受到的合力大小相等,A错误;小球A受到的重力竖直向下,受到的支持力垂直该点圆环切线方向指向圆心,故两个力的合力不可能指向竖直转轴,所以一定受到摩擦力作用,小球B受到竖直向下的重力和垂直该点切线方向指向圆心的支持力,合力可能指向竖直转轴,所以B可能不受摩擦力作用,B错误,C正确;因为B可能不受摩擦力作用,所以无法判断摩擦力变化,故D错误。
5. 多选题
6.答案 ABD解析 火车转弯时不侧向挤压车轮轮缘,靠重力和支持力的合力提供向心力,根据牛顿第二定律有:mgtanθ=m,解得:r=,故A正确;根据牛顿第二定律有:mgtanθ=m,解得:v=,可知火车规定的行驶速度与质量无关,故B正确;当火车速率大于v时,重力和支持力的合力不足以提供向心力,此时外轨对火车有侧压力,轮缘挤压外轨,故C错误,D正确.
7.答案:AC解析:N物体静止不动,绳子拉力与N物体重力相等,M物体做匀速圆周运动,绳子拉力完全提供向心力,即T=mNg=F向,所以M所需向心力大小等于N所受重力的大小,A正确,B错误;
根据向心加速度公式和牛顿第二定律得
F向=mNg=m
则v2与r成正比,C正确;
根据向心加速度公式和牛顿第二定律得
F向=mNg=mω2r
则ω2与r成反比,D错误。
8.答案:BC解析:两球在水平面内做圆周运动,在竖直方向上的合力为零,有FTAcos 30°=mg,FTBcos 60°=mg,则FTA==,FTB=2mg,所以FTA∶FTB=∶3=1∶,故A错误;小球A做圆周运动的向心力FnA=mgtan 30°=mg,小球B做圆周运动的向心力FnB=mgtan 60°=mg,可知小球A、B的向心力大小之比为1∶3,故B正确;根据mgtan θ=m·htan θ·ω2=m 得,角速度ω=,线速度v=tan θ,可知角速度之比为1∶1,线速度大小之比为1∶3,故C正确,D错误。
9.答案:BD解析:根据题意可知,mgtan θ=mrω2=mLω2sin θ,仅增加绳长后,小球需要的向心力变大,则有离心趋势,会挤压管壁右侧,小球受到玻璃管斜向下方的压力,故A错误;仅增加绳长后,若仍保持小球与玻璃管间无压力,根据以上分析可知,需减小ω,故B正确;小球质量可以被约去,所以,增加小球质量,小球仍与管壁间无压力,故C错误;仅增加角速度至ω′后,小球需要向心力变大,则有离心趋势,会挤压管壁右侧,小球受到玻璃管斜向下方的压力,故D正确。
10.答案 CD
解析 圆环光滑,小球受到重力、环对球的弹力和绳子的拉力,根据几何关系可知,此时细绳与竖直方向的夹角为60°,当圆环旋转时,小球绕竖直轴做圆周运动,则有FTcos 60°+FNcos60°=mg,FTsin60°-FNsin60°=mω2rsin60°,解得FT=mg+mω2r,FN=mg-mω2r, 当ω=时,金属圆环对小球的作用力FN=0,故C、D正确,A、B错误.
6. 计算题
11.如图17所示,与轻绳相连的滑块置于水平圆盘上,绳的另一端固定于圆盘中心的转轴上,绳子刚好伸直且无弹力,绳长l=0.5m.滑块随圆盘一起做匀速圆周运动(二者未发生相对滑动),滑块的质量m=1kg,与水平圆盘间的动摩擦因数μ=0.2,设最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2.求:
图17
(1)圆盘角速度ω1=1rad/s时,滑块受到静摩擦力的大小;
(2)圆盘的角速度ω2至少为多大时,绳中才会有拉力.
答案 (1)0.5N (2)2rad/s
解析 (1)静摩擦力提供向心力,有:Ff=mω12l,代入数据解得:Ff=0.5N
(2)当静摩擦力达到最大值时,绳中才出现拉力,最大静摩擦力提供向心力,有:μmg=mω22l,代入数据解得:ω2=2rad/s.
12.如图所示,装置BO′O可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°。已知小球的质量m=1 kg,细线AC长L=1 m,B点距C点的水平和竖直距离相等。(重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8)
(1)若装置匀速转动的角速度为ω1,细线AB上的张力为零而细线AC与竖直方向夹角仍为37°,求角速度ω1的大小;
(2)若装置匀速转动的角速度为ω2时,细线AB刚好竖直,且张力为零,求此时角速度ω2的大小。
解析:(1)细线AB上的张力恰为零时有
mgtan 37°=mωLsin 37°,
解得ω1= = rad/s= rad/s。
(2)细线AB恰好竖直,但张力为零时,由几何关系得
cos θ′=,则有θ′=53°,
又mgtan θ′=mωLsin θ′,
解得ω2= rad/s。
答案:(1) rad/s (2) rad/s
