第六章 竖直平面内圆周运动 期末检测题(Word版含答案)
文档属性
| 名称 | 第六章 竖直平面内圆周运动 期末检测题(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-29 12:27:44 | ||
图片预览




文档简介
竖直平面内圆周运动
一、多选题
1.如图,摩天轮悬挂的座舱在竖直平面内做匀速圆周运动。关于座舱内某一游客( )
A.其所受合力指向轨迹圆心
B.他与座舱和地球组成的系统机械能守恒
C.从最高点到最低点过程中,所受摩擦力保持不变
D.在最低点、最高点对座椅的压力之差随转速减小而减小
2.如图所示,轻质硬杆的一端固定在竖直墙面的О点,可绕О点在竖直面内无摩擦地自由转动,另一端连接一个质量为m的小球P,重力加速度为g。小球在竖直面内做圆周运动的过程中,在最低点时与在最高点时对轻杆弹力大小之差可能为( )
A.3.8mg B.4.5mg C.5.6mg D.7.7mg
二、单选题
3.用长为L的轻质细绳系着个质量为m的小球,在竖直面内绕O点做圆周运动,小球经过最高点A时,细绳受到的拉力恰好等于小球的重力,已知重力加速度为g,则小球经过最高点A的速度大小为( )
A. B. C. D.
4.在山地越野赛中,质量为的汽车以恒定的速率运动。如图所示,通过凹形路面最低处A时,汽车对路面的压力为;通过凸形路面最高处时,汽车对路面的压力为,重力加速度为。则( )
A. B. C. D.
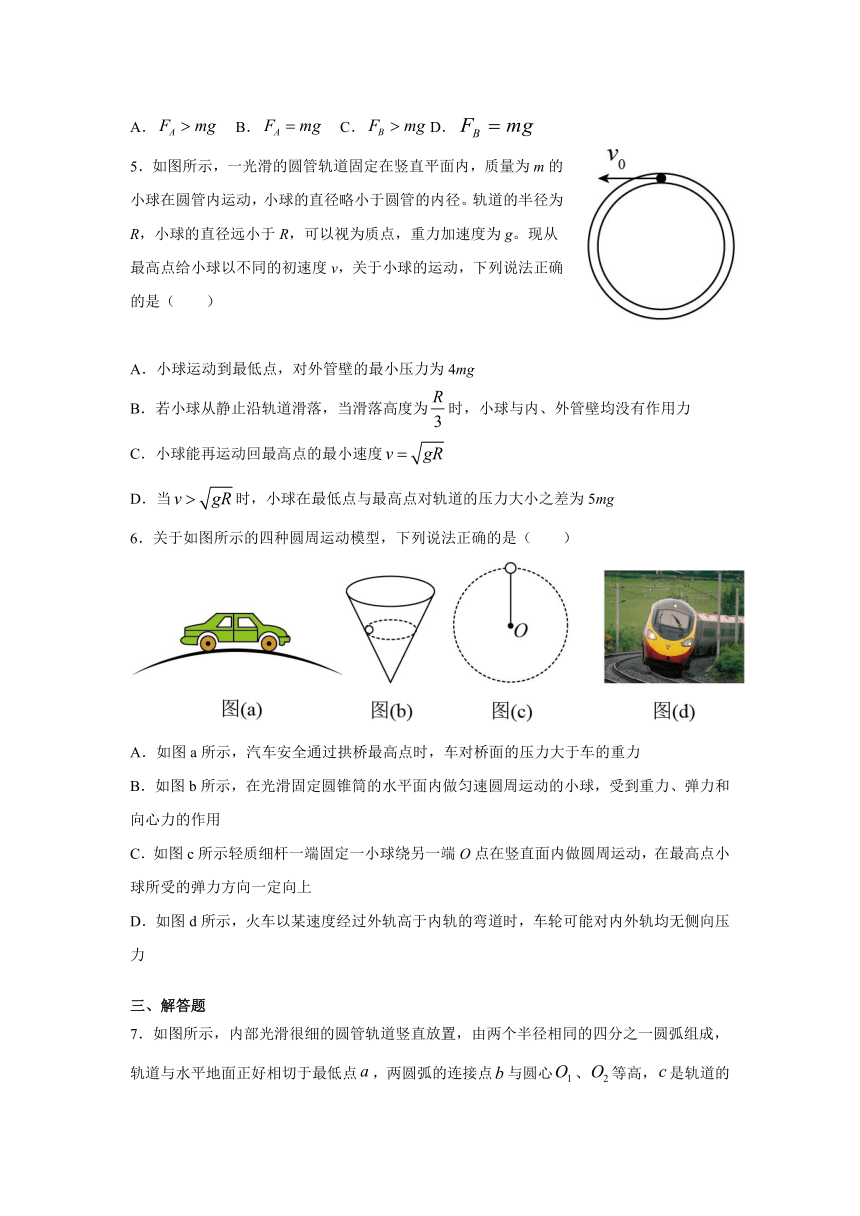
5.如图所示,一光滑的圆管轨道固定在竖直平面内,质量为m的小球在圆管内运动,小球的直径略小于圆管的内径。轨道的半径为R,小球的直径远小于R,可以视为质点,重力加速度为g。现从最高点给小球以不同的初速度v,关于小球的运动,下列说法正确的是( )
A.小球运动到最低点,对外管壁的最小压力为4mg
B.若小球从静止沿轨道滑落,当滑落高度为时,小球与内、外管壁均没有作用力
C.小球能再运动回最高点的最小速度
D.当时,小球在最低点与最高点对轨道的压力大小之差为5mg
6.关于如图所示的四种圆周运动模型,下列说法正确的是( )
A.如图a所示,汽车安全通过拱桥最高点时,车对桥面的压力大于车的重力
B.如图b所示,在光滑固定圆锥筒的水平面内做匀速圆周运动的小球,受到重力、弹力和向心力的作用
C.如图c所示轻质细杆一端固定一小球绕另一端O点在竖直面内做圆周运动,在最高点小球所受的弹力方向一定向上
D.如图d所示,火车以某速度经过外轨高于内轨的弯道时,车轮可能对内外轨均无侧向压力
三、解答题
7.如图所示,内部光滑很细的圆管轨道竖直放置,由两个半径相同的四分之一圆弧组成,轨道与水平地面正好相切于最低点,两圆弧的连接点与圆心、等高,是轨道的最高点;质量的小球,从点以某一水平速度进入管道,离开点时以某一初速度做平抛运动,落在地面上的点,重力加速度,求:
(1)若小球到达点时,管道的上壁对小球有向下的压力,则、两点对小球的弹力大小之差为多少;
(2)若小球在点的速度,在点的速度,求小球落地的速度与水平方向的夹角以及平抛运动的水平位移。
8.长L=0.5 m、质量可忽略的细杆,其一端可绕O点在竖直平面内转动,另一端固定着一个小球A的质量为m=2 kg。当A通过最高点时,如图所示,求在下列两种情况下杆对小球作用力的大小:
(1)A在最高点的速度为1 m/s;
(2)A在最高点的速度为4 m/s。
9.如图1所示,过山车在轨道上运行,可抽象为图2的模型。倾角为的直轨道、两个半径的竖直圆轨道和倾斜直轨道,分别通过水平轨道、平滑连接,、是两圆轨道最低点。长、长,足够长。质量为的过山车从上静止下滑,经两个圆环轨道后最终停在上。已知过山车与轨道、、的动摩擦因数均为,与圆轨道摩擦不计,。将过山车视为质点。
(1)若过山车恰能通过点,求其运动到点时对轨道的压力;
(2)若过山车恰能通过点,求释放点到的高度;
(3)若保障过山车不脱轨,求释放点到的高度范围。
竖直平面内圆周运动参考答案
1.AD
【详解】
A.游客随摩天轮在竖直平面内做匀速圆周运动,所受向心力的大小不变,方向指向轨迹的圆心,A正确;
B.在转动过程中,做匀速度圆周运动,他与座舱的动能不变,但高度在变化,重力势能在变化,所以机械能在变化,B错误;
D.设转速为n,在最高点时
在最低点时
则
D正确;
C.根据选项D分析可知,在转动过程中,游客对座舱的压力是不断变化的,所以摩擦力不断变化,C错误。
故选AD。
2.BC
【详解】
小球P做圆周运动,经过最高点时的速度设为。若
杆对小球的弹力向上,大小设为,根据向心力公式有
小球从最高点运动到最低点(速度设为),根据动能定理有
即
在最低点杆对小球的弹力大小为,应用向心力公式有
联立可得
结合
可得
若
在最高点杆对小球的弹力向下,大小设为,根据向心力公式有
在最低点有
联立可得
综合上述可知
AD错误,BC正确。
故选BC。
3.D
【详解】
根据
解得
故选D。
4.A
【详解】
AB.当汽车通过凹形路面最低处A时,根据圆周运动的性质可得
又汽车是以恒定的速度运动故可得,A正确,B错误;
CD.当汽车通过凹形路面最低处A时,根据圆周运动的性质可得
又汽车是以恒定的速度运动,故可得,CD错误。
故选A。
5.B
【详解】
A.当在最高点速度为零时,到达最低点的速度最小,对外管壁的压力最小,则由机械能守恒
在最低点设外管壁对小球的支持力为F,由牛顿第二定律
联立解得
由牛顿第三定律得,小球对外管壁的压力最小为5mg,故A错误;
B.小球从静止沿轨道滑落,当滑落高度为时,由机械能守恒
设此时重力沿半径方向的分力为,由几何关系得
此时所需的向心力为
代入数据得
此时重力沿半径方向的分力恰好提供向心力,所以小球与内、外管壁均没有作用力,故B正确;
C.因为管内壁可以给小球支持力,所以小球在最高点的速度可以为零,故C错误;
D.若在最高点速度时,在最高点由牛顿第二定律
最高点到最低点机械能守恒
在最低点时由牛顿第二定律
联立解得
所以当时,小球在最低点与最高点对轨道的压力大小之差为,故D错误。
故选B。
6.D
【详解】
A.如图a,由于汽车做圆周运动,合力指向圆心,因此过拱桥的最高点时所受支持力小于重力,即车对桥面的压力小于车的重力,A错误;
B.如图b,在光滑固定圆锥筒的水平面内做匀速圆周运动的小球,受到重力、弹力,这两个力的合力提供小球做圆周运动的向心力,B错误;
C.如图c,小球在最高点时,若杆的弹力恰好为零,此时
可得
若速度大于,杆对小球的弹力向下,C错误;
D.如图d,设外轨与内轨所在斜面与水平地面夹角为,车轮若对内外轨均无侧向压力,此时
可得速度为
D正确。
故选D。
7.(1)6N(2)60°;0.87m
【详解】
(1)若小球到达点时,管道的上壁对小球有向下的压力,则设在C点的速度为vc,则
从a点到c点,由机械能守恒定律可知
在a点时
解得、两点对小球的弹力大小之差为
(2)若小球在点的速度,在点的速度,根据
可得
小球落地的速度与水平方向的夹角
则
θ=60°
平抛运动的水平位移
8.(1)16N;(2)44N
【详解】
(1)当A在最高点只受重力时,由
得
A在最高点的速度为1 m/s,时,杆对球有支持力,则根据牛顿第二定律
可得
(2) A在最高点的速度为4 m/s时,杆对球有拉力,根据牛顿第二定律
可得
9.(1);(2);(3)
【详解】
(1)对点
对到,由机械能守恒
对点
可得
(2)对从释放点到运动过程:根据动能定理
可得
(3)过山车最终停在上,所以过山车须经过两个圆轨道,则有
一、多选题
1.如图,摩天轮悬挂的座舱在竖直平面内做匀速圆周运动。关于座舱内某一游客( )
A.其所受合力指向轨迹圆心
B.他与座舱和地球组成的系统机械能守恒
C.从最高点到最低点过程中,所受摩擦力保持不变
D.在最低点、最高点对座椅的压力之差随转速减小而减小
2.如图所示,轻质硬杆的一端固定在竖直墙面的О点,可绕О点在竖直面内无摩擦地自由转动,另一端连接一个质量为m的小球P,重力加速度为g。小球在竖直面内做圆周运动的过程中,在最低点时与在最高点时对轻杆弹力大小之差可能为( )
A.3.8mg B.4.5mg C.5.6mg D.7.7mg
二、单选题
3.用长为L的轻质细绳系着个质量为m的小球,在竖直面内绕O点做圆周运动,小球经过最高点A时,细绳受到的拉力恰好等于小球的重力,已知重力加速度为g,则小球经过最高点A的速度大小为( )
A. B. C. D.
4.在山地越野赛中,质量为的汽车以恒定的速率运动。如图所示,通过凹形路面最低处A时,汽车对路面的压力为;通过凸形路面最高处时,汽车对路面的压力为,重力加速度为。则( )
A. B. C. D.
5.如图所示,一光滑的圆管轨道固定在竖直平面内,质量为m的小球在圆管内运动,小球的直径略小于圆管的内径。轨道的半径为R,小球的直径远小于R,可以视为质点,重力加速度为g。现从最高点给小球以不同的初速度v,关于小球的运动,下列说法正确的是( )
A.小球运动到最低点,对外管壁的最小压力为4mg
B.若小球从静止沿轨道滑落,当滑落高度为时,小球与内、外管壁均没有作用力
C.小球能再运动回最高点的最小速度
D.当时,小球在最低点与最高点对轨道的压力大小之差为5mg
6.关于如图所示的四种圆周运动模型,下列说法正确的是( )
A.如图a所示,汽车安全通过拱桥最高点时,车对桥面的压力大于车的重力
B.如图b所示,在光滑固定圆锥筒的水平面内做匀速圆周运动的小球,受到重力、弹力和向心力的作用
C.如图c所示轻质细杆一端固定一小球绕另一端O点在竖直面内做圆周运动,在最高点小球所受的弹力方向一定向上
D.如图d所示,火车以某速度经过外轨高于内轨的弯道时,车轮可能对内外轨均无侧向压力
三、解答题
7.如图所示,内部光滑很细的圆管轨道竖直放置,由两个半径相同的四分之一圆弧组成,轨道与水平地面正好相切于最低点,两圆弧的连接点与圆心、等高,是轨道的最高点;质量的小球,从点以某一水平速度进入管道,离开点时以某一初速度做平抛运动,落在地面上的点,重力加速度,求:
(1)若小球到达点时,管道的上壁对小球有向下的压力,则、两点对小球的弹力大小之差为多少;
(2)若小球在点的速度,在点的速度,求小球落地的速度与水平方向的夹角以及平抛运动的水平位移。
8.长L=0.5 m、质量可忽略的细杆,其一端可绕O点在竖直平面内转动,另一端固定着一个小球A的质量为m=2 kg。当A通过最高点时,如图所示,求在下列两种情况下杆对小球作用力的大小:
(1)A在最高点的速度为1 m/s;
(2)A在最高点的速度为4 m/s。
9.如图1所示,过山车在轨道上运行,可抽象为图2的模型。倾角为的直轨道、两个半径的竖直圆轨道和倾斜直轨道,分别通过水平轨道、平滑连接,、是两圆轨道最低点。长、长,足够长。质量为的过山车从上静止下滑,经两个圆环轨道后最终停在上。已知过山车与轨道、、的动摩擦因数均为,与圆轨道摩擦不计,。将过山车视为质点。
(1)若过山车恰能通过点,求其运动到点时对轨道的压力;
(2)若过山车恰能通过点,求释放点到的高度;
(3)若保障过山车不脱轨,求释放点到的高度范围。
竖直平面内圆周运动参考答案
1.AD
【详解】
A.游客随摩天轮在竖直平面内做匀速圆周运动,所受向心力的大小不变,方向指向轨迹的圆心,A正确;
B.在转动过程中,做匀速度圆周运动,他与座舱的动能不变,但高度在变化,重力势能在变化,所以机械能在变化,B错误;
D.设转速为n,在最高点时
在最低点时
则
D正确;
C.根据选项D分析可知,在转动过程中,游客对座舱的压力是不断变化的,所以摩擦力不断变化,C错误。
故选AD。
2.BC
【详解】
小球P做圆周运动,经过最高点时的速度设为。若
杆对小球的弹力向上,大小设为,根据向心力公式有
小球从最高点运动到最低点(速度设为),根据动能定理有
即
在最低点杆对小球的弹力大小为,应用向心力公式有
联立可得
结合
可得
若
在最高点杆对小球的弹力向下,大小设为,根据向心力公式有
在最低点有
联立可得
综合上述可知
AD错误,BC正确。
故选BC。
3.D
【详解】
根据
解得
故选D。
4.A
【详解】
AB.当汽车通过凹形路面最低处A时,根据圆周运动的性质可得
又汽车是以恒定的速度运动故可得,A正确,B错误;
CD.当汽车通过凹形路面最低处A时,根据圆周运动的性质可得
又汽车是以恒定的速度运动,故可得,CD错误。
故选A。
5.B
【详解】
A.当在最高点速度为零时,到达最低点的速度最小,对外管壁的压力最小,则由机械能守恒
在最低点设外管壁对小球的支持力为F,由牛顿第二定律
联立解得
由牛顿第三定律得,小球对外管壁的压力最小为5mg,故A错误;
B.小球从静止沿轨道滑落,当滑落高度为时,由机械能守恒
设此时重力沿半径方向的分力为,由几何关系得
此时所需的向心力为
代入数据得
此时重力沿半径方向的分力恰好提供向心力,所以小球与内、外管壁均没有作用力,故B正确;
C.因为管内壁可以给小球支持力,所以小球在最高点的速度可以为零,故C错误;
D.若在最高点速度时,在最高点由牛顿第二定律
最高点到最低点机械能守恒
在最低点时由牛顿第二定律
联立解得
所以当时,小球在最低点与最高点对轨道的压力大小之差为,故D错误。
故选B。
6.D
【详解】
A.如图a,由于汽车做圆周运动,合力指向圆心,因此过拱桥的最高点时所受支持力小于重力,即车对桥面的压力小于车的重力,A错误;
B.如图b,在光滑固定圆锥筒的水平面内做匀速圆周运动的小球,受到重力、弹力,这两个力的合力提供小球做圆周运动的向心力,B错误;
C.如图c,小球在最高点时,若杆的弹力恰好为零,此时
可得
若速度大于,杆对小球的弹力向下,C错误;
D.如图d,设外轨与内轨所在斜面与水平地面夹角为,车轮若对内外轨均无侧向压力,此时
可得速度为
D正确。
故选D。
7.(1)6N(2)60°;0.87m
【详解】
(1)若小球到达点时,管道的上壁对小球有向下的压力,则设在C点的速度为vc,则
从a点到c点,由机械能守恒定律可知
在a点时
解得、两点对小球的弹力大小之差为
(2)若小球在点的速度,在点的速度,根据
可得
小球落地的速度与水平方向的夹角
则
θ=60°
平抛运动的水平位移
8.(1)16N;(2)44N
【详解】
(1)当A在最高点只受重力时,由
得
A在最高点的速度为1 m/s,时,杆对球有支持力,则根据牛顿第二定律
可得
(2) A在最高点的速度为4 m/s时,杆对球有拉力,根据牛顿第二定律
可得
9.(1);(2);(3)
【详解】
(1)对点
对到,由机械能守恒
对点
可得
(2)对从释放点到运动过程:根据动能定理
可得
(3)过山车最终停在上,所以过山车须经过两个圆轨道,则有
