苏科版八下数学第9章 中心对称图形——平行四边形9.3平行四边形(一)学案(无答案)
文档属性
| 名称 | 苏科版八下数学第9章 中心对称图形——平行四边形9.3平行四边形(一)学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 108.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 10:17:16 | ||
图片预览

文档简介
9.3 平行四边形(1)学案
班级:_______________ 姓名:_______________
学习目标:1.理解并掌握平行四边形的概念和性质。
2.会运用平行四边形的性质进行有关边与角的计算和证明。
学习重难点:
重点:平行四边形的概念和性质及应用。
难点:结合平行四边形的性质,进行稍复杂的计算、证明。
学习过程:
一、自主预习,课前导学
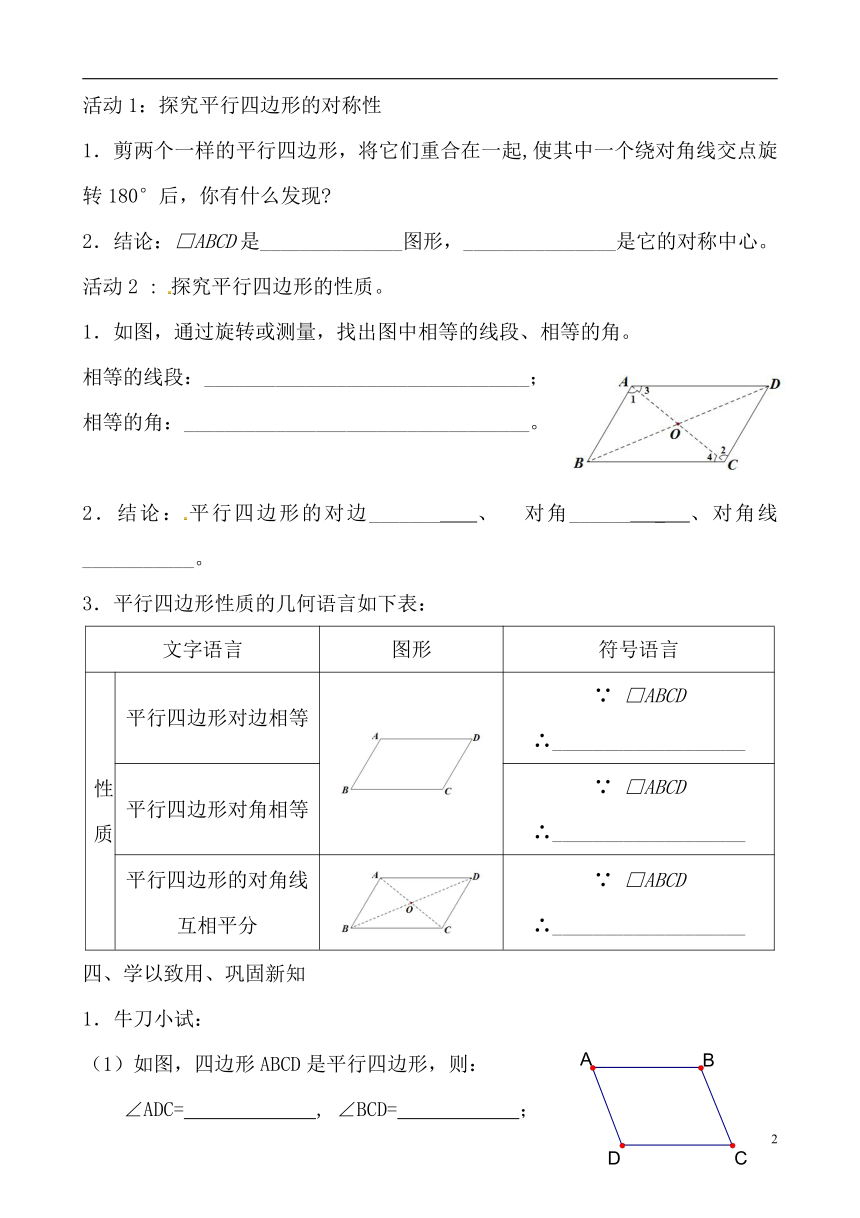
1.如图,在四边形ABCD中,如果AB∥CD,AD∥BC,那么四边形ABCD是 四边形,记作“ ”。
2.平行四边形是 对称图形,对角线的交点是它的 。
3.如图,在□ABCD中,对角线相交于点O,则AB= ,AD= ,∠ABC= ,∠BAD= ,AO= ,BO= 。
二、问题导入、激发兴趣
1.观察下图中的竹篱笆格子和汽车的防护链,想一想它们是什么几何图形的形象?
2.定义:__________________________________的四边形叫做平行四边形。
记作: ,读作: 。
三、自主探究、合作交流
活动1:探究平行四边形的对称性
1.剪两个一样的平行四边形,将它们重合在一起,使其中一个绕对角线交点旋转180°后,你有什么发现
2.结论:□ABCD是______________图形,_______________是它的对称中心。
活动2 : 探究平行四边形的性质。
1.如图,通过旋转或测量,找出图中相等的线段、相等的角。
相等的线段:________________________________;
相等的角:__________________________________。
2.结论:平行四边形的对边_______ 、 对角______ _ 、对角线___________。
3.平行四边形性质的几何语言如下表:
文字语言 图形 符号语言
性质 平行四边形对边相等 ∵ □ABCD∴___________________
平行四边形对角相等 ∵ □ABCD∴___________________
平行四边形的对角线互相平分 ∵ □ABCD∴___________________
四、学以致用、巩固新知
1.牛刀小试:
(1)如图,四边形ABCD是平行四边形,则:
∠ADC= , ∠BCD= ;
边AB= , BC = .
(2)在□ABCD中,如果 ∠A=80°,那么∠B= °,∠C= °,∠D= °。
(3)如果□ABCD的周长为32cm,且AB=5cm,那么BC= cm,CD= cm,
DA= cm。
(4) 如果□ABCD中BC=7 cm,BD=10 cm,AC=6 cm.则△AOD的周长为 。
2.范例研讨:
例:如图,AB∥DE,BC∥EF,CA∥FD.
(1)图中有几个平行四边形,将它们表示出来,并选择其中一个说明理由;
(2)求证:A、B、C分别是△DEF各边的中点。
3.练一练
如图,E、F是□ABCD对角线AC上的两点,BE∥DF.
求证:AF=CE
五、当堂检测
1.下列特征中,平行四边形不一定具是( )。
A 对角互补 B 邻角互补 C 一组对边相等 D 内角和是360°
2.在□ABCD中,已知∠A+ ∠C =140°,那么∠A= ,∠B= ,∠C= ;
3.如图,在□ABCD中,AC=24,BD=40,AD=30,则AO= ,△BOC的周长= ;
4.如图:□ABCD中,AC、BD相交于点O,则图中共有全等三角形( )。
A 1对 B 2对 C 3对 D 4对
5.已知A、B、C三点不在同一条直线上,则以这三点为顶点的平行四边形共有( )。
A 1个 B 2个 C 3个 D 4个
6.平行四边形的两条对角线长分别为8 cm和10 cm,则其边长的范围是( )。
A 2<x<6 B 3<x<9 C 1<x<9 D 2<x<8
7.如图,□ABCD中,BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,
试求:(1)□ABCD的周长;
(2)线段DE的长。
六、拓展延伸
如图:□ABCD的对角线AC、BD相交于点O,直线EF过点O与AD、BC相交于点E、F,请说明:①OE=OF.②若直线EF与DC、BA的延长线相交于F、E,上述结论是否还成立吗?如成立,请说明理由
PAGE
4
班级:_______________ 姓名:_______________
学习目标:1.理解并掌握平行四边形的概念和性质。
2.会运用平行四边形的性质进行有关边与角的计算和证明。
学习重难点:
重点:平行四边形的概念和性质及应用。
难点:结合平行四边形的性质,进行稍复杂的计算、证明。
学习过程:
一、自主预习,课前导学
1.如图,在四边形ABCD中,如果AB∥CD,AD∥BC,那么四边形ABCD是 四边形,记作“ ”。
2.平行四边形是 对称图形,对角线的交点是它的 。
3.如图,在□ABCD中,对角线相交于点O,则AB= ,AD= ,∠ABC= ,∠BAD= ,AO= ,BO= 。
二、问题导入、激发兴趣
1.观察下图中的竹篱笆格子和汽车的防护链,想一想它们是什么几何图形的形象?
2.定义:__________________________________的四边形叫做平行四边形。
记作: ,读作: 。
三、自主探究、合作交流
活动1:探究平行四边形的对称性
1.剪两个一样的平行四边形,将它们重合在一起,使其中一个绕对角线交点旋转180°后,你有什么发现
2.结论:□ABCD是______________图形,_______________是它的对称中心。
活动2 : 探究平行四边形的性质。
1.如图,通过旋转或测量,找出图中相等的线段、相等的角。
相等的线段:________________________________;
相等的角:__________________________________。
2.结论:平行四边形的对边_______ 、 对角______ _ 、对角线___________。
3.平行四边形性质的几何语言如下表:
文字语言 图形 符号语言
性质 平行四边形对边相等 ∵ □ABCD∴___________________
平行四边形对角相等 ∵ □ABCD∴___________________
平行四边形的对角线互相平分 ∵ □ABCD∴___________________
四、学以致用、巩固新知
1.牛刀小试:
(1)如图,四边形ABCD是平行四边形,则:
∠ADC= , ∠BCD= ;
边AB= , BC = .
(2)在□ABCD中,如果 ∠A=80°,那么∠B= °,∠C= °,∠D= °。
(3)如果□ABCD的周长为32cm,且AB=5cm,那么BC= cm,CD= cm,
DA= cm。
(4) 如果□ABCD中BC=7 cm,BD=10 cm,AC=6 cm.则△AOD的周长为 。
2.范例研讨:
例:如图,AB∥DE,BC∥EF,CA∥FD.
(1)图中有几个平行四边形,将它们表示出来,并选择其中一个说明理由;
(2)求证:A、B、C分别是△DEF各边的中点。
3.练一练
如图,E、F是□ABCD对角线AC上的两点,BE∥DF.
求证:AF=CE
五、当堂检测
1.下列特征中,平行四边形不一定具是( )。
A 对角互补 B 邻角互补 C 一组对边相等 D 内角和是360°
2.在□ABCD中,已知∠A+ ∠C =140°,那么∠A= ,∠B= ,∠C= ;
3.如图,在□ABCD中,AC=24,BD=40,AD=30,则AO= ,△BOC的周长= ;
4.如图:□ABCD中,AC、BD相交于点O,则图中共有全等三角形( )。
A 1对 B 2对 C 3对 D 4对
5.已知A、B、C三点不在同一条直线上,则以这三点为顶点的平行四边形共有( )。
A 1个 B 2个 C 3个 D 4个
6.平行四边形的两条对角线长分别为8 cm和10 cm,则其边长的范围是( )。
A 2<x<6 B 3<x<9 C 1<x<9 D 2<x<8
7.如图,□ABCD中,BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,
试求:(1)□ABCD的周长;
(2)线段DE的长。
六、拓展延伸
如图:□ABCD的对角线AC、BD相交于点O,直线EF过点O与AD、BC相交于点E、F,请说明:①OE=OF.②若直线EF与DC、BA的延长线相交于F、E,上述结论是否还成立吗?如成立,请说明理由
PAGE
4
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
