【新人教版】高中物理必修二 5.2运动的合成与分解 课件(17张PPT)
文档属性
| 名称 | 【新人教版】高中物理必修二 5.2运动的合成与分解 课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-29 16:16:26 | ||
图片预览




文档简介
(共17张PPT)
5.2 运动的合成与分解
新人教版 必修二
1.会根据研究问题的需要建立合适的平面直角坐标系,并用函数描述直线运动。
2.理解合运动与分运动的概念,能对简单平面运动进行合成与分解。
3.通过运动的合成与分解,初步体会把复杂运动分解为简单运动的物理思想,并能用这个思想解决类似的简单问题。
学习目标
引入
若人在河中始终保持头朝正前方游向对岸,你认为他会在对岸的正前方到达,还是会偏上游或下游?为什么?
A B C
v
过河
一、一个平面运动的实例
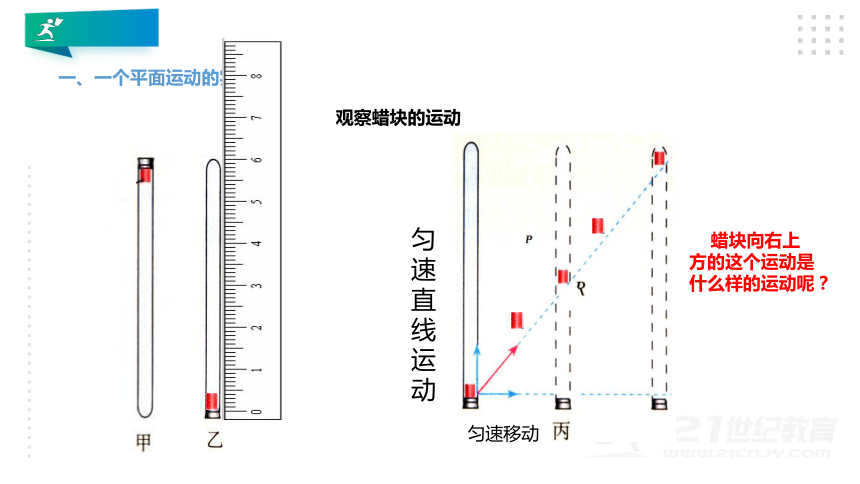
观察蜡块的运动
匀速直线运动
匀速直线运动
匀速移动
蜡块向右上方的这个运动是什么样的运动呢?
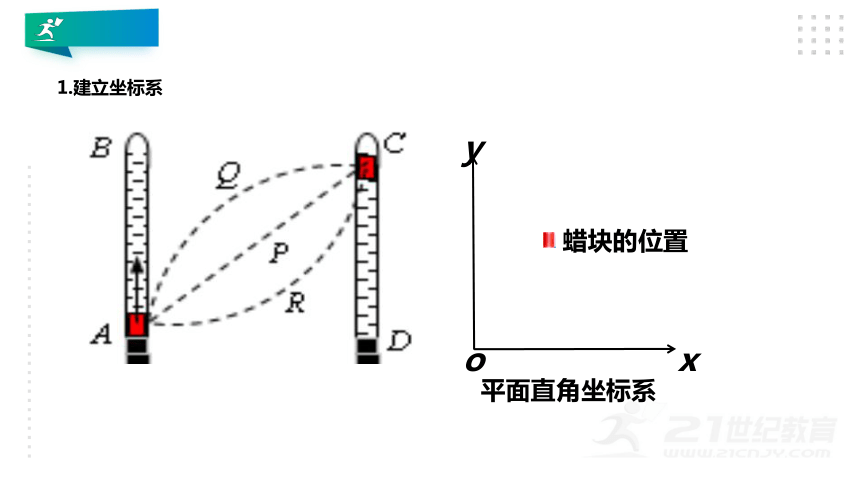
1.建立坐标系
平面直角坐标系
o
x
y
蜡块的位置
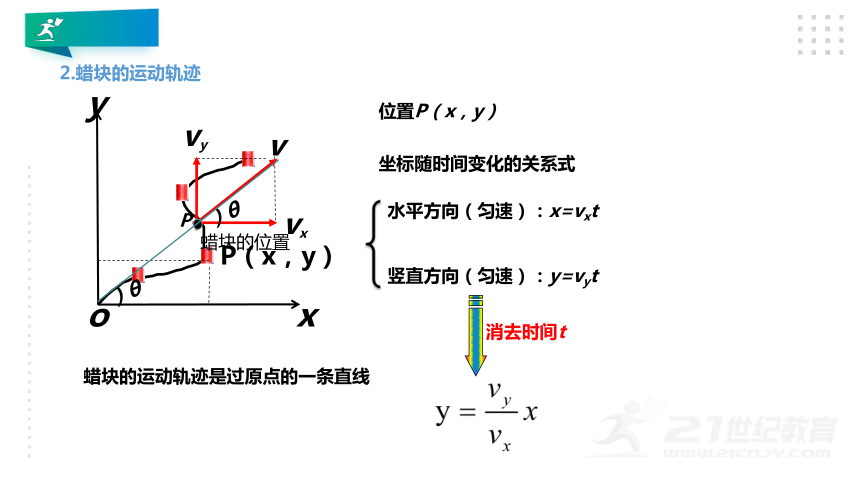
2.蜡块的运动轨迹
o
x
y
坐标随时间变化的关系式
vx
vy
v
)θ
P
蜡块的位置
位置P(x,y)
P(x,y)
水平方向(匀速):x=vxt
竖直方向(匀速):y=vyt
消去时间t
)θ
蜡块的运动轨迹是过原点的一条直线
速度的方向:
3.蜡块运动的速度:
二、运动的合成与分解
合运动
分运动
分运动
2.物体同时参与合成的运动叫分运动
1.物体实际的运动叫合运动
A B C
v
过河
O
分运动
OB,即游泳
BA,即水流
合运动:OA,即实际运动
特征:
等效性、同一性、等时性、独立性
分运动
合运动
运动的合成
运动的分解
遵循平行四边形定则
三角形定则
分速度
分加速度
合速度
合加速度
合位移
分位移
唯一
多种可能
合运动
选择容易计算的分解方式
例 某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是0.15 m,自动扶梯平面的夹角为30°,自动扶梯前进的速度是0.76 m/s。有甲、乙两位顾客,分别动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上秒上两个台阶的速度匀速上楼。哪位顾客先到达楼上?如果该楼层高4.56m,甲上楼用了多少时间?
分析:甲、乙两位顾客在竖直方向上的位移相等,可考虑比较他们在竖直方向的分速度。由竖直方向的位移和竖直方向的速度,可求出上楼所用的时间。
解 甲在竖直方向的速度
v甲
v甲y
v甲x
)θ
v甲y=v甲sinθ=0.76×sin30 =0.38m/s
乙在竖直方向的速度
本课小结
1.物体实际的运动叫合运动
2.物体同时参与合成的运动叫分运动
3.特征:
等效性
、同一性
、等时性
、独立性
4.遵循平行四边形定则和三角形定则
5.合成运动性质的判断:看合加速度a与合速度v是否共线。
当堂检测
1. 如图甲所示,竖直放置、两端封闭的玻璃管中注满清水,内有一个能在水中以0.3 m/s的速度匀速上浮的红蜡块。若红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动的方向与水平方向的夹角为37°,则:(sin 37°=0.6,cos 37°=0.8)
(1)根据题意可知玻璃管水平方向的移动速度为 m/s。
(2)如图乙所示,若红蜡块从A点匀速上浮的同时,使玻璃管水平向右做匀加速直线运动,则红蜡块实际运动的轨迹是图中的 。
A.直线P B.曲线Q C.曲线R D.无法确定
0.4
甲
乙
B
2. 直角坐标系xOy在水平面内,一物体的运动规律是x=3t2 m,y=4t2 m(t的单位为s),则下列说法中正确的是 ( )
①物体在x和y方向上都是做初速度为零的匀加速运动
②物体的合运动是初速度为零、加速度为5 m/s2的匀加速直线运动
③物体的合运动是初速度为零、加速度为10 m/s2的匀加速直线运动
④物体的合运动是加速度为5 m/s2的曲线运动
A.①② B.①③ C.②③ D.②④
B
解析:结合匀变速直线运动位移表达式x=v0t+知,
在x方向:x=3t2 m,则ax=6 m/s2,v0x=0,
在y方向:y=4t2 m,则ay=8 m/s2,v0y=0,
3. 质量m=2 kg的物体在光滑水平面上运动,其两个相互垂直的x、y方向上的分速度和随时间变化的图线如图所示,求:
(1)物体的初速度大小;
(2)t1=8 s时物体的速度大小;
(3)t2=4 s时物体的位移大小。
【解】(1)物体沿x方向上的初速度v0x=3 m/s,沿y方向上的初速度v0y=0,所以其合初速度为v0=3 m/s;
(2)t1=8 s时物体沿x方向上的速度v8x=3 m/s,沿y方向上的速度v8y=4 m/s,
此时物体的速度
v8= m/s =5 m/s;
(3)t2=4 s时物体在x方向上的位移,x=4×3 m=12 m;
在y方向上的位移y=×4×2m =4 m,则总位移s=m 。
https://www.21cnjy.com/help/help_extract.php
5.2 运动的合成与分解
新人教版 必修二
1.会根据研究问题的需要建立合适的平面直角坐标系,并用函数描述直线运动。
2.理解合运动与分运动的概念,能对简单平面运动进行合成与分解。
3.通过运动的合成与分解,初步体会把复杂运动分解为简单运动的物理思想,并能用这个思想解决类似的简单问题。
学习目标
引入
若人在河中始终保持头朝正前方游向对岸,你认为他会在对岸的正前方到达,还是会偏上游或下游?为什么?
A B C
v
过河
一、一个平面运动的实例
观察蜡块的运动
匀速直线运动
匀速直线运动
匀速移动
蜡块向右上方的这个运动是什么样的运动呢?
1.建立坐标系
平面直角坐标系
o
x
y
蜡块的位置
2.蜡块的运动轨迹
o
x
y
坐标随时间变化的关系式
vx
vy
v
)θ
P
蜡块的位置
位置P(x,y)
P(x,y)
水平方向(匀速):x=vxt
竖直方向(匀速):y=vyt
消去时间t
)θ
蜡块的运动轨迹是过原点的一条直线
速度的方向:
3.蜡块运动的速度:
二、运动的合成与分解
合运动
分运动
分运动
2.物体同时参与合成的运动叫分运动
1.物体实际的运动叫合运动
A B C
v
过河
O
分运动
OB,即游泳
BA,即水流
合运动:OA,即实际运动
特征:
等效性、同一性、等时性、独立性
分运动
合运动
运动的合成
运动的分解
遵循平行四边形定则
三角形定则
分速度
分加速度
合速度
合加速度
合位移
分位移
唯一
多种可能
合运动
选择容易计算的分解方式
例 某商场设有步行楼梯和自动扶梯,步行楼梯每级的高度是0.15 m,自动扶梯平面的夹角为30°,自动扶梯前进的速度是0.76 m/s。有甲、乙两位顾客,分别动扶梯和步行楼梯的起点同时上楼,甲在自动扶梯上站立不动,乙在步行楼梯上秒上两个台阶的速度匀速上楼。哪位顾客先到达楼上?如果该楼层高4.56m,甲上楼用了多少时间?
分析:甲、乙两位顾客在竖直方向上的位移相等,可考虑比较他们在竖直方向的分速度。由竖直方向的位移和竖直方向的速度,可求出上楼所用的时间。
解 甲在竖直方向的速度
v甲
v甲y
v甲x
)θ
v甲y=v甲sinθ=0.76×sin30 =0.38m/s
乙在竖直方向的速度
本课小结
1.物体实际的运动叫合运动
2.物体同时参与合成的运动叫分运动
3.特征:
等效性
、同一性
、等时性
、独立性
4.遵循平行四边形定则和三角形定则
5.合成运动性质的判断:看合加速度a与合速度v是否共线。
当堂检测
1. 如图甲所示,竖直放置、两端封闭的玻璃管中注满清水,内有一个能在水中以0.3 m/s的速度匀速上浮的红蜡块。若红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管水平匀速向右运动,测得红蜡块实际运动的方向与水平方向的夹角为37°,则:(sin 37°=0.6,cos 37°=0.8)
(1)根据题意可知玻璃管水平方向的移动速度为 m/s。
(2)如图乙所示,若红蜡块从A点匀速上浮的同时,使玻璃管水平向右做匀加速直线运动,则红蜡块实际运动的轨迹是图中的 。
A.直线P B.曲线Q C.曲线R D.无法确定
0.4
甲
乙
B
2. 直角坐标系xOy在水平面内,一物体的运动规律是x=3t2 m,y=4t2 m(t的单位为s),则下列说法中正确的是 ( )
①物体在x和y方向上都是做初速度为零的匀加速运动
②物体的合运动是初速度为零、加速度为5 m/s2的匀加速直线运动
③物体的合运动是初速度为零、加速度为10 m/s2的匀加速直线运动
④物体的合运动是加速度为5 m/s2的曲线运动
A.①② B.①③ C.②③ D.②④
B
解析:结合匀变速直线运动位移表达式x=v0t+知,
在x方向:x=3t2 m,则ax=6 m/s2,v0x=0,
在y方向:y=4t2 m,则ay=8 m/s2,v0y=0,
3. 质量m=2 kg的物体在光滑水平面上运动,其两个相互垂直的x、y方向上的分速度和随时间变化的图线如图所示,求:
(1)物体的初速度大小;
(2)t1=8 s时物体的速度大小;
(3)t2=4 s时物体的位移大小。
【解】(1)物体沿x方向上的初速度v0x=3 m/s,沿y方向上的初速度v0y=0,所以其合初速度为v0=3 m/s;
(2)t1=8 s时物体沿x方向上的速度v8x=3 m/s,沿y方向上的速度v8y=4 m/s,
此时物体的速度
v8= m/s =5 m/s;
(3)t2=4 s时物体在x方向上的位移,x=4×3 m=12 m;
在y方向上的位移y=×4×2m =4 m,则总位移s=m 。
https://www.21cnjy.com/help/help_extract.php
