2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列前n项和公式(一)课件(20张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列前n项和公式(一)课件(20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 38.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-29 20:33:07 | ||
图片预览









文档简介
(共39张PPT)
等差数列的
前项和公式
Mathematics
(1)在等差数列中
课前练习
解答
解答
解答
(2)在等差数列中
(3)在等差数列中
“数学王子”高斯的开挂人生
据说,二百多年前,高斯的算术老师提出了下面问题:1+2+3+...+100=
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案:
情境导入
新知探究
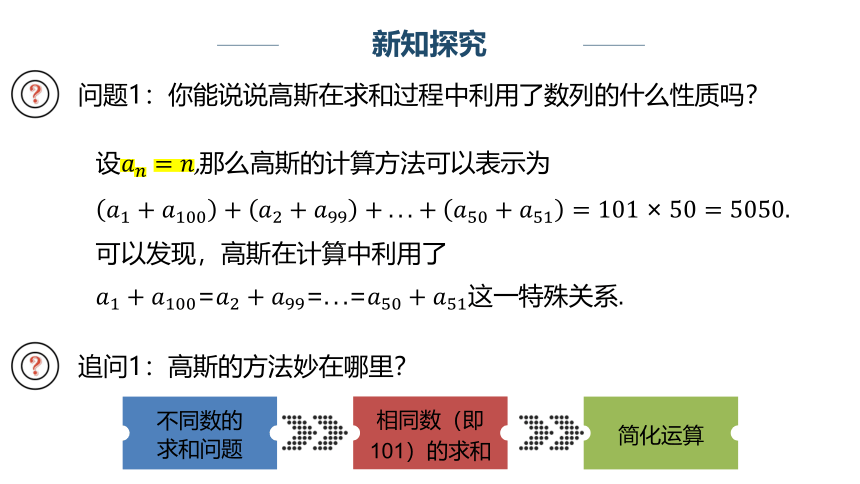
问题1:你能说说高斯在求和过程中利用了数列的什么性质吗?
,那么高斯的计算方法可以表示为
可以发现,高斯在计算中利用了
===这一特殊关系.
追问1:高斯的方法妙在哪里?
相同数(即101)的求和
简化运算
不同数的
求和问题
新知探究
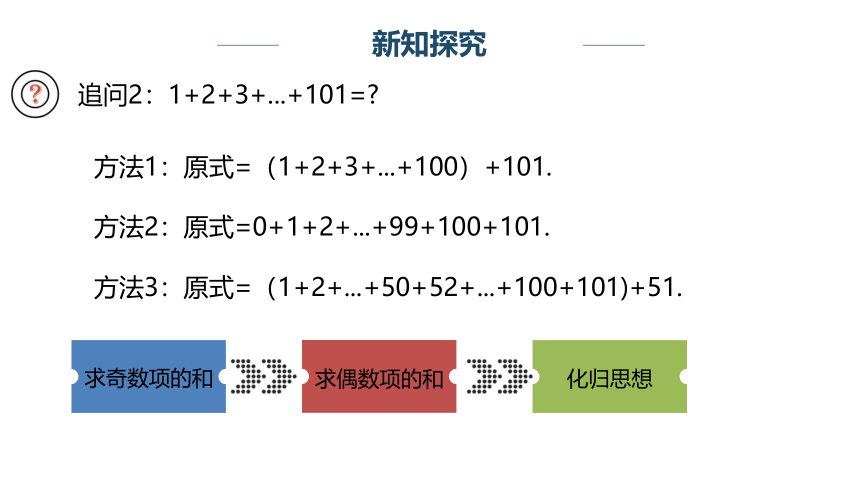
追问2:1+2+3+...+101=
方法1:原式=(1+2+3+...+100)+101.
方法2:原式=0+1+2+...+99+100+101.
方法3:原式=(1+2+...+50+52+...+100+101)+51.
求偶数项的和
化归思想
求奇数项的和
新知探究
问题2:1+2+3+...+n=
,
当n为偶数时,有
当n为奇数时,有
个
个
新知探究
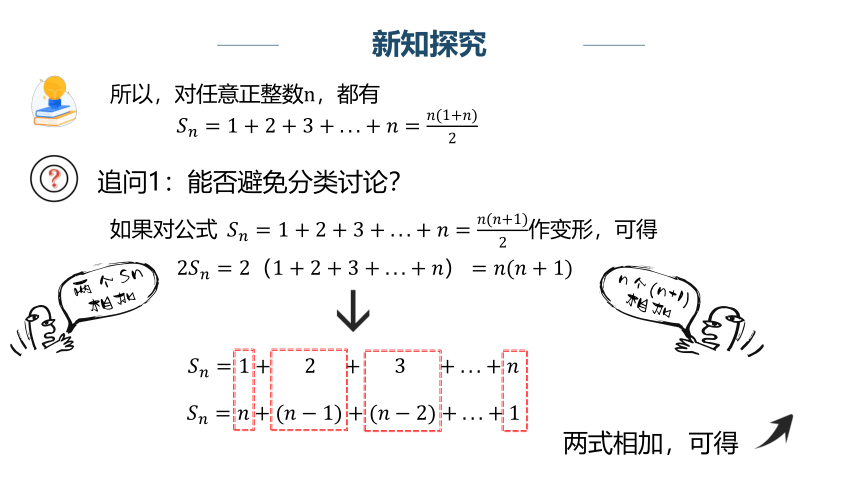
所以,对任意正整数n,都有
追问1:能否避免分类讨论?
如果对公式 作变形,可得
2
两个Sn相加
n个(n+1)相加
两式相加,可得
新知探究
个
所以
倒序相加法
追问2:倒序相加法能够推广到求等差数列的前项和吗?
新知探究
问题3:设数列 {an }为等差数列 ,
Sn =a1 +a2 + a3 +…+ an-1 +an =?
Sn =a1 + a2 + a3 +…+ an-1 + an
Sn =an +an-1 + an-2 +…+ a2 + a1
个
等差数列 {an }的求和公式
新知探究
追问1:把等差数列的通项公式代入公式(1),可以得到什么?
(2)
追问2:不从公式(1)出发,你能用其他方法得到公式(2)吗?
Sn =a1 +a2 + a3 +…+ an-1 +an
+
追问2:不从公式(1)出发,你能用其他方法得到公式(2)吗?
数学应用
练习:计算
(1)2+4+6+...+2n
(2)1+3+7+...+(2n+1)
(1)若a1=7,a50=101,求S50;
数学例题
(3)若a1=,d= - , Sn = -5,求n.
(2)若a1=2,a2=,求S10;
(4)a1,d
例1 已知数列{an}是等差数列.
2700
12
解:
解得
古今数学
今有女子不善织布,逐日所织的布以同数递减,初日织五尺,末一日织一尺,计织三十日,问共织几何?
原书解法:
并初、末日织布数,半之,余以乘织讫日数,即得.
———《张邱建算经》
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
好好学习·天天向上
Mathematics
TEACHING
Mathematics Teaching
等差数列的
前项和公式
Mathematics
(1)在等差数列中
课前练习
解答
解答
解答
(2)在等差数列中
(3)在等差数列中
“数学王子”高斯的开挂人生
据说,二百多年前,高斯的算术老师提出了下面问题:1+2+3+...+100=
当其他同学忙于把100个数逐项相加时,10岁的高斯却用下面的方法迅速算出了正确答案:
情境导入
新知探究
问题1:你能说说高斯在求和过程中利用了数列的什么性质吗?
,那么高斯的计算方法可以表示为
可以发现,高斯在计算中利用了
===这一特殊关系.
追问1:高斯的方法妙在哪里?
相同数(即101)的求和
简化运算
不同数的
求和问题
新知探究
追问2:1+2+3+...+101=
方法1:原式=(1+2+3+...+100)+101.
方法2:原式=0+1+2+...+99+100+101.
方法3:原式=(1+2+...+50+52+...+100+101)+51.
求偶数项的和
化归思想
求奇数项的和
新知探究
问题2:1+2+3+...+n=
,
当n为偶数时,有
当n为奇数时,有
个
个
新知探究
所以,对任意正整数n,都有
追问1:能否避免分类讨论?
如果对公式 作变形,可得
2
两个Sn相加
n个(n+1)相加
两式相加,可得
新知探究
个
所以
倒序相加法
追问2:倒序相加法能够推广到求等差数列的前项和吗?
新知探究
问题3:设数列 {an }为等差数列 ,
Sn =a1 +a2 + a3 +…+ an-1 +an =?
Sn =a1 + a2 + a3 +…+ an-1 + an
Sn =an +an-1 + an-2 +…+ a2 + a1
个
等差数列 {an }的求和公式
新知探究
追问1:把等差数列的通项公式代入公式(1),可以得到什么?
(2)
追问2:不从公式(1)出发,你能用其他方法得到公式(2)吗?
Sn =a1 +a2 + a3 +…+ an-1 +an
+
追问2:不从公式(1)出发,你能用其他方法得到公式(2)吗?
数学应用
练习:计算
(1)2+4+6+...+2n
(2)1+3+7+...+(2n+1)
(1)若a1=7,a50=101,求S50;
数学例题
(3)若a1=,d= - , Sn = -5,求n.
(2)若a1=2,a2=,求S10;
(4)a1,d
例1 已知数列{an}是等差数列.
2700
12
解:
解得
古今数学
今有女子不善织布,逐日所织的布以同数递减,初日织五尺,末一日织一尺,计织三十日,问共织几何?
原书解法:
并初、末日织布数,半之,余以乘织讫日数,即得.
———《张邱建算经》
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
高考领航
好好学习·天天向上
Mathematics
TEACHING
Mathematics Teaching
