直线与直线的位置关系
图片预览







文档简介
课件40张PPT。2.1.2空间中直线与
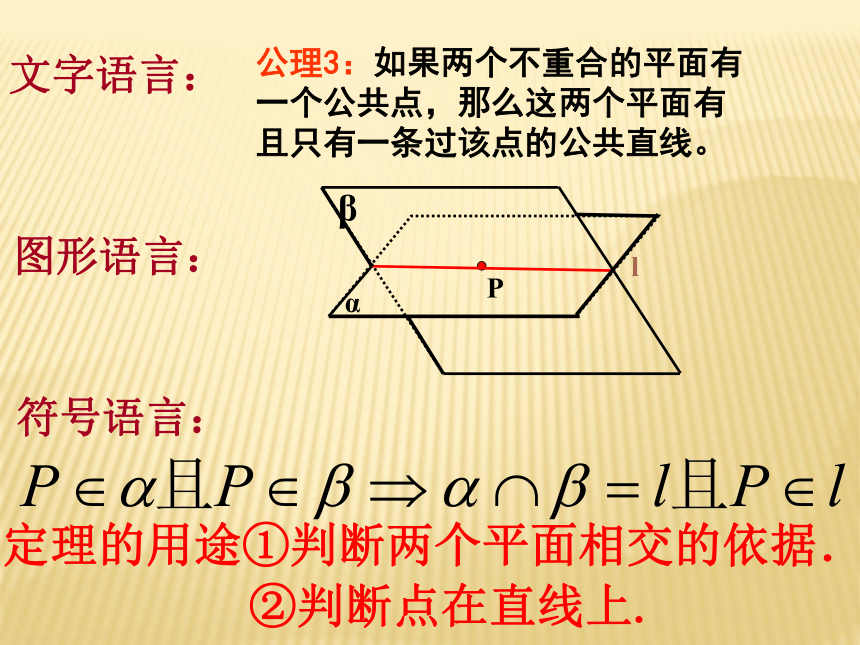
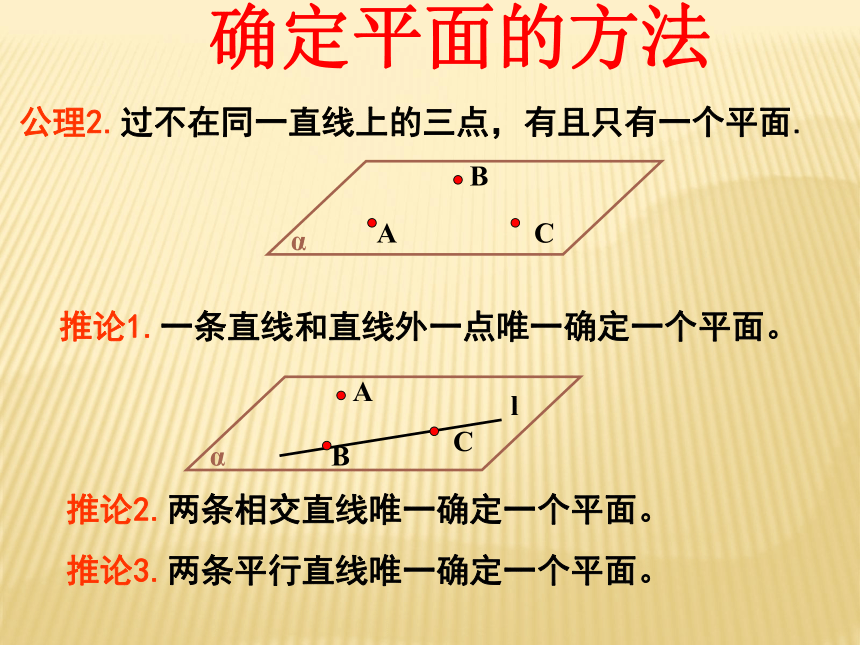
直线之间的位置关系公理1:如果一条直线上两点在一个平面内,那么这条直线在此平面内(即这条直线上的所有的点都在这个平面内)。文字语言:图形语言:符号语言:定理的用途:判定直线是否在平面内.文字语言:图形语言:符号语言:公理2:过不在同一直线上的三点,有且只有一个平面.定理的用途:确定平面的主要依据.文字语言:图形语言:符号语言:公理3:如果两个不重合的平面有一个公共点,那么这两个平面有且只有一条过该点的公共直线。定理的用途①判断两个平面相交的依据.②判断点在直线上.推论1.一条直线和直线外一点唯一确定一个平面。推论2.两条相交直线唯一确定一个平面。推论3.两条平行直线唯一确定一个平面。公理2.过不在同一直线上的三点,有且只有一个平面.确定平面的方法判断下列命题对错:
1、如果一条直线上有一个点在一个平面上,则这条直线上的所有点都在这个平面内。( )
2、将书的一角接触课桌面,这时书所在平面和课桌所在平面只有一个公共点。 ( )
3、四个点中如果有三个点在同一条直线上,那么这四个点必在同一个平面内。 ( )
4、一条直线和一个点可以确定一个平面。( )
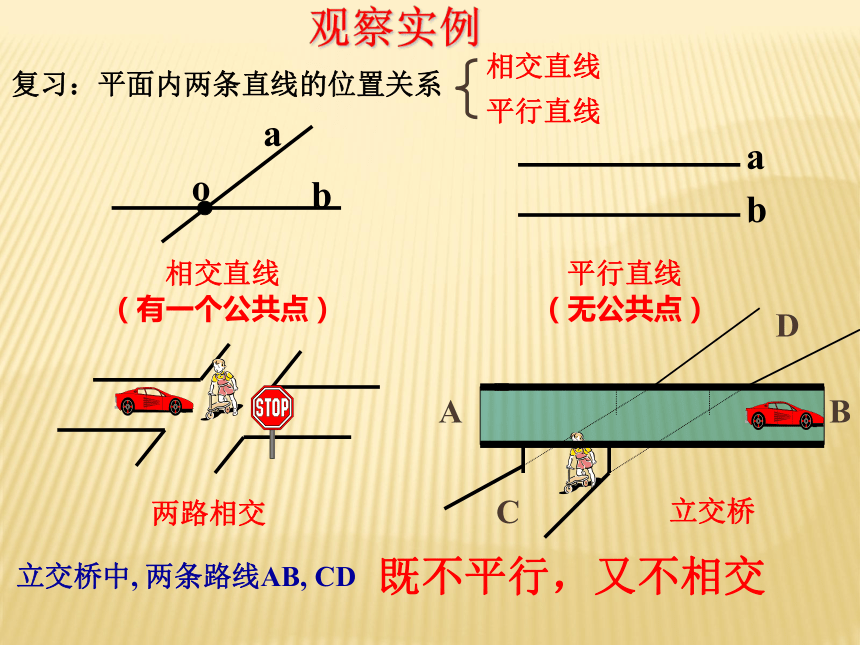
5、如果一条直线和另两条直线都相交,那么这三条直线可以确定一个平面。 ( )?????温故知新温故知新复习:平面内两条直线的位置关系相交直线
(有一个公共点)平行直线
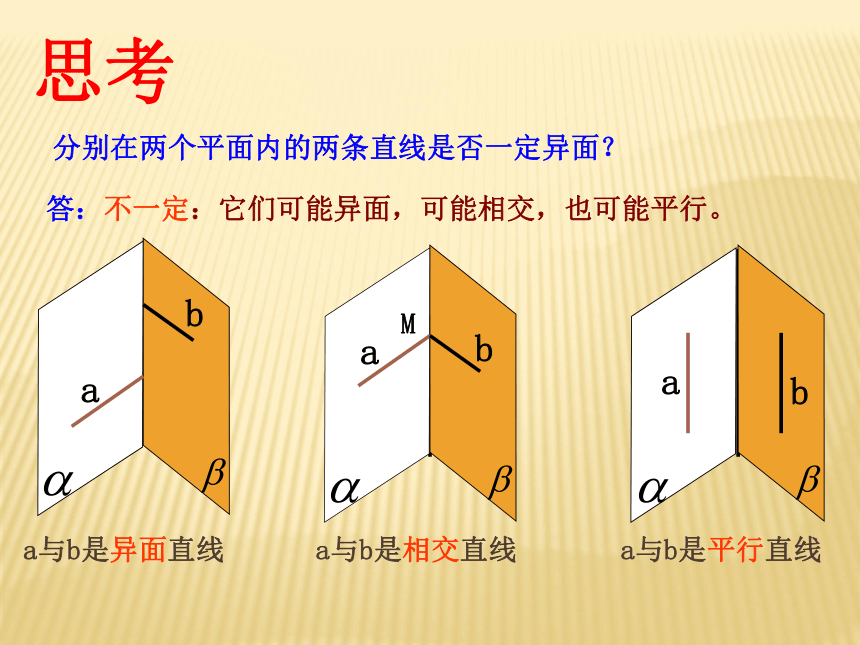
(无公共点)两路相交立交桥立交桥中, 两条路线AB, CD既不平行,又不相交观察实例 不同在任何一个平面内的两条直线叫做异面直线。没有只有一个没有共面不共面共面1.异面直线的定义a与b是相交直线a与b是平行直线a与b是异面直线答:不一定:它们可能异面,可能相交,也可能平行。 分别在两个平面内的两条直线是否一定异面?思考练习判断:直线m和l是异面直线吗?(2) ,则 a与b是异面直线(3)a,b不同在平面α 内,则a与b异面空间直线与直线之间的位置关系 按平面基本性质分同在一个平面内相交直线平行直线 不同在任何一个平面内:异面直线 有一个公共点: 按公共点个数分相交直线无 公 共 点平行直线异面直线空间直线与直线之间的位置关系2.异面直线的画法说明: 画异面直线时 , 为了体现
它们不共面的特点。常借
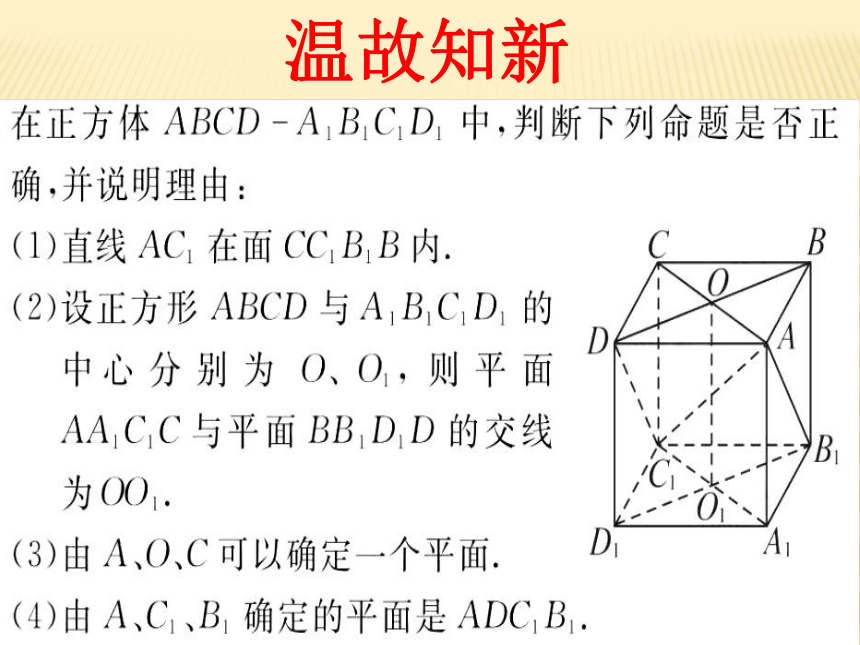
助一个或两个平面来衬托.如图:(1)(3)(2)3、异面直线的判定方法:(1)定义法:由定义判定两直线不可能在同一平面内.(借助反证法)(2)判定定理:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线(1)在如图所示的正方体中,指出哪些
棱所在的直线与直线BA1是异面直线?ABCDA1B1D1C1⑵已知M、N分别是长方体的棱C1D1与CC1
上的点,那么MN与AB所在的直线相交吗?ABCDA1B1D1C1MN公理4:平行于同一条直线的两条直线互相平行注:
1、直线a,b,c 两两平行,可记为a // b // c 2、公理4所表述的性质,叫做空间平行线的传递性3、证明空间两直线平行 的方法:
(1) 定义法:一要证两直线在同一平面内;二要证两直线没有公共点(反证法)
(2) 公理法平行公理例2:如图,空间四边行ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.D变式:如果再加上条件AC=BD,那么四边形EFGH是什么图形? 立体问题平面化是解立体几何时最主要、最常用的一种方法。四边形ABCD是空间四边形,E、H分别是AB,AD的中点 ,F、G分别是CB,CD上的点,且
求证:四边形EFGH是梯形练习等角定理1:如果一个角的两边和另一个角的两边分别对应平行,那么这两个角相等或互补等角定理2:如果一个角的两边和另一个角的两边分别平行且方向相同,那么这两个角相等等角定理定义:直线a、b为异面直线,经过空间任一点O,分别引a′∥a,b′∥b,则相交直线a′,b′所成的锐角(或直角)叫做两条异面直线a、b所成的角(或夹角)4、两条异面直线所成的角注1:异面直线a、b所成角,只与a、b的相互位置有关,而与点O位置无关注2:一般常把点O取在直线a或b上注3:异面直线所成角的取值范围:如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作 a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角。?任选若两条异面直线所成角为90°,则称它们互相垂直。异面直线a与b垂直也记作a⊥b异面直线所成角θ的取值范围: 平移4、两条异面直线所成的角一作(找)二证三求例1、如图表示一个正方体(1)图中哪些棱所在的直线与直线BA1成异面直线(2)求直线BA1与CC1的夹角的度数(3)哪些棱所在的直线与直线AA1垂直典例剖析例2、如图,在长方体中,已知AA1=AD=a,
AB= a,求AB1与BC1所成的角的余弦值CBADA1B1C1D1典例剖析aa空间两条直线的位置关系:相交、平行、异面⑴空间两条直线的位置关系归纳为: 如图,已知长方体ABCD-EFGH中, AB = , AD = , AE = 2
(1)求BC 和EG 所成的角是多少度?
(2)求AE 和BG 所成的角是多少度?解答:练习小结典例赏析练一练典例赏析练一练练一练作业1.阅读教材第40页至第47页2.教材第51页A组第4,5,6题3.红对勾第7课时
直线之间的位置关系公理1:如果一条直线上两点在一个平面内,那么这条直线在此平面内(即这条直线上的所有的点都在这个平面内)。文字语言:图形语言:符号语言:定理的用途:判定直线是否在平面内.文字语言:图形语言:符号语言:公理2:过不在同一直线上的三点,有且只有一个平面.定理的用途:确定平面的主要依据.文字语言:图形语言:符号语言:公理3:如果两个不重合的平面有一个公共点,那么这两个平面有且只有一条过该点的公共直线。定理的用途①判断两个平面相交的依据.②判断点在直线上.推论1.一条直线和直线外一点唯一确定一个平面。推论2.两条相交直线唯一确定一个平面。推论3.两条平行直线唯一确定一个平面。公理2.过不在同一直线上的三点,有且只有一个平面.确定平面的方法判断下列命题对错:
1、如果一条直线上有一个点在一个平面上,则这条直线上的所有点都在这个平面内。( )
2、将书的一角接触课桌面,这时书所在平面和课桌所在平面只有一个公共点。 ( )
3、四个点中如果有三个点在同一条直线上,那么这四个点必在同一个平面内。 ( )
4、一条直线和一个点可以确定一个平面。( )
5、如果一条直线和另两条直线都相交,那么这三条直线可以确定一个平面。 ( )?????温故知新温故知新复习:平面内两条直线的位置关系相交直线
(有一个公共点)平行直线
(无公共点)两路相交立交桥立交桥中, 两条路线AB, CD既不平行,又不相交观察实例 不同在任何一个平面内的两条直线叫做异面直线。没有只有一个没有共面不共面共面1.异面直线的定义a与b是相交直线a与b是平行直线a与b是异面直线答:不一定:它们可能异面,可能相交,也可能平行。 分别在两个平面内的两条直线是否一定异面?思考练习判断:直线m和l是异面直线吗?(2) ,则 a与b是异面直线(3)a,b不同在平面α 内,则a与b异面空间直线与直线之间的位置关系 按平面基本性质分同在一个平面内相交直线平行直线 不同在任何一个平面内:异面直线 有一个公共点: 按公共点个数分相交直线无 公 共 点平行直线异面直线空间直线与直线之间的位置关系2.异面直线的画法说明: 画异面直线时 , 为了体现
它们不共面的特点。常借
助一个或两个平面来衬托.如图:(1)(3)(2)3、异面直线的判定方法:(1)定义法:由定义判定两直线不可能在同一平面内.(借助反证法)(2)判定定理:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线(1)在如图所示的正方体中,指出哪些
棱所在的直线与直线BA1是异面直线?ABCDA1B1D1C1⑵已知M、N分别是长方体的棱C1D1与CC1
上的点,那么MN与AB所在的直线相交吗?ABCDA1B1D1C1MN公理4:平行于同一条直线的两条直线互相平行注:
1、直线a,b,c 两两平行,可记为a // b // c 2、公理4所表述的性质,叫做空间平行线的传递性3、证明空间两直线平行 的方法:
(1) 定义法:一要证两直线在同一平面内;二要证两直线没有公共点(反证法)
(2) 公理法平行公理例2:如图,空间四边行ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.D变式:如果再加上条件AC=BD,那么四边形EFGH是什么图形? 立体问题平面化是解立体几何时最主要、最常用的一种方法。四边形ABCD是空间四边形,E、H分别是AB,AD的中点 ,F、G分别是CB,CD上的点,且
求证:四边形EFGH是梯形练习等角定理1:如果一个角的两边和另一个角的两边分别对应平行,那么这两个角相等或互补等角定理2:如果一个角的两边和另一个角的两边分别平行且方向相同,那么这两个角相等等角定理定义:直线a、b为异面直线,经过空间任一点O,分别引a′∥a,b′∥b,则相交直线a′,b′所成的锐角(或直角)叫做两条异面直线a、b所成的角(或夹角)4、两条异面直线所成的角注1:异面直线a、b所成角,只与a、b的相互位置有关,而与点O位置无关注2:一般常把点O取在直线a或b上注3:异面直线所成角的取值范围:如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作 a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角。?任选若两条异面直线所成角为90°,则称它们互相垂直。异面直线a与b垂直也记作a⊥b异面直线所成角θ的取值范围: 平移4、两条异面直线所成的角一作(找)二证三求例1、如图表示一个正方体(1)图中哪些棱所在的直线与直线BA1成异面直线(2)求直线BA1与CC1的夹角的度数(3)哪些棱所在的直线与直线AA1垂直典例剖析例2、如图,在长方体中,已知AA1=AD=a,
AB= a,求AB1与BC1所成的角的余弦值CBADA1B1C1D1典例剖析aa空间两条直线的位置关系:相交、平行、异面⑴空间两条直线的位置关系归纳为: 如图,已知长方体ABCD-EFGH中, AB = , AD = , AE = 2
(1)求BC 和EG 所成的角是多少度?
(2)求AE 和BG 所成的角是多少度?解答:练习小结典例赏析练一练典例赏析练一练练一练作业1.阅读教材第40页至第47页2.教材第51页A组第4,5,6题3.红对勾第7课时
