2021-2022学年苏科版数学八年级上册 第6章一次函数单元达标复习题 (word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级上册 第6章一次函数单元达标复习题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 95.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 19:04:21 | ||
图片预览



文档简介
第6章一次函数单元达标复习题
一、选择题:
1.在以x为自变量、y为函数的关系式y=2πx中,常量为( )
A.2 B.π C.2π D.πx
2.在函数y=中,自变量x的取值范围是( )
A.x≠2 B.x≥2 C.x≤2 D.x>2
3.若正比例函数y=(2﹣k)x的图象经过第二、四象限,则k的取值范围是( )
A.k<﹣2 B.k<2 C.k>﹣2 D.k>2
4.在下面的两种相关联的量,成比例的是( )
A.和是15的两个加数 B.一个人的年龄和身高
C.长方形的宽一定,周长和长 D.单价一定,买乒乓球的个数和钱数
5.将直线y=2x﹣3向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( )
A.y=2x﹣4 B.y=2x+4 C.y=2x+2 D.y=2x﹣2
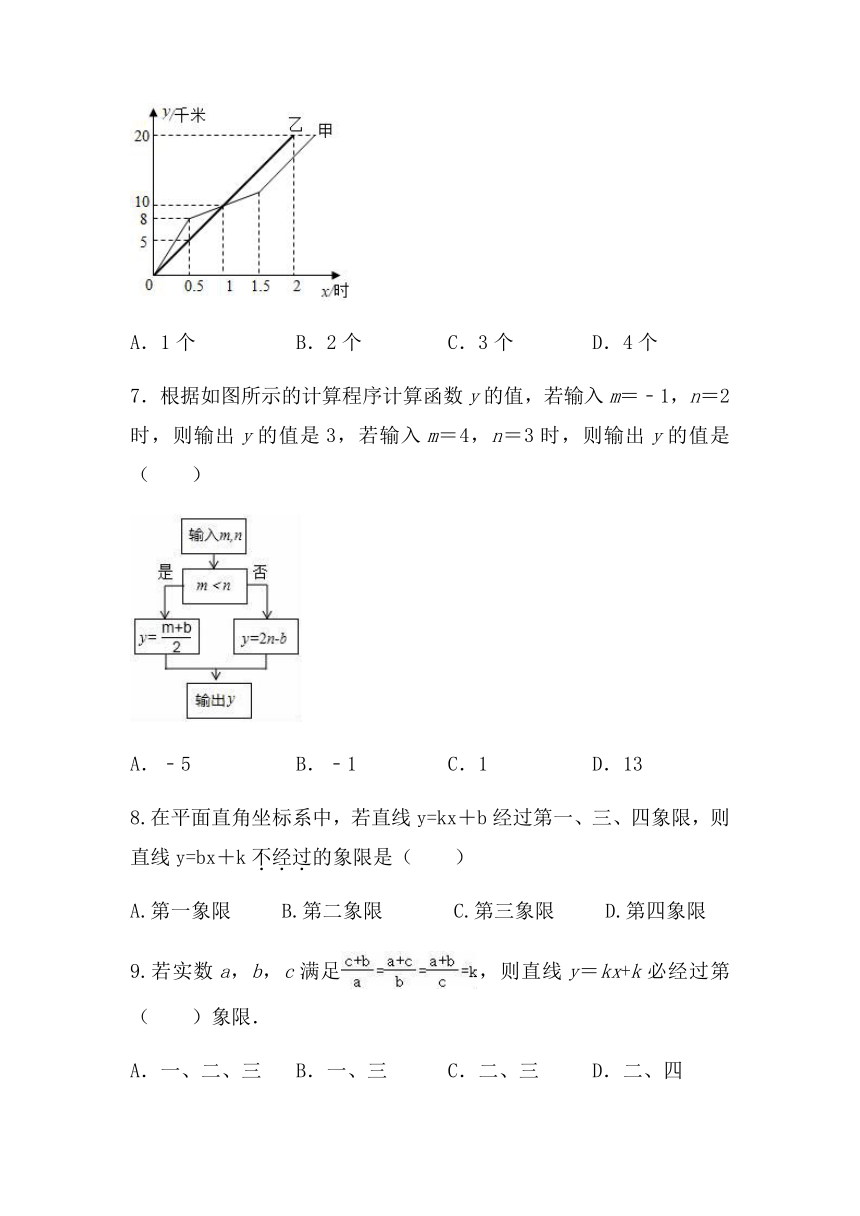
6.在全民健身越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:①前半小时甲选手的速度为8千米/时;②第1小时两人都跑了10千米;③甲比乙先到达终点;④甲选手的速度一直比乙慢.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
7.根据如图所示的计算程序计算函数y的值,若输入m=﹣1,n=2时,则输出y的值是3,若输入m=4,n=3时,则输出y的值是( )
A.﹣5 B.﹣1 C.1 D.13
8.在平面直角坐标系中,若直线y=kx+b经过第一、三、四象限,则直线y=bx+k不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.若实数a,b,c满足,则直线y=kx+k必经过第( )象限.
A.一、二、三 B.一、三 C.二、三 D.二、四
二、填空题:
10.如果正比例函数y=kx的图象经过第一、三象限,那么y的值随着x的值增大而 .(填“增大”或“减小”)
11.已知一次函数y=2x+b的图象经过点A(2,y1)和B(﹣1,y2),则y1 y2(填“>”、“<”或“=”).
12.若函数y=2x+(1﹣m)是正比例函数,则m的值是 .
13.有下列关于变量x,y的表达式:①y=x;②y=2x2;③|y|=x;④y2=﹣x.其中,表示y是x的函数的是 (填序号).
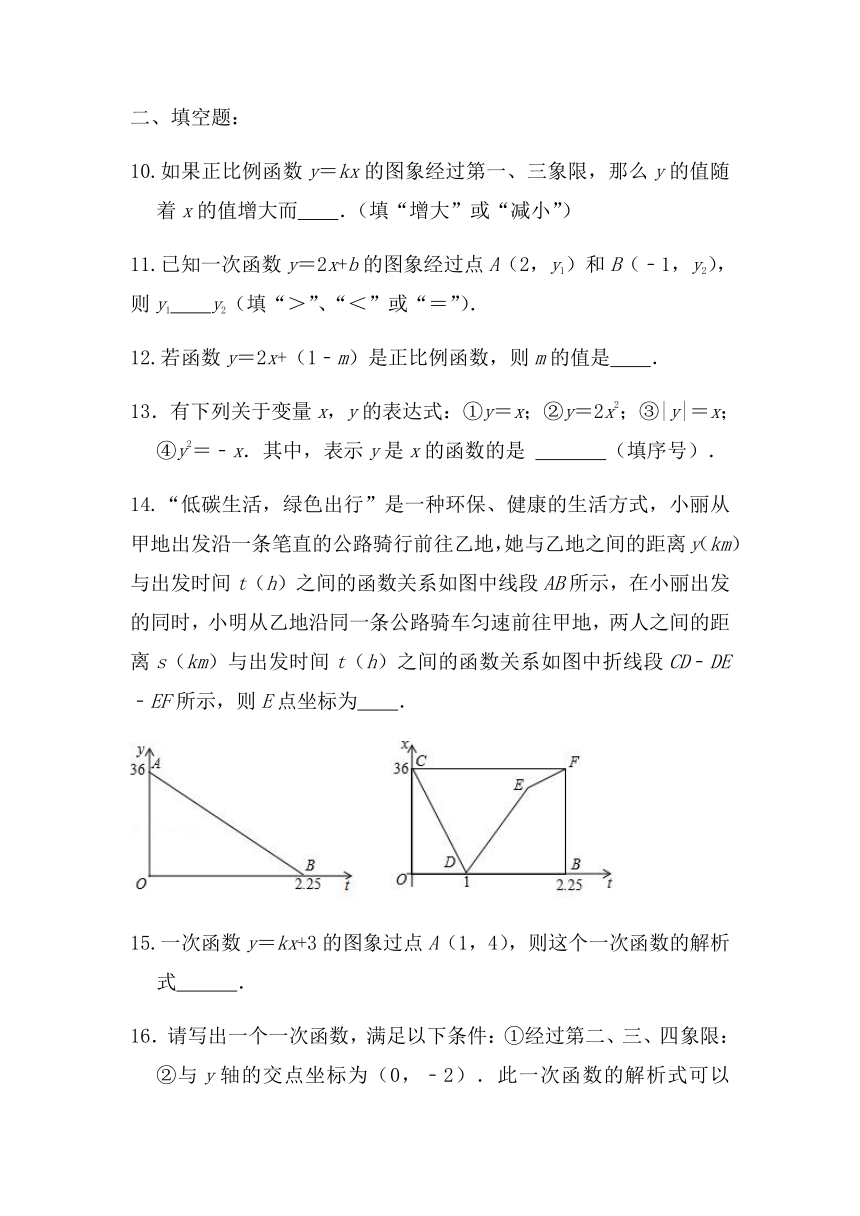
14.“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地出发沿一条笔直的公路骑行前往乙地,她与乙地之间的距离y(km)与出发时间t(h)之间的函数关系如图中线段AB所示,在小丽出发的同时,小明从乙地沿同一条公路骑车匀速前往甲地,两人之间的距离s(km)与出发时间t(h)之间的函数关系如图中折线段CD﹣DE﹣EF所示,则E点坐标为 .
15.一次函数y=kx+3的图象过点A(1,4),则这个一次函数的解析式 .
16.请写出一个一次函数,满足以下条件:①经过第二、三、四象限:②与y轴的交点坐标为(0,﹣2).此一次函数的解析式可以是 .
17.已知y是x的函数,用列表法给出部分x与y的值,表中“▲”处的数是 .
x 1 2 3 4 6
y ▲ 6 4 3 2
三、解答题:
18.已知y=(m﹣2)x+|m|﹣2.
(1)m满足什么条件时,y=(m﹣2)x+|m|﹣2是一次函数?
(2)m满足什么条件时,y=(m﹣2)x+|m|﹣2是正比例函数?
19.“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地匀速步行前往乙地,同时,小明从乙地沿同一路线匀速步行前往甲地,两人之间的距离y(m)与步行时间x(min)之间的函数关系式如图中折线段AB﹣BC﹣CD所示.
(1)小丽与小明出发 min相遇;
(2)在步行过程中,若小明先到达甲地.
①求小丽和小明步行的速度各是多少?
②计算出点C的坐标,并解释点C的实际意义.
20.一只纸箱质量为1kg,当放入一些苹果(每个苹果的质量为0.25kg)后,纸箱和苹果的总质量不超过10kg.
(1)填表:
苹果数/个 8 20 30 36
总质量/kg
(2)设苹果数是x个,纸箱和苹果总质量为ykg,则y与x的关系式是 ;
(3)请估计这只纸箱内最多能装多少个苹果.
21.有这样一个问题:探究函数y=|x+1|的图象与性质.
小强根据学习函数的经验,对函数y=|x+1|的图象与性质进行了探究.下面是小强的探究过程,请补充完整:
(1)在函数y=|x+1|中,自变量x的取值范围是 ;
下表是y与x的几组对应值.
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 …
y … 3 2 1 0 1 m 3 4 …
①求m的值;
②如图,在平面直角坐标系xOy中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
(2)结合函数图象,写出该函数的一条性质: .
22.一科研小组想研究气温T(℃)随高度h(km)的变化规律,已测定地面气温是20℃,若每升高1km,则气温下降6℃.用含h的式子表示T,指出其中的常量与变量,并求出高度分别为1km,5km,7km时的气温.
23.“守护碧水蓝天,守护我们的家园”,某市为了改善城市环境,预算116万元购进A、B两种型号的清扫机,已知A型号清扫机的单价比B型号清扫机单价的多1.2万元,若购进2台A型号清扫机和3台B型号清扫机花费54.6万元.
(1)求A型号清扫机和B型号清扫机的单价分别为多少万元;
(2)该市通过考察决定先购进两种型号的清扫机共10台,且B型号的清扫机数量不能少于A型号清扫机的1.5倍,该市怎样购买才能花费最少?最少花费多少万元?
参考答案
1.C.
2.A
3.D.
4.D.
5.A
6.A.
7.B.
8.C
9.C.
10.增大.
11.>
12.1.
13.①②.
14.(,).
15.y=x+3
16.y=﹣x﹣2(答案不唯一).
17.12.
18.解:(1)由题意得:m﹣2≠0,
解得:m≠2
(2)由题意得:|m|﹣2=0,且m﹣2≠0,
解得:m=﹣2.
19.30
解:(1)由图象可得小丽与小明出发30min相遇,
故答案为:30;
(2)①设小丽步行的速度为V1m/min,小明步行的速度为V2m/min,且V2>V1,
则,
解得:,
答:小丽步行的速度为80m/min,小明步行的速度为100m/min;
②解法一:设点C的坐标为(x,y),
则可得方程(100+80)(x﹣30)+80(67.5﹣x)=5400,
解得x=54,y=(100+80)(54﹣30)=4320m,
解法二:5400÷100=54,54×80=4320,
∴点C(54,4320),
点C表示:两人出发54min时,小明到达甲地,此时两人相距4320m.
20.解:(1)1+0.25×8=3(kg),
1+0.25×20=6(kg),
1+0.25×30=8.5(kg),
1+0.25×36=10(kg),
填表如下:
苹果数/个 8 20 30 36
总质量/kg 3 6 8.5 10
故答案为:3,6,8.5,10;
(2)根据题意,得y=1+0.25x;
故答案为:y=1+0.25x;
(3)设这只纸箱内装了x个苹果,根据题意得
0.25x+1≤10
解得x≤36
所以的最大值是36.
答:估计这只纸箱内最多能装36个苹果.
21.x为任意实数;当x<-1时,y随x的增大而减小;当x>-1时,y随x的增大而增大
解:(1)在函数y=|x+1|中,自变量x的取值范围是x为任意实数,
故答案为:x为任意实数;
①当x=1时,m=|1+1|=2,
即m的值是2;
②如下图所示;
(2)由函数图象可得,
当x<﹣1时,y随x的增大而减小;
当x>﹣1时,y随x的增大而增大.
故答案为:当x<﹣1时,y随x的增大而减小;当x>﹣1时,y随x的增大而增大.
22.解:由地面气温为20℃,如果每升高1km,气温下降6℃,
得T=﹣6h+20,常量是﹣6和20,变量是T,h,
当h=1km时,T=﹣6×1+20=14(℃),
当h=5km时,T=﹣6×5+20=﹣10(℃),
当h=7km时,T=﹣6×7+20=﹣22(℃).
23.解:(1)设B型号清扫机的单价为x万元,则A型号清扫机的单价为()万元,根据题意得
,
解得x=11.6,
(万元),
答:A型号清扫机的单价为9.9万元,型号清扫机的单价为11.6万元;
(2)设购进A型号清扫机a台,总花费为W元,根据题意得
10﹣a≥1.5a,
解得a≤4,
W=9.9a+11.6(10﹣a)=﹣1.7a+116,
∵k=﹣1.7<0,
∴W随a的增大而减小,
∴当购进A型号清扫机4台时花费最少,最少花费为:﹣1.7×4+116=109.2(万元).
答:当购进A型号清扫机4台,B型号的清扫机6台时花费最少,最少花费为109.2万元.
一、选择题:
1.在以x为自变量、y为函数的关系式y=2πx中,常量为( )
A.2 B.π C.2π D.πx
2.在函数y=中,自变量x的取值范围是( )
A.x≠2 B.x≥2 C.x≤2 D.x>2
3.若正比例函数y=(2﹣k)x的图象经过第二、四象限,则k的取值范围是( )
A.k<﹣2 B.k<2 C.k>﹣2 D.k>2
4.在下面的两种相关联的量,成比例的是( )
A.和是15的两个加数 B.一个人的年龄和身高
C.长方形的宽一定,周长和长 D.单价一定,买乒乓球的个数和钱数
5.将直线y=2x﹣3向右平移2个单位,再向上平移3个单位后,所得的直线的表达式为( )
A.y=2x﹣4 B.y=2x+4 C.y=2x+2 D.y=2x﹣2
6.在全民健身越野赛中,甲乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:①前半小时甲选手的速度为8千米/时;②第1小时两人都跑了10千米;③甲比乙先到达终点;④甲选手的速度一直比乙慢.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
7.根据如图所示的计算程序计算函数y的值,若输入m=﹣1,n=2时,则输出y的值是3,若输入m=4,n=3时,则输出y的值是( )
A.﹣5 B.﹣1 C.1 D.13
8.在平面直角坐标系中,若直线y=kx+b经过第一、三、四象限,则直线y=bx+k不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.若实数a,b,c满足,则直线y=kx+k必经过第( )象限.
A.一、二、三 B.一、三 C.二、三 D.二、四
二、填空题:
10.如果正比例函数y=kx的图象经过第一、三象限,那么y的值随着x的值增大而 .(填“增大”或“减小”)
11.已知一次函数y=2x+b的图象经过点A(2,y1)和B(﹣1,y2),则y1 y2(填“>”、“<”或“=”).
12.若函数y=2x+(1﹣m)是正比例函数,则m的值是 .
13.有下列关于变量x,y的表达式:①y=x;②y=2x2;③|y|=x;④y2=﹣x.其中,表示y是x的函数的是 (填序号).
14.“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地出发沿一条笔直的公路骑行前往乙地,她与乙地之间的距离y(km)与出发时间t(h)之间的函数关系如图中线段AB所示,在小丽出发的同时,小明从乙地沿同一条公路骑车匀速前往甲地,两人之间的距离s(km)与出发时间t(h)之间的函数关系如图中折线段CD﹣DE﹣EF所示,则E点坐标为 .
15.一次函数y=kx+3的图象过点A(1,4),则这个一次函数的解析式 .
16.请写出一个一次函数,满足以下条件:①经过第二、三、四象限:②与y轴的交点坐标为(0,﹣2).此一次函数的解析式可以是 .
17.已知y是x的函数,用列表法给出部分x与y的值,表中“▲”处的数是 .
x 1 2 3 4 6
y ▲ 6 4 3 2
三、解答题:
18.已知y=(m﹣2)x+|m|﹣2.
(1)m满足什么条件时,y=(m﹣2)x+|m|﹣2是一次函数?
(2)m满足什么条件时,y=(m﹣2)x+|m|﹣2是正比例函数?
19.“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地匀速步行前往乙地,同时,小明从乙地沿同一路线匀速步行前往甲地,两人之间的距离y(m)与步行时间x(min)之间的函数关系式如图中折线段AB﹣BC﹣CD所示.
(1)小丽与小明出发 min相遇;
(2)在步行过程中,若小明先到达甲地.
①求小丽和小明步行的速度各是多少?
②计算出点C的坐标,并解释点C的实际意义.
20.一只纸箱质量为1kg,当放入一些苹果(每个苹果的质量为0.25kg)后,纸箱和苹果的总质量不超过10kg.
(1)填表:
苹果数/个 8 20 30 36
总质量/kg
(2)设苹果数是x个,纸箱和苹果总质量为ykg,则y与x的关系式是 ;
(3)请估计这只纸箱内最多能装多少个苹果.
21.有这样一个问题:探究函数y=|x+1|的图象与性质.
小强根据学习函数的经验,对函数y=|x+1|的图象与性质进行了探究.下面是小强的探究过程,请补充完整:
(1)在函数y=|x+1|中,自变量x的取值范围是 ;
下表是y与x的几组对应值.
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 …
y … 3 2 1 0 1 m 3 4 …
①求m的值;
②如图,在平面直角坐标系xOy中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
(2)结合函数图象,写出该函数的一条性质: .
22.一科研小组想研究气温T(℃)随高度h(km)的变化规律,已测定地面气温是20℃,若每升高1km,则气温下降6℃.用含h的式子表示T,指出其中的常量与变量,并求出高度分别为1km,5km,7km时的气温.
23.“守护碧水蓝天,守护我们的家园”,某市为了改善城市环境,预算116万元购进A、B两种型号的清扫机,已知A型号清扫机的单价比B型号清扫机单价的多1.2万元,若购进2台A型号清扫机和3台B型号清扫机花费54.6万元.
(1)求A型号清扫机和B型号清扫机的单价分别为多少万元;
(2)该市通过考察决定先购进两种型号的清扫机共10台,且B型号的清扫机数量不能少于A型号清扫机的1.5倍,该市怎样购买才能花费最少?最少花费多少万元?
参考答案
1.C.
2.A
3.D.
4.D.
5.A
6.A.
7.B.
8.C
9.C.
10.增大.
11.>
12.1.
13.①②.
14.(,).
15.y=x+3
16.y=﹣x﹣2(答案不唯一).
17.12.
18.解:(1)由题意得:m﹣2≠0,
解得:m≠2
(2)由题意得:|m|﹣2=0,且m﹣2≠0,
解得:m=﹣2.
19.30
解:(1)由图象可得小丽与小明出发30min相遇,
故答案为:30;
(2)①设小丽步行的速度为V1m/min,小明步行的速度为V2m/min,且V2>V1,
则,
解得:,
答:小丽步行的速度为80m/min,小明步行的速度为100m/min;
②解法一:设点C的坐标为(x,y),
则可得方程(100+80)(x﹣30)+80(67.5﹣x)=5400,
解得x=54,y=(100+80)(54﹣30)=4320m,
解法二:5400÷100=54,54×80=4320,
∴点C(54,4320),
点C表示:两人出发54min时,小明到达甲地,此时两人相距4320m.
20.解:(1)1+0.25×8=3(kg),
1+0.25×20=6(kg),
1+0.25×30=8.5(kg),
1+0.25×36=10(kg),
填表如下:
苹果数/个 8 20 30 36
总质量/kg 3 6 8.5 10
故答案为:3,6,8.5,10;
(2)根据题意,得y=1+0.25x;
故答案为:y=1+0.25x;
(3)设这只纸箱内装了x个苹果,根据题意得
0.25x+1≤10
解得x≤36
所以的最大值是36.
答:估计这只纸箱内最多能装36个苹果.
21.x为任意实数;当x<-1时,y随x的增大而减小;当x>-1时,y随x的增大而增大
解:(1)在函数y=|x+1|中,自变量x的取值范围是x为任意实数,
故答案为:x为任意实数;
①当x=1时,m=|1+1|=2,
即m的值是2;
②如下图所示;
(2)由函数图象可得,
当x<﹣1时,y随x的增大而减小;
当x>﹣1时,y随x的增大而增大.
故答案为:当x<﹣1时,y随x的增大而减小;当x>﹣1时,y随x的增大而增大.
22.解:由地面气温为20℃,如果每升高1km,气温下降6℃,
得T=﹣6h+20,常量是﹣6和20,变量是T,h,
当h=1km时,T=﹣6×1+20=14(℃),
当h=5km时,T=﹣6×5+20=﹣10(℃),
当h=7km时,T=﹣6×7+20=﹣22(℃).
23.解:(1)设B型号清扫机的单价为x万元,则A型号清扫机的单价为()万元,根据题意得
,
解得x=11.6,
(万元),
答:A型号清扫机的单价为9.9万元,型号清扫机的单价为11.6万元;
(2)设购进A型号清扫机a台,总花费为W元,根据题意得
10﹣a≥1.5a,
解得a≤4,
W=9.9a+11.6(10﹣a)=﹣1.7a+116,
∵k=﹣1.7<0,
∴W随a的增大而减小,
∴当购进A型号清扫机4台时花费最少,最少花费为:﹣1.7×4+116=109.2(万元).
答:当购进A型号清扫机4台,B型号的清扫机6台时花费最少,最少花费为109.2万元.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
