2021-2022学年北师大版九年级数学下册 期末综合复习训练(1)3.4圆周角与圆心角的关系 (word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册 期末综合复习训练(1)3.4圆周角与圆心角的关系 (word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 443.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 19:22:31 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3.4圆周角与圆心角的关系》
期末综合复习训练1(附答案)
1.如图,AB是半圆的直径,点C是弧AB的中点,点E是弧AC的中点,连接EB,CA交于点F,则=( )
A. B. C.1﹣ D.
2.如图,半圆的直径AB=10cm,弦AC=6cm,把AC沿直线AD对折恰好与AB重合,则AD的长为( )
A.4cm B.3cm C.5cm D.8cm
3.如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数为( )
A.25° B.50° C.65° D.75°
4.如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则tan∠CBD的值等于( )
A. B. C. D.
5.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
B.1
C. D.﹣1
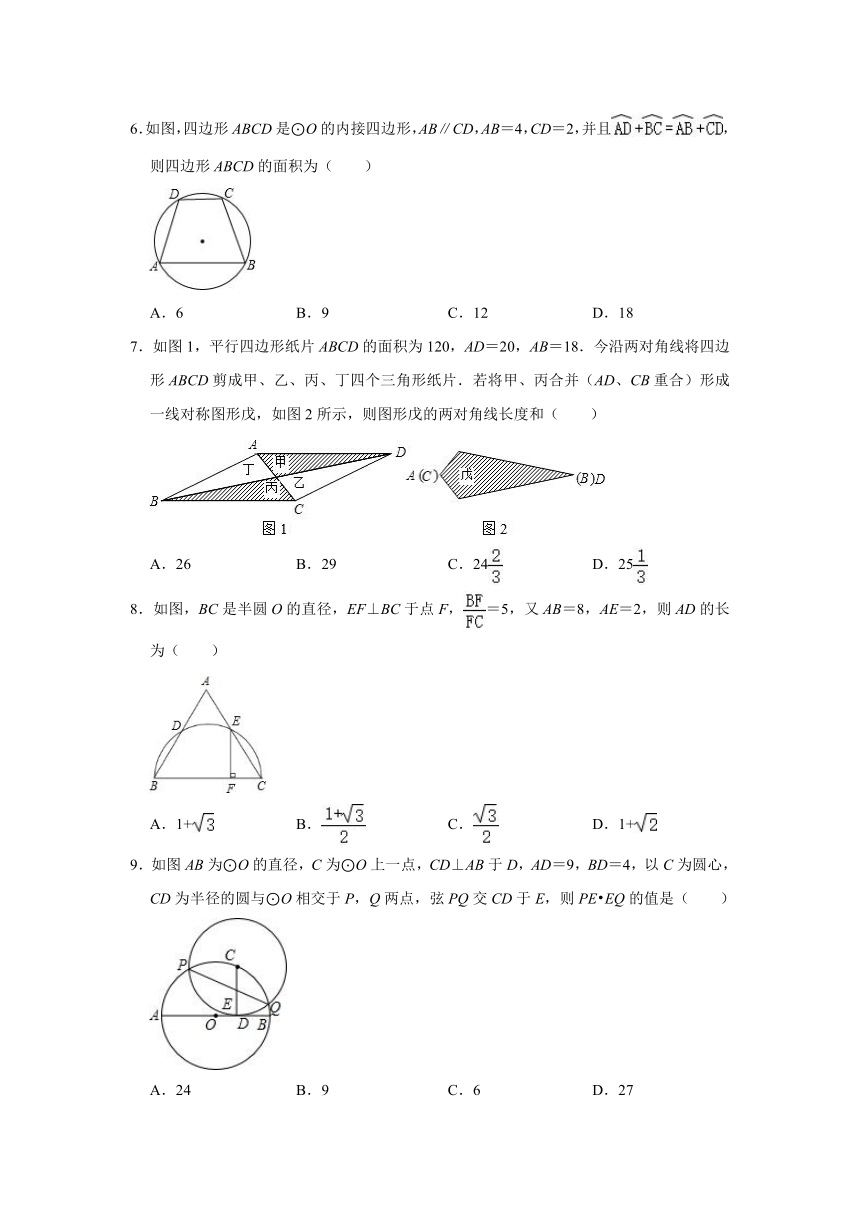
6.如图,四边形ABCD是⊙O的内接四边形,AB∥CD,AB=4,CD=2,并且,则四边形ABCD的面积为( )
A.6 B.9 C.12 D.18
7.如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一线对称图形戊,如图2所示,则图形戊的两对角线长度和( )
A.26 B.29 C.24 D.25
8.如图,BC是半圆O的直径,EF⊥BC于点F,=5,又AB=8,AE=2,则AD的长为( )
A.1+ B. C. D.1+
9.如图AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE EQ的值是( )
A.24 B.9 C.6 D.27
10.如图,已知⊙O的两条弦AB、CD相交于AB的中点E,且AB=4,DE=CE+3,则CD的长为( )
A.4 B.5 C.8 D.10
11.如图,已知A、B两点的坐标分别为(,0)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为 .
12.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 .
13.△ABC是⊙O的内接三角形,∠BAC=60°,D是的中点,AD=a,则四边形ABDC的面积为 .
14.已知四边形ABCD内接于⊙O,且∠A:∠C=1:2,则∠BOD= 度.
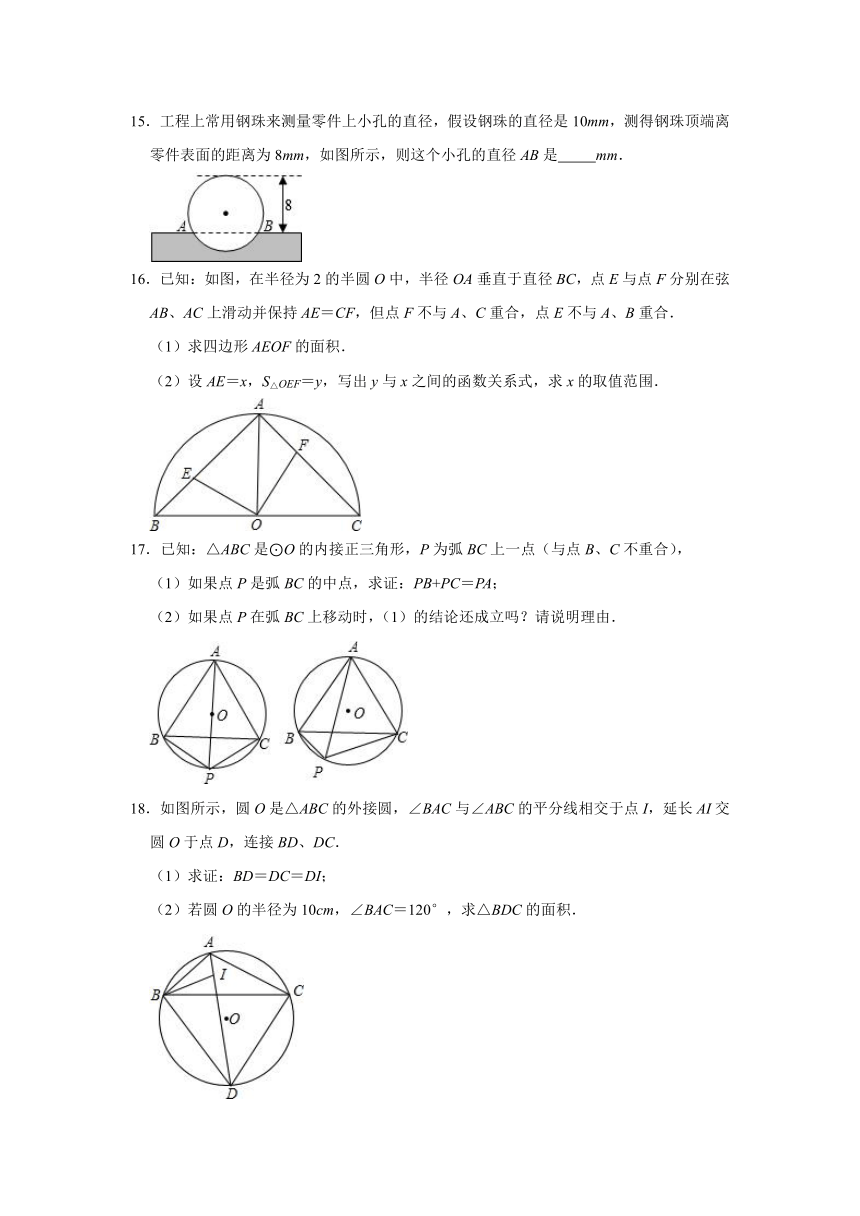
15.工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小孔的直径AB是 mm.
16.已知:如图,在半径为2的半圆O中,半径OA垂直于直径BC,点E与点F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
(1)求四边形AEOF的面积.
(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式,求x的取值范围.
17.已知:△ABC是⊙O的内接正三角形,P为弧BC上一点(与点B、C不重合),
(1)如果点P是弧BC的中点,求证:PB+PC=PA;
(2)如果点P在弧BC上移动时,(1)的结论还成立吗?请说明理由.
18.如图所示,圆O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交圆O于点D,连接BD、DC.
(1)求证:BD=DC=DI;
(2)若圆O的半径为10cm,∠BAC=120°,求△BDC的面积.
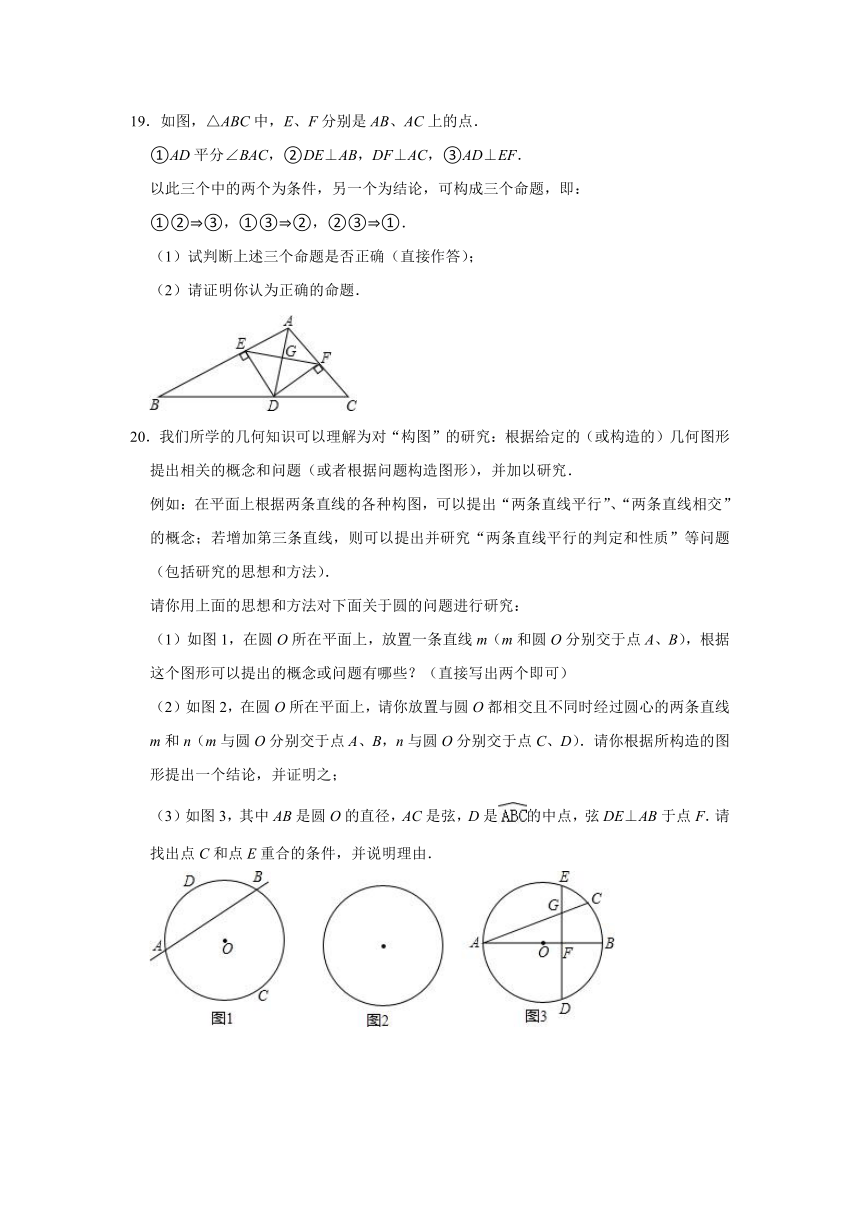
19.如图,△ABC中,E、F分别是AB、AC上的点.
①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF.
以此三个中的两个为条件,另一个为结论,可构成三个命题,即:
①② ③,①③ ②,②③ ①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请证明你认为正确的命题.
20.我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)几何图形提出相关的概念和问题(或者根据问题构造图形),并加以研究.
例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).
请你用上面的思想和方法对下面关于圆的问题进行研究:
(1)如图1,在圆O所在平面上,放置一条直线m(m和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些?(直接写出两个即可)
(2)如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线m和n(m与圆O分别交于点A、B,n与圆O分别交于点C、D).请你根据所构造的图形提出一个结论,并证明之;
(3)如图3,其中AB是圆O的直径,AC是弦,D是的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
参考答案
1.解:方法1:连接AE、CE.作AD∥CE,交BE于D.
∵点E是弧AC的中点,
∴可设AE=CE=1,
根据平行线的性质得∠ADE=∠CED=45°.
∴△ADE是等腰直角三角形,
则AD=,BD=AD=.
所以BE=+1.
再根据两角对应相等得△AEF∽△BEA,
则EF==﹣1,BF=2.
所以=.
方法2:过点C作CO⊥AB于点O,
∵AB是半圆的直径,点C是弧AB的中点,
∴点O是圆心.
连接OE,BC,OE与AC交于点M,
∵E为弧AC的中点,
易证OE⊥AC,
∵∠ACB=90°,∠AOE=45°,
∴OE∥BC,
设OM=1,则AM=1,
∴AC=BC=2,OA=,
∴OE=,
∴EM=﹣1,
∵OE∥BC,
∴==.
故选:D.
2.解:设圆的圆心是O,连接OD,AD,作DE⊥AB于E,OF⊥AC于F.
根据题意知,∠CAD=∠BAD,
∴=,
∴点D是弧BC的中点.
∴∠DOB=∠OAC=2∠BAD,
∴△AOF≌△OED,
∴OE=AF=3cm,
∴DE=4cm,
∴AD==4cm.
故选:A.
3.解:∵∠ABC=25°,
∴∠ADC=25°,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD=90°﹣25°=65°.
故选:C.
4.解:过B作⊙O的直径BM,连接AM;
则有:∠MAB=∠CDB=90°,∠M=∠C;
∴∠MBA=∠CBD;
过O作OE⊥AB于E;
Rt△OEB中,BE=AB=4,OB=5;
由勾股定理,得:OE=3;
∴tan∠MBA==;
因此tan∠CBD=tan∠MBA=,故选D.
5.解:连接AE,
∵以AD为直径的圆交BD于点E,
∴∠AED=90°,
∴点E在以AB为直径的圆O上,
连接OE,OC,
则CE≥OC﹣OE,
∵∠BAC=90°,AB=AC,
∴AC=AB=BC=2,
由勾股定理得,OC==,
∴线段CE长度的最小值为﹣1,
故选:D.
6.解:过O点作DC的垂线交DC于E,交AB于F,交⊙O于M,N,连OD,OA,如图,
∴DE=EC=1,DM弧=MC弧,
∵AB∥CD,
∴OF⊥AB,AD弧=BC弧,
∴AF=BF=2,AN弧=BN弧,
而且,
∴AD弧=DM弧+AN弧,
∴AD弧为半圆MN的一半,
∴∠DOA=90°,
∴Rt△ODE≌Rt△OAF,
∴OE=AF=2,OF=DE=1,即EF=3,
∴梯形ABCD的面积= (2+4) 3=9.
故选:B.
7.解:∵AD=20,平行四边形的面积是120,
∴AD边上的高是6.
∴要求的两对角线长度和是20+6=26.故选:A.
8.解:连接BE.
∵BC是直径.
∴∠AEB=∠BEC=90°
在直角△ABE中,根据勾股定理可得:BE2=AB2﹣AE2=82﹣22=60.
∵=5
∴设FC=x,则BF=5x,BC=6x.
又∵BE2=BF BC
即:30x2=60
解得:x=
∴EC2=FC BC=6x2=12
∴EC=2
∴AC=AE+EC=2+2
∵AD AB=AE AC
∴AD=== 故选:B.
9.解:延长DC交⊙C于M,延长CD交⊙O于N.
∵CD2=AD DB,AD=9,BD=4,
∴CD=6.
在⊙O、⊙C中,由相交弦定理可知,PE EQ=DE EM=CE EN,
设CE=x,则DE=6﹣x,EN=6﹣x+6
则(6﹣x)(x+6)=x(6﹣x+6),
解得x=3.
所以,CE=3,DE=6﹣3=3,EM=6+3=9.
所以PE EQ=3×9=27.
故选:D.
10.解:设CE=x,则DE=3+x.
根据相交弦定理,得x(x+3)=2×2,
x=1或x=﹣4(不合题意,应舍去).
则CD=3+1+1=5.
故选:B.
11.解:∵OB=2,OA=2,
∴AB==4,
∵∠AOP=45°,
∴P点横纵坐标相等,可设为a,即P(a,a),
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,坐标C(,1),
可得P点在圆上,P点到圆心的距离为圆的半径2,
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,
∴∠CFP=90°,
∴PF=a﹣1,CF=a﹣,PC=2,
∴在Rt△PCF中,利用勾股定理得:(a﹣)2+(a﹣1)2=22,
舍去不合适的根,可得:a=1+,
则P点坐标为(+1,+1).
∵P与P′关于圆心(,1)对称,
∴P′(﹣1,1﹣).
故答案为:(+1,+1)或(﹣1,1﹣)
12.解:作点B关于MN的对称点C,连接AC交MN于点P,连接OB,则P点就是所求作的点.
此时PA+PB最小,且等于AC的长.
连接OA,OC,
∵∠AMN=30°,
∴∠AON=60°,
∵=
∴∠AOB=∠BON=30°,
∵MN⊥BC,
∴=,
∴∠CON=∠NOB=30°,
则∠AOC=90°,又OA=OC=1,
则AC=.
13.解:解法一:在ABDC中,∠BAC=60度,所以∠BDC=120°,
∵点D是弧BC的中点,
∴BD=DC,
∴∠DBC=∠DCB=30°,
在△BDC中用正弦定理,得
∴BC=BD,
设BD=DC=x,那么BC=x,
用托勒密定理:AD BC=AB DC+BD AC,
即ax=x AB+x AC,
则AB+AC=a,
S四边形ABDC=S△ABD+S△ACD=(AB AD sin∠BAD+AC AD sin∠DAC),
=(AB+AC)AD sin30°,
=a2;
解法二:如图,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,
∵D是的中点,
∴BD=CD,∠BAD=∠FAD,
∴DE=DF(角平分线上的点到角的两边的距离相等),
在Rt△DBE与Rt△DCF中,,
∴Rt△DBE≌Rt△DCF(HL),
∴S△DBE=S△DCF,
∴S四边形ABDC=S四边形AEDF,
∵点D是弧BC的中点,∠BAC=60°,
∴∠BAD=∠BAC=×60°=30°,
∵AD=a,
∴AE=AD cos30°=a,
DE=AD sin30 =a,
∴S四边形AEDF=2S△ADE=2××a×a=a2.
故答案为:a2.
14.解:∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°;
又∠A:∠C=1:2,得∠A=60°.
∴∠BOD=2∠A=120°.
故答案为:120.
15.解:钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,
则下面的距离就是2.
利用相交弦定理可得:2×8=AB×AB,
解得AB=8.
故答案为:8.
16.解:(1)∵BC为半圆O的直径,OA为半径,且OA⊥BC,
∴∠B=∠OAF=45°,OA=OB,
又∵AE=CF,AB=AC,
∴BE=AF,
∴△BOE≌△AOF
∴S四边形AEOF=S△AOB=OB OA=2.
(2)∵BC为半圆O的直径,
∴∠BAC=90°,且AB=AC=2,
y=S△OEF=S四边形AEOF﹣S△AEF=2﹣AE AF=2﹣x(2﹣x)
∴y=x2﹣x+2(0<x<2).
17.解:(1)连OB,OC,如图
∵点P是弧BC的中点,△ABC是⊙O的内接正三角形,
∴AP为⊙O的直径,
∴∠BPO=∠ACB,∠APC=∠ABC,
∵△ABC是⊙O的内接正三角形,
∴∠ACB=∠ABC=60°,
∴∠BPO=∠APC=60°,
∴△OBP和△OPC都是等边三角形,
∴PB=PC=OP=OA,
∴PB+PC=PA;
(2)(1)的结论还成立.理由如下:
截取PE=PC,
∵∠APC=60°,
∴△PEC为等边三角形,
∴CE=CP,∠PCE=60°,
而∠ACB=60°,
∴∠ACE=∠BCP,
而CA=CB,
∴△CAE≌△CBP,
∴AE=PB,
∴PB+PC=PA.
18.(1)证明:∵AI平分∠BAC,
∴∠BAD=∠DAC,
∴=,
∴BD=DC.
∵BI平分∠ABC,
∴∠ABI=∠CBI.
∵∠BAD=∠DAC,∠DBC=∠DAC,
∴∠BAD=∠DBC.
又∵∠DBI=∠DBC+∠CBI,∠DIB=∠ABI+∠BAD,
∴∠DBI=∠DIB,
∴△BDI为等腰三角形,
∴BD=ID,
∴BD=DC=DI.
(2)解:当∠BAC=120°时,△ABC为钝角三角形,
∴圆心O在△ABC外.
连接OB、OD、OC.
∵BD=CD,
∴=,
∴∠DOC=∠BOD=2∠BAD=120°,
∴∠DBC=∠DCB=60°,
∴△BDC为正三角形.
延长CO交BD于点E,则OE⊥BD,
∴BE=BD,
又∵OB=10,
∴BD=2OBcos30°=2×10×=10.
∴CE=CD sin60°=BD sin60°=10×=15,
∴S△BDC=BD CE=×10×15=75.
答:△BDC的面积为75cm2.
19.解:(1)①② ③,正确;①③ ②,错误;②③ ①,正确.
(2)先证①② ③.如图.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,AD=AD,
∴Rt△ADE≌Rt△ADF.
∴DE=DF,∠ADE=∠ADF.
设AD与EF交于G,则△DEG≌△DFG,
∴∠DGE=∠DGF.
∴∠DGE=∠DGF=90°.
∴AD⊥EF.
再证②③ ①.如图2,
设AD的中点为O,连接OE,OF,
∵DE⊥AB,DF⊥AC,
∴OE,OF分别是Rt△ADE,Rt△ADF斜边上的中线.
∴OE=AD,OF=AD.
即点O到A、E、D、F的距离相等.
∴四点A、E、D、F在以O为圆心,AD为半径的圆上,AD是直径.
∴EF是⊙O的弦.
∵EF⊥AD,
∴∠DAE=∠DAF.
即AD平分∠BAC.
20.解:(1)弦(图中线段AB)、弧(图中的ACB弧)、弓形、求弓形的面积(因为是封闭图形)等.
(写对一个给(1分),写对两个给2分)
(2)如图,AB为弦,CD为弦,且AB与CD在圆内相交于点P.
结论:PA PB=PC PD.
证明:连接AD,BC,
∵∠APD=∠BPC,∠D=∠B
∴△APD∽△BPC
∴PA PB=PC PD;
(3)若点C和点E重合,
则由圆的对称性,知点C和点D关于直径AB对称,(8分)
设∠BAC=x,则∠BAD=x,∠ABC=90°﹣x,(9分)
又D是的中点,所以2∠CAD=∠CAD+∠ACD=180°﹣∠ABC,
即2 2x=180°﹣(90°﹣x),(10分)
解得x=∠BAC=30°.(11分)
(若求得AC=AB或AF=3 FB等也可,评分可参照上面的标准;也可以先直觉猜测点B、C是圆的十二等分点,然后说明.)
期末综合复习训练1(附答案)
1.如图,AB是半圆的直径,点C是弧AB的中点,点E是弧AC的中点,连接EB,CA交于点F,则=( )
A. B. C.1﹣ D.
2.如图,半圆的直径AB=10cm,弦AC=6cm,把AC沿直线AD对折恰好与AB重合,则AD的长为( )
A.4cm B.3cm C.5cm D.8cm
3.如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数为( )
A.25° B.50° C.65° D.75°
4.如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则tan∠CBD的值等于( )
A. B. C. D.
5.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
B.1
C. D.﹣1
6.如图,四边形ABCD是⊙O的内接四边形,AB∥CD,AB=4,CD=2,并且,则四边形ABCD的面积为( )
A.6 B.9 C.12 D.18
7.如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一线对称图形戊,如图2所示,则图形戊的两对角线长度和( )
A.26 B.29 C.24 D.25
8.如图,BC是半圆O的直径,EF⊥BC于点F,=5,又AB=8,AE=2,则AD的长为( )
A.1+ B. C. D.1+
9.如图AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE EQ的值是( )
A.24 B.9 C.6 D.27
10.如图,已知⊙O的两条弦AB、CD相交于AB的中点E,且AB=4,DE=CE+3,则CD的长为( )
A.4 B.5 C.8 D.10
11.如图,已知A、B两点的坐标分别为(,0)、(0,2),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为 .
12.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 .
13.△ABC是⊙O的内接三角形,∠BAC=60°,D是的中点,AD=a,则四边形ABDC的面积为 .
14.已知四边形ABCD内接于⊙O,且∠A:∠C=1:2,则∠BOD= 度.
15.工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小孔的直径AB是 mm.
16.已知:如图,在半径为2的半圆O中,半径OA垂直于直径BC,点E与点F分别在弦AB、AC上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
(1)求四边形AEOF的面积.
(2)设AE=x,S△OEF=y,写出y与x之间的函数关系式,求x的取值范围.
17.已知:△ABC是⊙O的内接正三角形,P为弧BC上一点(与点B、C不重合),
(1)如果点P是弧BC的中点,求证:PB+PC=PA;
(2)如果点P在弧BC上移动时,(1)的结论还成立吗?请说明理由.
18.如图所示,圆O是△ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交圆O于点D,连接BD、DC.
(1)求证:BD=DC=DI;
(2)若圆O的半径为10cm,∠BAC=120°,求△BDC的面积.
19.如图,△ABC中,E、F分别是AB、AC上的点.
①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF.
以此三个中的两个为条件,另一个为结论,可构成三个命题,即:
①② ③,①③ ②,②③ ①.
(1)试判断上述三个命题是否正确(直接作答);
(2)请证明你认为正确的命题.
20.我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)几何图形提出相关的概念和问题(或者根据问题构造图形),并加以研究.
例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).
请你用上面的思想和方法对下面关于圆的问题进行研究:
(1)如图1,在圆O所在平面上,放置一条直线m(m和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些?(直接写出两个即可)
(2)如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线m和n(m与圆O分别交于点A、B,n与圆O分别交于点C、D).请你根据所构造的图形提出一个结论,并证明之;
(3)如图3,其中AB是圆O的直径,AC是弦,D是的中点,弦DE⊥AB于点F.请找出点C和点E重合的条件,并说明理由.
参考答案
1.解:方法1:连接AE、CE.作AD∥CE,交BE于D.
∵点E是弧AC的中点,
∴可设AE=CE=1,
根据平行线的性质得∠ADE=∠CED=45°.
∴△ADE是等腰直角三角形,
则AD=,BD=AD=.
所以BE=+1.
再根据两角对应相等得△AEF∽△BEA,
则EF==﹣1,BF=2.
所以=.
方法2:过点C作CO⊥AB于点O,
∵AB是半圆的直径,点C是弧AB的中点,
∴点O是圆心.
连接OE,BC,OE与AC交于点M,
∵E为弧AC的中点,
易证OE⊥AC,
∵∠ACB=90°,∠AOE=45°,
∴OE∥BC,
设OM=1,则AM=1,
∴AC=BC=2,OA=,
∴OE=,
∴EM=﹣1,
∵OE∥BC,
∴==.
故选:D.
2.解:设圆的圆心是O,连接OD,AD,作DE⊥AB于E,OF⊥AC于F.
根据题意知,∠CAD=∠BAD,
∴=,
∴点D是弧BC的中点.
∴∠DOB=∠OAC=2∠BAD,
∴△AOF≌△OED,
∴OE=AF=3cm,
∴DE=4cm,
∴AD==4cm.
故选:A.
3.解:∵∠ABC=25°,
∴∠ADC=25°,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD=90°﹣25°=65°.
故选:C.
4.解:过B作⊙O的直径BM,连接AM;
则有:∠MAB=∠CDB=90°,∠M=∠C;
∴∠MBA=∠CBD;
过O作OE⊥AB于E;
Rt△OEB中,BE=AB=4,OB=5;
由勾股定理,得:OE=3;
∴tan∠MBA==;
因此tan∠CBD=tan∠MBA=,故选D.
5.解:连接AE,
∵以AD为直径的圆交BD于点E,
∴∠AED=90°,
∴点E在以AB为直径的圆O上,
连接OE,OC,
则CE≥OC﹣OE,
∵∠BAC=90°,AB=AC,
∴AC=AB=BC=2,
由勾股定理得,OC==,
∴线段CE长度的最小值为﹣1,
故选:D.
6.解:过O点作DC的垂线交DC于E,交AB于F,交⊙O于M,N,连OD,OA,如图,
∴DE=EC=1,DM弧=MC弧,
∵AB∥CD,
∴OF⊥AB,AD弧=BC弧,
∴AF=BF=2,AN弧=BN弧,
而且,
∴AD弧=DM弧+AN弧,
∴AD弧为半圆MN的一半,
∴∠DOA=90°,
∴Rt△ODE≌Rt△OAF,
∴OE=AF=2,OF=DE=1,即EF=3,
∴梯形ABCD的面积= (2+4) 3=9.
故选:B.
7.解:∵AD=20,平行四边形的面积是120,
∴AD边上的高是6.
∴要求的两对角线长度和是20+6=26.故选:A.
8.解:连接BE.
∵BC是直径.
∴∠AEB=∠BEC=90°
在直角△ABE中,根据勾股定理可得:BE2=AB2﹣AE2=82﹣22=60.
∵=5
∴设FC=x,则BF=5x,BC=6x.
又∵BE2=BF BC
即:30x2=60
解得:x=
∴EC2=FC BC=6x2=12
∴EC=2
∴AC=AE+EC=2+2
∵AD AB=AE AC
∴AD=== 故选:B.
9.解:延长DC交⊙C于M,延长CD交⊙O于N.
∵CD2=AD DB,AD=9,BD=4,
∴CD=6.
在⊙O、⊙C中,由相交弦定理可知,PE EQ=DE EM=CE EN,
设CE=x,则DE=6﹣x,EN=6﹣x+6
则(6﹣x)(x+6)=x(6﹣x+6),
解得x=3.
所以,CE=3,DE=6﹣3=3,EM=6+3=9.
所以PE EQ=3×9=27.
故选:D.
10.解:设CE=x,则DE=3+x.
根据相交弦定理,得x(x+3)=2×2,
x=1或x=﹣4(不合题意,应舍去).
则CD=3+1+1=5.
故选:B.
11.解:∵OB=2,OA=2,
∴AB==4,
∵∠AOP=45°,
∴P点横纵坐标相等,可设为a,即P(a,a),
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,坐标C(,1),
可得P点在圆上,P点到圆心的距离为圆的半径2,
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,
∴∠CFP=90°,
∴PF=a﹣1,CF=a﹣,PC=2,
∴在Rt△PCF中,利用勾股定理得:(a﹣)2+(a﹣1)2=22,
舍去不合适的根,可得:a=1+,
则P点坐标为(+1,+1).
∵P与P′关于圆心(,1)对称,
∴P′(﹣1,1﹣).
故答案为:(+1,+1)或(﹣1,1﹣)
12.解:作点B关于MN的对称点C,连接AC交MN于点P,连接OB,则P点就是所求作的点.
此时PA+PB最小,且等于AC的长.
连接OA,OC,
∵∠AMN=30°,
∴∠AON=60°,
∵=
∴∠AOB=∠BON=30°,
∵MN⊥BC,
∴=,
∴∠CON=∠NOB=30°,
则∠AOC=90°,又OA=OC=1,
则AC=.
13.解:解法一:在ABDC中,∠BAC=60度,所以∠BDC=120°,
∵点D是弧BC的中点,
∴BD=DC,
∴∠DBC=∠DCB=30°,
在△BDC中用正弦定理,得
∴BC=BD,
设BD=DC=x,那么BC=x,
用托勒密定理:AD BC=AB DC+BD AC,
即ax=x AB+x AC,
则AB+AC=a,
S四边形ABDC=S△ABD+S△ACD=(AB AD sin∠BAD+AC AD sin∠DAC),
=(AB+AC)AD sin30°,
=a2;
解法二:如图,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,
∵D是的中点,
∴BD=CD,∠BAD=∠FAD,
∴DE=DF(角平分线上的点到角的两边的距离相等),
在Rt△DBE与Rt△DCF中,,
∴Rt△DBE≌Rt△DCF(HL),
∴S△DBE=S△DCF,
∴S四边形ABDC=S四边形AEDF,
∵点D是弧BC的中点,∠BAC=60°,
∴∠BAD=∠BAC=×60°=30°,
∵AD=a,
∴AE=AD cos30°=a,
DE=AD sin30 =a,
∴S四边形AEDF=2S△ADE=2××a×a=a2.
故答案为:a2.
14.解:∵四边形ABCD内接于⊙O,
∴∠A+∠C=180°;
又∠A:∠C=1:2,得∠A=60°.
∴∠BOD=2∠A=120°.
故答案为:120.
15.解:钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,
则下面的距离就是2.
利用相交弦定理可得:2×8=AB×AB,
解得AB=8.
故答案为:8.
16.解:(1)∵BC为半圆O的直径,OA为半径,且OA⊥BC,
∴∠B=∠OAF=45°,OA=OB,
又∵AE=CF,AB=AC,
∴BE=AF,
∴△BOE≌△AOF
∴S四边形AEOF=S△AOB=OB OA=2.
(2)∵BC为半圆O的直径,
∴∠BAC=90°,且AB=AC=2,
y=S△OEF=S四边形AEOF﹣S△AEF=2﹣AE AF=2﹣x(2﹣x)
∴y=x2﹣x+2(0<x<2).
17.解:(1)连OB,OC,如图
∵点P是弧BC的中点,△ABC是⊙O的内接正三角形,
∴AP为⊙O的直径,
∴∠BPO=∠ACB,∠APC=∠ABC,
∵△ABC是⊙O的内接正三角形,
∴∠ACB=∠ABC=60°,
∴∠BPO=∠APC=60°,
∴△OBP和△OPC都是等边三角形,
∴PB=PC=OP=OA,
∴PB+PC=PA;
(2)(1)的结论还成立.理由如下:
截取PE=PC,
∵∠APC=60°,
∴△PEC为等边三角形,
∴CE=CP,∠PCE=60°,
而∠ACB=60°,
∴∠ACE=∠BCP,
而CA=CB,
∴△CAE≌△CBP,
∴AE=PB,
∴PB+PC=PA.
18.(1)证明:∵AI平分∠BAC,
∴∠BAD=∠DAC,
∴=,
∴BD=DC.
∵BI平分∠ABC,
∴∠ABI=∠CBI.
∵∠BAD=∠DAC,∠DBC=∠DAC,
∴∠BAD=∠DBC.
又∵∠DBI=∠DBC+∠CBI,∠DIB=∠ABI+∠BAD,
∴∠DBI=∠DIB,
∴△BDI为等腰三角形,
∴BD=ID,
∴BD=DC=DI.
(2)解:当∠BAC=120°时,△ABC为钝角三角形,
∴圆心O在△ABC外.
连接OB、OD、OC.
∵BD=CD,
∴=,
∴∠DOC=∠BOD=2∠BAD=120°,
∴∠DBC=∠DCB=60°,
∴△BDC为正三角形.
延长CO交BD于点E,则OE⊥BD,
∴BE=BD,
又∵OB=10,
∴BD=2OBcos30°=2×10×=10.
∴CE=CD sin60°=BD sin60°=10×=15,
∴S△BDC=BD CE=×10×15=75.
答:△BDC的面积为75cm2.
19.解:(1)①② ③,正确;①③ ②,错误;②③ ①,正确.
(2)先证①② ③.如图.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,AD=AD,
∴Rt△ADE≌Rt△ADF.
∴DE=DF,∠ADE=∠ADF.
设AD与EF交于G,则△DEG≌△DFG,
∴∠DGE=∠DGF.
∴∠DGE=∠DGF=90°.
∴AD⊥EF.
再证②③ ①.如图2,
设AD的中点为O,连接OE,OF,
∵DE⊥AB,DF⊥AC,
∴OE,OF分别是Rt△ADE,Rt△ADF斜边上的中线.
∴OE=AD,OF=AD.
即点O到A、E、D、F的距离相等.
∴四点A、E、D、F在以O为圆心,AD为半径的圆上,AD是直径.
∴EF是⊙O的弦.
∵EF⊥AD,
∴∠DAE=∠DAF.
即AD平分∠BAC.
20.解:(1)弦(图中线段AB)、弧(图中的ACB弧)、弓形、求弓形的面积(因为是封闭图形)等.
(写对一个给(1分),写对两个给2分)
(2)如图,AB为弦,CD为弦,且AB与CD在圆内相交于点P.
结论:PA PB=PC PD.
证明:连接AD,BC,
∵∠APD=∠BPC,∠D=∠B
∴△APD∽△BPC
∴PA PB=PC PD;
(3)若点C和点E重合,
则由圆的对称性,知点C和点D关于直径AB对称,(8分)
设∠BAC=x,则∠BAD=x,∠ABC=90°﹣x,(9分)
又D是的中点,所以2∠CAD=∠CAD+∠ACD=180°﹣∠ABC,
即2 2x=180°﹣(90°﹣x),(10分)
解得x=∠BAC=30°.(11分)
(若求得AC=AB或AF=3 FB等也可,评分可参照上面的标准;也可以先直觉猜测点B、C是圆的十二等分点,然后说明.)
