2021-2022学年高二上学期数学人教A版必修5.2.4 等比数列第一课时 课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版必修5.2.4 等比数列第一课时 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 986.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 16:56:43 | ||
图片预览








文档简介
(共22张PPT)
2.4 等比数列
温故知新
如果一碗面由256根面条组成,请问需要拉面师傅拉几次才能得到
我国古代一些学者提出:“一尺之棰,日取其半,万世不竭。”即一尺长的木棒,每日取其一半,永远也取不完,这样每天剩下的部分都是前一天的一半。如果把“一尺之棰”看成单位“1”,那么得到的数列是
某种汽车购买时的价格是10万元,每年的折旧率是15%,这辆车各年开始时的价值(单位:万元)分别是:
10,10×0.85,10×0.852 ,10×0.853,…
拉面时前9次拉伸成的面条根数构成一个数列:
上面数列有什么共同特点
从第二项起,每一项与前一项的比都等于同一个常数。
1, 2, 4, 8, 16, 32, 64, 128, 256
10,10×0.85,10×0.852 ,10×0.853,…
1, 2, 4, 8, 16, 32, 64, 128, 256
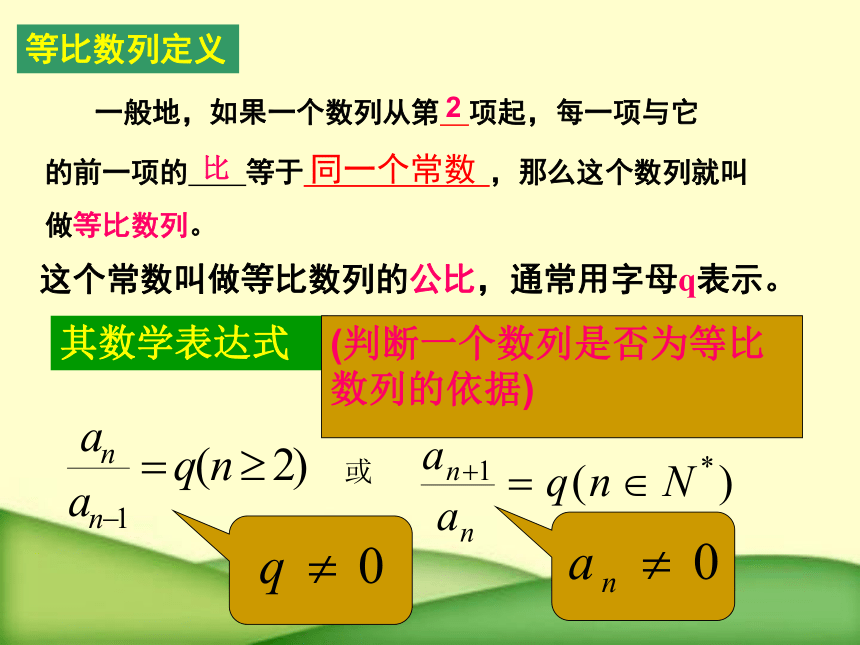
或
其数学表达式
等比数列定义
一般地,如果一个数列从第 项起,每一项与它
的前一项的 等于 ,那么这个数列就叫
做等比数列。
这个常数叫做等比数列的公比,通常用字母q表示。
比
同一个常数
2
(判断一个数列是否为等比数列的依据)
1.已知等比数列{ an }:
(1) an 能不能是零?
(2)公比q能不能是1?
2.用下列方法表示的数列中能确定
是等比数列的是 .
① 1,-1,1,…,(-1)n+1 ; ②1,2,4,6…;
③a,a,a,…,a; ④已知a1=2,an=3an+1 ;
⑤
⑥2a,2a,2a,…,2a.
3.什么样的数列既是等差数列又是等比数列?
不能
能
√
√
√
×
×
×
非零的
常数列
① ④ ⑥
思考1:
思考2:
若a,G,b三个数成等比数列,那么这 三个数有何恒等关系?
结论:G2=ab
G叫做a,b的等比中项
等比中项有两个
名称 等 差 数 列 等 比 数 列
通项公式
……
由此归纳等差数列的通项公式可得:
法1:不完全归纳法
法1:不完全归纳法
……
由此归纳等差数列的通项公式可得:
a1q2
a1q3
a1qn-1
名称 等 差 数 列 等 比 数 列
通项公式
……
把这n-1个式子相加,得:
法2:累加法
当n=1时,a1=a1 上式成立
……
法2: 法
名称 等 差 数 列 等 比 数 列
通项公式
……
把这n-1个式子相加,得:
法2:累加法
当n=1时,上式成立
……
法2: 累乘 法
把这n-1个式子相乘,得:
当n=1时,上式成立
等比数列的通项公式:
(n∈N﹡,q≠0)
例1:在等比数列{an}中:
n=5
a5=
a1=
q=
例2:在等比数列{an}中:
此题解法是利用数学的函数与方程思想,函数与方程思想是数学几个重要思想方法之一,也是高考必考的思想方法,应熟悉并掌握。
名称 等 差 数 列 等 比 数 列
通项公式
引申
可得
已知等差数列{an}中,公差为d,则an与am(n,m ∈ N*)有何关系?
已知等比数列{an}中,公比为q,则an与am(n,m ∈ N*)有何关系?
an=a1qn-1
am=a1qm-1
可得
例2:在等比数列{an}中:
数 列 等 差 数 列 等 比 数 列
定 义
公差(比)
通项公式
引申
类比
小结
例如:数列{an}的首项是a1=1,公比q=2,则通项公式是: ______
上式还可以写成
可见,这个等比数列
的图象都在函数
的图象上,如右图所示。
0 1 2 3 4 n
an
8
7
6
5
4
3
2
1
·
·
·
·
思考4:等比数列的通项公式与函数有怎样的关系?
定义法,只要看
当堂达标:
1.下面有四个结论:
(1)由第一项起乘相同常数得后一项,这样所得到的数列一定为等比数列;
(2)常数列b,b,…b一定为等比数列;
(3)等比数列{ }中,若公比q=1,则此数列各项相等;
(4)等比数列中,各项与公比都不能为零。
其中正确结论的个数是( )
A. 0 B. 1 C. 2 D.3
2. 等比数列{ }中, ,公比q=3,则通项公式( )
A. B. C. D.
3. 在等比数列{ }中, ,则 .
4. 的等比中项为:
C
384
D
数 列 等 差 数 列 等 比 数 列
定 义
公差(比)
通项公式
引申
类比
小结
猜一猜
给你一张足够大的纸,假设其厚度为0.1毫米,那么当你把这张纸对折了51次的时候,所达到的厚度有多少?
猜一猜:
把一张纸折叠51次,得到的大约是地球与太阳之间的距离!
谢 谢 !
2.4 等比数列
温故知新
如果一碗面由256根面条组成,请问需要拉面师傅拉几次才能得到
我国古代一些学者提出:“一尺之棰,日取其半,万世不竭。”即一尺长的木棒,每日取其一半,永远也取不完,这样每天剩下的部分都是前一天的一半。如果把“一尺之棰”看成单位“1”,那么得到的数列是
某种汽车购买时的价格是10万元,每年的折旧率是15%,这辆车各年开始时的价值(单位:万元)分别是:
10,10×0.85,10×0.852 ,10×0.853,…
拉面时前9次拉伸成的面条根数构成一个数列:
上面数列有什么共同特点
从第二项起,每一项与前一项的比都等于同一个常数。
1, 2, 4, 8, 16, 32, 64, 128, 256
10,10×0.85,10×0.852 ,10×0.853,…
1, 2, 4, 8, 16, 32, 64, 128, 256
或
其数学表达式
等比数列定义
一般地,如果一个数列从第 项起,每一项与它
的前一项的 等于 ,那么这个数列就叫
做等比数列。
这个常数叫做等比数列的公比,通常用字母q表示。
比
同一个常数
2
(判断一个数列是否为等比数列的依据)
1.已知等比数列{ an }:
(1) an 能不能是零?
(2)公比q能不能是1?
2.用下列方法表示的数列中能确定
是等比数列的是 .
① 1,-1,1,…,(-1)n+1 ; ②1,2,4,6…;
③a,a,a,…,a; ④已知a1=2,an=3an+1 ;
⑤
⑥2a,2a,2a,…,2a.
3.什么样的数列既是等差数列又是等比数列?
不能
能
√
√
√
×
×
×
非零的
常数列
① ④ ⑥
思考1:
思考2:
若a,G,b三个数成等比数列,那么这 三个数有何恒等关系?
结论:G2=ab
G叫做a,b的等比中项
等比中项有两个
名称 等 差 数 列 等 比 数 列
通项公式
……
由此归纳等差数列的通项公式可得:
法1:不完全归纳法
法1:不完全归纳法
……
由此归纳等差数列的通项公式可得:
a1q2
a1q3
a1qn-1
名称 等 差 数 列 等 比 数 列
通项公式
……
把这n-1个式子相加,得:
法2:累加法
当n=1时,a1=a1 上式成立
……
法2: 法
名称 等 差 数 列 等 比 数 列
通项公式
……
把这n-1个式子相加,得:
法2:累加法
当n=1时,上式成立
……
法2: 累乘 法
把这n-1个式子相乘,得:
当n=1时,上式成立
等比数列的通项公式:
(n∈N﹡,q≠0)
例1:在等比数列{an}中:
n=5
a5=
a1=
q=
例2:在等比数列{an}中:
此题解法是利用数学的函数与方程思想,函数与方程思想是数学几个重要思想方法之一,也是高考必考的思想方法,应熟悉并掌握。
名称 等 差 数 列 等 比 数 列
通项公式
引申
可得
已知等差数列{an}中,公差为d,则an与am(n,m ∈ N*)有何关系?
已知等比数列{an}中,公比为q,则an与am(n,m ∈ N*)有何关系?
an=a1qn-1
am=a1qm-1
可得
例2:在等比数列{an}中:
数 列 等 差 数 列 等 比 数 列
定 义
公差(比)
通项公式
引申
类比
小结
例如:数列{an}的首项是a1=1,公比q=2,则通项公式是: ______
上式还可以写成
可见,这个等比数列
的图象都在函数
的图象上,如右图所示。
0 1 2 3 4 n
an
8
7
6
5
4
3
2
1
·
·
·
·
思考4:等比数列的通项公式与函数有怎样的关系?
定义法,只要看
当堂达标:
1.下面有四个结论:
(1)由第一项起乘相同常数得后一项,这样所得到的数列一定为等比数列;
(2)常数列b,b,…b一定为等比数列;
(3)等比数列{ }中,若公比q=1,则此数列各项相等;
(4)等比数列中,各项与公比都不能为零。
其中正确结论的个数是( )
A. 0 B. 1 C. 2 D.3
2. 等比数列{ }中, ,公比q=3,则通项公式( )
A. B. C. D.
3. 在等比数列{ }中, ,则 .
4. 的等比中项为:
C
384
D
数 列 等 差 数 列 等 比 数 列
定 义
公差(比)
通项公式
引申
类比
小结
猜一猜
给你一张足够大的纸,假设其厚度为0.1毫米,那么当你把这张纸对折了51次的时候,所达到的厚度有多少?
猜一猜:
把一张纸折叠51次,得到的大约是地球与太阳之间的距离!
谢 谢 !
