湖北省京山五中2012-2013学年高二九月月考数学试题
文档属性
| 名称 | 湖北省京山五中2012-2013学年高二九月月考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 310.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-01 08:01:00 | ||
图片预览

文档简介
湖北省京山五中2012-2013学年高二九月月考试题
高二数学
选择题(本大题共10小题,每小题5分,共50 分,在每小题给出的四个选项中,只有一项是满足题目要求的。)
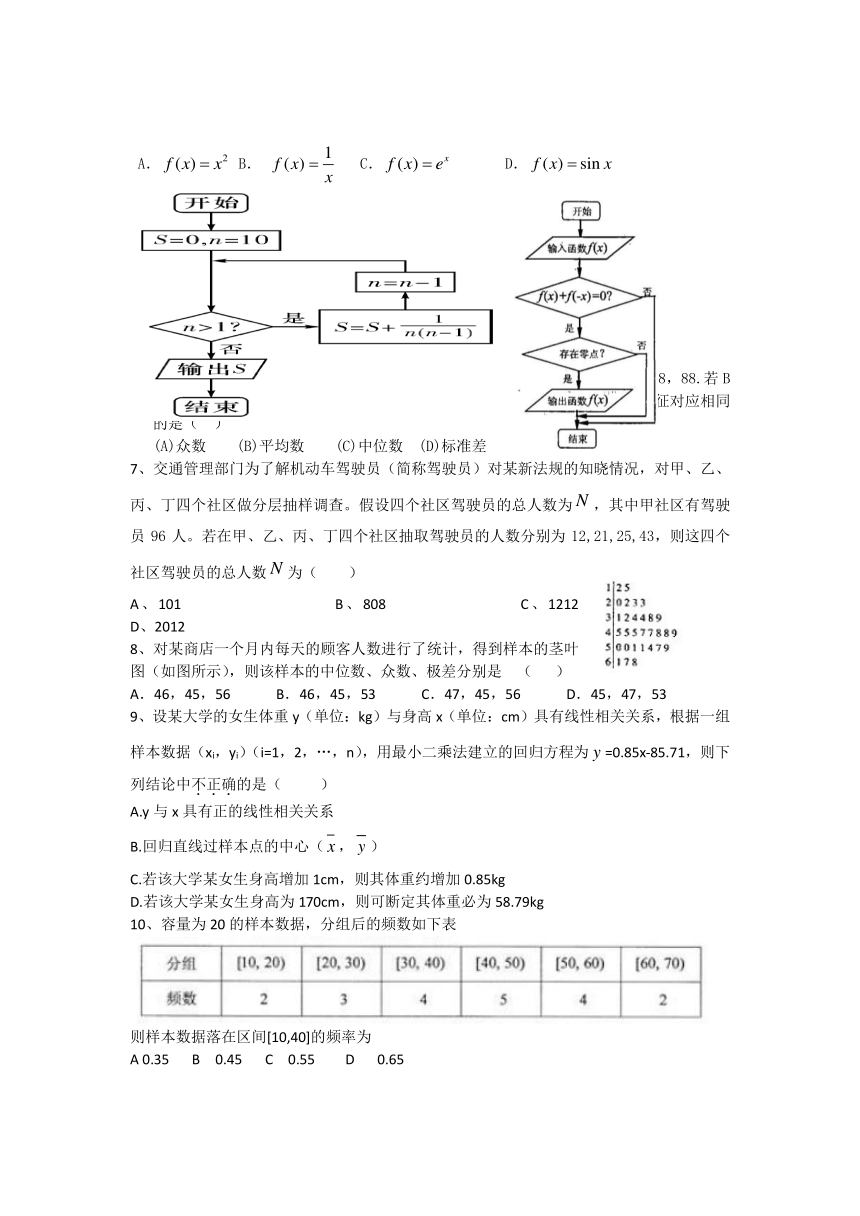
1、如下图所示的程序框图的输出值,则输入值()
A. B.
C. D.
2、阅读下边的程序框图,运行相应的程序,输出的结果为( )
A. B. C. D.
3、读下面的程序框图,若输出的值为,则判断框内空格处可填写( )
A、 B、 C、 D、
4、执行下面的程序框图,输出的S 值为
A. B. C. D.
5、 某程序框图如图所示,现输入如下四个函数,则可以输出的函数是 ( )
A. B. C. D.
6、在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
(A)众数 (B)平均数 (C)中位数 (D)标准差
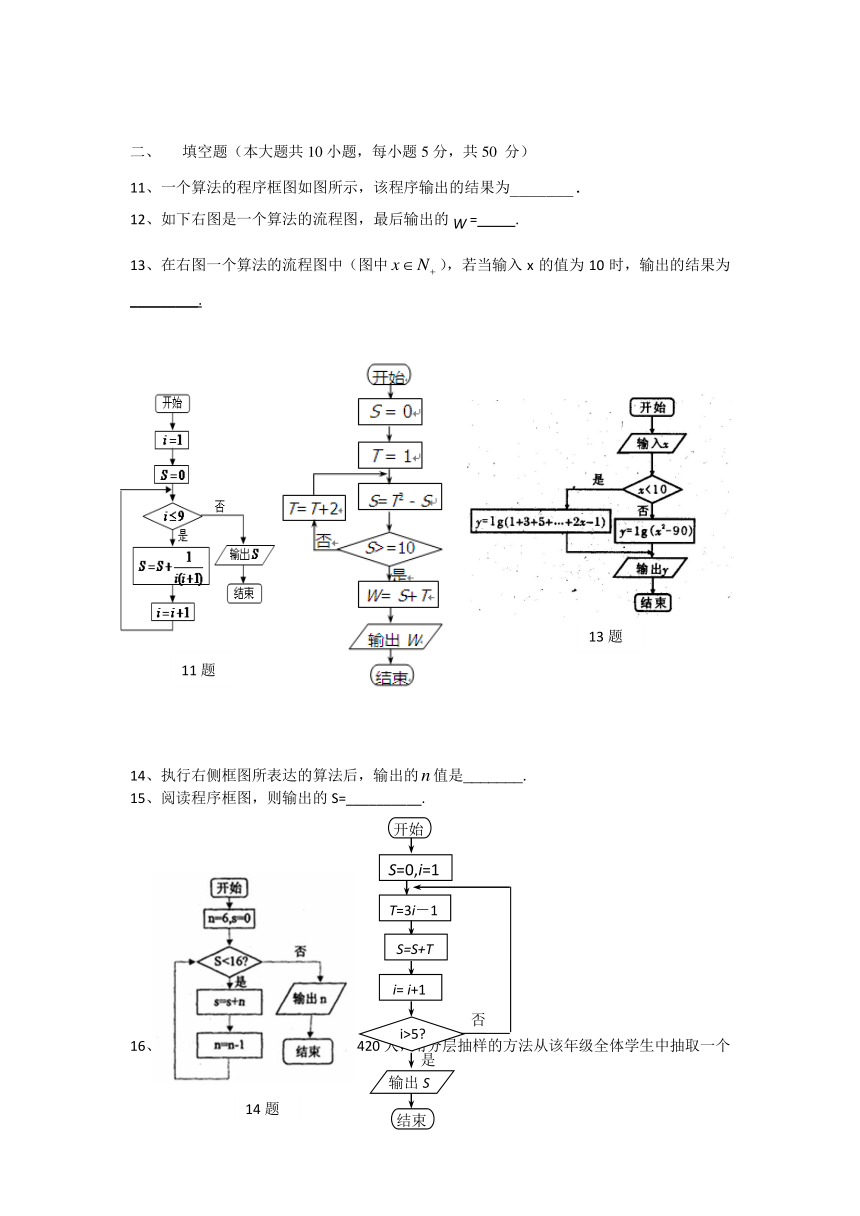
7、交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查。假设四个社区驾驶员的总人数为,其中甲社区有驾驶员96人。若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数为( )
A、101 B、808 C、1212 D、2012
8、对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是 ( )
A.46,45,56 B.46,45,53 C.47,45,56 D.45,47,53
9、设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,则下列结论中不正确的是( )
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心(,)
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
10、容量为20的样本数据,分组后的频数如下表
则样本数据落在区间[10,40]的频率为
A 0.35 B 0.45 C 0.55 D 0.65
填空题(本大题共10小题,每小题5分,共50 分)
11、一个算法的程序框图如图所示,该程序输出的结果为_______.
12、如下右图是一个算法的流程图,最后输出的W = .
13、在右图一个算法的流程图中(图中),若当输入x的值为10时,输出的结果为 _________.
14、执行右侧框图所表达的算法后,输出的值是_______.
15、阅读程序框图,则输出的S=__________.
16、某个年级有男生560人,女生420人,用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本,则此样本中男生人数为____________.
17、下图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为_________.
18、下图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为,,,,,.已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为____.
19、一支田径运动队有男运动员56人,女运动员42人。现用分层抽样的方法抽取若干人,若抽取的男运动员有8人,则抽取的女运动员有______人。
20、由正整数组成的一组数据,其平均数和中位数都是,且标准差等于,则这组数据为 .(从小到大排列)
解答题(本大题共4小题,共50 分)
21(本题满分12分)、某校100名学生期中考试语文成绩的频率分布直方图如图4所示,其中成绩分组区间是:,,,,.
(1)求图中的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数()与数学成绩相应分数段的人数()之比如下表所示,求数学成绩在之外的人数.
分数段
22(本题满分12分)、某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(I)求回归直线方程=bx+a,其中b=-20,a=-b;
(II)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
23(本题满分12分)、如图,在三棱锥中,,,,点在平面内的射影在上。
(Ⅰ)求直线与平面所成的角的大小;
(Ⅱ)求二面角的正切值。
24(本题满分14分)、已知圆的圆心在坐标原点,且恰好与直线相切.
(Ⅰ) 求圆的标准方程;
(Ⅱ)设点为圆上任意一点,轴于,若动点满足
,(其中为常数),试求动点的轨迹方程;
(Ⅲ)在(Ⅱ)的结论下,当时,得到曲线,问是否存在与垂直的一条直线与曲线交于、两点,且为钝角,请说明理由.
高二数学
选择题(本大题共10小题,每小题5分,共50 分,在每小题给出的四个选项中,只有一项是满足题目要求的。)
1、如下图所示的程序框图的输出值,则输入值()
A. B.
C. D.
2、阅读下边的程序框图,运行相应的程序,输出的结果为( )
A. B. C. D.
3、读下面的程序框图,若输出的值为,则判断框内空格处可填写( )
A、 B、 C、 D、
4、执行下面的程序框图,输出的S 值为
A. B. C. D.
5、 某程序框图如图所示,现输入如下四个函数,则可以输出的函数是 ( )
A. B. C. D.
6、在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是( )
(A)众数 (B)平均数 (C)中位数 (D)标准差
7、交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查。假设四个社区驾驶员的总人数为,其中甲社区有驾驶员96人。若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数为( )
A、101 B、808 C、1212 D、2012
8、对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是 ( )
A.46,45,56 B.46,45,53 C.47,45,56 D.45,47,53
9、设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,则下列结论中不正确的是( )
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心(,)
C.若该大学某女生身高增加1cm,则其体重约增加0.85kg
D.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
10、容量为20的样本数据,分组后的频数如下表
则样本数据落在区间[10,40]的频率为
A 0.35 B 0.45 C 0.55 D 0.65
填空题(本大题共10小题,每小题5分,共50 分)
11、一个算法的程序框图如图所示,该程序输出的结果为_______.
12、如下右图是一个算法的流程图,最后输出的W = .
13、在右图一个算法的流程图中(图中),若当输入x的值为10时,输出的结果为 _________.
14、执行右侧框图所表达的算法后,输出的值是_______.
15、阅读程序框图,则输出的S=__________.
16、某个年级有男生560人,女生420人,用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本,则此样本中男生人数为____________.
17、下图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为_________.
18、下图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为,,,,,.已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为____.
19、一支田径运动队有男运动员56人,女运动员42人。现用分层抽样的方法抽取若干人,若抽取的男运动员有8人,则抽取的女运动员有______人。
20、由正整数组成的一组数据,其平均数和中位数都是,且标准差等于,则这组数据为 .(从小到大排列)
解答题(本大题共4小题,共50 分)
21(本题满分12分)、某校100名学生期中考试语文成绩的频率分布直方图如图4所示,其中成绩分组区间是:,,,,.
(1)求图中的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数()与数学成绩相应分数段的人数()之比如下表所示,求数学成绩在之外的人数.
分数段
22(本题满分12分)、某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(I)求回归直线方程=bx+a,其中b=-20,a=-b;
(II)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
23(本题满分12分)、如图,在三棱锥中,,,,点在平面内的射影在上。
(Ⅰ)求直线与平面所成的角的大小;
(Ⅱ)求二面角的正切值。
24(本题满分14分)、已知圆的圆心在坐标原点,且恰好与直线相切.
(Ⅰ) 求圆的标准方程;
(Ⅱ)设点为圆上任意一点,轴于,若动点满足
,(其中为常数),试求动点的轨迹方程;
(Ⅲ)在(Ⅱ)的结论下,当时,得到曲线,问是否存在与垂直的一条直线与曲线交于、两点,且为钝角,请说明理由.
同课章节目录
