2021-2022鲁教版数学八年级上学期 期末模拟测试题(word版含解析)
文档属性
| 名称 | 2021-2022鲁教版数学八年级上学期 期末模拟测试题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 208.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 19:26:47 | ||
图片预览




文档简介
2021-2022鲁教版数学八年级上学期期末模拟测试题
一、选择题
以下四个商标中,是轴对称图形,但不是中心对称图形的是
A. B. C. D.
已知样本数据,,,,,下列说法不正确的是
A. 平均数是 B. 众数是 C. 中位数是 D. 方差是
把代数式分解因式,结果正确的是
A. B. C. D.
若一个正多边形的一个内角是,则这个多边形是
A. 正七边形 B. 正八边形 C. 正九边形 D. 正十边形
若代数式有意义,则实数的取值范围是
A. B. C. D.
小华早上从家出发到离家千米的国际会展中心参观,实际每小时比原计划多走千米,结果比原计划早到了分钟,设小华原计划每小时行千米,可列方程
A. B. C. D.
某青少年篮球队有名队员,队员的年龄情况统计如下表,则这名队员年龄的众数和中位数分别是
年龄岁
人数
A. 岁和岁 B. 岁和岁 C. 岁和岁 D. 岁和岁
如图,在中,,,,将绕点按逆时针旋转得到连接,则的长为
A.
B.
C.
D.
如图,在平行四边形中,平分,交于点,平分,交于点,,,则长为
A.
B.
C.
D.
多项式各项的公因式是
A. B. C. D.
如图,中,,,,由绕点顺时针旋转得到,其中点与点是对应点,点与点是对应点,恰好,,在同一条直线上,交的延长线于点,则的长为
A.
B.
C.
D.
某工地调来人参加挖土和运土,已知人挖出的土人恰好能全部运走,怎样调配劳动力才使挖出来的土能及时运走且不窝工停工等待?为解决此问题,可设派人挖土,其他人运土,下列所列方程:
;;;正确的个数有
A. 个 B. 个 C. 个 D. 个
二、填空题
因式分解:______.
已知,,,,,以此类推,则的值为______.
省运会举行射击比赛,我市射击队从甲、乙、丙、丁四人中选拔一人参赛,在选拔赛中,每人射击次,计算他们次成绩的平均数和方差如下表,请你根据表中数据选一人参加比赛,最适合的人选是______.
甲 乙 丙 丁
平均数
方差
若点与点关于原点成中心对称,则的值是______.
如图,在中,点、分别是边,的中点.若的周长是,则的周长是
如图,四边形是平行四边形,若,则__________.
三、计算题
分解因式:
;
.
解分式方程:
;
.
四、解答题
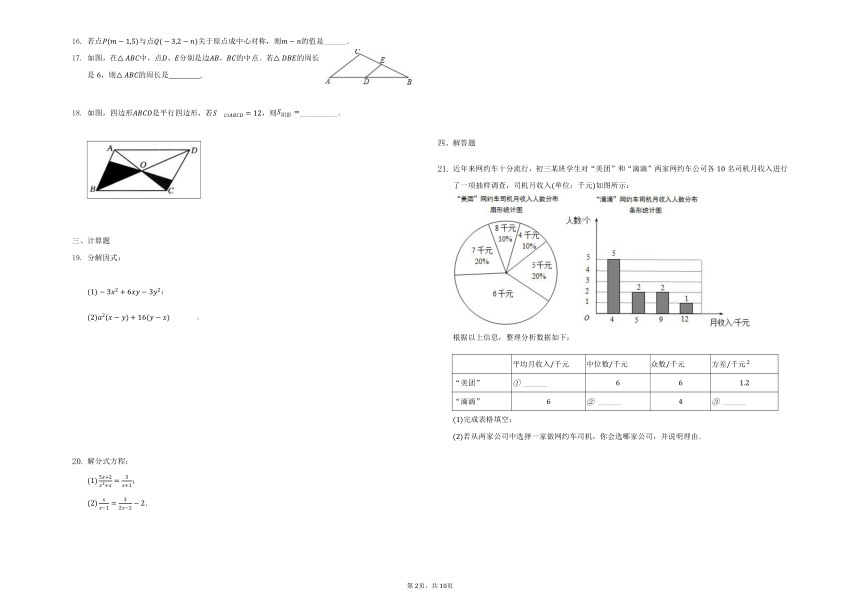
近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各名司机月收入进行了一项抽样调查,司机月收入单位:千元如图所示:
根据以上信息,整理分析数据如下:
平均月收入千元 中位数千元 众数千元 方差千元
“美团” ______
“滴滴” ______ ______
完成表格填空;
若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
如图,三个顶点的坐标分别为,,.
请在图中画出将向左平移个单位长度后得到的图形;
请在图中画出关于轴的对称图形;
请在图中的轴上找一点,使的值最小,并直接写出点的坐标.
如图,中,,将绕点顺时针旋转得到,使得点的对应点落在边上点不与点重合,连接.
依题意补全图形;
求证:四边形是平行四边形.
倡导健康生活推进全民健身,某社区去年购进,两种健身器材若干件,经了解,种健身器材的单价是种健身器材的倍,用元购买种健身器材比用元购买种健身器材多件.
,两种健身器材的单价分别是多少元?
若今年两种健身器材的单价和去年保持不变,该社区计划再购进,两种健身器材共件,且费用不超过元,请问:种健身器材至少要购买多少件?
在中,,,将绕点顺时针旋转一定的角度得到,点、的对应点分别是、.
当点恰好在上时,如图,求的大小;
若时,点是边中点,如图,求证:四边形是平行四边形.
答案和解析
1.【答案】
【解析】解:、是轴对称图形,也是中心对称图形;
B、不是轴对称图形,不是中心对称图形;
C、不是轴对称图形,不是中心对称图形;
D、是轴对称图形,不是中心对称图形.
故选:.
根据轴对称图形与中心对称图形的概念判断.
本题考查的是中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转度后两部分重合.
2.【答案】
【解析】解:样本数据,,,,中平均数是,中位数是,众数是,
方差是.
故选:.
根据众数、中位数、平均数、方差的定义和计算公式分别进行分析即可.
本题考查方差、众数、中位数、平均数.关键是掌握各种数的定义,熟练记住方差公式是解题的关键.
3.【答案】
【解析】解:,
故选:.
首先提取公因式,进而利用平方差公式分解因式得出答案.
此题主要考查了提取公因式法以及公式法分解因式,正确应用公式是解题关键.
4.【答案】
【解析】解:正多边形的一个内角是,
它的外角是:,
边数.
故选:.
首先根据求出外角度数,再利用外角和定理求出边数.
此题主要考查了多边形的外角与内角,做此类题目,首先求出正多边形的外角度数,再利用外角和定理求出求边数.
5.【答案】
【解析】
【分析】
此题主要考查了分式有意义的条件,关键是掌握分式有意义的条件是分母不等于零.
根据分式有意义的条件可得,再解即可.
【解答】
解:由题意得:,
解得:,
故选C.
6.【答案】
【解析】
【分析】
此题考查了由实际问题抽象出分式方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程设小华原计划每小时行千米,则实际每小时走千米,根据结果比原计划早到了分钟列出分式方程即可.
【解答】
解:设小华原计划每小时行千米,则实际每小时走千米,由题意得:
,
故选B.
7.【答案】
【解析】解:在这名队员的年龄数据里,岁出现了次,次数最多,因而众数是岁;
因为共有名队员,第和第个数据的平均数是岁,
因而中位数是岁.
故选:.
根据众数和中位数的定义求解即可.
本题考查了众数和中位数的概念:一组数据中出现次数最多的数据叫做众数;注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
8.【答案】
【解析】解:根据旋转的定义和性质可得,,.
所以.
所以在中,利用勾股定理可得.
故选:.
根据旋转的定义和性质可得,在中利用勾股定理可求的值.
本题主要考查了旋转的性质、勾股定理,解决旋转问题关键要找准旋转角,并弄清旋转后的对应边和对应角.
9.【答案】
【解析】
【分析】
本题主要考查了平行四边形的性质、等腰三角形的判定和性质;熟练掌握平行四边形的性质,证出、是解决问题的关键.
由平行四边形的性质和角平分线得出,得出,同理可证,再由的长可得,,即可求出的长.
【解答】
解:四边形是平行四边形,
,,,
,
平分,
,
则,
,
同理可证:,
,
即,
解得:,
.
10.【答案】
【解析】分别找出公因式的系数、字母及次数,得
11.【答案】
【解析】
【分析】
本题考查了旋转的性质,掌握对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等是本题的关键.解题时注意:在直角三角形
中,角所对的直角边等于斜边的一半.
先根据中,,,,求得,再根据旋转的性质,求得,最后在中,根据勾股定理即可得到的长.
【解答】
解:,,
,
,
,,
绕点顺时针旋转得到,
,,,
为等腰三角形,
,
A、、在同一条直线上,
,
,
,
又,
,
中,,
,
故选C.
12.【答案】
【解析】解:人挖土,则运土,人挖出的土人恰好能全部运走,那么使挖出来的土能及时运走且不窝工,说明挖土的人的数量与运土人的数量之比:都是这个等量关系的变形正确.运土的人数应是,方程应为,
故选:.
关键描述语为:“人挖出的土人恰好能全部运走”;等量关系为:挖土的人的数量与运土人的数量之比:,由此列式.
找到关键描述语,找到等量关系是解决问题的关键.本题需重点理解:人挖出的土人恰好能全部运走.
13.【答案】
【解析】解:原式;
故答案为:.
原式提取,再运用完全平方公式分解即可.
此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
14.【答案】
【解析】解:,
,
,
;
,
每个的值循环一轮,
,
和的值相等为.
故答案为:.
直接根据计算公式分别得出的值,进而得出规律求出答案.
此题主要考查了数字变化规律,正确得出变化规律是解题关键.
15.【答案】丁
【解析】解:甲,乙,丙,丁四个人中甲和丁的平均数最大且相等,
甲,乙,丙,丁四个人中丁的方差最小,
说明丁的成绩最稳定,
综合平均数和方差两个方面说明丁成绩既高又稳定,
丁是最佳人选.
故答案为:丁.
根据甲,乙,丙,丁四个人中甲和丁的平均数最大且相等,甲,乙,丙,丁四个人中丁的方差最小,说明丁的成绩最稳定,得到丁是最佳人选.
本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
16.【答案】
【解析】解:点与点关于原点成中心对称,
,,
解得,,
则的值为,
故答案:.
直接利用关于原点对称点的性质得出,的值,进而得出答案.
此题主要考查了关于原点对称点的性质,关于原点对称的点,横坐标与纵坐标都互为相反数.正确得出,的值是解题的关键.
17.【答案】
【解析】
【分析】
此题主要考查了三角形中位线定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的中位线平行于第三边,并且等于第三边的一半.此题还考查了三角形的周长和含义的求法,要熟练掌握.首先根据点、分别是边,的中点,可得是三角形的中位线,然后根据三角形中位线定理,可得,最后根据三角形周长的含义,判断出的周长和的周长的关系,再结合的周长是,即可求出的周长是多少.
【解答】
解:点、分别是边,的中点,
是三角形的中位线,,,
且,
又,,
,
即的周长是的周长的倍,
的周长是,
的周长是:.
故答案为.
18.【答案】
【解析】
【分析】
本题考查平行四边形的性质,全等三角形的判定和性质,根据平行四边形的性质得出,,进而得出三角形的面积相等,从而得出结论即可.
【解答】
解:如图:
四边形是平行四边形,
,,
,
,
,
,,
≌,
,
.
故答案为.
19.【答案】解:原式
;
原式
.
【解析】本题考查了提公因式法与公式法分解因式.
提取公因式,然后利用完全平方差公式进行分解;
首先提取公因式,然后利用平方差公式进行因式分解,整理即可.
20.【答案】解:方程两边都乘以得:,
解得:,
检验:当时,,
所以是增根,
即原方程无解;
方程两边都乘以得:,
解得:,
检验:当时,,
所以是原方程的解,
即原方程的解是:.
【解析】本题考查了解分式方程,能把分式方程转化成整式方程是解此题的关键.
方程两边都乘以得出,求出方程的解,再进行检验即可;
方程两边都乘以得出,求出方程的解,再进行检验即可.
21.【答案】解:;;;
选美团,因为平均数一样,中位数、众数美团大于滴滴,且美团方差小,更稳定.
【解析】
解:美团平均月收入:;
滴滴中位数为;
方差:;
故答案为:;;;
见答案.
【分析】
利用平均数、中位数、众数及方差的定义分别计算后即可确定正确的答案;
根据平均数一样,中位数及众数的大小和方差的大小进行选择即可.
本题考查了统计的有关知识,解题的关键是能够了解有关的计算公式,难度不大.
22.【答案】解:如图所示:,即为所求;
如图所示:,即为所求;
如图所示:点,使的值最小,点的坐标为:.
【解析】直接利用平移的性质得出对应点位置进而得出答案;
直接利用关于轴对称点的性质得出对应点位置进而得出答案;
利用轴对称求最短路线的方法分析得出答案.
此题主要考查了轴对称变换以及平移变换、利用轴对称求最短路径,正确得出对应点位置是解题关键.
23.【答案】解:如图所示:
绕点顺时针旋转得到,
≌,,,
,
,
≌,
,
,
,
,
,
,
,
又,,
四边形是平行四边形.
【解析】根据题目要求作图即可得;
先证,得,据此知,结合,可得.
本题主要考查作图旋转变换,解题的关键是掌握旋转变换的定义和性质、平行四边形的判定及全等三角形的性质等知识点.
24.【答案】解:设种型号健身器材的单价为元套,种型号健身器材的单价为元套,
根据题意,可得:,
解得:,
经检验是原方程的根,
元,
因此,,两种健身器材的单价分别是元,元;
设购买种型号健身器材套,则购买种型号的健身器材套,
根据题意,可得:,
解得:,
因此,种型号健身器材至少购买套.
【解析】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:找准等量关系,正确列出分式方程;根据各数量之间的关系,正确列出一元一次不等式.
设种型号健身器材的单价为元套,种型号健身器材的单价为元套,根据“用元购买种健身器材比用元购买种健身器材多件”,即可得出关于的分式方程,解之即可得出结论;
设购买种型号健身器材套,则购买种型号的健身器材套,根据总价单价数量结合这次购买两种健身器材的总费用不超过元,即可得出关于的一元一次不等式,解之取其最小值即可得出结论.
25.【答案】解:如图,
绕点顺时针旋转得到,点恰好在上,
,,,
,
,
;
证明:连接,如图,
点是边中点,
,
,,
,
,
绕点顺时针旋转得到,
,,,
,和为等边三角形,
,
点为的边的中点,
,
则,,,
≌,
,
,
而,
四边形是平行四边形.
【解析】本题考查了旋转的性质:对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的判定.
如图,利用旋转的性质得,,,再根据等腰三角形的性质和三角形内角和计算出,从而利用互余计算出的度数;
如图,利用直角三角形斜边上的中线性质得到,利用含度的直角三角形三边的关系得到,则,再根据旋转的性质得到,,,从而得到,和为等边三角形,接着证明≌得到,然后根据平行四边形的判定方法得到结论.
第2页,共2页
第1页,共1页
一、选择题
以下四个商标中,是轴对称图形,但不是中心对称图形的是
A. B. C. D.
已知样本数据,,,,,下列说法不正确的是
A. 平均数是 B. 众数是 C. 中位数是 D. 方差是
把代数式分解因式,结果正确的是
A. B. C. D.
若一个正多边形的一个内角是,则这个多边形是
A. 正七边形 B. 正八边形 C. 正九边形 D. 正十边形
若代数式有意义,则实数的取值范围是
A. B. C. D.
小华早上从家出发到离家千米的国际会展中心参观,实际每小时比原计划多走千米,结果比原计划早到了分钟,设小华原计划每小时行千米,可列方程
A. B. C. D.
某青少年篮球队有名队员,队员的年龄情况统计如下表,则这名队员年龄的众数和中位数分别是
年龄岁
人数
A. 岁和岁 B. 岁和岁 C. 岁和岁 D. 岁和岁
如图,在中,,,,将绕点按逆时针旋转得到连接,则的长为
A.
B.
C.
D.
如图,在平行四边形中,平分,交于点,平分,交于点,,,则长为
A.
B.
C.
D.
多项式各项的公因式是
A. B. C. D.
如图,中,,,,由绕点顺时针旋转得到,其中点与点是对应点,点与点是对应点,恰好,,在同一条直线上,交的延长线于点,则的长为
A.
B.
C.
D.
某工地调来人参加挖土和运土,已知人挖出的土人恰好能全部运走,怎样调配劳动力才使挖出来的土能及时运走且不窝工停工等待?为解决此问题,可设派人挖土,其他人运土,下列所列方程:
;;;正确的个数有
A. 个 B. 个 C. 个 D. 个
二、填空题
因式分解:______.
已知,,,,,以此类推,则的值为______.
省运会举行射击比赛,我市射击队从甲、乙、丙、丁四人中选拔一人参赛,在选拔赛中,每人射击次,计算他们次成绩的平均数和方差如下表,请你根据表中数据选一人参加比赛,最适合的人选是______.
甲 乙 丙 丁
平均数
方差
若点与点关于原点成中心对称,则的值是______.
如图,在中,点、分别是边,的中点.若的周长是,则的周长是
如图,四边形是平行四边形,若,则__________.
三、计算题
分解因式:
;
.
解分式方程:
;
.
四、解答题
近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各名司机月收入进行了一项抽样调查,司机月收入单位:千元如图所示:
根据以上信息,整理分析数据如下:
平均月收入千元 中位数千元 众数千元 方差千元
“美团” ______
“滴滴” ______ ______
完成表格填空;
若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.
如图,三个顶点的坐标分别为,,.
请在图中画出将向左平移个单位长度后得到的图形;
请在图中画出关于轴的对称图形;
请在图中的轴上找一点,使的值最小,并直接写出点的坐标.
如图,中,,将绕点顺时针旋转得到,使得点的对应点落在边上点不与点重合,连接.
依题意补全图形;
求证:四边形是平行四边形.
倡导健康生活推进全民健身,某社区去年购进,两种健身器材若干件,经了解,种健身器材的单价是种健身器材的倍,用元购买种健身器材比用元购买种健身器材多件.
,两种健身器材的单价分别是多少元?
若今年两种健身器材的单价和去年保持不变,该社区计划再购进,两种健身器材共件,且费用不超过元,请问:种健身器材至少要购买多少件?
在中,,,将绕点顺时针旋转一定的角度得到,点、的对应点分别是、.
当点恰好在上时,如图,求的大小;
若时,点是边中点,如图,求证:四边形是平行四边形.
答案和解析
1.【答案】
【解析】解:、是轴对称图形,也是中心对称图形;
B、不是轴对称图形,不是中心对称图形;
C、不是轴对称图形,不是中心对称图形;
D、是轴对称图形,不是中心对称图形.
故选:.
根据轴对称图形与中心对称图形的概念判断.
本题考查的是中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转度后两部分重合.
2.【答案】
【解析】解:样本数据,,,,中平均数是,中位数是,众数是,
方差是.
故选:.
根据众数、中位数、平均数、方差的定义和计算公式分别进行分析即可.
本题考查方差、众数、中位数、平均数.关键是掌握各种数的定义,熟练记住方差公式是解题的关键.
3.【答案】
【解析】解:,
故选:.
首先提取公因式,进而利用平方差公式分解因式得出答案.
此题主要考查了提取公因式法以及公式法分解因式,正确应用公式是解题关键.
4.【答案】
【解析】解:正多边形的一个内角是,
它的外角是:,
边数.
故选:.
首先根据求出外角度数,再利用外角和定理求出边数.
此题主要考查了多边形的外角与内角,做此类题目,首先求出正多边形的外角度数,再利用外角和定理求出求边数.
5.【答案】
【解析】
【分析】
此题主要考查了分式有意义的条件,关键是掌握分式有意义的条件是分母不等于零.
根据分式有意义的条件可得,再解即可.
【解答】
解:由题意得:,
解得:,
故选C.
6.【答案】
【解析】
【分析】
此题考查了由实际问题抽象出分式方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程设小华原计划每小时行千米,则实际每小时走千米,根据结果比原计划早到了分钟列出分式方程即可.
【解答】
解:设小华原计划每小时行千米,则实际每小时走千米,由题意得:
,
故选B.
7.【答案】
【解析】解:在这名队员的年龄数据里,岁出现了次,次数最多,因而众数是岁;
因为共有名队员,第和第个数据的平均数是岁,
因而中位数是岁.
故选:.
根据众数和中位数的定义求解即可.
本题考查了众数和中位数的概念:一组数据中出现次数最多的数据叫做众数;注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
8.【答案】
【解析】解:根据旋转的定义和性质可得,,.
所以.
所以在中,利用勾股定理可得.
故选:.
根据旋转的定义和性质可得,在中利用勾股定理可求的值.
本题主要考查了旋转的性质、勾股定理,解决旋转问题关键要找准旋转角,并弄清旋转后的对应边和对应角.
9.【答案】
【解析】
【分析】
本题主要考查了平行四边形的性质、等腰三角形的判定和性质;熟练掌握平行四边形的性质,证出、是解决问题的关键.
由平行四边形的性质和角平分线得出,得出,同理可证,再由的长可得,,即可求出的长.
【解答】
解:四边形是平行四边形,
,,,
,
平分,
,
则,
,
同理可证:,
,
即,
解得:,
.
10.【答案】
【解析】分别找出公因式的系数、字母及次数,得
11.【答案】
【解析】
【分析】
本题考查了旋转的性质,掌握对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等是本题的关键.解题时注意:在直角三角形
中,角所对的直角边等于斜边的一半.
先根据中,,,,求得,再根据旋转的性质,求得,最后在中,根据勾股定理即可得到的长.
【解答】
解:,,
,
,
,,
绕点顺时针旋转得到,
,,,
为等腰三角形,
,
A、、在同一条直线上,
,
,
,
又,
,
中,,
,
故选C.
12.【答案】
【解析】解:人挖土,则运土,人挖出的土人恰好能全部运走,那么使挖出来的土能及时运走且不窝工,说明挖土的人的数量与运土人的数量之比:都是这个等量关系的变形正确.运土的人数应是,方程应为,
故选:.
关键描述语为:“人挖出的土人恰好能全部运走”;等量关系为:挖土的人的数量与运土人的数量之比:,由此列式.
找到关键描述语,找到等量关系是解决问题的关键.本题需重点理解:人挖出的土人恰好能全部运走.
13.【答案】
【解析】解:原式;
故答案为:.
原式提取,再运用完全平方公式分解即可.
此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
14.【答案】
【解析】解:,
,
,
;
,
每个的值循环一轮,
,
和的值相等为.
故答案为:.
直接根据计算公式分别得出的值,进而得出规律求出答案.
此题主要考查了数字变化规律,正确得出变化规律是解题关键.
15.【答案】丁
【解析】解:甲,乙,丙,丁四个人中甲和丁的平均数最大且相等,
甲,乙,丙,丁四个人中丁的方差最小,
说明丁的成绩最稳定,
综合平均数和方差两个方面说明丁成绩既高又稳定,
丁是最佳人选.
故答案为:丁.
根据甲,乙,丙,丁四个人中甲和丁的平均数最大且相等,甲,乙,丙,丁四个人中丁的方差最小,说明丁的成绩最稳定,得到丁是最佳人选.
本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
16.【答案】
【解析】解:点与点关于原点成中心对称,
,,
解得,,
则的值为,
故答案:.
直接利用关于原点对称点的性质得出,的值,进而得出答案.
此题主要考查了关于原点对称点的性质,关于原点对称的点,横坐标与纵坐标都互为相反数.正确得出,的值是解题的关键.
17.【答案】
【解析】
【分析】
此题主要考查了三角形中位线定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的中位线平行于第三边,并且等于第三边的一半.此题还考查了三角形的周长和含义的求法,要熟练掌握.首先根据点、分别是边,的中点,可得是三角形的中位线,然后根据三角形中位线定理,可得,最后根据三角形周长的含义,判断出的周长和的周长的关系,再结合的周长是,即可求出的周长是多少.
【解答】
解:点、分别是边,的中点,
是三角形的中位线,,,
且,
又,,
,
即的周长是的周长的倍,
的周长是,
的周长是:.
故答案为.
18.【答案】
【解析】
【分析】
本题考查平行四边形的性质,全等三角形的判定和性质,根据平行四边形的性质得出,,进而得出三角形的面积相等,从而得出结论即可.
【解答】
解:如图:
四边形是平行四边形,
,,
,
,
,
,,
≌,
,
.
故答案为.
19.【答案】解:原式
;
原式
.
【解析】本题考查了提公因式法与公式法分解因式.
提取公因式,然后利用完全平方差公式进行分解;
首先提取公因式,然后利用平方差公式进行因式分解,整理即可.
20.【答案】解:方程两边都乘以得:,
解得:,
检验:当时,,
所以是增根,
即原方程无解;
方程两边都乘以得:,
解得:,
检验:当时,,
所以是原方程的解,
即原方程的解是:.
【解析】本题考查了解分式方程,能把分式方程转化成整式方程是解此题的关键.
方程两边都乘以得出,求出方程的解,再进行检验即可;
方程两边都乘以得出,求出方程的解,再进行检验即可.
21.【答案】解:;;;
选美团,因为平均数一样,中位数、众数美团大于滴滴,且美团方差小,更稳定.
【解析】
解:美团平均月收入:;
滴滴中位数为;
方差:;
故答案为:;;;
见答案.
【分析】
利用平均数、中位数、众数及方差的定义分别计算后即可确定正确的答案;
根据平均数一样,中位数及众数的大小和方差的大小进行选择即可.
本题考查了统计的有关知识,解题的关键是能够了解有关的计算公式,难度不大.
22.【答案】解:如图所示:,即为所求;
如图所示:,即为所求;
如图所示:点,使的值最小,点的坐标为:.
【解析】直接利用平移的性质得出对应点位置进而得出答案;
直接利用关于轴对称点的性质得出对应点位置进而得出答案;
利用轴对称求最短路线的方法分析得出答案.
此题主要考查了轴对称变换以及平移变换、利用轴对称求最短路径,正确得出对应点位置是解题关键.
23.【答案】解:如图所示:
绕点顺时针旋转得到,
≌,,,
,
,
≌,
,
,
,
,
,
,
,
又,,
四边形是平行四边形.
【解析】根据题目要求作图即可得;
先证,得,据此知,结合,可得.
本题主要考查作图旋转变换,解题的关键是掌握旋转变换的定义和性质、平行四边形的判定及全等三角形的性质等知识点.
24.【答案】解:设种型号健身器材的单价为元套,种型号健身器材的单价为元套,
根据题意,可得:,
解得:,
经检验是原方程的根,
元,
因此,,两种健身器材的单价分别是元,元;
设购买种型号健身器材套,则购买种型号的健身器材套,
根据题意,可得:,
解得:,
因此,种型号健身器材至少购买套.
【解析】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:找准等量关系,正确列出分式方程;根据各数量之间的关系,正确列出一元一次不等式.
设种型号健身器材的单价为元套,种型号健身器材的单价为元套,根据“用元购买种健身器材比用元购买种健身器材多件”,即可得出关于的分式方程,解之即可得出结论;
设购买种型号健身器材套,则购买种型号的健身器材套,根据总价单价数量结合这次购买两种健身器材的总费用不超过元,即可得出关于的一元一次不等式,解之取其最小值即可得出结论.
25.【答案】解:如图,
绕点顺时针旋转得到,点恰好在上,
,,,
,
,
;
证明:连接,如图,
点是边中点,
,
,,
,
,
绕点顺时针旋转得到,
,,,
,和为等边三角形,
,
点为的边的中点,
,
则,,,
≌,
,
,
而,
四边形是平行四边形.
【解析】本题考查了旋转的性质:对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的判定.
如图,利用旋转的性质得,,,再根据等腰三角形的性质和三角形内角和计算出,从而利用互余计算出的度数;
如图,利用直角三角形斜边上的中线性质得到,利用含度的直角三角形三边的关系得到,则,再根据旋转的性质得到,,,从而得到,和为等边三角形,接着证明≌得到,然后根据平行四边形的判定方法得到结论.
第2页,共2页
第1页,共1页
同课章节目录
