2021-2022学年湘教版数学九年级下册2.2.2第1课时圆周角定理与推论1课件(共32张PPT)
文档属性
| 名称 | 2021-2022学年湘教版数学九年级下册2.2.2第1课时圆周角定理与推论1课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 547.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 11:57:52 | ||
图片预览









文档简介
(共32张PPT)
2.2 圆心角、圆周角
第2章 圆
第1课时 圆周角定理与推论1
2.2.2 圆周角
学习目标
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.(重点、难点)
3.理解掌握圆周角定理的推论及其证明过程和运用.(难点)
1.圆心角的定义
.
O
B
C
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
答:顶点在圆心的角叫圆心角。
2.上节课我们学习了一个反映圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
O
A
B
如图,已知∠AOB=80°,
①求弧AB的度数;
C
80°
40°
②延长AO交⊙O于点C,连结CB,
求∠C的度数。
O
B
C
·
圆心角的顶点发生变化时,我们得到几种情况:
O
B
C
·
O
B
C
·
A
A
A
圆周角
你能仿照圆心角的定义给圆周角下个定义吗
O
B
C
·
A
顶点在圆上,并且两边都和圆相交的角叫圆周角。
特征:
① 角的顶点在圆上。
② 角的两边都与圆相交。
动脑筋
顶点在圆上,并且两边都与圆相交的角叫作圆周角.
(如∠BAC)
我们把∠BAC叫作BC所对圆周角,BC叫作圆周角∠BAC所对的弧.
圆周角的定义
一
⌒
⌒
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
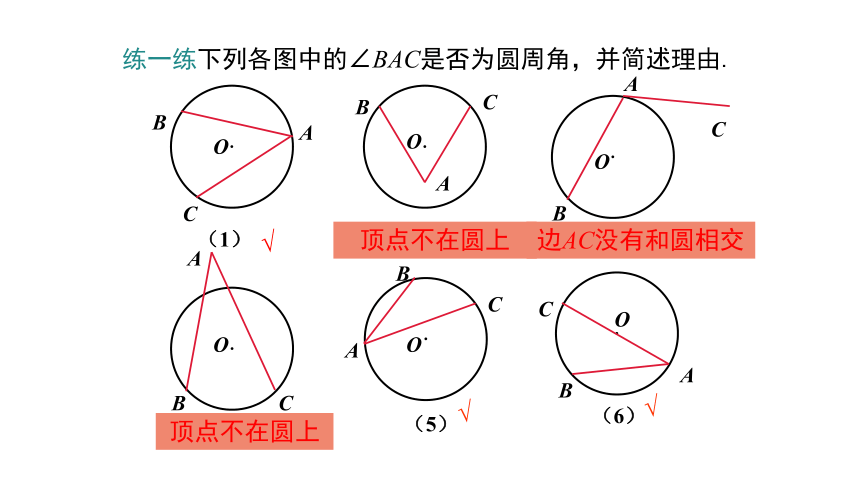
练一练下列各图中的∠BAC是否为圆周角,并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
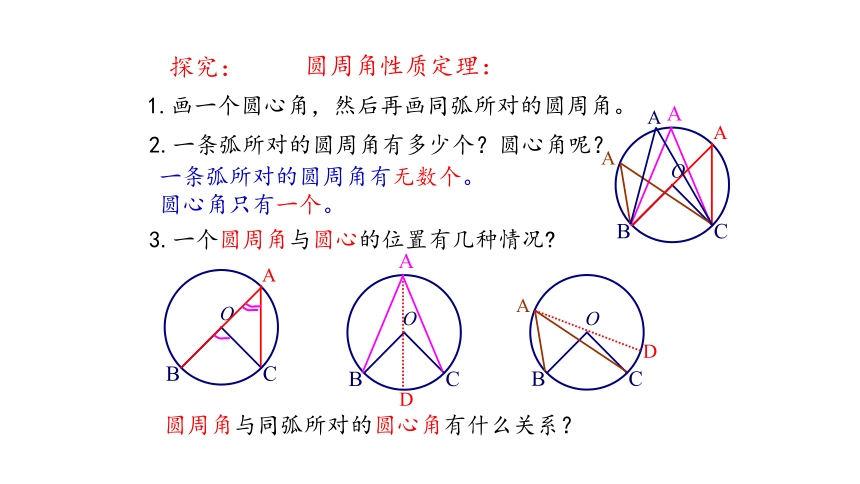
圆周角性质定理:
1.画一个圆心角,然后再画同弧所对的圆周角。
2.一条弧所对的圆周角有多少个?圆心角呢?
一条弧所对的圆周角有无数个。
圆心角只有一个。
3.一个圆周角与圆心的位置有几种情况
O
B
C
·
A
A
A
A
O
B
C
·
A
O
B
C
·
A
O
B
C
·
A
圆周角与同弧所对的圆心角有什么关系?
D
D
探究:
推导与验证
已知:在圆O中,弧BC所对的圆周角是∠BAC,圆心角是∠BOC.
求证:∠BAC= ∠BOC.
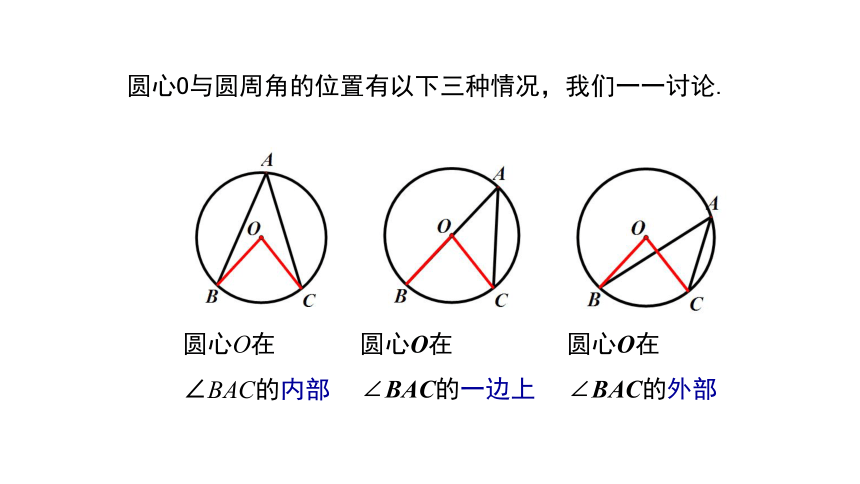
圆心O在∠BAC的内部
圆心O在
∠BAC的一边上
圆心O在
∠BAC的外部
圆心O与圆周角的位置有以下三种情况,我们一一讨论.
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
O
A
B
D
O
A
C
D
O
A
B
C
D
圆心O在∠BAC的内部
C
O
A
B
D
圆心O在∠BAC的外部
圆周角的度数等于它所对弧上的圆心角度数的一半.
圆周角定理
知识要点
·
·
·
100°
A
O
20°
O
90°
A
B
A
B
B
C
C
(1)
(2)
(3)
求∠AOB
求∠AOB
求∠A
练一练
1.
解:∵圆心角∠AOB 与圆周角∠ACB
所对的弧为 ,
例1 如图,OA,OB,OC都是⊙O的半径,∠AOB=50°,∠BOC=70°.求∠ACB和∠BAC度数.
AB
⌒
B
C
O
.
70°
A
∴∠ACB= ∠AOB=25°.
同理∠BAC= ∠BOC=35°.
典例精析
例2 如图,AB是⊙O的直径,C、D、E是⊙O上的点,则∠1+∠2等于( )
A.90° B.45° C.180° D.60°
A
例3 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15°
C.20° D.22.5°
解析:连接OB,
∵四边形ABCO是平行四边形,
∴OC=AB,又OA=OB=OC,
∴OA=OB=AB,
∴△AOB为等边三角形,
∵OF⊥OC,OC∥AB,
∴OF⊥AB,
∴∠BOF=∠AOF=30°,
由圆周角定理得∠BAF= ∠BOF=15°,
故选:B.
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC。这三个角的大小有什么关系
B
A
C
D
E
E
●O
B
D
C
A
你能发现什么规律?
AC所对的圆周角∠AEC, ∠ABC ,∠ADC的大小有什么关系?
⌒
实践活动
圆周角定理的推论1
三
要点归纳
圆周角定理的推论1
在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
完成下列填空
∠1= .
∠2= .
∠3= .
∠5= .
如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
∠4
∠8
∠6
∠7
A
B
C
D
O
1
(
(
(
(
(
(
(
(
2
3
4
5
6
7
8
练一练
例4 如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15° B.25° C.30° D.75°
典例精析
C
1.判断下列各图形中的角是不是圆周角.
图1
图2
图3
图4
图5
2.指出图中的圆周角.
A
O
B
C
∠ACO ∠ACB ∠BCO ∠OAB ∠BAC ∠OAC ∠ABC
×
×
√
×
×
3.如图,点B,C在⊙O上,且BO=BC,则圆周角∠BAC等于( )
D
A.60°
B.50°
C.40°
D.30°
4.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于( )
A.25°
B.30°C.35°D.50°
A
5.如图,在⊙O中,弧AB=弧AC,∠AOB=50°,则∠ADC的度数是( )
A.50° B.40°
C.30° D.25°
D
6.如图,AB是⊙O的直径,∠AOD是圆心角, ∠BCD是圆周角,若∠BCD=25°,则∠AOD= .
130°
7.如图,已知圆心角∠AOB=100°,则圆周角
∠ACB= ,∠ADB= .
D
A
O
C
B
130°
50°
8.如图,在⊙O中,弧AB=弧CD,∠DCB=28°,则∠ABC=_______°.
28
9.如图,分别求出图中∠x的大小.
解:(1)∵同弧所对圆周角相等,∴∠x=60°.
(2)连接BF,
F
∵同弧所对圆周角相等,
∴∠ABF=∠D=20°,∠FBC=∠E=30°.
∴∠x=∠ABF+∠FBC=50°.
60°
x
30°
20°
x
A
D
B
E
C
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论1
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧(或等弧)所对的圆周角相等;相等的圆周角所对的弧也相等
1.顶点在圆上,2.两边都与圆相交的角
2.2 圆心角、圆周角
第2章 圆
第1课时 圆周角定理与推论1
2.2.2 圆周角
学习目标
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.(重点、难点)
3.理解掌握圆周角定理的推论及其证明过程和运用.(难点)
1.圆心角的定义
.
O
B
C
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
答:顶点在圆心的角叫圆心角。
2.上节课我们学习了一个反映圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
O
A
B
如图,已知∠AOB=80°,
①求弧AB的度数;
C
80°
40°
②延长AO交⊙O于点C,连结CB,
求∠C的度数。
O
B
C
·
圆心角的顶点发生变化时,我们得到几种情况:
O
B
C
·
O
B
C
·
A
A
A
圆周角
你能仿照圆心角的定义给圆周角下个定义吗
O
B
C
·
A
顶点在圆上,并且两边都和圆相交的角叫圆周角。
特征:
① 角的顶点在圆上。
② 角的两边都与圆相交。
动脑筋
顶点在圆上,并且两边都与圆相交的角叫作圆周角.
(如∠BAC)
我们把∠BAC叫作BC所对圆周角,BC叫作圆周角∠BAC所对的弧.
圆周角的定义
一
⌒
⌒
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
练一练下列各图中的∠BAC是否为圆周角,并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
圆周角性质定理:
1.画一个圆心角,然后再画同弧所对的圆周角。
2.一条弧所对的圆周角有多少个?圆心角呢?
一条弧所对的圆周角有无数个。
圆心角只有一个。
3.一个圆周角与圆心的位置有几种情况
O
B
C
·
A
A
A
A
O
B
C
·
A
O
B
C
·
A
O
B
C
·
A
圆周角与同弧所对的圆心角有什么关系?
D
D
探究:
推导与验证
已知:在圆O中,弧BC所对的圆周角是∠BAC,圆心角是∠BOC.
求证:∠BAC= ∠BOC.
圆心O在∠BAC的内部
圆心O在
∠BAC的一边上
圆心O在
∠BAC的外部
圆心O与圆周角的位置有以下三种情况,我们一一讨论.
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
O
A
B
D
O
A
C
D
O
A
B
C
D
圆心O在∠BAC的内部
C
O
A
B
D
圆心O在∠BAC的外部
圆周角的度数等于它所对弧上的圆心角度数的一半.
圆周角定理
知识要点
·
·
·
100°
A
O
20°
O
90°
A
B
A
B
B
C
C
(1)
(2)
(3)
求∠AOB
求∠AOB
求∠A
练一练
1.
解:∵圆心角∠AOB 与圆周角∠ACB
所对的弧为 ,
例1 如图,OA,OB,OC都是⊙O的半径,∠AOB=50°,∠BOC=70°.求∠ACB和∠BAC度数.
AB
⌒
B
C
O
.
70°
A
∴∠ACB= ∠AOB=25°.
同理∠BAC= ∠BOC=35°.
典例精析
例2 如图,AB是⊙O的直径,C、D、E是⊙O上的点,则∠1+∠2等于( )
A.90° B.45° C.180° D.60°
A
例3 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15°
C.20° D.22.5°
解析:连接OB,
∵四边形ABCO是平行四边形,
∴OC=AB,又OA=OB=OC,
∴OA=OB=AB,
∴△AOB为等边三角形,
∵OF⊥OC,OC∥AB,
∴OF⊥AB,
∴∠BOF=∠AOF=30°,
由圆周角定理得∠BAF= ∠BOF=15°,
故选:B.
当球员在B,D,E处射门时,他所处的位置对球门AC分别形成三个张角∠ABC, ∠ADC,∠AEC。这三个角的大小有什么关系
B
A
C
D
E
E
●O
B
D
C
A
你能发现什么规律?
AC所对的圆周角∠AEC, ∠ABC ,∠ADC的大小有什么关系?
⌒
实践活动
圆周角定理的推论1
三
要点归纳
圆周角定理的推论1
在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
完成下列填空
∠1= .
∠2= .
∠3= .
∠5= .
如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线.
∠4
∠8
∠6
∠7
A
B
C
D
O
1
(
(
(
(
(
(
(
(
2
3
4
5
6
7
8
练一练
例4 如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15° B.25° C.30° D.75°
典例精析
C
1.判断下列各图形中的角是不是圆周角.
图1
图2
图3
图4
图5
2.指出图中的圆周角.
A
O
B
C
∠ACO ∠ACB ∠BCO ∠OAB ∠BAC ∠OAC ∠ABC
×
×
√
×
×
3.如图,点B,C在⊙O上,且BO=BC,则圆周角∠BAC等于( )
D
A.60°
B.50°
C.40°
D.30°
4.如图,AB是⊙O的直径,C,D为圆上两点,∠AOC=130°,则∠D等于( )
A.25°
B.30°C.35°D.50°
A
5.如图,在⊙O中,弧AB=弧AC,∠AOB=50°,则∠ADC的度数是( )
A.50° B.40°
C.30° D.25°
D
6.如图,AB是⊙O的直径,∠AOD是圆心角, ∠BCD是圆周角,若∠BCD=25°,则∠AOD= .
130°
7.如图,已知圆心角∠AOB=100°,则圆周角
∠ACB= ,∠ADB= .
D
A
O
C
B
130°
50°
8.如图,在⊙O中,弧AB=弧CD,∠DCB=28°,则∠ABC=_______°.
28
9.如图,分别求出图中∠x的大小.
解:(1)∵同弧所对圆周角相等,∴∠x=60°.
(2)连接BF,
F
∵同弧所对圆周角相等,
∴∠ABF=∠D=20°,∠FBC=∠E=30°.
∴∠x=∠ABF+∠FBC=50°.
60°
x
30°
20°
x
A
D
B
E
C
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论1
一条弧所对的圆周角等于它所对的圆心角的一半.
同弧(或等弧)所对的圆周角相等;相等的圆周角所对的弧也相等
1.顶点在圆上,2.两边都与圆相交的角
