2021-2022学年湖南省郴州市九年级(上)联考数学试卷(12月份)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年湖南省郴州市九年级(上)联考数学试卷(12月份)(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 07:10:37 | ||
图片预览


文档简介
2021-2022学年湖南省郴州市九年级(上)联考数学试卷(12月份)
一、单选题(共24分)
1.(3分)把抛物线向右平移1个单位,所得抛物线的函数表达式为
A. B. C. D.
2.(3分)上海世博会的某纪念品原价168元,连续两次降价后售价为128元.下列所列方程中正确的是
A. B.
C. D.
3.(3分)从甲、乙、丙、丁四人中选一人参加射击比赛,经过三轮初赛,他们平均成绩都是9环,方差分别是,,,,从成绩稳定上看,你认为谁去最合适
A.甲 B.乙 C.丙 D.丁
4.(3分)若直线与反比例函数的图象交于点,则反比例函数的图象还必过点
A. B. C. D.
5.(3分)《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈尺,1尺寸),则竹竿的长为
A.五丈 B.四丈五尺 C.一丈 D.五尺
6.(3分)在直角三角形中,,,则的值是
A. B. C. D.
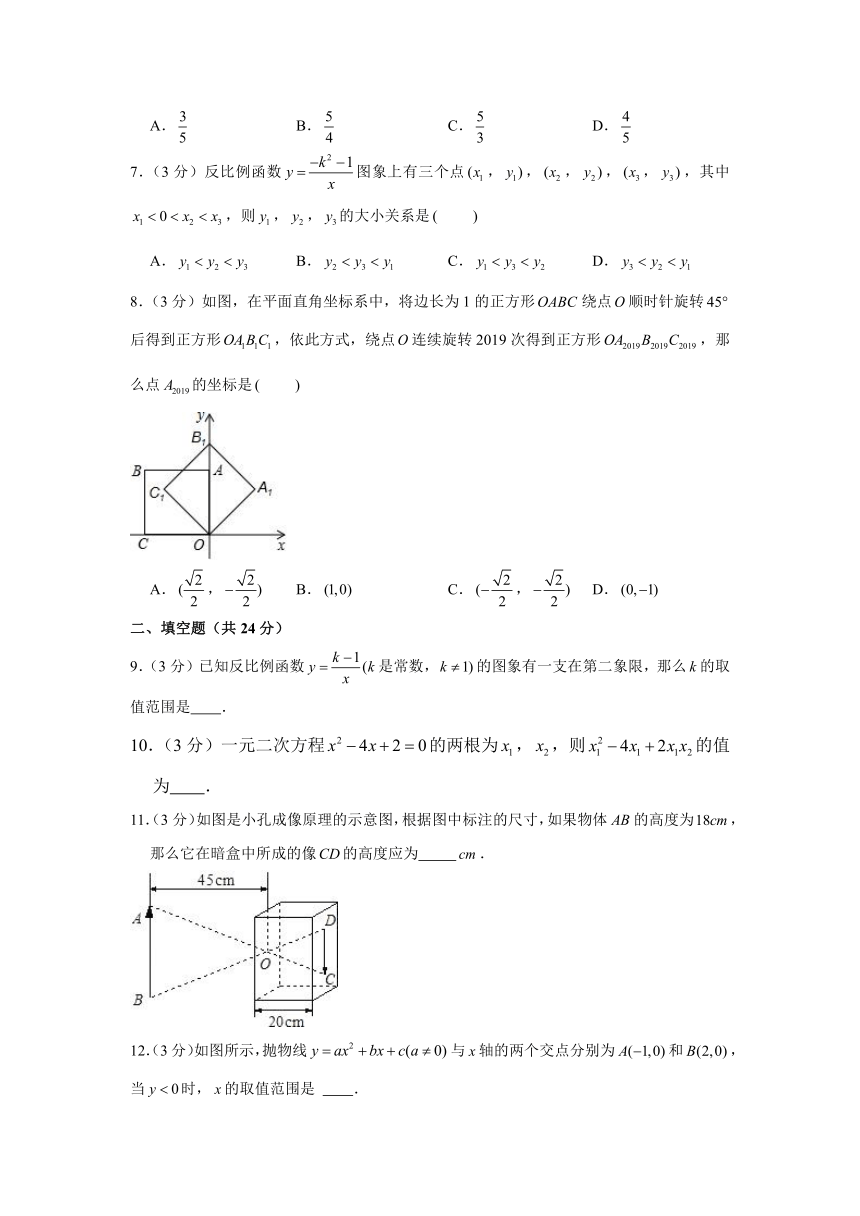
7.(3分)反比例函数图象上有三个点,,,,,,其中,则,,的大小关系是
A. B. C. D.
8.(3分)如图,在平面直角坐标系中,将边长为1的正方形绕点顺时针旋转后得到正方形,依此方式,绕点连续旋转2019次得到正方形,那么点的坐标是
A., B. C., D.
二、填空题(共24分)
9.(3分)已知反比例函数是常数,的图象有一支在第二象限,那么的取值范围是 .
10.(3分)一元二次方程的两根为,,则的值为 .
11.(3分)如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体的高度为,那么它在暗盒中所成的像的高度应为 .
12.(3分)如图所示,抛物线与轴的两个交点分别为和,当时,的取值范围是 .
13.(3分)如图,在反比例函数图象上,轴于,则的值为 .
14.(3分)三角形两边的长是3和4,第三边的长是方程的根,则该三角形的周长为 .
15.(3分)在中,若、满足,则 .
16.(3分)如图,矩形的顶点,在轴上,且关于轴对称,反比例函数的图象经过点,反比例函数的图象分别与,交于点,,若,,则等于 .
三、解答题(共82分)
17.(6分)计算:.
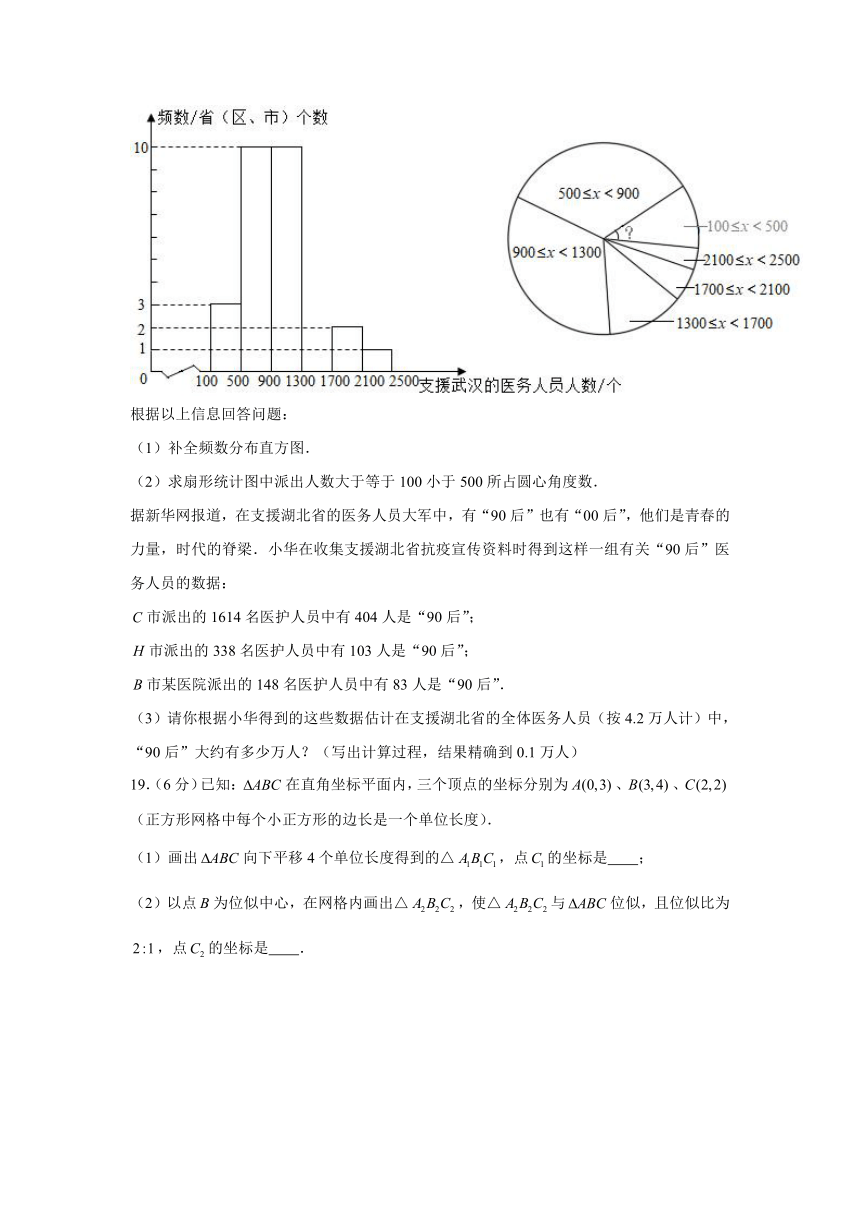
18.(6分)病毒虽无情,人间有大爱.2020年,在湖北省抗击新冠病毒的战“疫”中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省.全国30个省(区、市)各派出支援武汉的医务人员频数分布直方图(不完整)和扇形统计图如下:(数据分成6组:,,,,,.
根据以上信息回答问题:
(1)补全频数分布直方图.
(2)求扇形统计图中派出人数大于等于100小于500所占圆心角度数.
据新华网报道,在支援湖北省的医务人员大军中,有“90后”也有“00后”,他们是青春的力量,时代的脊梁.小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据:
市派出的1614名医护人员中有404人是“90后”;
市派出的338名医护人员中有103人是“90后”;
市某医院派出的148名医护人员中有83人是“90后”.
(3)请你根据小华得到的这些数据估计在支援湖北省的全体医务人员(按4.2万人计)中,“90后”大约有多少万人?(写出计算过程,结果精确到0.1万人)
19.(6分)已知:在直角坐标平面内,三个顶点的坐标分别为、、(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出向下平移4个单位长度得到的△,点的坐标是 ;
(2)以点为位似中心,在网格内画出△,使△与位似,且位似比为,点的坐标是 .
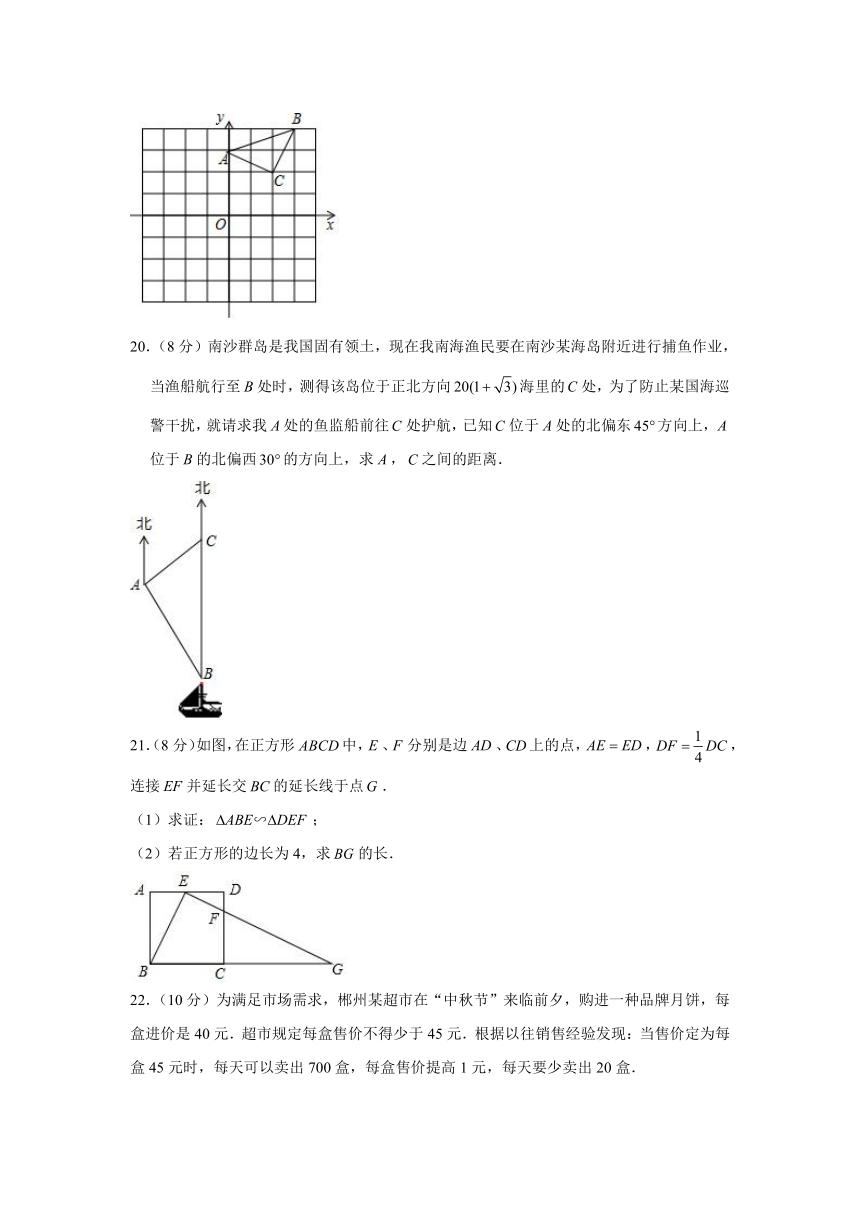
20.(8分)南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至处时,测得该岛位于正北方向海里的处,为了防止某国海巡警干扰,就请求我处的鱼监船前往处护航,已知位于处的北偏东方向上,位于的北偏西的方向上,求,之间的距离.
21.(8分)如图,在正方形中,、分别是边、上的点,,,连接并延长交的延长线于点.
(1)求证:;
(2)若正方形的边长为4,求的长.
22.(10分)为满足市场需求,郴州某超市在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价提高1元,每天要少卖出20盒.
(1)试求出每天的销售量(盒与每盒售价(元之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润(元最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种月饼的每盒售价不得高于57元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售月饼多少盒?
23.(8分)阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程,可以通过因式分解把它转化为,解方程和,可得方程的解.
(1)问题:方程的解是, , ;
(2)拓展:用“转化”思想求方程的解.
24.(8分)如图,在平面直角坐标系中,矩形的顶点在轴上,在轴上,反比例函数的图象分别交,于,,已知,.
(1)求的值;
(2)若,求点的坐标.
25.(10分)如图,在中,,,点从点出发,沿着以每秒的速度向点运动,同时点从点出发,沿着以每秒的速度向点运动,设运动时间为秒.
(1)为何值时,四边形是梯形?
(2)是否存在某一时刻,使与相似?若存在,求出此时的长;若不存在,请说明理由;
(3)当时,求的值.
26.(12分)如图,已知抛物线经过,及原点,顶点为
(1)求抛物线的函数解析式.
(2)设点在抛物线上,点在抛物线的对称轴上,且以为边的四边形是平行四边形,求点的坐标.
(3)是抛物线上第一象限内的动点,过点作轴,垂足为,是否存在点,使得以、、为顶点的三角形与相似?若存在,求出点的坐标;若不存在,请说明理由.
参考答案与解析
一、单选题(共24分)
1.(3分)把抛物线向右平移1个单位,所得抛物线的函数表达式为
A. B. C. D.
【解答】解:原抛物线的顶点为,向右平移1个单位,那么新抛物线的顶点为;
可设新抛物线的解析式为代入得:,
故选:.
2.(3分)上海世博会的某纪念品原价168元,连续两次降价后售价为128元.下列所列方程中正确的是
A. B.
C. D.
【解答】解:当商品第一次降价时,其售价为;
当商品第二次降价后,其售价为.
.故选:.
3.(3分)从甲、乙、丙、丁四人中选一人参加射击比赛,经过三轮初赛,他们平均成绩都是9环,方差分别是,,,,从成绩稳定上看,你认为谁去最合适
A.甲 B.乙 C.丙 D.丁
【解答】解:,
,
甲的成绩稳定,
选甲最合适,
故选:.
4.(3分)若直线与反比例函数的图象交于点,则反比例函数的图象还必过点
A. B. C. D.
【解答】解:直线经过点,
,把这点代入解析式,解得,
则反比例函数的解析式是,四个选项中只有.
故选:.
5.(3分)《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈尺,1尺寸),则竹竿的长为
A.五丈 B.四丈五尺 C.一丈 D.五尺
【解答】解:设竹竿的长度为尺,
竹竿的影长一丈五尺尺,标杆长一尺五寸尺,影长五寸尺,
,解得(尺.
故选:.
6.(3分)在直角三角形中,,,则的值是
A. B. C. D.
【解答】解:在直角三角形中,,
由于,可设,则,
由勾股定理得,,
,
故选:.
7.(3分)反比例函数图象上有三个点,,,,,,其中,则,,的大小关系是
A. B. C. D.
【解答】解:反比例函数中,,
此函数的图象在二、四象限,在每一象限内随的增大而增大,
,
、,
.
故选:.
8.(3分)如图,在平面直角坐标系中,将边长为1的正方形绕点顺时针旋转后得到正方形,依此方式,绕点连续旋转2019次得到正方形,那么点的坐标是
A., B. C., D.
【解答】解:四边形是正方形,且,
,
将正方形绕点顺时针旋转后得到正方形,
,,,,,,
发现是8次一循环,所以余3,
点的坐标为,
故选:.
二、填空题(共24分)
9.(3分)已知反比例函数是常数,的图象有一支在第二象限,那么的取值范围是 .
【解答】解:反比例函数的图象有一支在第二象限,
,
解得.
故答案为:.
10.(3分)一元二次方程的两根为,,则的值为 2 .
【解答】解:一元二次方程的两根为、,
,,
.
故答案为: 2 .
11.(3分)如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体的高度为,那么它在暗盒中所成的像的高度应为 8 .
【解答】解:
,
又,
.
故答案为:8.
12.(3分)如图所示,抛物线与轴的两个交点分别为和,当时,的取值范围是 或 .
【解答】解:观察图象可知,抛物线与轴两交点为,,
,图象在轴的下方,所以答案是或.
13.(3分)如图,在反比例函数图象上,轴于,则的值为 .
【解答】解:在反比例函数图象上,
,
轴于,
,,
,
故答案为:.
14.(3分)三角形两边的长是3和4,第三边的长是方程的根,则该三角形的周长为 12 .
【解答】解:解方程,
得,,
第三边,
第三边长为5,
周长为.
15.(3分)在中,若、满足,则 .
【解答】解:,
,,
,,
,,
则,
故答案为:.
16.(3分)如图,矩形的顶点,在轴上,且关于轴对称,反比例函数的图象经过点,反比例函数的图象分别与,交于点,,若,,则等于 9 .
【解答】解:设点的坐标为,则点坐标为
由图象可知,点,,,,
矩形面积为:
①
代入①式得
解得
故答案为:9
三、解答题(共82分)
17.(6分)计算:.
【解答】解:原式
.
18.(6分)病毒虽无情,人间有大爱.2020年,在湖北省抗击新冠病毒的战“疫”中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省.全国30个省(区、市)各派出支援武汉的医务人员频数分布直方图(不完整)和扇形统计图如下:(数据分成6组:,,,,,.
根据以上信息回答问题:
(1)补全频数分布直方图.
(2)求扇形统计图中派出人数大于等于100小于500所占圆心角度数.
据新华网报道,在支援湖北省的医务人员大军中,有“90后”也有“00后”,他们是青春的力量,时代的脊梁.小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据:
市派出的1614名医护人员中有404人是“90后”;
市派出的338名医护人员中有103人是“90后”;
市某医院派出的148名医护人员中有83人是“90后”.
(3)请你根据小华得到的这些数据估计在支援湖北省的全体医务人员(按4.2万人计)中,“90后”大约有多少万人?(写出计算过程,结果精确到0.1万人)
【解答】解:(1)由直方图可得,
,这一组的频数是:,
补全的频数分布直方图如右图所示;
(2),
即扇形统计图中派出人数大于等于100小于500所占圆心角度数是;
(3)(万人),
答:在支援湖北省的全体医务人员(按4.2万人计)中,“90后”大约有1.2万人.
19.(6分)已知:在直角坐标平面内,三个顶点的坐标分别为、、(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出向下平移4个单位长度得到的△,点的坐标是 ;
(2)以点为位似中心,在网格内画出△,使△与位似,且位似比为,点的坐标是 .
【解答】解:(1)如图所示,画出向下平移4个单位长度得到的△,点的坐标是;
(2)如图所示,以为位似中心,画出△,使△与位似,且位似比为,点的坐标是,
故答案为:(1);(2)
20.(8分)南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至处时,测得该岛位于正北方向海里的处,为了防止某国海巡警干扰,就请求我处的鱼监船前往处护航,已知位于处的北偏东方向上,位于的北偏西的方向上,求,之间的距离.
【解答】解:作于,
设海里,
在中,,
则,
在中,,
则
解得,,
答:,之间的距离为海里.
21.(8分)如图,在正方形中,、分别是边、上的点,,,连接并延长交的延长线于点.
(1)求证:;
(2)若正方形的边长为4,求的长.
【解答】(1)证明:四边形为正方形,
,,
,
,
,
,
,
;
(2)解:四边形为正方形,
,
,
又,正方形的边长为4,
,,
.
22.(10分)为满足市场需求,郴州某超市在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价提高1元,每天要少卖出20盒.
(1)试求出每天的销售量(盒与每盒售价(元之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润(元最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种月饼的每盒售价不得高于57元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售月饼多少盒?
【解答】解:(1)由题意得:;
(2),
,,
当时,元,
即当每盒售价定为60元时,每天销售的利润(元最大,最大利润是8000元;
(3)由题意,得,
解得,,
抛物线的开口向下,
当时,每天销售糕点的利润不低于6000元的利润,
又,
.
在中,,
随的增大而减小,
当时,,
即超市每天至少销售糕点440盒.
23.(8分)阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程,可以通过因式分解把它转化为,解方程和,可得方程的解.
(1)问题:方程的解是, , ;
(2)拓展:用“转化”思想求方程的解.
【解答】解:(1),
,
.
或或.
,,.
故答案为:,1.
(2)方程两边平方,得,
.
.
,.
经检验,是原方程的解.
所以原方程的解为:.
24.(8分)如图,在平面直角坐标系中,矩形的顶点在轴上,在轴上,反比例函数的图象分别交,于,,已知,.
(1)求的值;
(2)若,求点的坐标.
【解答】解:(1),,
的坐标为,
点在反比例函数的图象上,
,即的值为6;
(2)设、,
的坐标为,
,.
,
,
解得或(舍去).
,
.
25.(10分)如图,在中,,,点从点出发,沿着以每秒的速度向点运动,同时点从点出发,沿着以每秒的速度向点运动,设运动时间为秒.
(1)为何值时,四边形是梯形?
(2)是否存在某一时刻,使与相似?若存在,求出此时的长;若不存在,请说明理由;
(3)当时,求的值.
【解答】解:(1)由题意知,
四边形是梯形,
,
,
,,
,
,
,
当时,四边形是梯形;
(2)存在,
则,
,
,
当的长为时,,
(3),
,
又,
,
即,
,
此时,,
.
.
26.(12分)如图,已知抛物线经过,及原点,顶点为
(1)求抛物线的函数解析式.
(2)设点在抛物线上,点在抛物线的对称轴上,且以为边的四边形是平行四边形,求点的坐标.
(3)是抛物线上第一象限内的动点,过点作轴,垂足为,是否存在点,使得以、、为顶点的三角形与相似?若存在,求出点的坐标;若不存在,请说明理由.
【解答】解:(1)设抛物线的解析式为,
将点,,,代入可得:,
解得:.
故函数解析式为:.
(2)当为平行四边形的边时,,,由知:,
由四边形可知在对称轴直线右侧,
则横坐标为1,代入抛物线解析式得.
综上可得点的坐标为:.
(3)存在.
如图:,,
根据勾股定理得:,,,
,
是直角三角形,
假设存在点,使以,,为顶点的 三角形与相似,
设,由题意知,,且,
①若,则,
即,
得:,(舍去).
当时,,即,,
②若,则,
即:,
得:,(舍去)
当时,,即.
故符合条件的点有两个,分别是,或.
一、单选题(共24分)
1.(3分)把抛物线向右平移1个单位,所得抛物线的函数表达式为
A. B. C. D.
2.(3分)上海世博会的某纪念品原价168元,连续两次降价后售价为128元.下列所列方程中正确的是
A. B.
C. D.
3.(3分)从甲、乙、丙、丁四人中选一人参加射击比赛,经过三轮初赛,他们平均成绩都是9环,方差分别是,,,,从成绩稳定上看,你认为谁去最合适
A.甲 B.乙 C.丙 D.丁
4.(3分)若直线与反比例函数的图象交于点,则反比例函数的图象还必过点
A. B. C. D.
5.(3分)《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈尺,1尺寸),则竹竿的长为
A.五丈 B.四丈五尺 C.一丈 D.五尺
6.(3分)在直角三角形中,,,则的值是
A. B. C. D.
7.(3分)反比例函数图象上有三个点,,,,,,其中,则,,的大小关系是
A. B. C. D.
8.(3分)如图,在平面直角坐标系中,将边长为1的正方形绕点顺时针旋转后得到正方形,依此方式,绕点连续旋转2019次得到正方形,那么点的坐标是
A., B. C., D.
二、填空题(共24分)
9.(3分)已知反比例函数是常数,的图象有一支在第二象限,那么的取值范围是 .
10.(3分)一元二次方程的两根为,,则的值为 .
11.(3分)如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体的高度为,那么它在暗盒中所成的像的高度应为 .
12.(3分)如图所示,抛物线与轴的两个交点分别为和,当时,的取值范围是 .
13.(3分)如图,在反比例函数图象上,轴于,则的值为 .
14.(3分)三角形两边的长是3和4,第三边的长是方程的根,则该三角形的周长为 .
15.(3分)在中,若、满足,则 .
16.(3分)如图,矩形的顶点,在轴上,且关于轴对称,反比例函数的图象经过点,反比例函数的图象分别与,交于点,,若,,则等于 .
三、解答题(共82分)
17.(6分)计算:.
18.(6分)病毒虽无情,人间有大爱.2020年,在湖北省抗击新冠病毒的战“疫”中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省.全国30个省(区、市)各派出支援武汉的医务人员频数分布直方图(不完整)和扇形统计图如下:(数据分成6组:,,,,,.
根据以上信息回答问题:
(1)补全频数分布直方图.
(2)求扇形统计图中派出人数大于等于100小于500所占圆心角度数.
据新华网报道,在支援湖北省的医务人员大军中,有“90后”也有“00后”,他们是青春的力量,时代的脊梁.小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据:
市派出的1614名医护人员中有404人是“90后”;
市派出的338名医护人员中有103人是“90后”;
市某医院派出的148名医护人员中有83人是“90后”.
(3)请你根据小华得到的这些数据估计在支援湖北省的全体医务人员(按4.2万人计)中,“90后”大约有多少万人?(写出计算过程,结果精确到0.1万人)
19.(6分)已知:在直角坐标平面内,三个顶点的坐标分别为、、(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出向下平移4个单位长度得到的△,点的坐标是 ;
(2)以点为位似中心,在网格内画出△,使△与位似,且位似比为,点的坐标是 .
20.(8分)南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至处时,测得该岛位于正北方向海里的处,为了防止某国海巡警干扰,就请求我处的鱼监船前往处护航,已知位于处的北偏东方向上,位于的北偏西的方向上,求,之间的距离.
21.(8分)如图,在正方形中,、分别是边、上的点,,,连接并延长交的延长线于点.
(1)求证:;
(2)若正方形的边长为4,求的长.
22.(10分)为满足市场需求,郴州某超市在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价提高1元,每天要少卖出20盒.
(1)试求出每天的销售量(盒与每盒售价(元之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润(元最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种月饼的每盒售价不得高于57元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售月饼多少盒?
23.(8分)阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程,可以通过因式分解把它转化为,解方程和,可得方程的解.
(1)问题:方程的解是, , ;
(2)拓展:用“转化”思想求方程的解.
24.(8分)如图,在平面直角坐标系中,矩形的顶点在轴上,在轴上,反比例函数的图象分别交,于,,已知,.
(1)求的值;
(2)若,求点的坐标.
25.(10分)如图,在中,,,点从点出发,沿着以每秒的速度向点运动,同时点从点出发,沿着以每秒的速度向点运动,设运动时间为秒.
(1)为何值时,四边形是梯形?
(2)是否存在某一时刻,使与相似?若存在,求出此时的长;若不存在,请说明理由;
(3)当时,求的值.
26.(12分)如图,已知抛物线经过,及原点,顶点为
(1)求抛物线的函数解析式.
(2)设点在抛物线上,点在抛物线的对称轴上,且以为边的四边形是平行四边形,求点的坐标.
(3)是抛物线上第一象限内的动点,过点作轴,垂足为,是否存在点,使得以、、为顶点的三角形与相似?若存在,求出点的坐标;若不存在,请说明理由.
参考答案与解析
一、单选题(共24分)
1.(3分)把抛物线向右平移1个单位,所得抛物线的函数表达式为
A. B. C. D.
【解答】解:原抛物线的顶点为,向右平移1个单位,那么新抛物线的顶点为;
可设新抛物线的解析式为代入得:,
故选:.
2.(3分)上海世博会的某纪念品原价168元,连续两次降价后售价为128元.下列所列方程中正确的是
A. B.
C. D.
【解答】解:当商品第一次降价时,其售价为;
当商品第二次降价后,其售价为.
.故选:.
3.(3分)从甲、乙、丙、丁四人中选一人参加射击比赛,经过三轮初赛,他们平均成绩都是9环,方差分别是,,,,从成绩稳定上看,你认为谁去最合适
A.甲 B.乙 C.丙 D.丁
【解答】解:,
,
甲的成绩稳定,
选甲最合适,
故选:.
4.(3分)若直线与反比例函数的图象交于点,则反比例函数的图象还必过点
A. B. C. D.
【解答】解:直线经过点,
,把这点代入解析式,解得,
则反比例函数的解析式是,四个选项中只有.
故选:.
5.(3分)《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈尺,1尺寸),则竹竿的长为
A.五丈 B.四丈五尺 C.一丈 D.五尺
【解答】解:设竹竿的长度为尺,
竹竿的影长一丈五尺尺,标杆长一尺五寸尺,影长五寸尺,
,解得(尺.
故选:.
6.(3分)在直角三角形中,,,则的值是
A. B. C. D.
【解答】解:在直角三角形中,,
由于,可设,则,
由勾股定理得,,
,
故选:.
7.(3分)反比例函数图象上有三个点,,,,,,其中,则,,的大小关系是
A. B. C. D.
【解答】解:反比例函数中,,
此函数的图象在二、四象限,在每一象限内随的增大而增大,
,
、,
.
故选:.
8.(3分)如图,在平面直角坐标系中,将边长为1的正方形绕点顺时针旋转后得到正方形,依此方式,绕点连续旋转2019次得到正方形,那么点的坐标是
A., B. C., D.
【解答】解:四边形是正方形,且,
,
将正方形绕点顺时针旋转后得到正方形,
,,,,,,
发现是8次一循环,所以余3,
点的坐标为,
故选:.
二、填空题(共24分)
9.(3分)已知反比例函数是常数,的图象有一支在第二象限,那么的取值范围是 .
【解答】解:反比例函数的图象有一支在第二象限,
,
解得.
故答案为:.
10.(3分)一元二次方程的两根为,,则的值为 2 .
【解答】解:一元二次方程的两根为、,
,,
.
故答案为: 2 .
11.(3分)如图是小孔成像原理的示意图,根据图中标注的尺寸,如果物体的高度为,那么它在暗盒中所成的像的高度应为 8 .
【解答】解:
,
又,
.
故答案为:8.
12.(3分)如图所示,抛物线与轴的两个交点分别为和,当时,的取值范围是 或 .
【解答】解:观察图象可知,抛物线与轴两交点为,,
,图象在轴的下方,所以答案是或.
13.(3分)如图,在反比例函数图象上,轴于,则的值为 .
【解答】解:在反比例函数图象上,
,
轴于,
,,
,
故答案为:.
14.(3分)三角形两边的长是3和4,第三边的长是方程的根,则该三角形的周长为 12 .
【解答】解:解方程,
得,,
第三边,
第三边长为5,
周长为.
15.(3分)在中,若、满足,则 .
【解答】解:,
,,
,,
,,
则,
故答案为:.
16.(3分)如图,矩形的顶点,在轴上,且关于轴对称,反比例函数的图象经过点,反比例函数的图象分别与,交于点,,若,,则等于 9 .
【解答】解:设点的坐标为,则点坐标为
由图象可知,点,,,,
矩形面积为:
①
代入①式得
解得
故答案为:9
三、解答题(共82分)
17.(6分)计算:.
【解答】解:原式
.
18.(6分)病毒虽无情,人间有大爱.2020年,在湖北省抗击新冠病毒的战“疫”中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省.全国30个省(区、市)各派出支援武汉的医务人员频数分布直方图(不完整)和扇形统计图如下:(数据分成6组:,,,,,.
根据以上信息回答问题:
(1)补全频数分布直方图.
(2)求扇形统计图中派出人数大于等于100小于500所占圆心角度数.
据新华网报道,在支援湖北省的医务人员大军中,有“90后”也有“00后”,他们是青春的力量,时代的脊梁.小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据:
市派出的1614名医护人员中有404人是“90后”;
市派出的338名医护人员中有103人是“90后”;
市某医院派出的148名医护人员中有83人是“90后”.
(3)请你根据小华得到的这些数据估计在支援湖北省的全体医务人员(按4.2万人计)中,“90后”大约有多少万人?(写出计算过程,结果精确到0.1万人)
【解答】解:(1)由直方图可得,
,这一组的频数是:,
补全的频数分布直方图如右图所示;
(2),
即扇形统计图中派出人数大于等于100小于500所占圆心角度数是;
(3)(万人),
答:在支援湖北省的全体医务人员(按4.2万人计)中,“90后”大约有1.2万人.
19.(6分)已知:在直角坐标平面内,三个顶点的坐标分别为、、(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出向下平移4个单位长度得到的△,点的坐标是 ;
(2)以点为位似中心,在网格内画出△,使△与位似,且位似比为,点的坐标是 .
【解答】解:(1)如图所示,画出向下平移4个单位长度得到的△,点的坐标是;
(2)如图所示,以为位似中心,画出△,使△与位似,且位似比为,点的坐标是,
故答案为:(1);(2)
20.(8分)南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至处时,测得该岛位于正北方向海里的处,为了防止某国海巡警干扰,就请求我处的鱼监船前往处护航,已知位于处的北偏东方向上,位于的北偏西的方向上,求,之间的距离.
【解答】解:作于,
设海里,
在中,,
则,
在中,,
则
解得,,
答:,之间的距离为海里.
21.(8分)如图,在正方形中,、分别是边、上的点,,,连接并延长交的延长线于点.
(1)求证:;
(2)若正方形的边长为4,求的长.
【解答】(1)证明:四边形为正方形,
,,
,
,
,
,
,
;
(2)解:四边形为正方形,
,
,
又,正方形的边长为4,
,,
.
22.(10分)为满足市场需求,郴州某超市在“中秋节”来临前夕,购进一种品牌月饼,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价提高1元,每天要少卖出20盒.
(1)试求出每天的销售量(盒与每盒售价(元之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润(元最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种月饼的每盒售价不得高于57元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售月饼多少盒?
【解答】解:(1)由题意得:;
(2),
,,
当时,元,
即当每盒售价定为60元时,每天销售的利润(元最大,最大利润是8000元;
(3)由题意,得,
解得,,
抛物线的开口向下,
当时,每天销售糕点的利润不低于6000元的利润,
又,
.
在中,,
随的增大而减小,
当时,,
即超市每天至少销售糕点440盒.
23.(8分)阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验各类方程的解法不尽相同,但是它们有一个共同的基本数学思想转化,把未知转化为已知用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程,可以通过因式分解把它转化为,解方程和,可得方程的解.
(1)问题:方程的解是, , ;
(2)拓展:用“转化”思想求方程的解.
【解答】解:(1),
,
.
或或.
,,.
故答案为:,1.
(2)方程两边平方,得,
.
.
,.
经检验,是原方程的解.
所以原方程的解为:.
24.(8分)如图,在平面直角坐标系中,矩形的顶点在轴上,在轴上,反比例函数的图象分别交,于,,已知,.
(1)求的值;
(2)若,求点的坐标.
【解答】解:(1),,
的坐标为,
点在反比例函数的图象上,
,即的值为6;
(2)设、,
的坐标为,
,.
,
,
解得或(舍去).
,
.
25.(10分)如图,在中,,,点从点出发,沿着以每秒的速度向点运动,同时点从点出发,沿着以每秒的速度向点运动,设运动时间为秒.
(1)为何值时,四边形是梯形?
(2)是否存在某一时刻,使与相似?若存在,求出此时的长;若不存在,请说明理由;
(3)当时,求的值.
【解答】解:(1)由题意知,
四边形是梯形,
,
,
,,
,
,
,
当时,四边形是梯形;
(2)存在,
则,
,
,
当的长为时,,
(3),
,
又,
,
即,
,
此时,,
.
.
26.(12分)如图,已知抛物线经过,及原点,顶点为
(1)求抛物线的函数解析式.
(2)设点在抛物线上,点在抛物线的对称轴上,且以为边的四边形是平行四边形,求点的坐标.
(3)是抛物线上第一象限内的动点,过点作轴,垂足为,是否存在点,使得以、、为顶点的三角形与相似?若存在,求出点的坐标;若不存在,请说明理由.
【解答】解:(1)设抛物线的解析式为,
将点,,,代入可得:,
解得:.
故函数解析式为:.
(2)当为平行四边形的边时,,,由知:,
由四边形可知在对称轴直线右侧,
则横坐标为1,代入抛物线解析式得.
综上可得点的坐标为:.
(3)存在.
如图:,,
根据勾股定理得:,,,
,
是直角三角形,
假设存在点,使以,,为顶点的 三角形与相似,
设,由题意知,,且,
①若,则,
即,
得:,(舍去).
当时,,即,,
②若,则,
即:,
得:,(舍去)
当时,,即.
故符合条件的点有两个,分别是,或.
同课章节目录
