2021-2022学年鲁教版(五四制)九年级数学下册5.4圆周角和圆心角的关系 期末综合复习训练2(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学下册5.4圆周角和圆心角的关系 期末综合复习训练2(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 346.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览



文档简介
2021-2022学年鲁教版九年级数学下册《5.4圆周角和圆心角的关系》
期末综合复习训练2(附答案)
1.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=( )
A.70° B.110° C.120° D.140°
2.如图,四边形ABCD内接于圆O,连接OB,OD,若∠BOD=∠BCD,则∠BAD的度数为( )
A.30° B.45° C.60° D.120°
3.如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为( )
A.57° B.52° C.38° D.26°
4.如图,⊙O的半径为1,AB是⊙O的一条弦,且AB=,则弦AB所对圆周角的度数为( )
A.30° B.60° C.30°或150° D.60°或120°
5.如图,点A、B、C、D在⊙O上,,∠CAD=30°,∠ACD=50°,则∠ADB=( )
A.30° B.50° C.70° D.80°
6.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP=( )
A.3 B.4 C.5 D.6
7.如图,半圆O的直径AB=7,两弦AC、BD相交于点E,弦CD=,且BD=5,则DE等于( )
A. B. C. D.
8.如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10° B.20° C.30° D.40°
9.如图,点C是以AB为直径的圆上一个动点(不与点A、B重合),且AC+BC=12.若AB=m(m为整数),则整数m的值的个数为( )
A.0个 B.2个 C.3个 D.4个
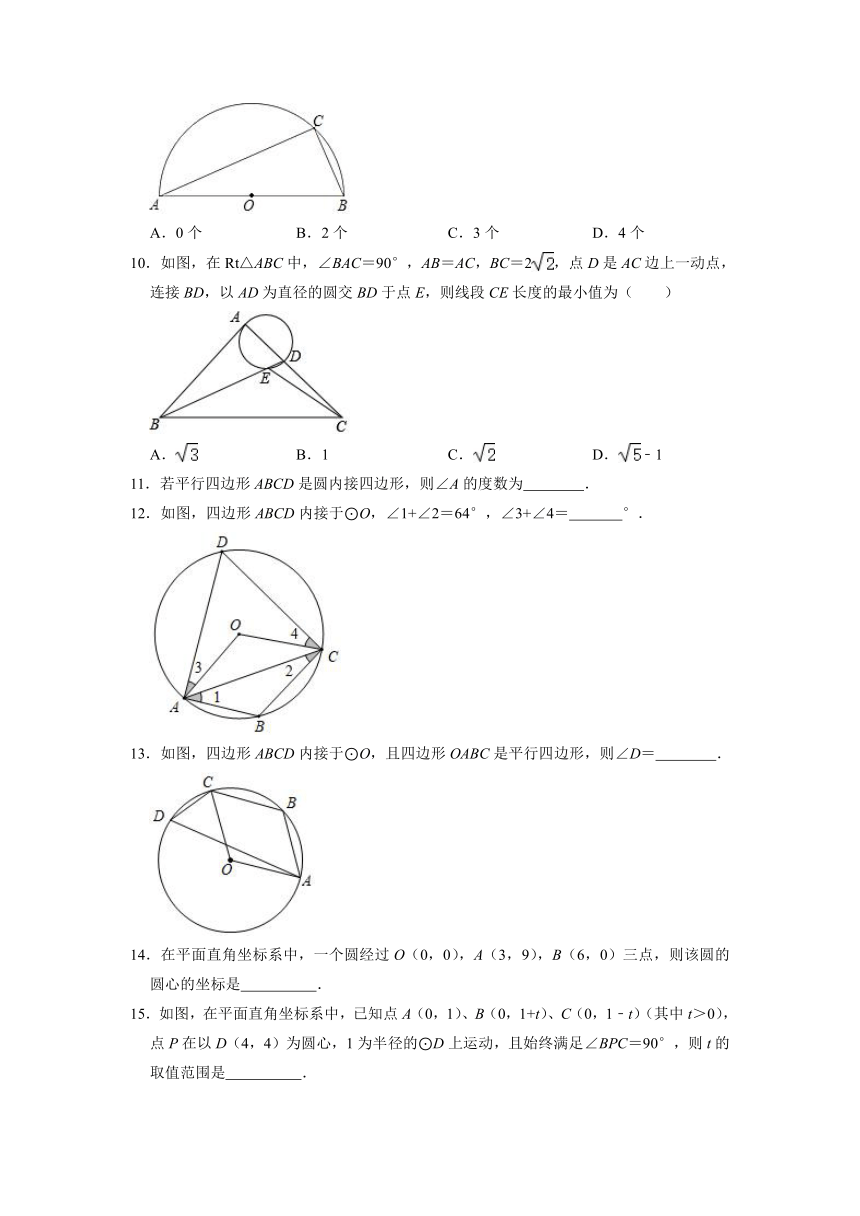
10.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
A. B.1 C. D.﹣1
11.若平行四边形ABCD是圆内接四边形,则∠A的度数为 .
12.如图,四边形ABCD内接于⊙O,∠1+∠2=64°,∠3+∠4= °.
13.如图,四边形ABCD内接于⊙O,且四边形OABC是平行四边形,则∠D= .
14.在平面直角坐标系中,一个圆经过O(0,0),A(3,9),B(6,0)三点,则该圆的圆心的坐标是 .
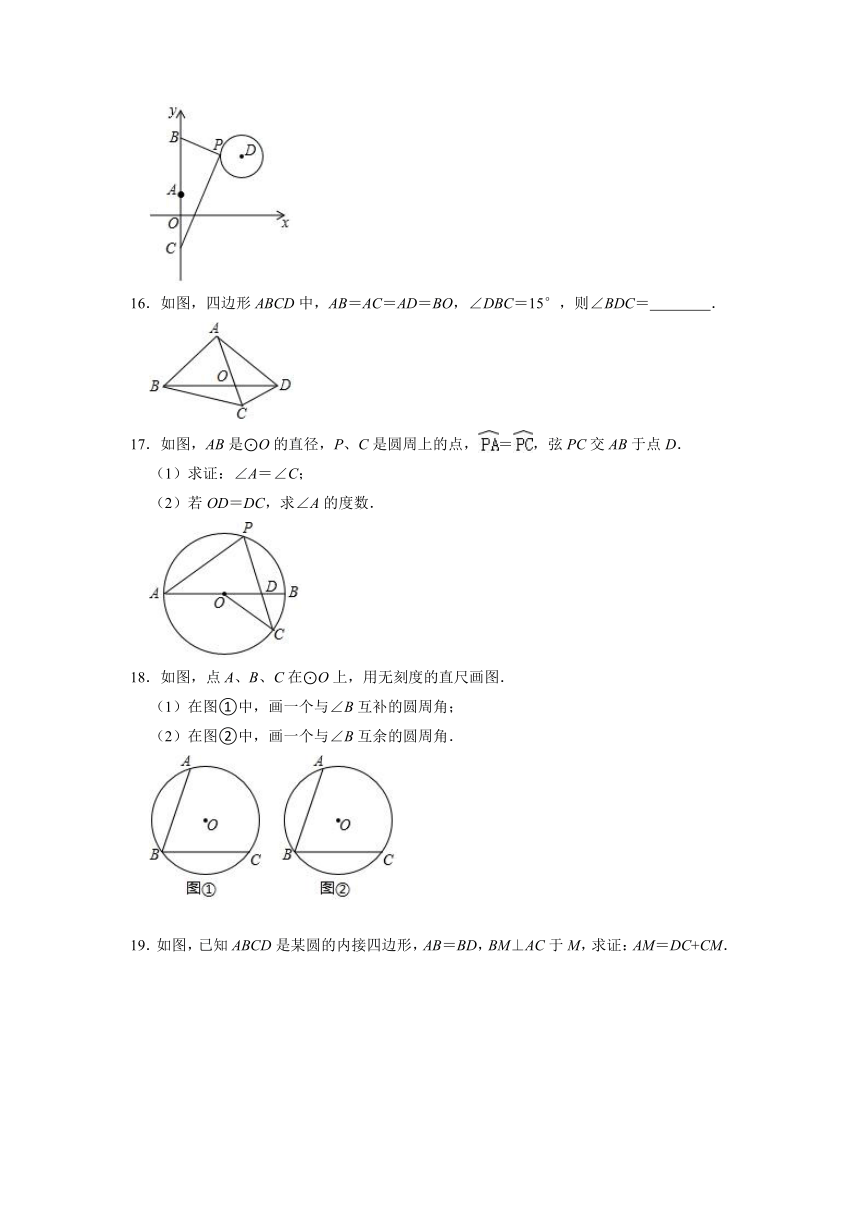
15.如图,在平面直角坐标系中,已知点A(0,1)、B(0,1+t)、C(0,1﹣t)(其中t>0),点P在以D(4,4)为圆心,1为半径的⊙D上运动,且始终满足∠BPC=90°,则t的取值范围是 .
16.如图,四边形ABCD中,AB=AC=AD=BO,∠DBC=15°,则∠BDC= .
17.如图,AB是⊙O的直径,P、C是圆周上的点,=,弦PC交AB于点D.
(1)求证:∠A=∠C;
(2)若OD=DC,求∠A的度数.
18.如图,点A、B、C在⊙O上,用无刻度的直尺画图.
(1)在图①中,画一个与∠B互补的圆周角;
(2)在图②中,画一个与∠B互余的圆周角.
19.如图,已知ABCD是某圆的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
20.如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连接AB、PB、AC,BP分别与AD、AC相交于点E、F.
(1)求证:AE=BE;
(2)判断BE与EF是否相等吗,并说明理由;
(3)小李通过操作发现CF=2AB,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出CF与AB正确的关系式.
参考答案
1.解:作所对的圆周角∠ADB,如图,
∵∠ACB+∠ADB=180°,
∴∠ADB=180°﹣110°=70°,
∴∠AOB=2∠ADB=140°.
故选:D.
2.解:设∠BAD=x,则∠BOD=2x,
∵∠BCD=∠BOD=2x,∠BAD+∠BCD=180°,
∴3x=180°,
∴x=60°,
∴∠BAD=60°,
故选:C.
3.解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=38°,
∴∠BAC=90°﹣∠ABC=52°,
∴∠BDC=∠BAC=52°.
故选:B.
4.解:如图,连接OA、OB,过O作AB的垂线;
在Rt△OAC中,OA=1,AC=;
∴∠AOC=60°,∠AOB=120°;
∴∠D=∠AOB=60°;
∵四边形ADBE是⊙O的内接四边形,
∴∠AEB=180°﹣∠D=120°;
因此弦AB所对的圆周角有两个:60°或120°;
故选:D.
5.解:∵,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ACB=∠ADB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°.
故选:C.
6.解:由相交弦定理得:PA PB=PC PD,
∴DP===6.
故选:D.
7.解法一:
∵∠D=∠A,∠DCA=∠ABD,
∴△AEB∽△DEC;
∴=;
设BE=2x,则DE=5﹣2x,EC=x,AE=2(5﹣2x);
连接BC,则∠ACB=90°;
Rt△BCE中,BE=2x,EC=x,则BC=x;
在Rt△ABC中,AC=AE+EC=10﹣3x,BC=x;
由勾股定理,得:AB2=AC2+BC2,
即:72=(10﹣3x)2+(x)2,
整理,得4x2﹣20x+17=0,解得x1=+,x2=﹣;
由于x<,故x=﹣;
则DE=5﹣2x=2.
解法二:连接OD,OC,AD,
∵OD=CD=OC
则∠DOC=60°,∠DAC=30°
又AB=7,BD=5,
∴AD=2,
在Rt△ADE中,∠DAC=30°,
所以DE=2.
故选:A.
8.解:连接BC,延长ED交⊙O于N,连接OD,并延长交⊙O于M,
∵∠AOC=80°,
∴的度数是80°,
∵点D为弦AC的中点,OA=OC,
∴∠AOD=∠COD,
∴=,
即M为的中点,
∴和的度数都是80°=40°,
∵>,
∴40°<的度数<80°,
∴20°<∠CED<40°,
∴选项C符合题意;选项A、选项B、选项D都不符合题意;
故选:C.
9.解:设AC=x,则BC=12﹣x,
∵点C是以AB为直径的半圆上一个动点(不与点A、B重合),
∴∠ACB=90°,
∴AB2=AC2+BC2,
∴m2=x2+(12﹣x)2,
∴m2=2[(x﹣6)2+36]
∵点C是以AB为直径的半圆上一个动点(不与点A、B重合),
∴0<x<12,
∴0≤(x﹣6)2<36,
∴72≤2[(x﹣6)2+36]<144,
又∵m为整数,
∴当2[(x﹣6)2+36]=81或2[(x﹣4)2+16]=100或2[(x﹣4)2+16]=121时,m为整数9或10或11,
则整数m的值的个数为3个,
故选:C.
10.解:连接AE,
∵以AD为直径的圆交BD于点E,
∴∠AED=90°,
∴点E在以AB为直径的圆O上,
连接OE,OC,
则CE≥OC﹣OE,
∵∠BAC=90°,AB=AC,
∴AC=AB=BC=2,
由勾股定理得,OC==,
∴线段CE长度的最小值为﹣1,
故选:D.
11.解:∵四边形ABCD为平行四边形,
∴∠A=∠C,
∵四边形ABCD是圆内接四边形,
∴∠A+∠C=180°,
∴2∠A=180°,
∴∠A=90°,
故答案为90°.
12.解:如图,
∵四边形ABCD内接于⊙O,
∴∠DAB+∠DCB=180°,∠B+∠D=180°,
又∵△AOC为等腰三角形,
∴∠5=∠OCA,
∴∠1+∠2+∠3+∠4+2∠5=180°,
∵∠1+∠2=64°,
∴∠3+∠4=180°﹣64°﹣2∠5=116°﹣2∠5,
∵∠1+∠2+∠B=180°,∠B+∠D=180°,
∴∠D=∠1+∠2=64°,
∴∠O=2∠D=128,
在等腰三角形AOC中,
2∠5=180°﹣∠O=180°﹣128°=52°,
∴∠3+∠4=116°﹣52°=64°,
故答案为64.
13.解:∵四边形OABC是平行四边形,
∴∠AOC=∠ABC,
∵∠D+∠ABC=180°,∠D=∠AOC=∠ABC,
∴设∠D=x,则∠ABC=2x,
∴x+2x=180°,
解得:x=60°,
故∠D=60°.
故答案为:60°.
14.解:由题意圆心在线段OB的垂直平分线上,
设圆心O′(3,m),则有32+m2=(9﹣m)2,
解得m=4,
∴圆心O′(3,4),
故答案为:(3,4).
15.解:连接AP,作射线AD.
由题意得,AB=(1+t)﹣1=t,AC=1﹣(1﹣t)=t,
∴AB=AC,
∵∠BPC=90°,
∴,
t要最大,就是点A到⊙D上的一点的距离最大,
∴P在AD延长线上,
∵A(0,1),D(4,4),
∴,
∴t的最大值是AP=AD+PD=5+1=6,
∴t的最小值是AP=AD﹣PD=5﹣1=4,
故t的取值范围为:4≤t≤6.
故答案为:4≤t≤6.
16.解:∵AB=AC=AD=BO,
∴点B、C、D在以A点为圆心,AB为半径的圆上,
∴∠BAC=2∠BDC,∠CAD=2∠DBC=2×15°=30°,
设∠BDC=x,则∠BAC=2x,
∵BO=BA,
∴∠BOA=2x,
∵∠BOA=∠OAD+∠ADO,
∴∠ADO=2x﹣30°,
∵AC=AD,
∴∠ADC=∠ACD=(180°﹣30°)=75°,
即2x﹣30°+x=75°,解得x=35°,
即∠BDC=35°.
故答案为35°.
17.(1)证明:如图,连接OP.
∵=,
∴PA=PC.
在△POA与△POC中,
.
∴△POA≌△POC(SSS).
∴∠A=∠C;
(2)解:设∠A=∠C=x°,则∠POB=2∠A=2x°.
∵OD=DC,
∴∠DOC=∠C=x°.
∴∠POC=3x°,
∵OP=OC,
∴∠OPC=∠C=x°,
在△POC中,x+3x+x=180°
x=36.
∴∠A=36°.
18.解:(1)如图1,∠P即为所求:
(2)如图2,∠CBQ即为所求.
19.证明:在MA上截取ME=MC,连接BE,
∵BM⊥AC,
∴BE=BC,
∴∠BEC=∠BCE,
∵AB=BD,
∴=,
∴∠ADB=∠BAD,
而∠ADB=∠BCE,
∴∠BCE=∠BAD,
又∵∠BCD+∠BAD=180°,∠BEA+∠BCE=180°,
∴∠BEA=∠BCD,
∵∠BAE=∠BDC,
∴△ABE≌△DBC,
∴AE=CD,
∴AM=AE+EM=DC+CM.
20.解:(1)如图1,连接AP,
∵BC是半⊙O的直径,
∴∠BAC=90°,
∵AD⊥BC于D,
∴∠ADB=90°,
∴∠ACB+∠ABC=∠BAD+∠ABD=90°,
∴∠ACB=∠BAD,
∵点A是弧BP的中点,
∴∠P=∠ACB=∠ABP,
∴∠ABE=∠BAE,
∴AE=BE;
(2)BE=EF,
理由是:∵BC是直径,AD⊥BC,
∴∠BAC=∠ADC=90°,
∴∠BAD=∠ACB,
∵A为弧BP中点,
∴∠ABP=∠ACB,
∴∠BAD=∠ABP,
∴BE=AE,∠FAD=∠AFB,
∴EF=AE,
∴BE=EF;
(3)小李的发现是正确的,
理由是:如图2,延长BA、CP,两线交于G,
∵P为半圆弧的中点,A是弧BP的中点,
∴∠PCF=∠GBP,∠CPF=∠BPG=90°,BP=PC,
在△PCF和△PBG中,
,
∴△PCF≌△PBG(ASA),
∴CF=BG,
∵BC为直径,
∴∠BAC=90°,
∵A为弧BP中点,
∴∠GCA=∠BCA,
在△BAC和△GAC中,
,
∴△BAC≌△GAC(ASA),
∴AG=AB=BG,
∴CF=2AB.
期末综合复习训练2(附答案)
1.如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=( )
A.70° B.110° C.120° D.140°
2.如图,四边形ABCD内接于圆O,连接OB,OD,若∠BOD=∠BCD,则∠BAD的度数为( )
A.30° B.45° C.60° D.120°
3.如图,AB为⊙O的直径,C,D是圆周上的两点,若∠ABC=38°,则锐角∠BDC的度数为( )
A.57° B.52° C.38° D.26°
4.如图,⊙O的半径为1,AB是⊙O的一条弦,且AB=,则弦AB所对圆周角的度数为( )
A.30° B.60° C.30°或150° D.60°或120°
5.如图,点A、B、C、D在⊙O上,,∠CAD=30°,∠ACD=50°,则∠ADB=( )
A.30° B.50° C.70° D.80°
6.如图,⊙O中弦AB,CD相交于点P,已知AP=3,BP=2,CP=1,则DP=( )
A.3 B.4 C.5 D.6
7.如图,半圆O的直径AB=7,两弦AC、BD相交于点E,弦CD=,且BD=5,则DE等于( )
A. B. C. D.
8.如图,在⊙O中,AB为直径,∠AOC=80°.点D为弦AC的中点,点E为上任意一点.则∠CED的大小可能是( )
A.10° B.20° C.30° D.40°
9.如图,点C是以AB为直径的圆上一个动点(不与点A、B重合),且AC+BC=12.若AB=m(m为整数),则整数m的值的个数为( )
A.0个 B.2个 C.3个 D.4个
10.如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
A. B.1 C. D.﹣1
11.若平行四边形ABCD是圆内接四边形,则∠A的度数为 .
12.如图,四边形ABCD内接于⊙O,∠1+∠2=64°,∠3+∠4= °.
13.如图,四边形ABCD内接于⊙O,且四边形OABC是平行四边形,则∠D= .
14.在平面直角坐标系中,一个圆经过O(0,0),A(3,9),B(6,0)三点,则该圆的圆心的坐标是 .
15.如图,在平面直角坐标系中,已知点A(0,1)、B(0,1+t)、C(0,1﹣t)(其中t>0),点P在以D(4,4)为圆心,1为半径的⊙D上运动,且始终满足∠BPC=90°,则t的取值范围是 .
16.如图,四边形ABCD中,AB=AC=AD=BO,∠DBC=15°,则∠BDC= .
17.如图,AB是⊙O的直径,P、C是圆周上的点,=,弦PC交AB于点D.
(1)求证:∠A=∠C;
(2)若OD=DC,求∠A的度数.
18.如图,点A、B、C在⊙O上,用无刻度的直尺画图.
(1)在图①中,画一个与∠B互补的圆周角;
(2)在图②中,画一个与∠B互余的圆周角.
19.如图,已知ABCD是某圆的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
20.如图,BC是半⊙O的直径,点P是半圆弧的中点,点A是弧BP的中点,AD⊥BC于D,连接AB、PB、AC,BP分别与AD、AC相交于点E、F.
(1)求证:AE=BE;
(2)判断BE与EF是否相等吗,并说明理由;
(3)小李通过操作发现CF=2AB,请问小李的发现是否正确?若正确,请说明理由;若不正确,请写出CF与AB正确的关系式.
参考答案
1.解:作所对的圆周角∠ADB,如图,
∵∠ACB+∠ADB=180°,
∴∠ADB=180°﹣110°=70°,
∴∠AOB=2∠ADB=140°.
故选:D.
2.解:设∠BAD=x,则∠BOD=2x,
∵∠BCD=∠BOD=2x,∠BAD+∠BCD=180°,
∴3x=180°,
∴x=60°,
∴∠BAD=60°,
故选:C.
3.解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=38°,
∴∠BAC=90°﹣∠ABC=52°,
∴∠BDC=∠BAC=52°.
故选:B.
4.解:如图,连接OA、OB,过O作AB的垂线;
在Rt△OAC中,OA=1,AC=;
∴∠AOC=60°,∠AOB=120°;
∴∠D=∠AOB=60°;
∵四边形ADBE是⊙O的内接四边形,
∴∠AEB=180°﹣∠D=120°;
因此弦AB所对的圆周角有两个:60°或120°;
故选:D.
5.解:∵,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ACB=∠ADB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°.
故选:C.
6.解:由相交弦定理得:PA PB=PC PD,
∴DP===6.
故选:D.
7.解法一:
∵∠D=∠A,∠DCA=∠ABD,
∴△AEB∽△DEC;
∴=;
设BE=2x,则DE=5﹣2x,EC=x,AE=2(5﹣2x);
连接BC,则∠ACB=90°;
Rt△BCE中,BE=2x,EC=x,则BC=x;
在Rt△ABC中,AC=AE+EC=10﹣3x,BC=x;
由勾股定理,得:AB2=AC2+BC2,
即:72=(10﹣3x)2+(x)2,
整理,得4x2﹣20x+17=0,解得x1=+,x2=﹣;
由于x<,故x=﹣;
则DE=5﹣2x=2.
解法二:连接OD,OC,AD,
∵OD=CD=OC
则∠DOC=60°,∠DAC=30°
又AB=7,BD=5,
∴AD=2,
在Rt△ADE中,∠DAC=30°,
所以DE=2.
故选:A.
8.解:连接BC,延长ED交⊙O于N,连接OD,并延长交⊙O于M,
∵∠AOC=80°,
∴的度数是80°,
∵点D为弦AC的中点,OA=OC,
∴∠AOD=∠COD,
∴=,
即M为的中点,
∴和的度数都是80°=40°,
∵>,
∴40°<的度数<80°,
∴20°<∠CED<40°,
∴选项C符合题意;选项A、选项B、选项D都不符合题意;
故选:C.
9.解:设AC=x,则BC=12﹣x,
∵点C是以AB为直径的半圆上一个动点(不与点A、B重合),
∴∠ACB=90°,
∴AB2=AC2+BC2,
∴m2=x2+(12﹣x)2,
∴m2=2[(x﹣6)2+36]
∵点C是以AB为直径的半圆上一个动点(不与点A、B重合),
∴0<x<12,
∴0≤(x﹣6)2<36,
∴72≤2[(x﹣6)2+36]<144,
又∵m为整数,
∴当2[(x﹣6)2+36]=81或2[(x﹣4)2+16]=100或2[(x﹣4)2+16]=121时,m为整数9或10或11,
则整数m的值的个数为3个,
故选:C.
10.解:连接AE,
∵以AD为直径的圆交BD于点E,
∴∠AED=90°,
∴点E在以AB为直径的圆O上,
连接OE,OC,
则CE≥OC﹣OE,
∵∠BAC=90°,AB=AC,
∴AC=AB=BC=2,
由勾股定理得,OC==,
∴线段CE长度的最小值为﹣1,
故选:D.
11.解:∵四边形ABCD为平行四边形,
∴∠A=∠C,
∵四边形ABCD是圆内接四边形,
∴∠A+∠C=180°,
∴2∠A=180°,
∴∠A=90°,
故答案为90°.
12.解:如图,
∵四边形ABCD内接于⊙O,
∴∠DAB+∠DCB=180°,∠B+∠D=180°,
又∵△AOC为等腰三角形,
∴∠5=∠OCA,
∴∠1+∠2+∠3+∠4+2∠5=180°,
∵∠1+∠2=64°,
∴∠3+∠4=180°﹣64°﹣2∠5=116°﹣2∠5,
∵∠1+∠2+∠B=180°,∠B+∠D=180°,
∴∠D=∠1+∠2=64°,
∴∠O=2∠D=128,
在等腰三角形AOC中,
2∠5=180°﹣∠O=180°﹣128°=52°,
∴∠3+∠4=116°﹣52°=64°,
故答案为64.
13.解:∵四边形OABC是平行四边形,
∴∠AOC=∠ABC,
∵∠D+∠ABC=180°,∠D=∠AOC=∠ABC,
∴设∠D=x,则∠ABC=2x,
∴x+2x=180°,
解得:x=60°,
故∠D=60°.
故答案为:60°.
14.解:由题意圆心在线段OB的垂直平分线上,
设圆心O′(3,m),则有32+m2=(9﹣m)2,
解得m=4,
∴圆心O′(3,4),
故答案为:(3,4).
15.解:连接AP,作射线AD.
由题意得,AB=(1+t)﹣1=t,AC=1﹣(1﹣t)=t,
∴AB=AC,
∵∠BPC=90°,
∴,
t要最大,就是点A到⊙D上的一点的距离最大,
∴P在AD延长线上,
∵A(0,1),D(4,4),
∴,
∴t的最大值是AP=AD+PD=5+1=6,
∴t的最小值是AP=AD﹣PD=5﹣1=4,
故t的取值范围为:4≤t≤6.
故答案为:4≤t≤6.
16.解:∵AB=AC=AD=BO,
∴点B、C、D在以A点为圆心,AB为半径的圆上,
∴∠BAC=2∠BDC,∠CAD=2∠DBC=2×15°=30°,
设∠BDC=x,则∠BAC=2x,
∵BO=BA,
∴∠BOA=2x,
∵∠BOA=∠OAD+∠ADO,
∴∠ADO=2x﹣30°,
∵AC=AD,
∴∠ADC=∠ACD=(180°﹣30°)=75°,
即2x﹣30°+x=75°,解得x=35°,
即∠BDC=35°.
故答案为35°.
17.(1)证明:如图,连接OP.
∵=,
∴PA=PC.
在△POA与△POC中,
.
∴△POA≌△POC(SSS).
∴∠A=∠C;
(2)解:设∠A=∠C=x°,则∠POB=2∠A=2x°.
∵OD=DC,
∴∠DOC=∠C=x°.
∴∠POC=3x°,
∵OP=OC,
∴∠OPC=∠C=x°,
在△POC中,x+3x+x=180°
x=36.
∴∠A=36°.
18.解:(1)如图1,∠P即为所求:
(2)如图2,∠CBQ即为所求.
19.证明:在MA上截取ME=MC,连接BE,
∵BM⊥AC,
∴BE=BC,
∴∠BEC=∠BCE,
∵AB=BD,
∴=,
∴∠ADB=∠BAD,
而∠ADB=∠BCE,
∴∠BCE=∠BAD,
又∵∠BCD+∠BAD=180°,∠BEA+∠BCE=180°,
∴∠BEA=∠BCD,
∵∠BAE=∠BDC,
∴△ABE≌△DBC,
∴AE=CD,
∴AM=AE+EM=DC+CM.
20.解:(1)如图1,连接AP,
∵BC是半⊙O的直径,
∴∠BAC=90°,
∵AD⊥BC于D,
∴∠ADB=90°,
∴∠ACB+∠ABC=∠BAD+∠ABD=90°,
∴∠ACB=∠BAD,
∵点A是弧BP的中点,
∴∠P=∠ACB=∠ABP,
∴∠ABE=∠BAE,
∴AE=BE;
(2)BE=EF,
理由是:∵BC是直径,AD⊥BC,
∴∠BAC=∠ADC=90°,
∴∠BAD=∠ACB,
∵A为弧BP中点,
∴∠ABP=∠ACB,
∴∠BAD=∠ABP,
∴BE=AE,∠FAD=∠AFB,
∴EF=AE,
∴BE=EF;
(3)小李的发现是正确的,
理由是:如图2,延长BA、CP,两线交于G,
∵P为半圆弧的中点,A是弧BP的中点,
∴∠PCF=∠GBP,∠CPF=∠BPG=90°,BP=PC,
在△PCF和△PBG中,
,
∴△PCF≌△PBG(ASA),
∴CF=BG,
∵BC为直径,
∴∠BAC=90°,
∵A为弧BP中点,
∴∠GCA=∠BCA,
在△BAC和△GAC中,
,
∴△BAC≌△GAC(ASA),
∴AG=AB=BG,
∴CF=2AB.
