2021-2022学年山东省菏泽市郓城县七年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年山东省菏泽市郓城县七年级(上)期中数学试卷(Word版 含解析) | 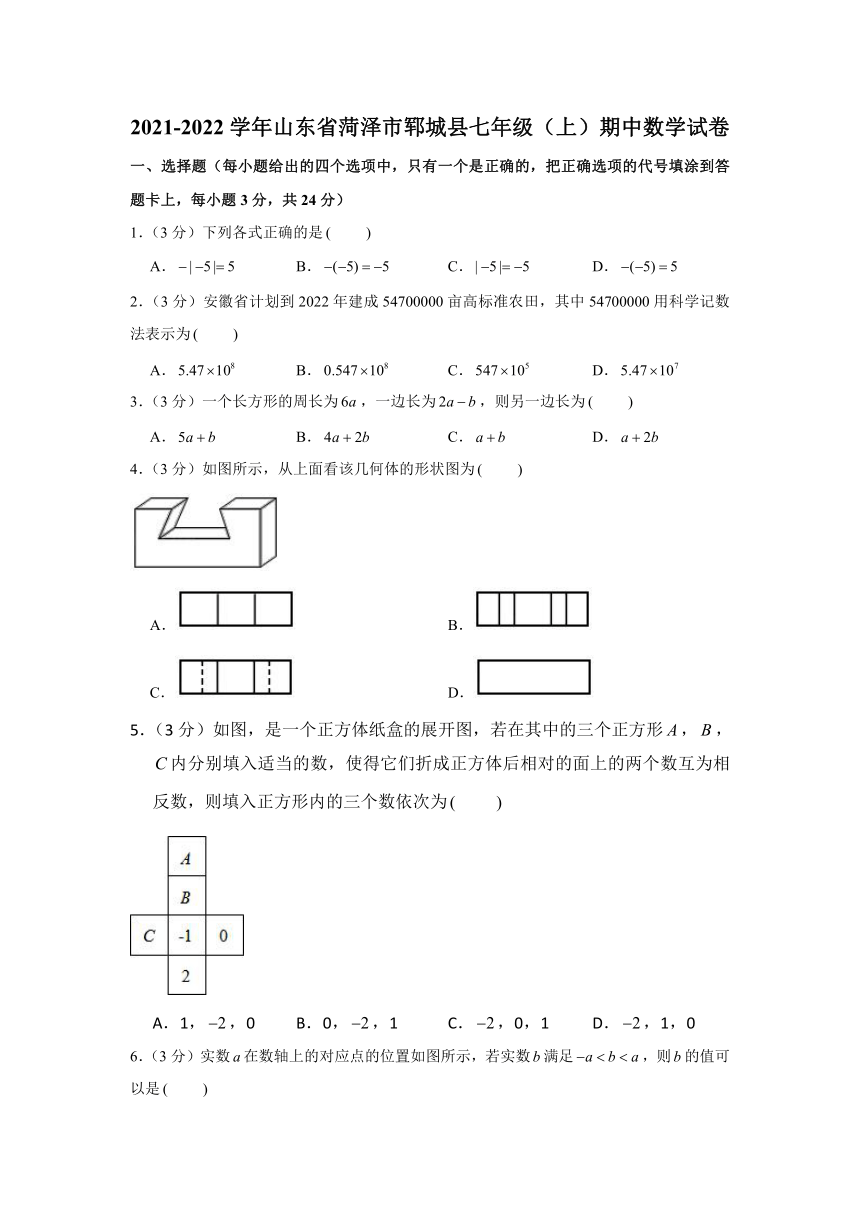 | |
| 格式 | docx | ||
| 文件大小 | 699.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 07:05:42 | ||
图片预览





文档简介
2021-2022学年山东省菏泽市郓城县七年级(上)期中数学试卷
一、选择题(每小题给出的四个选项中,只有一个是正确的,把正确选项的代号填涂到答题卡上,每小题3分,共24分)
1.(3分)下列各式正确的是
A. B. C. D.
2.(3分)安徽省计划到2022年建成54700000亩高标准农田,其中54700000用科学记数法表示为
A. B. C. D.
3.(3分)一个长方形的周长为,一边长为,则另一边长为
A. B. C. D.
4.(3分)如图所示,从上面看该几何体的形状图为
A. B.
C. D.
5.(3分)如图,是一个正方体纸盒的展开图,若在其中的三个正方形,,内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形内的三个数依次为
A.1,,0 B.0,,1 C.,0,1 D.,1,0
6.(3分)实数在数轴上的对应点的位置如图所示,若实数满足,则的值可以是
A.2 B. C. D.
7.(3分)某商店举办促销活动,促销的方法是将原价元的衣服以元出售,则下列说法中,能正确表达该商店促销方法的是
A.原价减去10元后再打8折 B.原价打8折后再减去10元
C.原价减去10元后再打2折 D.原价打2折后再减去10元
8.(3分)按一定规律排列的单项式:,,,,,,,第个单项式是
A. B. C. D.
二、填空题(每小题3分,共18分)
9.(3分)薄薄的硬币在桌面上转动时,看上去像球,由此说明了 的数学事实.
10.(3分)数轴上点表示的数是,将点在数轴上平移7个单位长度得到点,则平移后点表示的数是 .
11.(3分)用小立方体搭一个几何体,分别从它的正面、上面看到的形状如图所示.这样的几何体最少需要 个小立方体;最多需要 个小立方体.
12.(3分)一瓶500毫升的饮料,每次喝掉瓶内饮品的一半,如此喝下去,第六次喝完之后瓶内剩下的饮品为 毫升.
13.(3分)若单项式的和是单项式,则 .
14.(3分)当时,代数式的值为3,则 .
三、解答题(共78分,解答要写出必要的文字说明、演算步骤)
15.(6分)一个几何体由若干个相同的小正方体组成,如图是从上面看得到的图形,其中每个小正方形中的数字代表该位置小正方体的个数,请画出该几何体从正面和从左面看得到的图形.
16.(6分)如图,是一个几何体的平面展开图;
(1)这个几何体是 ;
(2)求这个几何体的体积.取
17.(6分)我们知道,三棱柱的上、下底面都是三角形,那么正三棱柱的上、下底面都是等边三角形,如图,大正三棱柱的高为10,截取一个底面周长为3的小正三棱柱.
(1)请写出截面的形状;
(2)请计算截面的面积.
18.(6分)已知:,,且,求的值.
19.(12分)计算:
(1);
(2);
(3);
(4).
20.(8分)已知蜗牛从点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“”,向负半轴运动记作“”,从开始到结束爬行的各段路程(单位:依次为:,,,,,,,
(1)若点在数轴上表示的数为,则蜗牛停在数轴上何处,请通过计算加以说明;
(2)若蜗牛的爬行速度为每秒,请问蜗牛一共爬行了多少秒?
21.(8分)(1)已知多项式是六次四项式,单项式的次数与多项式的次数相同,求,的值;
(2)已知多项式不含和的项,试写出这个多项式,再求当时多项式的值.
22.(8分)先化简,再求值:
(1),其中,;
(2),其中,.
23.(8分)如图所示,在长为,宽为的长方形中减去一个直角边为的等腰直角三角形和直径为的半圆.
(1)用含,的式子表示阴影部分的面积;
(2)当,时,求阴影部分的面积.取
24.(10分)下列图形是用棋子摆成的“上”字,如果按照此规律继续摆下去:
(1)图4中的“上”字需要用 枚棋子.图5中的“上”字需要用 枚棋子;
(2)图中的“上”字需要用 枚棋子;
(3)现有62名学生,把每一位学生当成一枚棋子,能否让这62枚“棋子”按照以上规律恰好站成一个“上”字?若能,请直接写出最下面一“横”的学生数,若不能,请说明理由.
参考答案与解析
一、选择题(每小题给出的四个选项中,只有一个是正确的,把正确选项的代号填涂到答题卡上,每小题3分,共24分)
1.(3分)下列各式正确的是
A. B. C. D.
【解答】解:、,
选项不符合题意;
、,
选项不符合题意;
、,
选项不符合题意;
、,
选项符合题意.
故选:.
2.(3分)安徽省计划到2022年建成54700000亩高标准农田,其中54700000用科学记数法表示为
A. B. C. D.
【解答】解:54700000用科学记数法表示为:.
故选:.
3.(3分)一个长方形的周长为,一边长为,则另一边长为
A. B. C. D.
【解答】解:根据题意得:
.
故选:.
4.(3分)如图所示,从上面看该几何体的形状图为
A. B.
C. D.
【解答】解:根据能看见的轮廓线用实线表示,看不见的轮廓线用虚线表示,
从上面看到的是矩形,且有看不见的轮廓线,
因此选项中的图形符合题意;
故选:.
5.(3分)如图,是一个正方体纸盒的展开图,若在其中的三个正方形,,内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形内的三个数依次为
A.1,,0 B.0,,1 C.,0,1 D.,1,0
【解答】解:由图可知对应,对应2,对应0.
的相反数为1,2的相反数为,0的相反数为0,
,,.
故选:.
6.(3分)实数在数轴上的对应点的位置如图所示,若实数满足,则的值可以是
A.2 B. C. D.
【解答】解:因为,
所以,
因为,
所以只能是.
故选:.
7.(3分)某商店举办促销活动,促销的方法是将原价元的衣服以元出售,则下列说法中,能正确表达该商店促销方法的是
A.原价减去10元后再打8折 B.原价打8折后再减去10元
C.原价减去10元后再打2折 D.原价打2折后再减去10元
【解答】解:根据分析,可得
将原价元的衣服以元出售,
是把原价打8折后再减去10元.
故选:.
8.(3分)按一定规律排列的单项式:,,,,,,,第个单项式是
A. B. C. D.
【解答】解:,
,
,
,
,
,
由上规律可知,第个单项式为:.
故选:.
二、填空题(每小题3分,共18分)
9.(3分)薄薄的硬币在桌面上转动时,看上去像球,由此说明了 面动成体 的数学事实.
【解答】解:“薄薄的硬币”可以近似看作“圆形的面”,薄薄的硬币在桌面上转动时,看上去像球,说明了“面动成体”,
故答案为:面动成体.
10.(3分)数轴上点表示的数是,将点在数轴上平移7个单位长度得到点,则平移后点表示的数是 4或 .
【解答】如果向右平移: 如果向左平移:
故填4或
11.(3分)用小立方体搭一个几何体,分别从它的正面、上面看到的形状如图所示.这样的几何体最少需要 9 个小立方体;最多需要 个小立方体.
【解答】解:不止一种.最少需要个小正方体,最多需要个小正方体,
故答案为:9;12.
12.(3分)一瓶500毫升的饮料,每次喝掉瓶内饮品的一半,如此喝下去,第六次喝完之后瓶内剩下的饮品为 7.8125 毫升.
【解答】解:(毫升).
故答案为:7.8125.
13.(3分)若单项式的和是单项式,则 9 .
【解答】解:单项式的和是单项式,
且,
解得:,,
,
故答案为:9.
14.(3分)当时,代数式的值为3,则 34 .
【解答】解:时,代数式的值为3,
,
即,
,
故答案为:34.
三、解答题(共78分,解答要写出必要的文字说明、演算步骤)
15.(6分)一个几何体由若干个相同的小正方体组成,如图是从上面看得到的图形,其中每个小正方形中的数字代表该位置小正方体的个数,请画出该几何体从正面和从左面看得到的图形.
【解答】解:从正面看和从左面看得到的图形如图所示.
.
16.(6分)如图,是一个几何体的平面展开图;
(1)这个几何体是 圆柱 ;
(2)求这个几何体的体积.取
【解答】解:(1)几何体的展开图侧面是矩形,两底面是圆形,
几何体是圆柱,
故答案为:圆柱;
(2)体积:,
答:这个几何体的体积是.
17.(6分)我们知道,三棱柱的上、下底面都是三角形,那么正三棱柱的上、下底面都是等边三角形,如图,大正三棱柱的高为10,截取一个底面周长为3的小正三棱柱.
(1)请写出截面的形状;
(2)请计算截面的面积.
【解答】解:(1)由图可得截面的形状为长方形;
(2)小正三棱柱的底面周长为3,
底面边长,
截面的面积.
18.(6分)已知:,,且,求的值.
【解答】解:,
,
,
,
又,
,.
或.
19.(12分)计算:
(1);
(2);
(3);
(4).
【解答】解:(1)
;
(2)
;
(3)
;
(4)
.
20.(8分)已知蜗牛从点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“”,向负半轴运动记作“”,从开始到结束爬行的各段路程(单位:依次为:,,,,,,,
(1)若点在数轴上表示的数为,则蜗牛停在数轴上何处,请通过计算加以说明;
(2)若蜗牛的爬行速度为每秒,请问蜗牛一共爬行了多少秒?
【解答】解:(1)依题意得
,
蜗牛停在数轴上的原点;
(2)秒.
蜗牛一共爬行了122秒.
21.(8分)(1)已知多项式是六次四项式,单项式的次数与多项式的次数相同,求,的值;
(2)已知多项式不含和的项,试写出这个多项式,再求当时多项式的值.
【解答】解:(1)由题意得:;,
解得:,;
(2)多项式不含和的项,
,,
解得:,,即多项式为,
当时,原式.
22.(8分)先化简,再求值:
(1),其中,;
(2),其中,.
【解答】解:(1)原式
,
,
当,时,
原式
;
(2)原式
,
当,时,
原式
.
23.(8分)如图所示,在长为,宽为的长方形中减去一个直角边为的等腰直角三角形和直径为的半圆.
(1)用含,的式子表示阴影部分的面积;
(2)当,时,求阴影部分的面积.取
【解答】解:(1)根据题意,得:
阴影部分的面积长方形的面积等腰直角三角形的面积半圆的面积,
长方形的面积,
等腰直角三角形的面积,
半圆的面积,
故阴影部分的面积为:.
(2)当,时,.
24.(10分)下列图形是用棋子摆成的“上”字,如果按照此规律继续摆下去:
(1)图4中的“上”字需要用 18 枚棋子.图5中的“上”字需要用 枚棋子;
(2)图中的“上”字需要用 枚棋子;
(3)现有62名学生,把每一位学生当成一枚棋子,能否让这62枚“棋子”按照以上规律恰好站成一个“上”字?若能,请直接写出最下面一“横”的学生数,若不能,请说明理由.
【解答】解:(1)第①个图形中有6个棋子;
第②个图形中有个棋子;
第③个图形中有个棋子;
第④个图形中有个棋子,
第⑤个图形中有个棋子.
故答案为:18、22;
(2)第个图形中有.
故答案为:.
(3)能,最小面一横的学生人数为31人,理由如下:
,
解得.
最下一横人数为.
一、选择题(每小题给出的四个选项中,只有一个是正确的,把正确选项的代号填涂到答题卡上,每小题3分,共24分)
1.(3分)下列各式正确的是
A. B. C. D.
2.(3分)安徽省计划到2022年建成54700000亩高标准农田,其中54700000用科学记数法表示为
A. B. C. D.
3.(3分)一个长方形的周长为,一边长为,则另一边长为
A. B. C. D.
4.(3分)如图所示,从上面看该几何体的形状图为
A. B.
C. D.
5.(3分)如图,是一个正方体纸盒的展开图,若在其中的三个正方形,,内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形内的三个数依次为
A.1,,0 B.0,,1 C.,0,1 D.,1,0
6.(3分)实数在数轴上的对应点的位置如图所示,若实数满足,则的值可以是
A.2 B. C. D.
7.(3分)某商店举办促销活动,促销的方法是将原价元的衣服以元出售,则下列说法中,能正确表达该商店促销方法的是
A.原价减去10元后再打8折 B.原价打8折后再减去10元
C.原价减去10元后再打2折 D.原价打2折后再减去10元
8.(3分)按一定规律排列的单项式:,,,,,,,第个单项式是
A. B. C. D.
二、填空题(每小题3分,共18分)
9.(3分)薄薄的硬币在桌面上转动时,看上去像球,由此说明了 的数学事实.
10.(3分)数轴上点表示的数是,将点在数轴上平移7个单位长度得到点,则平移后点表示的数是 .
11.(3分)用小立方体搭一个几何体,分别从它的正面、上面看到的形状如图所示.这样的几何体最少需要 个小立方体;最多需要 个小立方体.
12.(3分)一瓶500毫升的饮料,每次喝掉瓶内饮品的一半,如此喝下去,第六次喝完之后瓶内剩下的饮品为 毫升.
13.(3分)若单项式的和是单项式,则 .
14.(3分)当时,代数式的值为3,则 .
三、解答题(共78分,解答要写出必要的文字说明、演算步骤)
15.(6分)一个几何体由若干个相同的小正方体组成,如图是从上面看得到的图形,其中每个小正方形中的数字代表该位置小正方体的个数,请画出该几何体从正面和从左面看得到的图形.
16.(6分)如图,是一个几何体的平面展开图;
(1)这个几何体是 ;
(2)求这个几何体的体积.取
17.(6分)我们知道,三棱柱的上、下底面都是三角形,那么正三棱柱的上、下底面都是等边三角形,如图,大正三棱柱的高为10,截取一个底面周长为3的小正三棱柱.
(1)请写出截面的形状;
(2)请计算截面的面积.
18.(6分)已知:,,且,求的值.
19.(12分)计算:
(1);
(2);
(3);
(4).
20.(8分)已知蜗牛从点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“”,向负半轴运动记作“”,从开始到结束爬行的各段路程(单位:依次为:,,,,,,,
(1)若点在数轴上表示的数为,则蜗牛停在数轴上何处,请通过计算加以说明;
(2)若蜗牛的爬行速度为每秒,请问蜗牛一共爬行了多少秒?
21.(8分)(1)已知多项式是六次四项式,单项式的次数与多项式的次数相同,求,的值;
(2)已知多项式不含和的项,试写出这个多项式,再求当时多项式的值.
22.(8分)先化简,再求值:
(1),其中,;
(2),其中,.
23.(8分)如图所示,在长为,宽为的长方形中减去一个直角边为的等腰直角三角形和直径为的半圆.
(1)用含,的式子表示阴影部分的面积;
(2)当,时,求阴影部分的面积.取
24.(10分)下列图形是用棋子摆成的“上”字,如果按照此规律继续摆下去:
(1)图4中的“上”字需要用 枚棋子.图5中的“上”字需要用 枚棋子;
(2)图中的“上”字需要用 枚棋子;
(3)现有62名学生,把每一位学生当成一枚棋子,能否让这62枚“棋子”按照以上规律恰好站成一个“上”字?若能,请直接写出最下面一“横”的学生数,若不能,请说明理由.
参考答案与解析
一、选择题(每小题给出的四个选项中,只有一个是正确的,把正确选项的代号填涂到答题卡上,每小题3分,共24分)
1.(3分)下列各式正确的是
A. B. C. D.
【解答】解:、,
选项不符合题意;
、,
选项不符合题意;
、,
选项不符合题意;
、,
选项符合题意.
故选:.
2.(3分)安徽省计划到2022年建成54700000亩高标准农田,其中54700000用科学记数法表示为
A. B. C. D.
【解答】解:54700000用科学记数法表示为:.
故选:.
3.(3分)一个长方形的周长为,一边长为,则另一边长为
A. B. C. D.
【解答】解:根据题意得:
.
故选:.
4.(3分)如图所示,从上面看该几何体的形状图为
A. B.
C. D.
【解答】解:根据能看见的轮廓线用实线表示,看不见的轮廓线用虚线表示,
从上面看到的是矩形,且有看不见的轮廓线,
因此选项中的图形符合题意;
故选:.
5.(3分)如图,是一个正方体纸盒的展开图,若在其中的三个正方形,,内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形内的三个数依次为
A.1,,0 B.0,,1 C.,0,1 D.,1,0
【解答】解:由图可知对应,对应2,对应0.
的相反数为1,2的相反数为,0的相反数为0,
,,.
故选:.
6.(3分)实数在数轴上的对应点的位置如图所示,若实数满足,则的值可以是
A.2 B. C. D.
【解答】解:因为,
所以,
因为,
所以只能是.
故选:.
7.(3分)某商店举办促销活动,促销的方法是将原价元的衣服以元出售,则下列说法中,能正确表达该商店促销方法的是
A.原价减去10元后再打8折 B.原价打8折后再减去10元
C.原价减去10元后再打2折 D.原价打2折后再减去10元
【解答】解:根据分析,可得
将原价元的衣服以元出售,
是把原价打8折后再减去10元.
故选:.
8.(3分)按一定规律排列的单项式:,,,,,,,第个单项式是
A. B. C. D.
【解答】解:,
,
,
,
,
,
由上规律可知,第个单项式为:.
故选:.
二、填空题(每小题3分,共18分)
9.(3分)薄薄的硬币在桌面上转动时,看上去像球,由此说明了 面动成体 的数学事实.
【解答】解:“薄薄的硬币”可以近似看作“圆形的面”,薄薄的硬币在桌面上转动时,看上去像球,说明了“面动成体”,
故答案为:面动成体.
10.(3分)数轴上点表示的数是,将点在数轴上平移7个单位长度得到点,则平移后点表示的数是 4或 .
【解答】如果向右平移: 如果向左平移:
故填4或
11.(3分)用小立方体搭一个几何体,分别从它的正面、上面看到的形状如图所示.这样的几何体最少需要 9 个小立方体;最多需要 个小立方体.
【解答】解:不止一种.最少需要个小正方体,最多需要个小正方体,
故答案为:9;12.
12.(3分)一瓶500毫升的饮料,每次喝掉瓶内饮品的一半,如此喝下去,第六次喝完之后瓶内剩下的饮品为 7.8125 毫升.
【解答】解:(毫升).
故答案为:7.8125.
13.(3分)若单项式的和是单项式,则 9 .
【解答】解:单项式的和是单项式,
且,
解得:,,
,
故答案为:9.
14.(3分)当时,代数式的值为3,则 34 .
【解答】解:时,代数式的值为3,
,
即,
,
故答案为:34.
三、解答题(共78分,解答要写出必要的文字说明、演算步骤)
15.(6分)一个几何体由若干个相同的小正方体组成,如图是从上面看得到的图形,其中每个小正方形中的数字代表该位置小正方体的个数,请画出该几何体从正面和从左面看得到的图形.
【解答】解:从正面看和从左面看得到的图形如图所示.
.
16.(6分)如图,是一个几何体的平面展开图;
(1)这个几何体是 圆柱 ;
(2)求这个几何体的体积.取
【解答】解:(1)几何体的展开图侧面是矩形,两底面是圆形,
几何体是圆柱,
故答案为:圆柱;
(2)体积:,
答:这个几何体的体积是.
17.(6分)我们知道,三棱柱的上、下底面都是三角形,那么正三棱柱的上、下底面都是等边三角形,如图,大正三棱柱的高为10,截取一个底面周长为3的小正三棱柱.
(1)请写出截面的形状;
(2)请计算截面的面积.
【解答】解:(1)由图可得截面的形状为长方形;
(2)小正三棱柱的底面周长为3,
底面边长,
截面的面积.
18.(6分)已知:,,且,求的值.
【解答】解:,
,
,
,
又,
,.
或.
19.(12分)计算:
(1);
(2);
(3);
(4).
【解答】解:(1)
;
(2)
;
(3)
;
(4)
.
20.(8分)已知蜗牛从点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“”,向负半轴运动记作“”,从开始到结束爬行的各段路程(单位:依次为:,,,,,,,
(1)若点在数轴上表示的数为,则蜗牛停在数轴上何处,请通过计算加以说明;
(2)若蜗牛的爬行速度为每秒,请问蜗牛一共爬行了多少秒?
【解答】解:(1)依题意得
,
蜗牛停在数轴上的原点;
(2)秒.
蜗牛一共爬行了122秒.
21.(8分)(1)已知多项式是六次四项式,单项式的次数与多项式的次数相同,求,的值;
(2)已知多项式不含和的项,试写出这个多项式,再求当时多项式的值.
【解答】解:(1)由题意得:;,
解得:,;
(2)多项式不含和的项,
,,
解得:,,即多项式为,
当时,原式.
22.(8分)先化简,再求值:
(1),其中,;
(2),其中,.
【解答】解:(1)原式
,
,
当,时,
原式
;
(2)原式
,
当,时,
原式
.
23.(8分)如图所示,在长为,宽为的长方形中减去一个直角边为的等腰直角三角形和直径为的半圆.
(1)用含,的式子表示阴影部分的面积;
(2)当,时,求阴影部分的面积.取
【解答】解:(1)根据题意,得:
阴影部分的面积长方形的面积等腰直角三角形的面积半圆的面积,
长方形的面积,
等腰直角三角形的面积,
半圆的面积,
故阴影部分的面积为:.
(2)当,时,.
24.(10分)下列图形是用棋子摆成的“上”字,如果按照此规律继续摆下去:
(1)图4中的“上”字需要用 18 枚棋子.图5中的“上”字需要用 枚棋子;
(2)图中的“上”字需要用 枚棋子;
(3)现有62名学生,把每一位学生当成一枚棋子,能否让这62枚“棋子”按照以上规律恰好站成一个“上”字?若能,请直接写出最下面一“横”的学生数,若不能,请说明理由.
【解答】解:(1)第①个图形中有6个棋子;
第②个图形中有个棋子;
第③个图形中有个棋子;
第④个图形中有个棋子,
第⑤个图形中有个棋子.
故答案为:18、22;
(2)第个图形中有.
故答案为:.
(3)能,最小面一横的学生人数为31人,理由如下:
,
解得.
最下一横人数为.
同课章节目录
