六年级数学下册课件-3 解决问题的策略 苏教版(共43张PPT)
文档属性
| 名称 | 六年级数学下册课件-3 解决问题的策略 苏教版(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 06:18:17 | ||
图片预览










文档简介
(共43张PPT)
2、解决问题的策略(2)
+ = 36
= + +
=( ) = ( )
1头牛的重量相当于2头猪的重量,1头猪的重量相当于3只羊的重量,2头牛的重量相当于( )羊的重量。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
你准备用什么方法来解决这个问题?
例2
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
画图法
列举法
假设法
画图法
先画10只大船坐50人,再去掉多的8人。
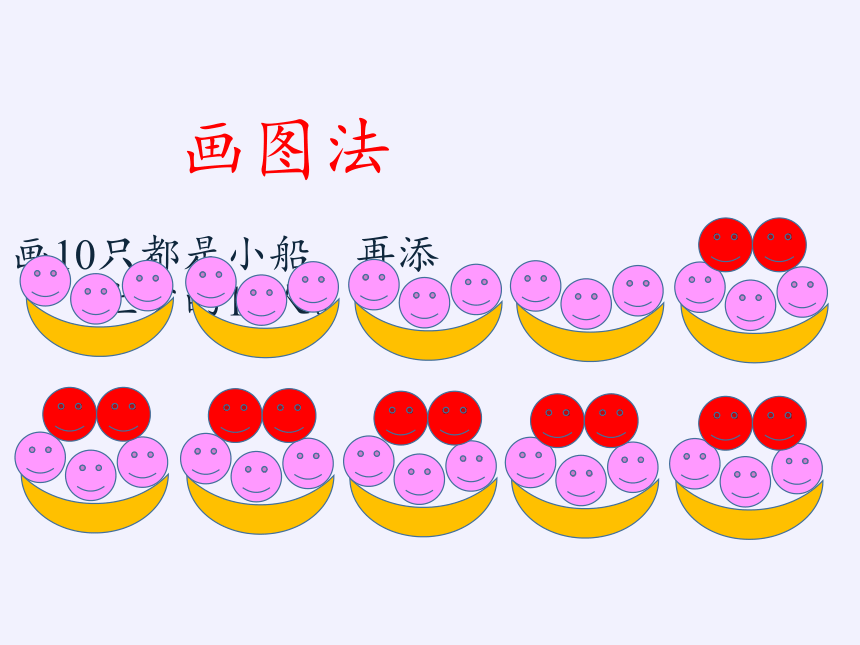
画图法
画10只都是小船,再添上少的12人。
此时得出大船有6只,小船有4只。
列举法
大船只数 小船只数 乘坐的总人数 和42人比较
大船 只数 小船 只数 总人数 和42人 比较
5 5 5×5+3×5=40 少2人
5×6+3×4=42
相等
假设5只是大船,5只是小船:
通过比较假设后的人数和实际人数,推算出大船和小船的只数。
4
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
假设法
例2
假设10只都是大船。
假设10只都是小船。
假设5只小船,5只大船。
假设10只都是大船:
1. 一共坐多少人?
5×10=50(人)
50-42=8(人)
2. 还要把多少只大船改成小船?
小船:8÷(5-3) =4(只)
假设10只船都是小船呢
大船:10-4=6(只)
多了多少人?
1. 10只小船能坐多少人?还少多少人?
2. 为什么会少呢?
3. 还要把多少只小船改成大船?
假设10只都是小船:
假设10只都是小船:
10只小船能坐多少人?还少多少人?
还要把多少只小船改成大船?
10×3=30(人)
42-30=12(人)
12÷(5—3)=6(只)
小船:
10-6=4(只)
大船:
如果假设小船和大船各一半呢?
小船和大船乘坐总人数:
5×3 + 5×5 = 40(人)
还有多少人?
42-40 = 2(人)
还需要把几只小船改成大船?
2÷(5-3)=1(只)
由此得出:大船5+1=6(只) 小船5-1=4 (只)
我们可以如何检验结果是否正确呢?
检验人数和船只数。
5×6+3×4=42(人)
答:租用的大船有6只,租用的小船有4只。
6+4=10(只)
画图
列举
假设
用画图、列举和假设策略解决问题时有什么类似的地方?
1、先看成几只大船或者几只小船。
2、按大船和小船每只相差2人调整。
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?(根据小面的提示,选择一种方法找出答案)
(1)画8个圆,表示一共有8只动物。
(2)先假设,根据假设给每只动物画上腿,算出画的腿比实际多(或少)几条。
(3)怎样进行调整。
(4)写出计算过程,并检验。
1. 画8个圆表示8只动物。
2. 假设8只都是鸡。每个动物有几条腿?一共有多少条腿?
3. 比实际少几条腿?每只兔补几条腿?
22-16=6(条)
6÷2=3(只)
说明兔有多少只?
4. 鸡有多少只?
8-3=5(只)
2×8=16(条)
1. 假设8只全是兔?一共有多少条腿?
4×8=32(条)
2. 比实际多出多少条腿?
32-22=10(条)
3. 每只鸡要少2条腿?多少只鸡正好少了10条腿?
10÷2=5(只)
4. 兔有多少只?
8-5=3(只)
假设鸡和兔同样多,再调整。
鸡的只数 兔的只数 腿的总条数 和22条比较
4 4
5 3
4×2+4×4=24
多2条
刚好
5×2+3×4=22
练习五
4、六年级同学制作了78件蝴蝶标本,帖在9块展板上展出。
两种展板各有多少块?
每块小展板贴6件,每块大展板贴10件。
大展板块数 小展板块数 蝴蝶标本总件数 和78件比较
5 4 5×10+4×6=74 少了4件
6
3
6×10+3×6=78
刚好
假设两种展板的块数,计算标本总件数,再进行调整。
5.
1元和5角的硬币一共
13枚,共有10元。
1元和5角的硬币
各有多少枚。
1元的枚数 5角的枚数 总元数 和10元比较
5.
1元和5角的硬币一共
13枚,共有10元。
1元和5角的硬币
各有多少枚。
一百馒头一百僧,大僧三个更无增;小僧三人分一个,大小和尚各几丁?
明代大数学家程大位著的《算法统宗》中有这样一题:
100个和尚吃100个馒头。
大和尚一人吃三个,
小和尚三人吃一个。
大、小和尚各多少人?
据题意可知,1个大和尚和3个小和尚一共吃4个馒头,也就是说,每4个馒头,就正好分给1个大和尚和3个小和尚。我们不妨把100个馒头每4个分为一组,共可分:100÷4=25(组),而100个和尚也正好分为这样的25组,在每组中,必有1个大和尚、3个小和尚,于是可很方便地求得答案。
大和尚共有:1×25=25(个)
小和尚共有:3×25=75(个)
假设大和尚100人
100×3=300(个)
300-100=200(个)
200÷(3- )=75(个)
100-75=25(个)
答:大和尚25人,小和尚75人。
设大和尚x人,小和尚(100-x)人.
3x+(100-X)÷3=100
9x+100-x=300
8x=200
x=25
100-25=75
同学们,这节课你学习了那些策略?主要学会了什么策略呢?
回顾解决问题的过程,你有什么体会?
画图、列举、先假设再调整都是解决问题的有效策略。
分析和解决同一个问题,可以用不同的策略。
要学会根据具体问题灵活选择策略。
《孙子算经》中的鸡兔同笼问题
大约在一千五百年前,大数学家孙子在《孙子算经》中记载了这样的一道题:“今有雏兔同笼,上有三十五头,下有九十四足,问雏兔各几何?”这四句的意思就是:有若干只鸡和兔在同一个笼子里,从上面数,有三十五个头;从下面数,有九十四只脚。求笼中各有几只鸡和兔?
有若干只鸡和兔在同一个笼子里,从上面数,有三十五个头;从下面数,有九十四只脚。求笼中各有几只鸡和兔?
作业:课本31页
练习五 第6、7题
谢 谢
2、解决问题的策略(2)
+ = 36
= + +
=( ) = ( )
1头牛的重量相当于2头猪的重量,1头猪的重量相当于3只羊的重量,2头牛的重量相当于( )羊的重量。
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
你准备用什么方法来解决这个问题?
例2
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
画图法
列举法
假设法
画图法
先画10只大船坐50人,再去掉多的8人。
画图法
画10只都是小船,再添上少的12人。
此时得出大船有6只,小船有4只。
列举法
大船只数 小船只数 乘坐的总人数 和42人比较
大船 只数 小船 只数 总人数 和42人 比较
5 5 5×5+3×5=40 少2人
5×6+3×4=42
相等
假设5只是大船,5只是小船:
通过比较假设后的人数和实际人数,推算出大船和小船的只数。
4
全班42人去公园划船,租10只船正好坐满。每只大船坐5人,每只小船坐3人。租的大船、小船各有多少只?
假设法
例2
假设10只都是大船。
假设10只都是小船。
假设5只小船,5只大船。
假设10只都是大船:
1. 一共坐多少人?
5×10=50(人)
50-42=8(人)
2. 还要把多少只大船改成小船?
小船:8÷(5-3) =4(只)
假设10只船都是小船呢
大船:10-4=6(只)
多了多少人?
1. 10只小船能坐多少人?还少多少人?
2. 为什么会少呢?
3. 还要把多少只小船改成大船?
假设10只都是小船:
假设10只都是小船:
10只小船能坐多少人?还少多少人?
还要把多少只小船改成大船?
10×3=30(人)
42-30=12(人)
12÷(5—3)=6(只)
小船:
10-6=4(只)
大船:
如果假设小船和大船各一半呢?
小船和大船乘坐总人数:
5×3 + 5×5 = 40(人)
还有多少人?
42-40 = 2(人)
还需要把几只小船改成大船?
2÷(5-3)=1(只)
由此得出:大船5+1=6(只) 小船5-1=4 (只)
我们可以如何检验结果是否正确呢?
检验人数和船只数。
5×6+3×4=42(人)
答:租用的大船有6只,租用的小船有4只。
6+4=10(只)
画图
列举
假设
用画图、列举和假设策略解决问题时有什么类似的地方?
1、先看成几只大船或者几只小船。
2、按大船和小船每只相差2人调整。
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?
鸡和兔一共有8只,它们的腿有22条。鸡和兔各有多少只?(根据小面的提示,选择一种方法找出答案)
(1)画8个圆,表示一共有8只动物。
(2)先假设,根据假设给每只动物画上腿,算出画的腿比实际多(或少)几条。
(3)怎样进行调整。
(4)写出计算过程,并检验。
1. 画8个圆表示8只动物。
2. 假设8只都是鸡。每个动物有几条腿?一共有多少条腿?
3. 比实际少几条腿?每只兔补几条腿?
22-16=6(条)
6÷2=3(只)
说明兔有多少只?
4. 鸡有多少只?
8-3=5(只)
2×8=16(条)
1. 假设8只全是兔?一共有多少条腿?
4×8=32(条)
2. 比实际多出多少条腿?
32-22=10(条)
3. 每只鸡要少2条腿?多少只鸡正好少了10条腿?
10÷2=5(只)
4. 兔有多少只?
8-5=3(只)
假设鸡和兔同样多,再调整。
鸡的只数 兔的只数 腿的总条数 和22条比较
4 4
5 3
4×2+4×4=24
多2条
刚好
5×2+3×4=22
练习五
4、六年级同学制作了78件蝴蝶标本,帖在9块展板上展出。
两种展板各有多少块?
每块小展板贴6件,每块大展板贴10件。
大展板块数 小展板块数 蝴蝶标本总件数 和78件比较
5 4 5×10+4×6=74 少了4件
6
3
6×10+3×6=78
刚好
假设两种展板的块数,计算标本总件数,再进行调整。
5.
1元和5角的硬币一共
13枚,共有10元。
1元和5角的硬币
各有多少枚。
1元的枚数 5角的枚数 总元数 和10元比较
5.
1元和5角的硬币一共
13枚,共有10元。
1元和5角的硬币
各有多少枚。
一百馒头一百僧,大僧三个更无增;小僧三人分一个,大小和尚各几丁?
明代大数学家程大位著的《算法统宗》中有这样一题:
100个和尚吃100个馒头。
大和尚一人吃三个,
小和尚三人吃一个。
大、小和尚各多少人?
据题意可知,1个大和尚和3个小和尚一共吃4个馒头,也就是说,每4个馒头,就正好分给1个大和尚和3个小和尚。我们不妨把100个馒头每4个分为一组,共可分:100÷4=25(组),而100个和尚也正好分为这样的25组,在每组中,必有1个大和尚、3个小和尚,于是可很方便地求得答案。
大和尚共有:1×25=25(个)
小和尚共有:3×25=75(个)
假设大和尚100人
100×3=300(个)
300-100=200(个)
200÷(3- )=75(个)
100-75=25(个)
答:大和尚25人,小和尚75人。
设大和尚x人,小和尚(100-x)人.
3x+(100-X)÷3=100
9x+100-x=300
8x=200
x=25
100-25=75
同学们,这节课你学习了那些策略?主要学会了什么策略呢?
回顾解决问题的过程,你有什么体会?
画图、列举、先假设再调整都是解决问题的有效策略。
分析和解决同一个问题,可以用不同的策略。
要学会根据具体问题灵活选择策略。
《孙子算经》中的鸡兔同笼问题
大约在一千五百年前,大数学家孙子在《孙子算经》中记载了这样的一道题:“今有雏兔同笼,上有三十五头,下有九十四足,问雏兔各几何?”这四句的意思就是:有若干只鸡和兔在同一个笼子里,从上面数,有三十五个头;从下面数,有九十四只脚。求笼中各有几只鸡和兔?
有若干只鸡和兔在同一个笼子里,从上面数,有三十五个头;从下面数,有九十四只脚。求笼中各有几只鸡和兔?
作业:课本31页
练习五 第6、7题
谢 谢
