沪科版数学八年级上册 15.1轴对称图形 课件(共35张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 15.1轴对称图形 课件(共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览









文档简介
(共35张PPT)
15.1 轴对称图形(1)
面对生活中这些美丽的图片,
你是否强烈地感受到美就在我们身边!
这是一种怎样的美呢
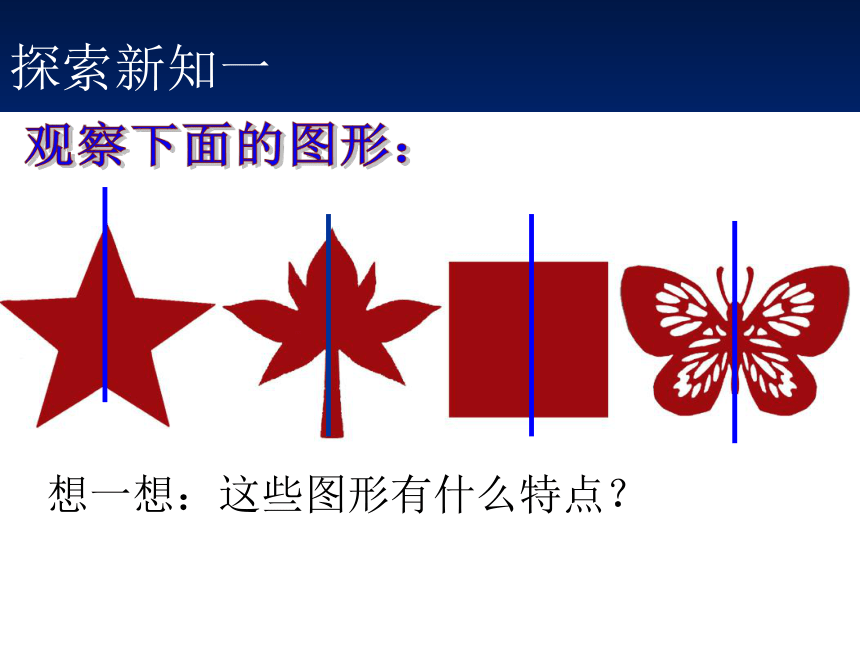
探索新知一
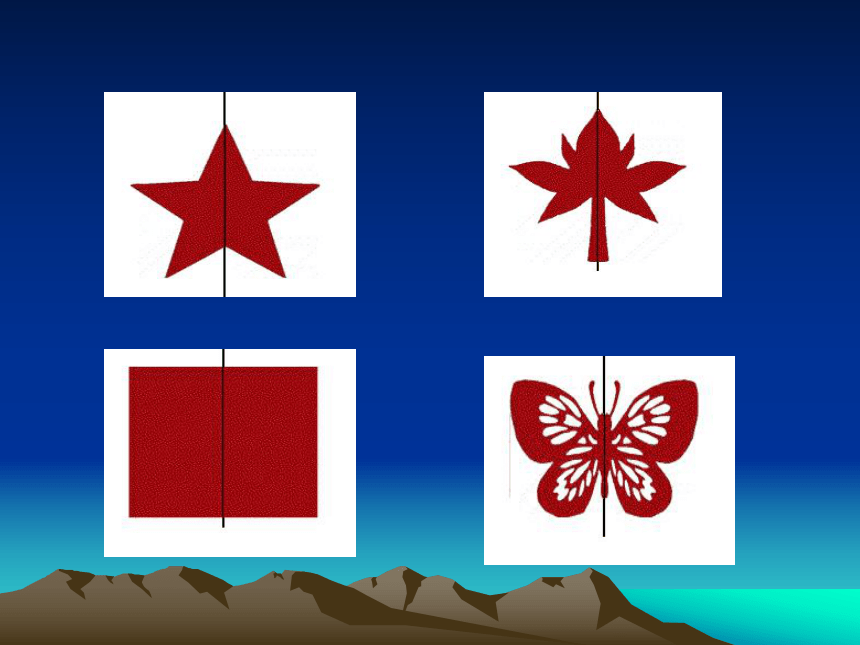
想一想:这些图形有什么特点?
轴对称图形:
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做
折痕所在的这条直线叫做
对称轴。
…………
轴对称图形。
…………
…………
…………
……
找出图中的轴对称图形,并说出轴对称图形对称轴的个数。
一般等腰三角形
等腰梯形
一般长方形
一般平行四边形
一般三角形
圆
一般梯形
线段
角
0 1 2 3 4 5 6 7 8 9
0
8
下列数字图片是轴对称图形吗?
A B C D E F G H M Q
A
D
C
H
E
M
下列字母图片是轴对称图形吗?
在艺术字中,有些汉字是轴对称的,你能猜一猜下列是哪些字的一半吗?
猜字游戏
A
B
C
观察:下面的每对图形有什么共同特点
探索新知二
A′
B′
C′
A′
B′
C′
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么称这两个图形成轴对称,这条直线就是对称轴,折叠后重合的点叫做对应点(也叫对称点)。
A′
A
B
C
B′
C′
例题:下列给出的每幅图形中的两个 图案成轴对称吗?
喜喜
FF
(A)
(D)
(C)
(B)
√
√
√
×
试一试:下列每组图形是否成轴对称?
(一)
(二)
(三)
(四)
√
√
×
×
(分组讨论)
1.成轴对称的两个图形全等吗 ( ) 全等的两个图形一定成轴对称吗?
2.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗 ( )这两个图形对称吗 ( )
全等
全等
对称
1.沿一条直线折叠,直线两旁的部分能够 .
2.都有 .
3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线成 ;如果把两个成轴对称的图形看成一个整体,那么这个图形就是 .
联系
个图形
个图形
区别
(两个图形成)轴对称
轴对称图形
一
两
完全重合
对称轴
轴对称
轴对称图形
说说轴对称图形与两个图形成轴对称的区别于联系
通过今天的学习,你有什么收获?
课堂小结
轴对称图形的概念:
1、轴对称图形:
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;折痕所在的这条直线叫做对称轴。
2、轴对称:
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,折叠后重合的两点叫做对应点(也叫做对称点)。
轴对称图形 (两个图形成)轴对称
区别 _个图形 _个图形
联系 1.沿一条直线折叠,直线两旁的部分能够____.
2.都有____.
3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线成___;如果把两个成轴对称的图形看成一个图形,那么这个图形就是____.
一
两
完全重合
对称轴
轴对称
轴对称图形
国家体育场鸟巢
游泳中心水立方
2008年北京奥运会国家体育场——“鸟巢”
教师寄语:
我们的生活当中到处都充满了美,只要我们有一双发现美和创造美的眼睛,我们的生活将会更加美好!
布置作业
1.课本120面第1题。
习题15.1第1、2、3题。
2.动手任意剪一个你喜欢的轴对称图形。
3.预习课本第121—124页。
15.1 轴对称图形(1)
面对生活中这些美丽的图片,
你是否强烈地感受到美就在我们身边!
这是一种怎样的美呢
探索新知一
想一想:这些图形有什么特点?
轴对称图形:
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做
折痕所在的这条直线叫做
对称轴。
…………
轴对称图形。
…………
…………
…………
……
找出图中的轴对称图形,并说出轴对称图形对称轴的个数。
一般等腰三角形
等腰梯形
一般长方形
一般平行四边形
一般三角形
圆
一般梯形
线段
角
0 1 2 3 4 5 6 7 8 9
0
8
下列数字图片是轴对称图形吗?
A B C D E F G H M Q
A
D
C
H
E
M
下列字母图片是轴对称图形吗?
在艺术字中,有些汉字是轴对称的,你能猜一猜下列是哪些字的一半吗?
猜字游戏
A
B
C
观察:下面的每对图形有什么共同特点
探索新知二
A′
B′
C′
A′
B′
C′
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么称这两个图形成轴对称,这条直线就是对称轴,折叠后重合的点叫做对应点(也叫对称点)。
A′
A
B
C
B′
C′
例题:下列给出的每幅图形中的两个 图案成轴对称吗?
喜喜
FF
(A)
(D)
(C)
(B)
√
√
√
×
试一试:下列每组图形是否成轴对称?
(一)
(二)
(三)
(四)
√
√
×
×
(分组讨论)
1.成轴对称的两个图形全等吗 ( ) 全等的两个图形一定成轴对称吗?
2.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形全等吗 ( )这两个图形对称吗 ( )
全等
全等
对称
1.沿一条直线折叠,直线两旁的部分能够 .
2.都有 .
3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线成 ;如果把两个成轴对称的图形看成一个整体,那么这个图形就是 .
联系
个图形
个图形
区别
(两个图形成)轴对称
轴对称图形
一
两
完全重合
对称轴
轴对称
轴对称图形
说说轴对称图形与两个图形成轴对称的区别于联系
通过今天的学习,你有什么收获?
课堂小结
轴对称图形的概念:
1、轴对称图形:
如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形;折痕所在的这条直线叫做对称轴。
2、轴对称:
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,折叠后重合的两点叫做对应点(也叫做对称点)。
轴对称图形 (两个图形成)轴对称
区别 _个图形 _个图形
联系 1.沿一条直线折叠,直线两旁的部分能够____.
2.都有____.
3.如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条直线成___;如果把两个成轴对称的图形看成一个图形,那么这个图形就是____.
一
两
完全重合
对称轴
轴对称
轴对称图形
国家体育场鸟巢
游泳中心水立方
2008年北京奥运会国家体育场——“鸟巢”
教师寄语:
我们的生活当中到处都充满了美,只要我们有一双发现美和创造美的眼睛,我们的生活将会更加美好!
布置作业
1.课本120面第1题。
习题15.1第1、2、3题。
2.动手任意剪一个你喜欢的轴对称图形。
3.预习课本第121—124页。
