沪科版数学九年级上册 第22章 相似形(通用)(课件)(共16张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 第22章 相似形(通用)(课件)(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 644.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 08:34:38 | ||
图片预览




文档简介
(共16张PPT)
第22章 相似形(通用)
已知,如图,在△ABC中,以它的边AB,AC为边分别在形外作等边三角形△ABD,ACE,连接BE,DC,求证:BE=DC. (课本8上第150页12题)
【母题重现】
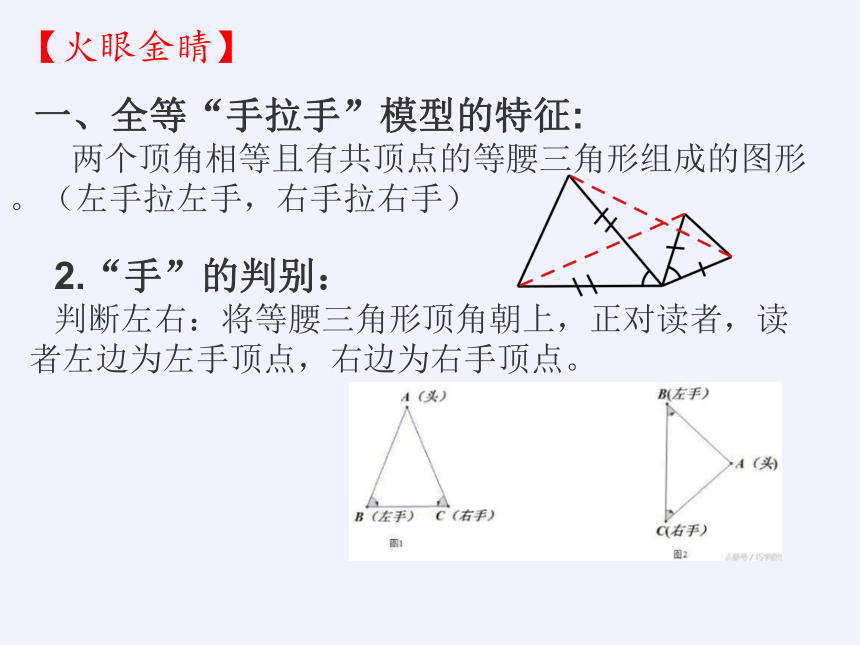
一、全等“手拉手”模型的特征:
两个顶角相等且有共顶点的等腰三角形组成的图形。(左手拉左手,右手拉右手)
2.“手”的判别:
判断左右:将等腰三角形顶角朝上,正对读者,读者左边为左手顶点,右边为右手顶点。
【火眼金睛】
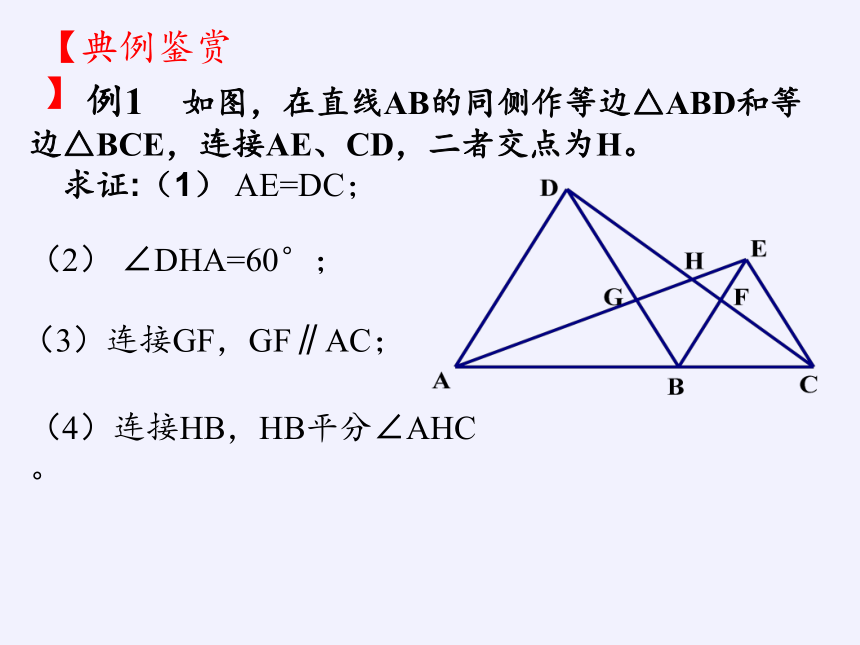
例1 如图,在直线AB的同侧作等边△ABD和等边△BCE,连接AE、CD,二者交点为H。
求证:(1) AE=DC;
(2) ∠DHA=60°;
(3)连接GF,GF∥AC;
(4)连接HB,HB平分∠AHC。
【典例鉴赏】
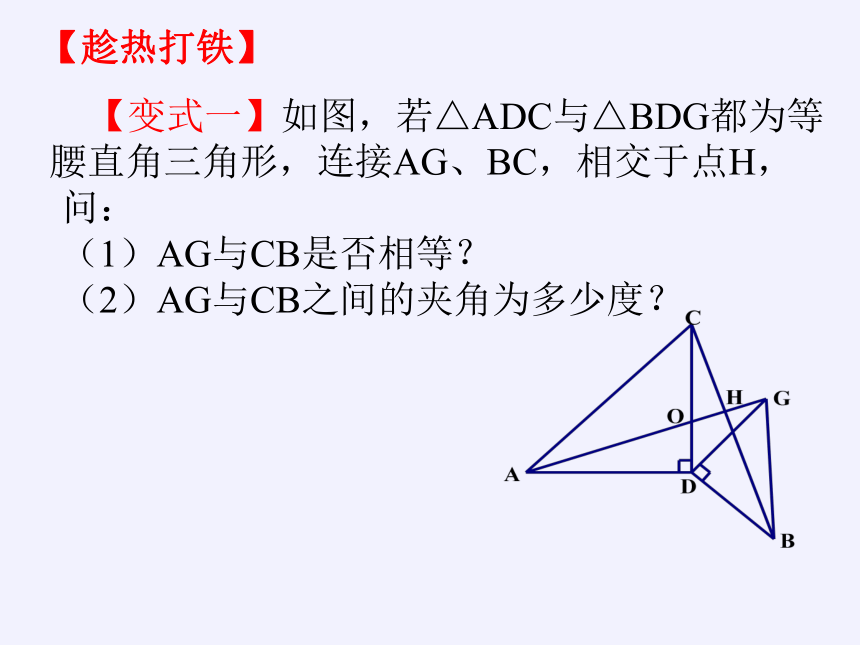
【变式一】如图,若△ADC与△BDG都为等腰直角三角形,连接AG、BC,相交于点H,
问:
(1)AG与CB是否相等?
(2)AG与CB之间的夹角为多少度?
【趁热打铁】
【变式二 】如图,两个正方形ABCD和DEFG,连接AG与CE,二者相交于H。问:
(1)△ADG≌△CDE是否成立?
(2)AG是否与CE相等?
(3)AG与CE之间的夹角为多少度?
(4)HD是否平分∠AHE?
旋转
A
B
C
D
E
模型1
A
B
C
D
E
D
E
顶角相等且顶点重合两个等腰三角形
全等三角形
手拉手模型----全等
口诀:“两等腰”共顶点;
“左左”“右右”手拉手;
借助全等易转换。
手拉手模型—全等三角形
△ABD≌△ACE
“A”型相似
【归纳】任意等腰三角形
导角核心:“8字型”
条件:△OAB,△OCD均为等腰三角形,且∠AOB = ∠COD
结论:
手拉手模型—相似三角形
D
E
B
C
A
一对对应角顶点重合的两个相似三角形
相似三角形
手拉手模型----相似三角形
口诀:相似三角共顶点;
“长长”“短短”连一连;
借助相似易转换。
模型2
“A”型相似(二)
例2 如图,△ACB∽△DCE, ,连接AD、BE,求 的值。
解:∵△ACB∽△DCE
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE
∵
∴ △ACD∽△BCE
∴ =k
∴∠ACB=∠DCE
(2018合肥市蜀山区二模)
△ACB∽△DCE
△ACD ∽△BCE
“手拉手”——相似
M
α
α
“手拉手”——全等
△ACB,△DCE为等腰三角形,∠ACB=∠DCE
△ACD ≌△BCE
α
α
C
A
B
E
D
M
知识总结
谢 谢!
α
α
C
A
B
E
D
M
M
α
α
(2018合肥四十五中一模)
(2)解:作FH⊥MN于H,
∵∠AEF=∠ABE=90°,∴∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,
∴∠FEH=∠BAE,
又∵AE=EF,
∠EHF=∠EBA=90°,∴△EFH≌△ABE,
∴FH=BE,EH=AB=BC, ∴CH=BE=FH,
∴ △CFH是等腰直角三角形
∴∠FCN=45°.
谢 谢
第22章 相似形(通用)
已知,如图,在△ABC中,以它的边AB,AC为边分别在形外作等边三角形△ABD,ACE,连接BE,DC,求证:BE=DC. (课本8上第150页12题)
【母题重现】
一、全等“手拉手”模型的特征:
两个顶角相等且有共顶点的等腰三角形组成的图形。(左手拉左手,右手拉右手)
2.“手”的判别:
判断左右:将等腰三角形顶角朝上,正对读者,读者左边为左手顶点,右边为右手顶点。
【火眼金睛】
例1 如图,在直线AB的同侧作等边△ABD和等边△BCE,连接AE、CD,二者交点为H。
求证:(1) AE=DC;
(2) ∠DHA=60°;
(3)连接GF,GF∥AC;
(4)连接HB,HB平分∠AHC。
【典例鉴赏】
【变式一】如图,若△ADC与△BDG都为等腰直角三角形,连接AG、BC,相交于点H,
问:
(1)AG与CB是否相等?
(2)AG与CB之间的夹角为多少度?
【趁热打铁】
【变式二 】如图,两个正方形ABCD和DEFG,连接AG与CE,二者相交于H。问:
(1)△ADG≌△CDE是否成立?
(2)AG是否与CE相等?
(3)AG与CE之间的夹角为多少度?
(4)HD是否平分∠AHE?
旋转
A
B
C
D
E
模型1
A
B
C
D
E
D
E
顶角相等且顶点重合两个等腰三角形
全等三角形
手拉手模型----全等
口诀:“两等腰”共顶点;
“左左”“右右”手拉手;
借助全等易转换。
手拉手模型—全等三角形
△ABD≌△ACE
“A”型相似
【归纳】任意等腰三角形
导角核心:“8字型”
条件:△OAB,△OCD均为等腰三角形,且∠AOB = ∠COD
结论:
手拉手模型—相似三角形
D
E
B
C
A
一对对应角顶点重合的两个相似三角形
相似三角形
手拉手模型----相似三角形
口诀:相似三角共顶点;
“长长”“短短”连一连;
借助相似易转换。
模型2
“A”型相似(二)
例2 如图,△ACB∽△DCE, ,连接AD、BE,求 的值。
解:∵△ACB∽△DCE
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE
∵
∴ △ACD∽△BCE
∴ =k
∴∠ACB=∠DCE
(2018合肥市蜀山区二模)
△ACB∽△DCE
△ACD ∽△BCE
“手拉手”——相似
M
α
α
“手拉手”——全等
△ACB,△DCE为等腰三角形,∠ACB=∠DCE
△ACD ≌△BCE
α
α
C
A
B
E
D
M
知识总结
谢 谢!
α
α
C
A
B
E
D
M
M
α
α
(2018合肥四十五中一模)
(2)解:作FH⊥MN于H,
∵∠AEF=∠ABE=90°,∴∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,
∴∠FEH=∠BAE,
又∵AE=EF,
∠EHF=∠EBA=90°,∴△EFH≌△ABE,
∴FH=BE,EH=AB=BC, ∴CH=BE=FH,
∴ △CFH是等腰直角三角形
∴∠FCN=45°.
谢 谢
