沪科版数学九年级上册 求几何面积问题 教案
文档属性
| 名称 | 沪科版数学九年级上册 求几何面积问题 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 113.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览

文档简介
二 次 函 数 解 决 问 题
—与面积有关(1)
【教材分析】
二次函数的应用本身是学习二次函数的图象与性质后,检验学生应用所学知识解决实际问题能力的一个综合考查。新课标中要求学生能通过对实际问题的情境的分析确定二次函数的表达式,体会其意义,能根据图象的性质解决简单的实际问题,而最值问题又是生活中利用二次函数知识解决最常见、最有实际应用价值的问题之一,它生活背景丰富,学生比较感兴趣,对于面积问题学生易于理解和接受,也为求解最大利润等问题奠定基础。目的在于让学生通过掌握求面积最大这一类题,学会用建模的思想去解决其它和函数有关的应用问题。
【学情及学法分析】
对九年级学生来说,在学习了一次函数和二次函数图象与性质以后,对函数的思想已有初步认识,对分析问题的方法已会初步模仿,能识别图象的增减性和最值,但在较为复杂的实际问题中,还不能熟练地应用知识解决问题。本节课正是为了弥补这一不足而设计的,目的是进一步培养学生利用所学知识构建数学模型,解决实际问题的能力,这也符合新课标中知识与技能呈螺旋式上升的规律。
【教学目标】
1.巩固二次函数y=(a≠0)的图象与性质,理解顶点与最值的关系,会求解最值问题。
2. 通过观察图象,理解顶点的特殊性,会把实际问题中的最值转化为二次函数的最值问题,通过动手动脑,提高分析解决问题的能力,并体会一般与特殊的关系,了解数形结合思想、函数思想。
3.通过学生之间的讨论、交流和探索,建立合作意识,提高探索能力,激发学习的兴趣和欲望,体会数学在生活中广泛的应用价值。
【教学重点】
利用二次函数求面积(围矩形)的最值问题。
【教学难点】
用含有x的代数式表示矩形的长和宽,正确构建数学模型解决面积问题。
【教学方法】
启发探究式、讨论交流式
【教学过程】
一. 创设问题情境,导入新课
1. 【引例】
总长为80厘米的铁丝围一个矩形,最大面积是 平方厘米。
(师生对话,引出课题并板书)
二.新课讲解
【温故知新】 已知抛物线 y= -x2+40x
1.开口方向:
2. 对称轴:
3. 顶点坐标:
4. 与x 轴的交点坐标 :
与y 轴的交点坐标 :
5. 当x 时,y随x的 增大而增大
当x 时,y随x的 增大而减小
6. 当x 时,函数有最 值,是
【解决引例】 师引导学生解决引例的问题,投影展示解题过程。
【问题变式】
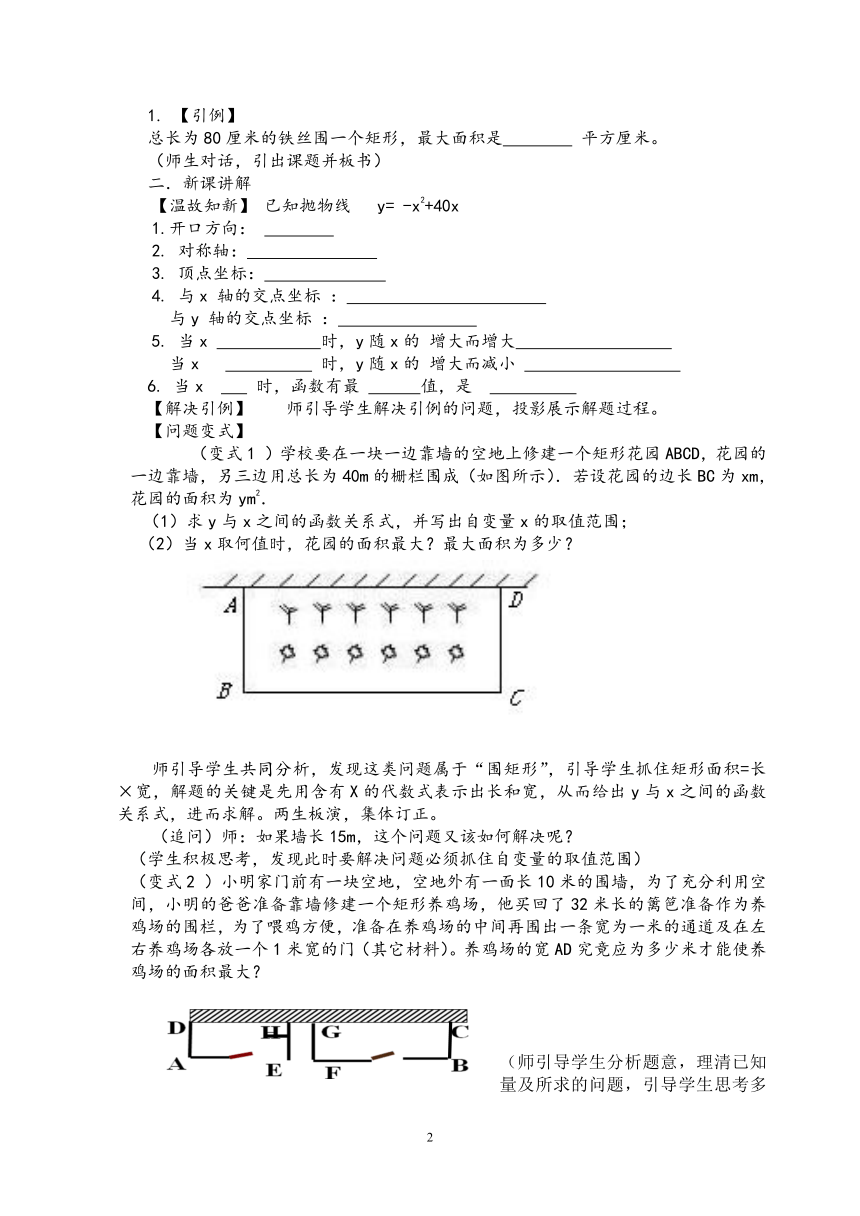
(变式1 )学校要在一块一边靠墙的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的边长BC为xm,花园的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x取何值时,花园的面积最大?最大面积为多少?
师引导学生共同分析,发现这类问题属于“围矩形”,引导学生抓住矩形面积=长×宽,解题的关键是先用含有X的代数式表示出长和宽,从而给出y与x之间的函数关系式,进而求解。两生板演,集体订正。
(追问)师:如果墙长15m,这个问题又该如何解决呢?
(学生积极思考,发现此时要解决问题必须抓住自变量的取值范围)
(变式2 )小明家门前有一块空地,空地外有一面长10米的围墙,为了充分利用空间,小明的爸爸准备靠墙修建一个矩形养鸡场,他买回了32米长的篱笆准备作为养鸡场的围栏,为了喂鸡方便,准备在养鸡场的中间再围出一条宽为一米的通道及在左右养鸡场各放一个1米宽的门(其它材料)。养鸡场的宽AD究竟应为多少米才能使养鸡场的面积最大?
(师引导学生分析题意,理清已知量及所求的问题,引导学生思考多种方法解决问题,培养学生的数学思维。对于AD的最终取值学生有争议,师给学生足够的时间和空间讨论交流,并引导学生结合草图进行分析,突破教学难点,从而解决问题。)
(变式3---链接中考)( 2015 安徽中考 第22题 )为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
(此题对学生提出了更高的要求,要求学生根据题意,抓住矩形区域ABCD的面积y可以有不同种求法,但是各种解题方法都必须抓住用含有x的代数式来表示各线段长,从而解决问题。)
三.课堂小结
1.如何用函数的知识来解决生活中面积最大类问题?
2.在解决问题的过程中应注意哪些问题?你学到了哪些思考问题的方法?
四.再思考
师:今天我们学习了用二次函数解决和面积有关的第一类问题,在后面的复习中我们将进一步解决和面积有关的其他问题,希望大家再接再励。(投影)
和面积有关(2)
1. 如图⑴,在Rt△ABC中,AC=3cm,BC=4cm,四边形CFDE为矩形,其中CF、CE在两直角边上,设矩形的一边CF=xcm.当x取何值时,矩形ECFD的面积最大?最大是多少?
2、如图⑵,在Rt△ABC中,作一个矩形DEGF,其中FG边在斜边上,AC=3cm,BC=4cm,那么矩形DEGF的面积最大是多少?
3、如图⑶,已知△ABC,矩形GDEF的DE边在BC边上.G、F分别在AB、AC边上,BC=5cm,S△ABC为30cm2,AH为△ABC在BC边上的高,求△ABC的内接矩形GDEF的最大面积.
和面积有关(3)
已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、
C(0,2)三点.
(1)求这条抛物线的解析式;
(2)如图一,点P是第一象限内此抛物线上的一个动点, 当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标。
五.送给学生的话
青青园中葵,朝露待日晞。
阳春布德泽,万物生光辉。
常恐秋节至,尡黄华叶衰。
百川东到海,何时复西归。
少壮不努力,老大徒伤悲。
PAGE
5
—与面积有关(1)
【教材分析】
二次函数的应用本身是学习二次函数的图象与性质后,检验学生应用所学知识解决实际问题能力的一个综合考查。新课标中要求学生能通过对实际问题的情境的分析确定二次函数的表达式,体会其意义,能根据图象的性质解决简单的实际问题,而最值问题又是生活中利用二次函数知识解决最常见、最有实际应用价值的问题之一,它生活背景丰富,学生比较感兴趣,对于面积问题学生易于理解和接受,也为求解最大利润等问题奠定基础。目的在于让学生通过掌握求面积最大这一类题,学会用建模的思想去解决其它和函数有关的应用问题。
【学情及学法分析】
对九年级学生来说,在学习了一次函数和二次函数图象与性质以后,对函数的思想已有初步认识,对分析问题的方法已会初步模仿,能识别图象的增减性和最值,但在较为复杂的实际问题中,还不能熟练地应用知识解决问题。本节课正是为了弥补这一不足而设计的,目的是进一步培养学生利用所学知识构建数学模型,解决实际问题的能力,这也符合新课标中知识与技能呈螺旋式上升的规律。
【教学目标】
1.巩固二次函数y=(a≠0)的图象与性质,理解顶点与最值的关系,会求解最值问题。
2. 通过观察图象,理解顶点的特殊性,会把实际问题中的最值转化为二次函数的最值问题,通过动手动脑,提高分析解决问题的能力,并体会一般与特殊的关系,了解数形结合思想、函数思想。
3.通过学生之间的讨论、交流和探索,建立合作意识,提高探索能力,激发学习的兴趣和欲望,体会数学在生活中广泛的应用价值。
【教学重点】
利用二次函数求面积(围矩形)的最值问题。
【教学难点】
用含有x的代数式表示矩形的长和宽,正确构建数学模型解决面积问题。
【教学方法】
启发探究式、讨论交流式
【教学过程】
一. 创设问题情境,导入新课
1. 【引例】
总长为80厘米的铁丝围一个矩形,最大面积是 平方厘米。
(师生对话,引出课题并板书)
二.新课讲解
【温故知新】 已知抛物线 y= -x2+40x
1.开口方向:
2. 对称轴:
3. 顶点坐标:
4. 与x 轴的交点坐标 :
与y 轴的交点坐标 :
5. 当x 时,y随x的 增大而增大
当x 时,y随x的 增大而减小
6. 当x 时,函数有最 值,是
【解决引例】 师引导学生解决引例的问题,投影展示解题过程。
【问题变式】
(变式1 )学校要在一块一边靠墙的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边用总长为40m的栅栏围成(如图所示).若设花园的边长BC为xm,花园的面积为ym2.
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x取何值时,花园的面积最大?最大面积为多少?
师引导学生共同分析,发现这类问题属于“围矩形”,引导学生抓住矩形面积=长×宽,解题的关键是先用含有X的代数式表示出长和宽,从而给出y与x之间的函数关系式,进而求解。两生板演,集体订正。
(追问)师:如果墙长15m,这个问题又该如何解决呢?
(学生积极思考,发现此时要解决问题必须抓住自变量的取值范围)
(变式2 )小明家门前有一块空地,空地外有一面长10米的围墙,为了充分利用空间,小明的爸爸准备靠墙修建一个矩形养鸡场,他买回了32米长的篱笆准备作为养鸡场的围栏,为了喂鸡方便,准备在养鸡场的中间再围出一条宽为一米的通道及在左右养鸡场各放一个1米宽的门(其它材料)。养鸡场的宽AD究竟应为多少米才能使养鸡场的面积最大?
(师引导学生分析题意,理清已知量及所求的问题,引导学生思考多种方法解决问题,培养学生的数学思维。对于AD的最终取值学生有争议,师给学生足够的时间和空间讨论交流,并引导学生结合草图进行分析,突破教学难点,从而解决问题。)
(变式3---链接中考)( 2015 安徽中考 第22题 )为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
(此题对学生提出了更高的要求,要求学生根据题意,抓住矩形区域ABCD的面积y可以有不同种求法,但是各种解题方法都必须抓住用含有x的代数式来表示各线段长,从而解决问题。)
三.课堂小结
1.如何用函数的知识来解决生活中面积最大类问题?
2.在解决问题的过程中应注意哪些问题?你学到了哪些思考问题的方法?
四.再思考
师:今天我们学习了用二次函数解决和面积有关的第一类问题,在后面的复习中我们将进一步解决和面积有关的其他问题,希望大家再接再励。(投影)
和面积有关(2)
1. 如图⑴,在Rt△ABC中,AC=3cm,BC=4cm,四边形CFDE为矩形,其中CF、CE在两直角边上,设矩形的一边CF=xcm.当x取何值时,矩形ECFD的面积最大?最大是多少?
2、如图⑵,在Rt△ABC中,作一个矩形DEGF,其中FG边在斜边上,AC=3cm,BC=4cm,那么矩形DEGF的面积最大是多少?
3、如图⑶,已知△ABC,矩形GDEF的DE边在BC边上.G、F分别在AB、AC边上,BC=5cm,S△ABC为30cm2,AH为△ABC在BC边上的高,求△ABC的内接矩形GDEF的最大面积.
和面积有关(3)
已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(2,0)、
C(0,2)三点.
(1)求这条抛物线的解析式;
(2)如图一,点P是第一象限内此抛物线上的一个动点, 当点P运动到什么位置时,四边形ABPC的面积最大?求出此时点P的坐标。
五.送给学生的话
青青园中葵,朝露待日晞。
阳春布德泽,万物生光辉。
常恐秋节至,尡黄华叶衰。
百川东到海,何时复西归。
少壮不努力,老大徒伤悲。
PAGE
5
