沪科版数学九年级上册 21.5 反比例函数图像和性质(课件)(共30张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 21.5 反比例函数图像和性质(课件)(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 00:00:00 | ||
图片预览





文档简介
(共30张PPT)
21.5 反比例函数的
图象及性质(2)
x
0
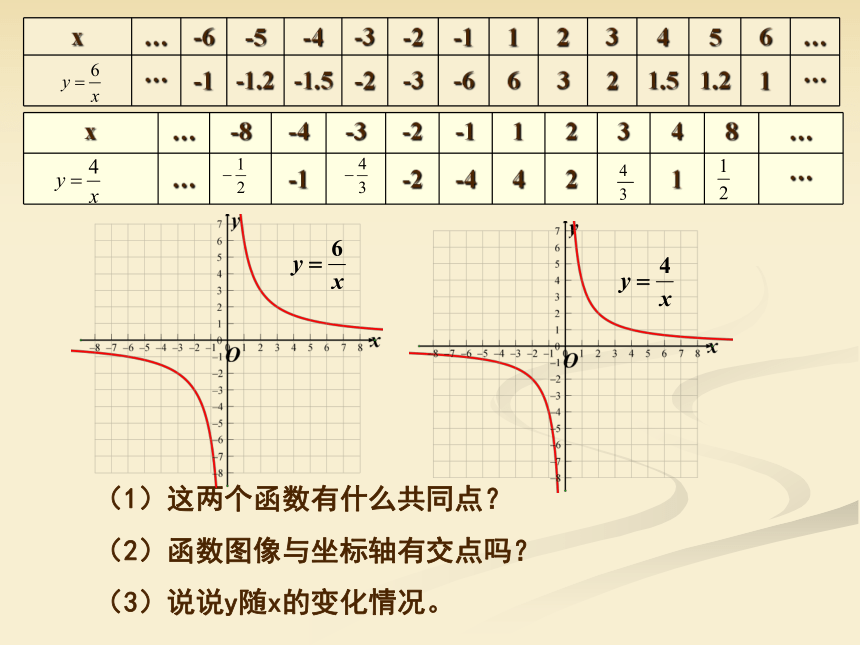
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -6 6 3 2 1.5 1.2 1 …
x … -8 -4 -3 -2 -1 1 2 3 4 8 …
… -1 -2 -4 4 2 1 …
(1)这两个函数有什么共同点?
(2)函数图像与坐标轴有交点吗?
(3)说说y随x的变化情况。
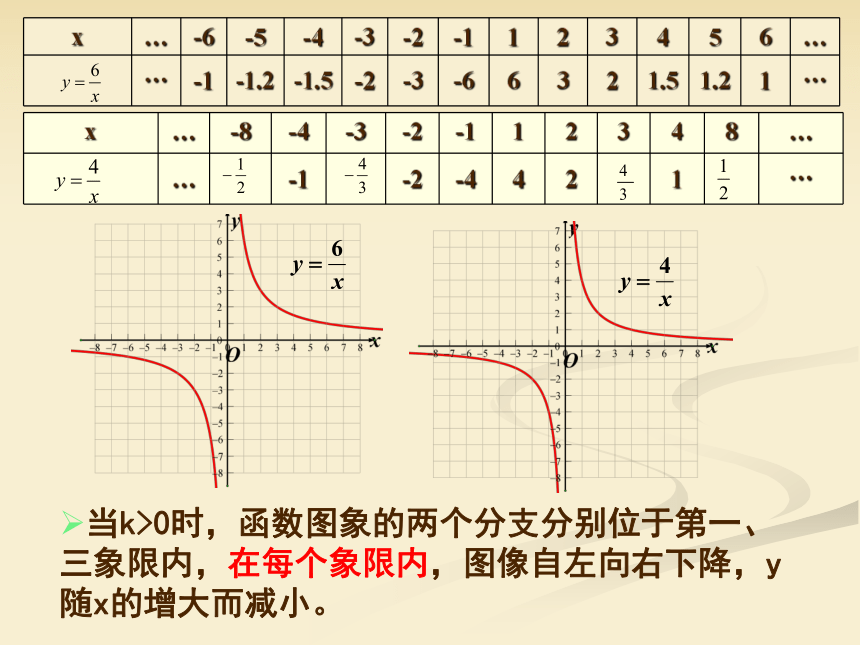
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -6 6 3 2 1.5 1.2 1 …
x … -8 -4 -3 -2 -1 1 2 3 4 8 …
… -1 -2 -4 4 2 1 …
当k>0时,函数图象的两个分支分别位于第一、三象限内,在每个象限内,图像自左向右下降,y随x的增大而减小。
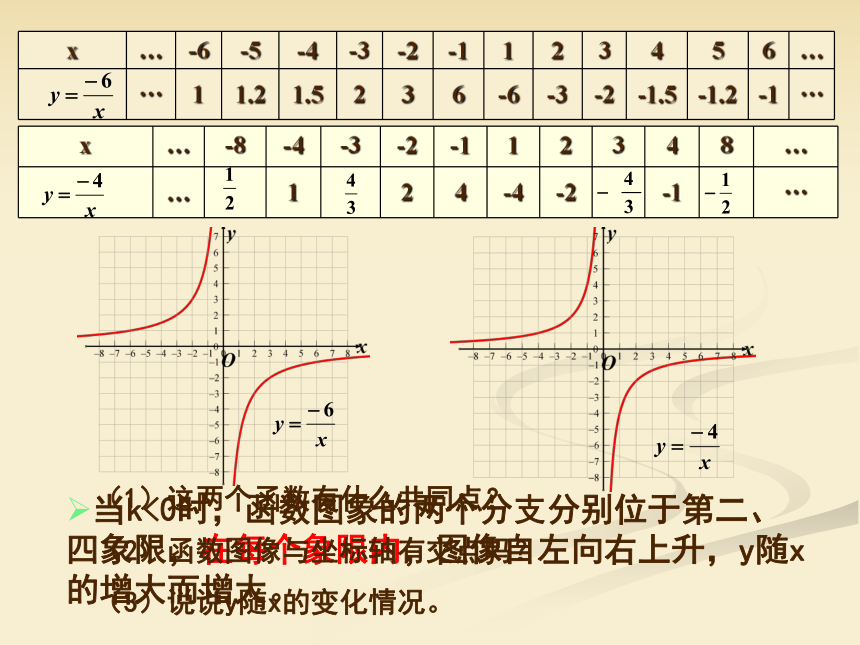
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… 1 1.2 1.5 2 3 6 -6 -3 -2 -1.5 -1.2 -1 …
x … -8 -4 -3 -2 -1 1 2 3 4 8 …
… 1 2 4 -4 -2 -1 …
当k<0时,函数图象的两个分支分别位于第二、四象限,在每个象限内,图像自左向右上升,y随x的增大而增大。
(1)这两个函数有什么共同点?
(2)函数图像与坐标轴有交点吗?
(3)说说y随x的变化情况。
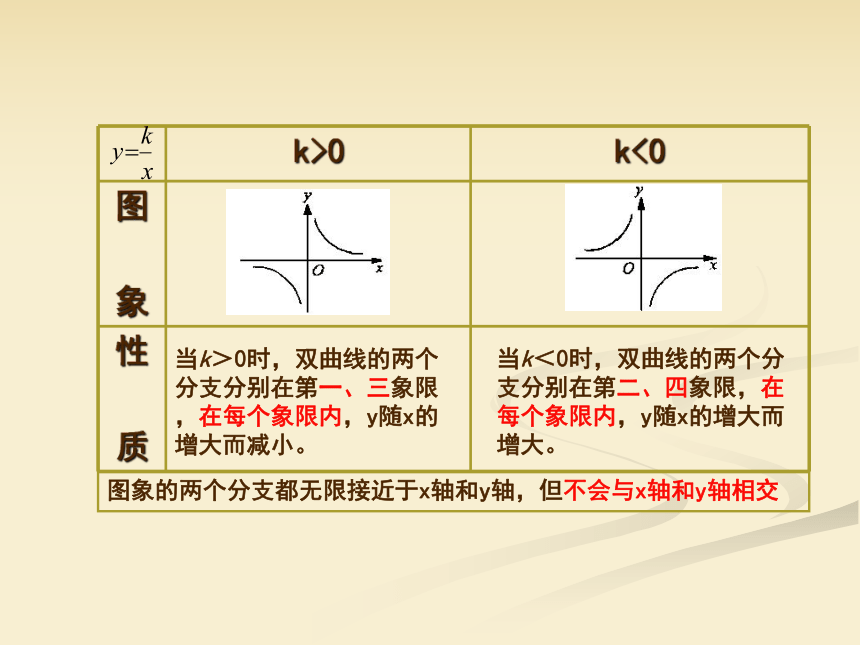
k>0 k<0
图
象
性
质
当k>0时,双曲线的两个分支分别在第一、三象限,在每个象限内,y随x的增大而减小。
当k<0时,双曲线的两个分支分别在第二、四象限,在每个象限内,y随x的增大而增大。
图象的两个分支都无限接近于x轴和y轴,但不会与x轴和y轴相交
小明把反比例函数 的图像画成了下面的样子,对吗?为什么?
如图,是反比例函数的图象的一个分支,对于给出的下列说法:
①常数k的取值范围是 ;
②另一个分支在第三象限;
③在函数图象上取点 和 ,
当 时, ;
④在函数图象的某一个分支上取点 和
,当 时, .
其中正确的是________________(在横线上填出正确
的序号).
①②④
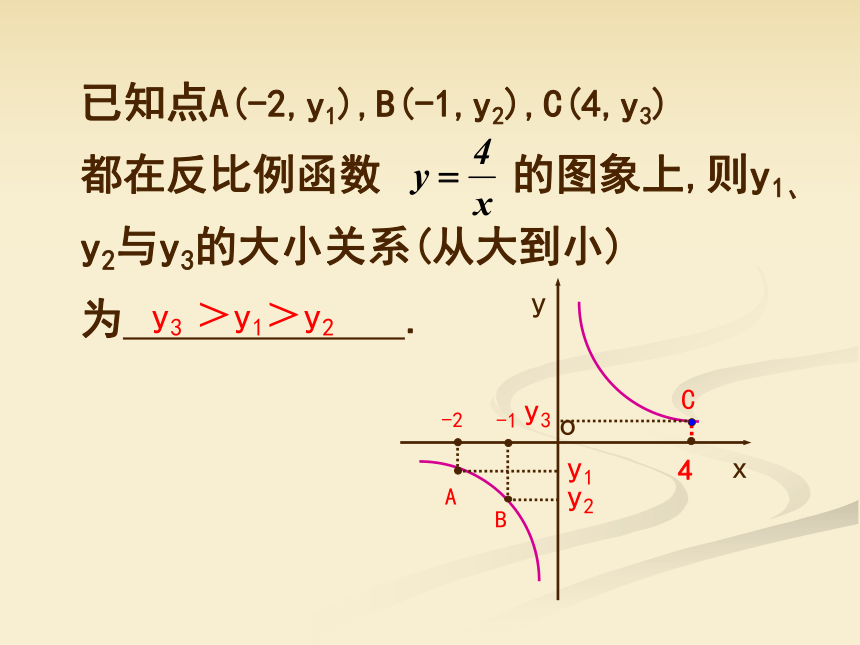
已知点A(-2,y1),B(-1,y2),C(4,y3)
都在反比例函数 的图象上,则y1、y2与y3的大小关系(从大到小)为 .
y
x
o
-1
y1
y2
A
B
-2
4
C
y3
y3 >y1>y2
在反比例函数 的图象上有三点(x1,y1)、(x2,y2)、(x3,y3),若x1>x2>0>x3,则y1,y2 与y3的大小为(从大到小) _____________
挑战自我
y3 >y1>y2
O
反比例函数图象的性质
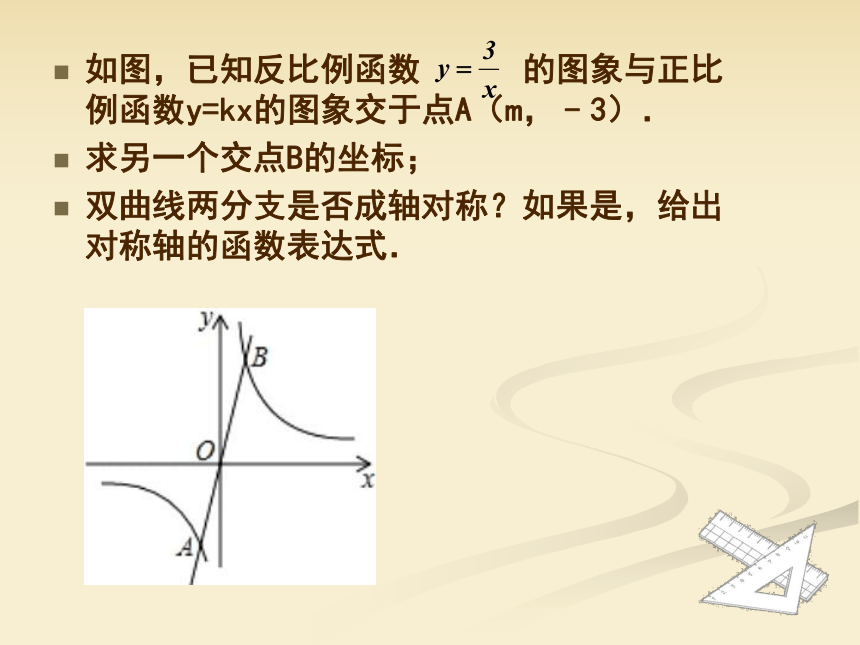
如图,已知反比例函数 的图象与正比例函数y=kx的图象交于点A(m,﹣3).
求另一个交点B的坐标;
双曲线两分支是否成轴对称?如果是,给出对称轴的函数表达式.
1、对反比例函数的认识
2、对解题方法的认识
k>0 k<0
图
象
性
质
当k>0时,双曲线的两个分支分别在第一、三象限,在每个象限内,y随x的增大而减小。
当k<0时,双曲线的两个分支分别在第二、四象限,在每个象限内,y随x的增大而增大。
图象的两个分支都无限接近于x轴和y轴,但不会与x轴和y轴相交
双曲线两个分支关于原点成中心对称
双曲线两分支关于y=x或y=-x成轴对称
解:1)当A、B在第一象限时,y1>y2。
2)当A、B在第三象限时, y1>y2,
3)当A在第三象限时、B在第一象限时, y1已知点A(x1,y1),B( x2,y2 )在反比例函数y= 的图象上,并且x1挑战自我
y
x
o
如图,已知反比例函数 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若M(x1,y1),N(x2,y2)
是反比例函数 图象上的
两点,且x1<x2,y1<y2,指出
点M、N各位于哪个象限,并简要
说明理由.
课后思考
再见
练习二:图像与性质
1、如图是三个反比例函数在x轴上方的图像, 由此观察得到( )
A k1>k2>k3 B k3>k2>k1
C k2>k1>k3 D k3>k1>k2
反比例函数图像两个分支关于原点成中心对称
反比例函数图象的性质
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
y =
x
6
… -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -2 -3 -6 6 3 2 1 …
第三象限
第一象限
-1.2
-1.5
1.5
1.2
… -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… 1 2 3 6 -6 -3 -2 -1 …
第二象限
第四象限
1.2
1.5
-1.5
-1.2
O
O
当k>0时,函数图象的两个分支分别位于第一、三象限内,在每个象限内,图像自左向右下降,y随x的增大而减小。
当k<0时,函数图象的两个分支分别位于第二、四象限内,在每个象限内,图像自左向右下降,y随x的增大而增大。
2.已知( ),( ),( )是反比例函数
的图象上的三个点,并且 ,则
的大小关系是( )
(A) (B)
(C) (D)
C
例1:如图是反比例函数 的图象一支,根据图象回答下列问题 :
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a,b)和B(a′,b′),如果a>a′,那么b和b′有怎样的大小关系?
解:(1)第三象限。
∵函数的图象在第一、第三象限
∴ m-5>0
解得 m>5
例1:如图是反比例函数 的图象一支,根据图象回答下列问题 :
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a,b)和B(a′,b′),如果a>a′,那么b和b′有怎样的大小关系?
解:(2)∵m-5>0,在每一象限内,y随x的增大而减小,
∴当a>a′时b<b′
O
O
函数图象的两个分支分别位于第一、三象限内,在每个象限内,图像自左向右下降,y随x的增大而减小。
函数图象的两个分支分别位于第二、四象限内,在每个象限内,图像自左向右上升,y随x的增大而增大。
反比例函数图象的性质
图象的两个分支都无限接近于x轴和y轴,但不会与x轴和y轴相交。
当k>0时,
当k<0时,
反比例函数图像两个分支关于原点成中心对称
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
y =
x
6
P(x0,y0)
P′(-x0,-y0)
反比例函数图象的性质
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -6 6 3 2 1.5 1.2 1 …
如图,是反比例函数的图象的一个分支,对于给出的下列说法:
① 另一个分支在第三象限;
② 在函数图象上取点 和 ,
当 时, ;
③ 在函数图象的某一个分支上取点 和
,当 时, .
④在函数图象的某一个分支上取点 和
,当 时, .
其中正确的是________________(在横线上填出正确
的序号).
①④
综合运用:
21.5 反比例函数的
图象及性质(2)
x
0
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -6 6 3 2 1.5 1.2 1 …
x … -8 -4 -3 -2 -1 1 2 3 4 8 …
… -1 -2 -4 4 2 1 …
(1)这两个函数有什么共同点?
(2)函数图像与坐标轴有交点吗?
(3)说说y随x的变化情况。
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -6 6 3 2 1.5 1.2 1 …
x … -8 -4 -3 -2 -1 1 2 3 4 8 …
… -1 -2 -4 4 2 1 …
当k>0时,函数图象的两个分支分别位于第一、三象限内,在每个象限内,图像自左向右下降,y随x的增大而减小。
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… 1 1.2 1.5 2 3 6 -6 -3 -2 -1.5 -1.2 -1 …
x … -8 -4 -3 -2 -1 1 2 3 4 8 …
… 1 2 4 -4 -2 -1 …
当k<0时,函数图象的两个分支分别位于第二、四象限,在每个象限内,图像自左向右上升,y随x的增大而增大。
(1)这两个函数有什么共同点?
(2)函数图像与坐标轴有交点吗?
(3)说说y随x的变化情况。
k>0 k<0
图
象
性
质
当k>0时,双曲线的两个分支分别在第一、三象限,在每个象限内,y随x的增大而减小。
当k<0时,双曲线的两个分支分别在第二、四象限,在每个象限内,y随x的增大而增大。
图象的两个分支都无限接近于x轴和y轴,但不会与x轴和y轴相交
小明把反比例函数 的图像画成了下面的样子,对吗?为什么?
如图,是反比例函数的图象的一个分支,对于给出的下列说法:
①常数k的取值范围是 ;
②另一个分支在第三象限;
③在函数图象上取点 和 ,
当 时, ;
④在函数图象的某一个分支上取点 和
,当 时, .
其中正确的是________________(在横线上填出正确
的序号).
①②④
已知点A(-2,y1),B(-1,y2),C(4,y3)
都在反比例函数 的图象上,则y1、y2与y3的大小关系(从大到小)为 .
y
x
o
-1
y1
y2
A
B
-2
4
C
y3
y3 >y1>y2
在反比例函数 的图象上有三点(x1,y1)、(x2,y2)、(x3,y3),若x1>x2>0>x3,则y1,y2 与y3的大小为(从大到小) _____________
挑战自我
y3 >y1>y2
O
反比例函数图象的性质
如图,已知反比例函数 的图象与正比例函数y=kx的图象交于点A(m,﹣3).
求另一个交点B的坐标;
双曲线两分支是否成轴对称?如果是,给出对称轴的函数表达式.
1、对反比例函数的认识
2、对解题方法的认识
k>0 k<0
图
象
性
质
当k>0时,双曲线的两个分支分别在第一、三象限,在每个象限内,y随x的增大而减小。
当k<0时,双曲线的两个分支分别在第二、四象限,在每个象限内,y随x的增大而增大。
图象的两个分支都无限接近于x轴和y轴,但不会与x轴和y轴相交
双曲线两个分支关于原点成中心对称
双曲线两分支关于y=x或y=-x成轴对称
解:1)当A、B在第一象限时,y1>y2。
2)当A、B在第三象限时, y1>y2,
3)当A在第三象限时、B在第一象限时, y1
y
x
o
如图,已知反比例函数 与一次函数y=k2x+b的图象交于点A(1,8)、B(﹣4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)若M(x1,y1),N(x2,y2)
是反比例函数 图象上的
两点,且x1<x2,y1<y2,指出
点M、N各位于哪个象限,并简要
说明理由.
课后思考
再见
练习二:图像与性质
1、如图是三个反比例函数在x轴上方的图像, 由此观察得到( )
A k1>k2>k3 B k3>k2>k1
C k2>k1>k3 D k3>k1>k2
反比例函数图像两个分支关于原点成中心对称
反比例函数图象的性质
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
y =
x
6
… -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -2 -3 -6 6 3 2 1 …
第三象限
第一象限
-1.2
-1.5
1.5
1.2
… -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… 1 2 3 6 -6 -3 -2 -1 …
第二象限
第四象限
1.2
1.5
-1.5
-1.2
O
O
当k>0时,函数图象的两个分支分别位于第一、三象限内,在每个象限内,图像自左向右下降,y随x的增大而减小。
当k<0时,函数图象的两个分支分别位于第二、四象限内,在每个象限内,图像自左向右下降,y随x的增大而增大。
2.已知( ),( ),( )是反比例函数
的图象上的三个点,并且 ,则
的大小关系是( )
(A) (B)
(C) (D)
C
例1:如图是反比例函数 的图象一支,根据图象回答下列问题 :
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a,b)和B(a′,b′),如果a>a′,那么b和b′有怎样的大小关系?
解:(1)第三象限。
∵函数的图象在第一、第三象限
∴ m-5>0
解得 m>5
例1:如图是反比例函数 的图象一支,根据图象回答下列问题 :
(1)图象的另一支在哪个象限?常数m的取值范围是什么?
(2)在这个函数图象的某一支上任取点A(a,b)和B(a′,b′),如果a>a′,那么b和b′有怎样的大小关系?
解:(2)∵m-5>0,在每一象限内,y随x的增大而减小,
∴当a>a′时b<b′
O
O
函数图象的两个分支分别位于第一、三象限内,在每个象限内,图像自左向右下降,y随x的增大而减小。
函数图象的两个分支分别位于第二、四象限内,在每个象限内,图像自左向右上升,y随x的增大而增大。
反比例函数图象的性质
图象的两个分支都无限接近于x轴和y轴,但不会与x轴和y轴相交。
当k>0时,
当k<0时,
反比例函数图像两个分支关于原点成中心对称
1
2
3
4
5
6
-1
-3
-2
-4
-5
-6
1
2
3
4
-1
-2
-3
-4
0
-6
-5
5
6
y
y =
x
6
P(x0,y0)
P′(-x0,-y0)
反比例函数图象的性质
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -6 6 3 2 1.5 1.2 1 …
如图,是反比例函数的图象的一个分支,对于给出的下列说法:
① 另一个分支在第三象限;
② 在函数图象上取点 和 ,
当 时, ;
③ 在函数图象的某一个分支上取点 和
,当 时, .
④在函数图象的某一个分支上取点 和
,当 时, .
其中正确的是________________(在横线上填出正确
的序号).
①④
综合运用:
