《互斥事件》课件
图片预览







文档简介
课件25张PPT。欢迎来到数学课堂!试验的所有结果只有有限个
且每次只有一个结果.
(2)每一个试验结果出现的可能性相同.1.古典概型的特征2.古典概型概率公式温故知新渐入佳境1. 鱼与熊掌不可兼得;3. 考试中的单项选择题。4. 掷骰子,向上的点数分别是
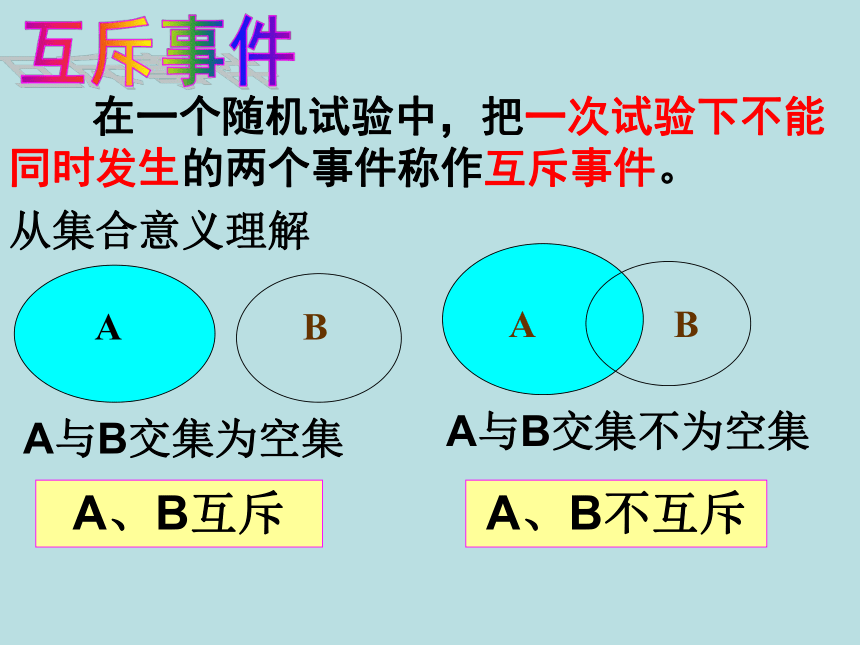
1、2、3、4、5、6.共同点:不能同时发生!2. 抽奖时,“中奖”和“不中奖” 。北师大版数学必修3第三章 概率2.3 互斥事件(一)A、B互斥A、B不互斥从集合意义理解 在一个随机试验中,把一次试验下不能同时发生的两个事件称作互斥事件。互斥事件 例1 抛掷一枚骰子一次,下面的事件A与事件B是互斥事件吗?(1) 事件A=“点数为2”, B=“点数为3”;
(2) A=“点数为偶数”, B=“点数为5”;
(3) A=“点数不超过3”, B=“点数超过3”;
(4) A=“点数为6”, B=“点数超过4”.解 互斥事件: (1)(2)(3)小试牛刀 给定事件A,B,规定A+B为一个事件,叫做A、B的和事件。事件A+B发生是指(1) “A发生B不发生”;
(2) “A不发生B发生”;
(3) “A、B同时发生”. 事件A=“点数为2”,事件B=“点数为3”,
记事件“点数为2或3”为A+B.事件A和事件B至少有一个发生.和事件(2)事件A=“点数为偶数”,事件B=“点数为5”;
(3)事件A=“点数不超过3”,事件B=“点数超过3”;
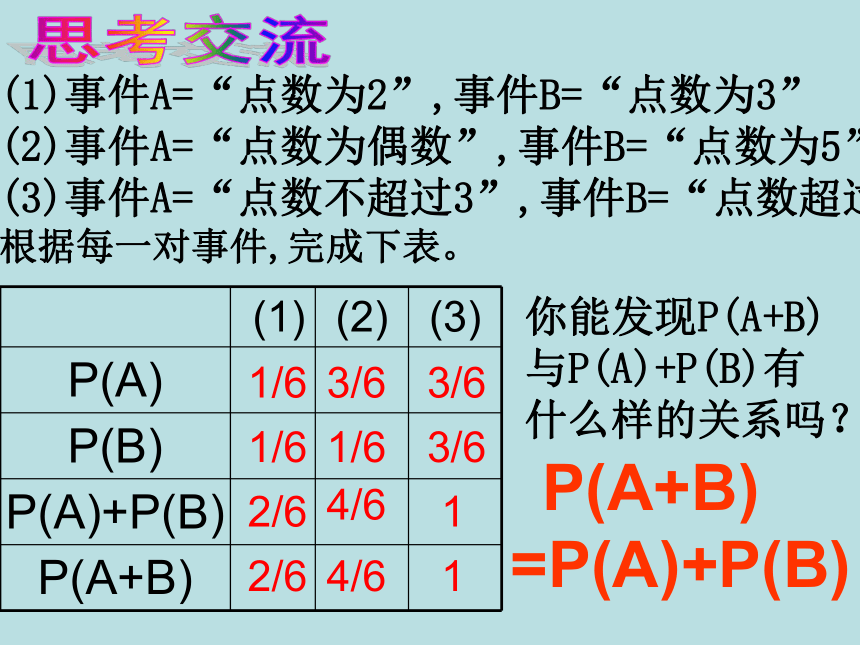
(4)事件A=“点数为6”,事件B=“点数超过4”. 对于例1(2)(3)(4)中的事件A和B,A+B各表示什么事件?趁热打铁(1)事件A=“点数为2”,事件B=“点数为3”
(2)事件A=“点数为偶数”,事件B=“点数为5”
(3)事件A=“点数不超过3”,事件B=“点数超过3”
根据每一对事件,完成下表。你能发现P(A+B)
与P(A)+P(B)有
什么样的关系吗? P(A+B)
=P(A)+P(B)思考交流 对于(4)A=“点数为6”,事件B=“点数超过4”,P(A+B)=P(A)+P(B)还成立吗? NO! P(A+B)=P(A)+P(B)
(A、B为互斥事件.)概率加法公式提炼精华 P(A1+A2+…+An)
=P(A1)+P(A2)+…+P(An)提炼精华 例2 从一箱新产品中随机地抽取一件新产品,设A=“抽到的是一等品”,
B=“抽到的是二等品”,
C=“抽到的是三等品”,
且P(A)=0.7, P(B)=0.1,P(C)=0.05.
求下列事件的概率.
(1)事件D=“抽到的是一等品或三等品”;
(2)事件E=“抽到的是二等品或三等品”.
(3)事件D+E表示什么?P(D+E)=P(D)+P(E)吗?大显身手 例1中(3)事件A=“点数不超过3”,事件
B=“点数超过3”有P(A+B)=P(A)+P(B)=1.(1)概率和为1,事件A+B是必然
事件,即A和B中必有一个发生;
(2)A、B为互斥事件.对立事件对立事件一定是互斥事件;
互斥事件未必是对立事件.对立事件 不能同时发生且必有一个发生的两个事件叫做互为对立事件。思考:互斥事件与对立事件有何关系?实践出真知教材143页练习1,2.⑴求他参加不超过2个小组的概率;
⑵求他至少参加了2个小组的概率. 例3 某学校成立了数学、英语、音乐3个课外兴趣小组,分别有39,32,33个成员,一些成员参加了不止1个小组,具体情况如图.随机选取1个成员:大显身手解(1)设A=“选取的成员参加不超过2个小组”,A1=“选取成员只参加1个小组”,A2=“选取成员只参加2个小组”,则A1与A2为互斥事件。⑴求他参加不超过
2个小组的概率;你还有别的方法吗? 当事件A比较复杂时,可通过A的
对立事件求A,兴许会简单点.善于总结(2)求他至少参加了2个小组的概率;实践出真知教材143页练习3,4. 判断下列事件是不是互斥事件,如果是,
再判断它们是不是对立事件,如果不是,分别
说出它们的对立事件.一次抽取三件产品,
(1)“恰有一件是次品”与“恰有两件次品”;
(2)“至少有一件次品”与“全是次品”;
(3)“至少有一件正品”与“至少有一件次品”;
(4)“至少有一件次品”与“全是正品”.精雕细琢1.互斥事件:不可能同时发生的两个事件叫做互斥事件。若事件A与B互斥,则P(A+B)=P(A)+P(B).当A、B是对立事件时,P(B)=1-P(A).2.对立事件:必有一个发生的两个互斥事件
叫做对立事件。3.二者的关系:颗粒归仓若事件A1,A2,…,An彼此互斥,则P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).对立事件一定是互斥事件;
互斥事件未必是对立事件.思考与作业作业 课本第148页第9,10题.争分夺秒1. 对飞机连续射击两次,每次发射一枚炮弹,
记事件A:两次都击中飞机.
事件B:两次都没有击中飞机.
事件C:恰有一次击中飞机.
事件D:至少有一次击中飞机.
其中互斥事件是 .A与B,A与C,B与C,B与D.2. 经统计,在某储蓄所一个营业窗口等候的人数为及相应概率如下:(1) 至少3人排队等候的概率是多少?
(2) 有人排队等候的概率是多少?争分夺秒谢谢观看!
且每次只有一个结果.
(2)每一个试验结果出现的可能性相同.1.古典概型的特征2.古典概型概率公式温故知新渐入佳境1. 鱼与熊掌不可兼得;3. 考试中的单项选择题。4. 掷骰子,向上的点数分别是
1、2、3、4、5、6.共同点:不能同时发生!2. 抽奖时,“中奖”和“不中奖” 。北师大版数学必修3第三章 概率2.3 互斥事件(一)A、B互斥A、B不互斥从集合意义理解 在一个随机试验中,把一次试验下不能同时发生的两个事件称作互斥事件。互斥事件 例1 抛掷一枚骰子一次,下面的事件A与事件B是互斥事件吗?(1) 事件A=“点数为2”, B=“点数为3”;
(2) A=“点数为偶数”, B=“点数为5”;
(3) A=“点数不超过3”, B=“点数超过3”;
(4) A=“点数为6”, B=“点数超过4”.解 互斥事件: (1)(2)(3)小试牛刀 给定事件A,B,规定A+B为一个事件,叫做A、B的和事件。事件A+B发生是指(1) “A发生B不发生”;
(2) “A不发生B发生”;
(3) “A、B同时发生”. 事件A=“点数为2”,事件B=“点数为3”,
记事件“点数为2或3”为A+B.事件A和事件B至少有一个发生.和事件(2)事件A=“点数为偶数”,事件B=“点数为5”;
(3)事件A=“点数不超过3”,事件B=“点数超过3”;
(4)事件A=“点数为6”,事件B=“点数超过4”. 对于例1(2)(3)(4)中的事件A和B,A+B各表示什么事件?趁热打铁(1)事件A=“点数为2”,事件B=“点数为3”
(2)事件A=“点数为偶数”,事件B=“点数为5”
(3)事件A=“点数不超过3”,事件B=“点数超过3”
根据每一对事件,完成下表。你能发现P(A+B)
与P(A)+P(B)有
什么样的关系吗? P(A+B)
=P(A)+P(B)思考交流 对于(4)A=“点数为6”,事件B=“点数超过4”,P(A+B)=P(A)+P(B)还成立吗? NO! P(A+B)=P(A)+P(B)
(A、B为互斥事件.)概率加法公式提炼精华 P(A1+A2+…+An)
=P(A1)+P(A2)+…+P(An)提炼精华 例2 从一箱新产品中随机地抽取一件新产品,设A=“抽到的是一等品”,
B=“抽到的是二等品”,
C=“抽到的是三等品”,
且P(A)=0.7, P(B)=0.1,P(C)=0.05.
求下列事件的概率.
(1)事件D=“抽到的是一等品或三等品”;
(2)事件E=“抽到的是二等品或三等品”.
(3)事件D+E表示什么?P(D+E)=P(D)+P(E)吗?大显身手 例1中(3)事件A=“点数不超过3”,事件
B=“点数超过3”有P(A+B)=P(A)+P(B)=1.(1)概率和为1,事件A+B是必然
事件,即A和B中必有一个发生;
(2)A、B为互斥事件.对立事件对立事件一定是互斥事件;
互斥事件未必是对立事件.对立事件 不能同时发生且必有一个发生的两个事件叫做互为对立事件。思考:互斥事件与对立事件有何关系?实践出真知教材143页练习1,2.⑴求他参加不超过2个小组的概率;
⑵求他至少参加了2个小组的概率. 例3 某学校成立了数学、英语、音乐3个课外兴趣小组,分别有39,32,33个成员,一些成员参加了不止1个小组,具体情况如图.随机选取1个成员:大显身手解(1)设A=“选取的成员参加不超过2个小组”,A1=“选取成员只参加1个小组”,A2=“选取成员只参加2个小组”,则A1与A2为互斥事件。⑴求他参加不超过
2个小组的概率;你还有别的方法吗? 当事件A比较复杂时,可通过A的
对立事件求A,兴许会简单点.善于总结(2)求他至少参加了2个小组的概率;实践出真知教材143页练习3,4. 判断下列事件是不是互斥事件,如果是,
再判断它们是不是对立事件,如果不是,分别
说出它们的对立事件.一次抽取三件产品,
(1)“恰有一件是次品”与“恰有两件次品”;
(2)“至少有一件次品”与“全是次品”;
(3)“至少有一件正品”与“至少有一件次品”;
(4)“至少有一件次品”与“全是正品”.精雕细琢1.互斥事件:不可能同时发生的两个事件叫做互斥事件。若事件A与B互斥,则P(A+B)=P(A)+P(B).当A、B是对立事件时,P(B)=1-P(A).2.对立事件:必有一个发生的两个互斥事件
叫做对立事件。3.二者的关系:颗粒归仓若事件A1,A2,…,An彼此互斥,则P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).对立事件一定是互斥事件;
互斥事件未必是对立事件.思考与作业作业 课本第148页第9,10题.争分夺秒1. 对飞机连续射击两次,每次发射一枚炮弹,
记事件A:两次都击中飞机.
事件B:两次都没有击中飞机.
事件C:恰有一次击中飞机.
事件D:至少有一次击中飞机.
其中互斥事件是 .A与B,A与C,B与C,B与D.2. 经统计,在某储蓄所一个营业窗口等候的人数为及相应概率如下:(1) 至少3人排队等候的概率是多少?
(2) 有人排队等候的概率是多少?争分夺秒谢谢观看!
