《余弦函数图像与性质》课件
图片预览







文档简介
课件24张PPT。余弦函数的图象与性质正弦函数的图象
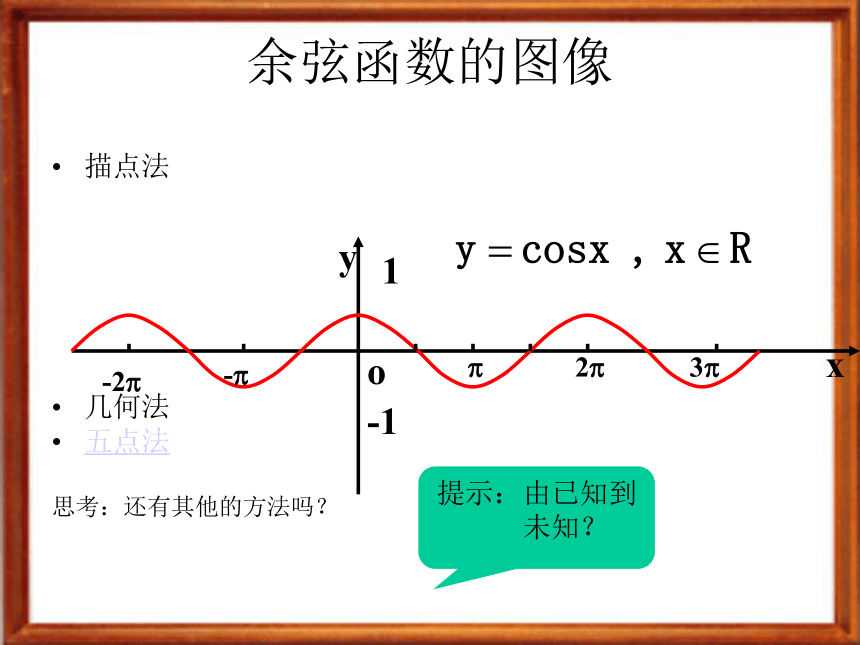
描点法
几何法
五点法(关键点)思考: 余弦函数怎么画呢?余弦函数的图像描点法
几何法
五点法
思考:还有其他的方法吗?
提示:由已知到未知?作余弦函数 y=cosx (x∈R) 的图象 思考:如何将余弦函数用诱导公式写成正弦函数? 注:余弦曲线的图象可以通过将正弦曲线向左平移 个单位长度而得到。余弦函数的图象叫做余弦曲线。 正弦、余弦函数的图象 余弦函数的图象 正弦函数的图象 y=cosx=sin(x+ ), x?R余弦曲线(0,1)( ,0)( ? ,-1)( ,0)( 2? ,1)正弦曲线形状完全一样只是位置不同我们已经学习了正弦函数的性质,能不能类比学习余弦函数的性质呢?
定义域
值域
周期性
单调性
奇偶性
对称性
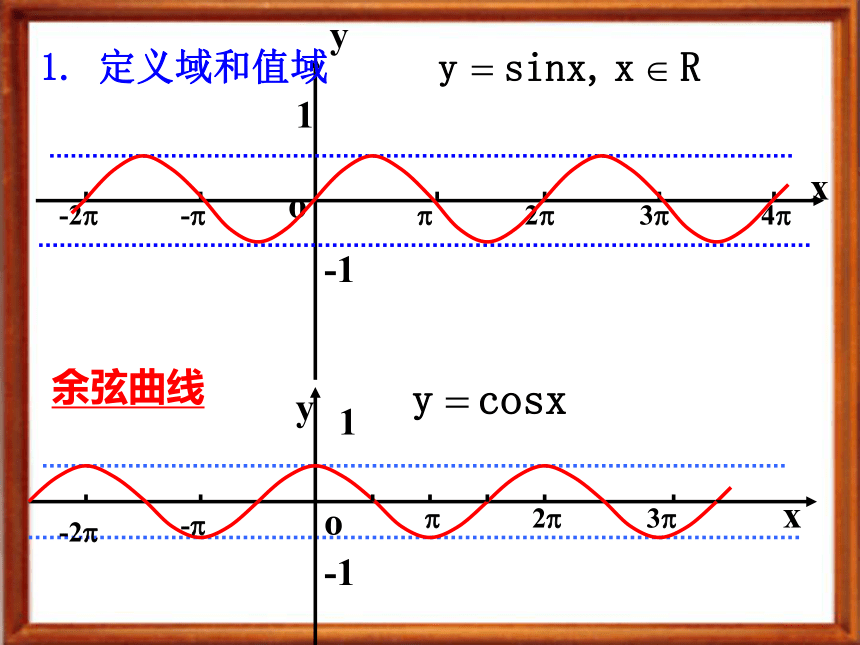
具体有哪些不同呢?余弦函数的性质xyo1-1-2?-??2?3?4?1. 定义域和值域
RR y=sinx (x R) 当x= 时,函数值y取得最大值1;当x= 时,函数值y取得最小值-1 y=cosx (x R) 当x= 时,函数值y取得最大值1;当x= 时,函数值y取得最小值-1观察下面图象:因为终边相同的角的三角函数值相同,所以y=sinx的图象在……,
…与y=sinx,x∈[0,2π]的图象相同正弦曲线的周期2. 周期性因为终边相同的角的三角函数值相同,所以y=cosx的图象在……,
…与y=cosx,x∈[0,2π]的图象相同余弦曲线的周期 由此可知,都是这两个函数的周期。是它的周期,最小正周期为 3.正弦、余弦函数的奇偶性sin(-x)= - sinx (x?R) y=sinx (x?R)是奇函数 正弦函数的奇偶性图像关于原点对称 3. 正弦、余弦函数的奇偶性cos(-x)= cosx (x?R) y=cosx (x?R)是偶函数 正弦、余弦函数的奇偶性 一般的,对于函数f(x)的定义域内的任意一个x,都有f(-x) = f(x),则称f(x)为这一定义域内的偶函数。关于y轴对称 3.正弦、余弦函数的奇偶性sin(-x)= - sinx (x?R) y=sinx (x?R)是奇函数cos(-x)= cosx (x?R) y=cosx (x?R)是偶函数定义域关于原点对称 正弦、余弦函数的奇偶性 4.正弦、余弦函数的单调性 正弦函数的单调性 y=sinx (x?R)增区间为 [ , ] 其值从-1增至1 … 0 … … ? …-1 0 1 0 -1减区间为 [ , ] 其值从 1减至-1[ +2k?, +2k?],k?Z[ +2k?, +2k?],k?Z 4.正弦、余弦函数的单调性 余弦函数的单调性 y=cosx (x?R) -? … … 0 … … ?-1 0 1 0 -1 增区间为 其值从-1到1 减区间为 其值从-1到15. 对称性 y=sinx (x R) 观察下面图象: y=cosx (x R) 观察下面图象:x∈ Rx∈ R[-1,1][-1,1]x= 2kπ时 ymax=1
x= 2kπ+ π时 ymin=-1
周期为T=2π周期为T=2π奇函数 偶函数在x∈[2kπ- π , 2kπ ]
上都是增函数 。
在x∈[2kπ, 2kπ+ π ]
上都是减函数 , (kπ,0)
x = kπ例子 例 画出函数y= cosx-1,x?[0, 2?]的简图,并讨论性质: 0 ? 2 ?10-101 0 -1 -2 -1 0 y= cosx-1,x?[0, 2?]y=cosx,x?[0, 2?]还有其他方法吗 余弦函数的图象 小
结1.余弦曲线五点法
2.注意与正弦函数的性质对比来理解余弦函数的性质正弦函数得出(借助诱导公式)
谢谢!
作业:课本P33 2、4
描点法
几何法
五点法(关键点)思考: 余弦函数怎么画呢?余弦函数的图像描点法
几何法
五点法
思考:还有其他的方法吗?
提示:由已知到未知?作余弦函数 y=cosx (x∈R) 的图象 思考:如何将余弦函数用诱导公式写成正弦函数? 注:余弦曲线的图象可以通过将正弦曲线向左平移 个单位长度而得到。余弦函数的图象叫做余弦曲线。 正弦、余弦函数的图象 余弦函数的图象 正弦函数的图象 y=cosx=sin(x+ ), x?R余弦曲线(0,1)( ,0)( ? ,-1)( ,0)( 2? ,1)正弦曲线形状完全一样只是位置不同我们已经学习了正弦函数的性质,能不能类比学习余弦函数的性质呢?
定义域
值域
周期性
单调性
奇偶性
对称性
具体有哪些不同呢?余弦函数的性质xyo1-1-2?-??2?3?4?1. 定义域和值域
RR y=sinx (x R) 当x= 时,函数值y取得最大值1;当x= 时,函数值y取得最小值-1 y=cosx (x R) 当x= 时,函数值y取得最大值1;当x= 时,函数值y取得最小值-1观察下面图象:因为终边相同的角的三角函数值相同,所以y=sinx的图象在……,
…与y=sinx,x∈[0,2π]的图象相同正弦曲线的周期2. 周期性因为终边相同的角的三角函数值相同,所以y=cosx的图象在……,
…与y=cosx,x∈[0,2π]的图象相同余弦曲线的周期 由此可知,都是这两个函数的周期。是它的周期,最小正周期为 3.正弦、余弦函数的奇偶性sin(-x)= - sinx (x?R) y=sinx (x?R)是奇函数 正弦函数的奇偶性图像关于原点对称 3. 正弦、余弦函数的奇偶性cos(-x)= cosx (x?R) y=cosx (x?R)是偶函数 正弦、余弦函数的奇偶性 一般的,对于函数f(x)的定义域内的任意一个x,都有f(-x) = f(x),则称f(x)为这一定义域内的偶函数。关于y轴对称 3.正弦、余弦函数的奇偶性sin(-x)= - sinx (x?R) y=sinx (x?R)是奇函数cos(-x)= cosx (x?R) y=cosx (x?R)是偶函数定义域关于原点对称 正弦、余弦函数的奇偶性 4.正弦、余弦函数的单调性 正弦函数的单调性 y=sinx (x?R)增区间为 [ , ] 其值从-1增至1 … 0 … … ? …-1 0 1 0 -1减区间为 [ , ] 其值从 1减至-1[ +2k?, +2k?],k?Z[ +2k?, +2k?],k?Z 4.正弦、余弦函数的单调性 余弦函数的单调性 y=cosx (x?R) -? … … 0 … … ?-1 0 1 0 -1 增区间为 其值从-1到1 减区间为 其值从-1到15. 对称性 y=sinx (x R) 观察下面图象: y=cosx (x R) 观察下面图象:x∈ Rx∈ R[-1,1][-1,1]x= 2kπ时 ymax=1
x= 2kπ+ π时 ymin=-1
周期为T=2π周期为T=2π奇函数 偶函数在x∈[2kπ- π , 2kπ ]
上都是增函数 。
在x∈[2kπ, 2kπ+ π ]
上都是减函数 , (kπ,0)
x = kπ例子 例 画出函数y= cosx-1,x?[0, 2?]的简图,并讨论性质: 0 ? 2 ?10-101 0 -1 -2 -1 0 y= cosx-1,x?[0, 2?]y=cosx,x?[0, 2?]还有其他方法吗 余弦函数的图象 小
结1.余弦曲线五点法
2.注意与正弦函数的性质对比来理解余弦函数的性质正弦函数得出(借助诱导公式)
谢谢!
作业:课本P33 2、4
