《椭圆》课件
图片预览





文档简介
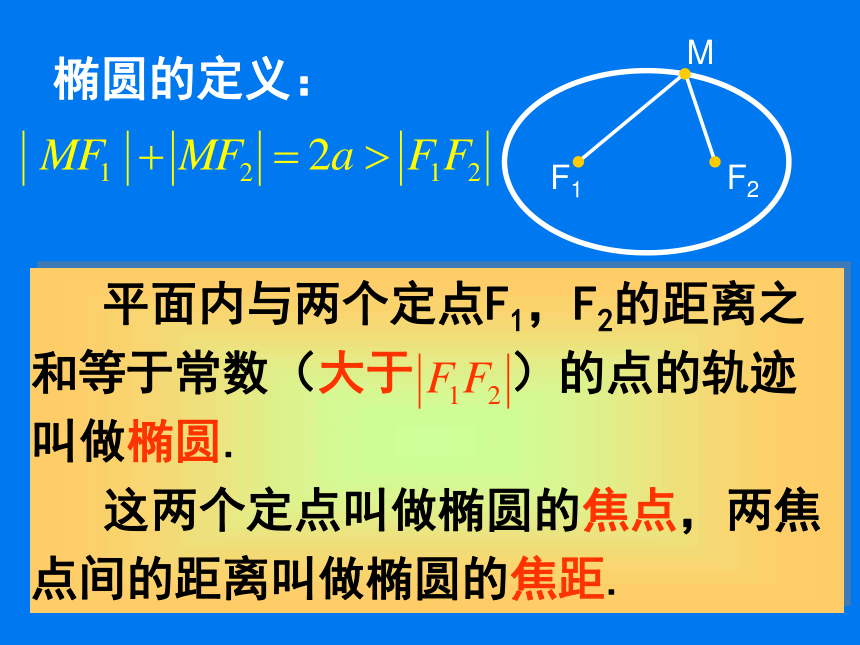
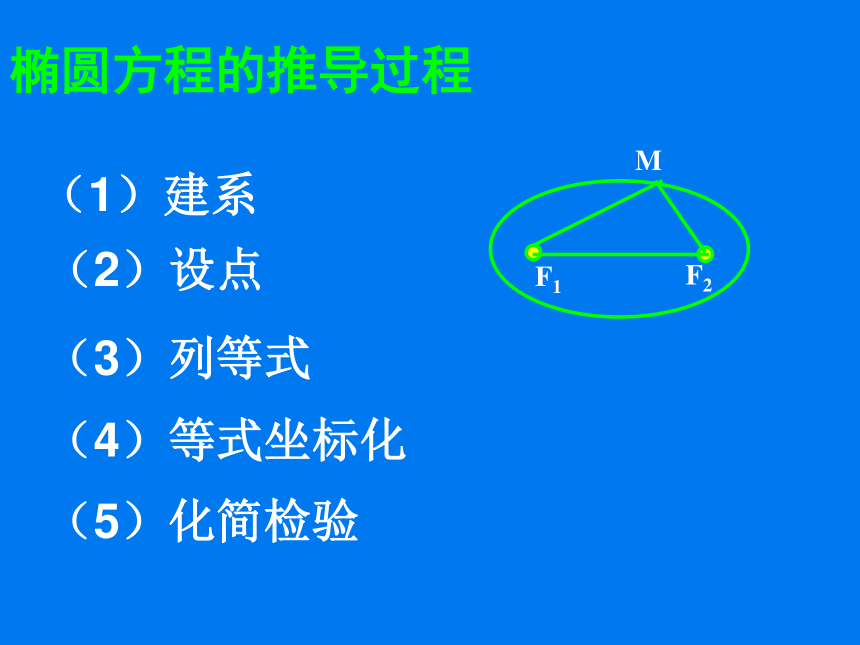
课件21张PPT。椭圆的标准方程及定义开普勒行星运动定律所有行星绕太阳运行的轨道都是______,太阳处在_______________.椭圆?思考:椭圆定义 的副本.gsp椭圆的定义:动点M的轨迹:线段F1F2 . F1 F2 动点M的轨迹:不存在. 思考:用定义判断下列动点M的轨迹是否为椭圆.(1)到F1(-5,0)、F2(5,0)的距离之和为12的点的轨迹.(2)到F1(0,-5)、F2(0,5)的距离之和为4的点的轨迹.是不是椭圆方程的推导过程F1F2M(1)建系
(2)设点
(3)列等式 (4)等式坐标化
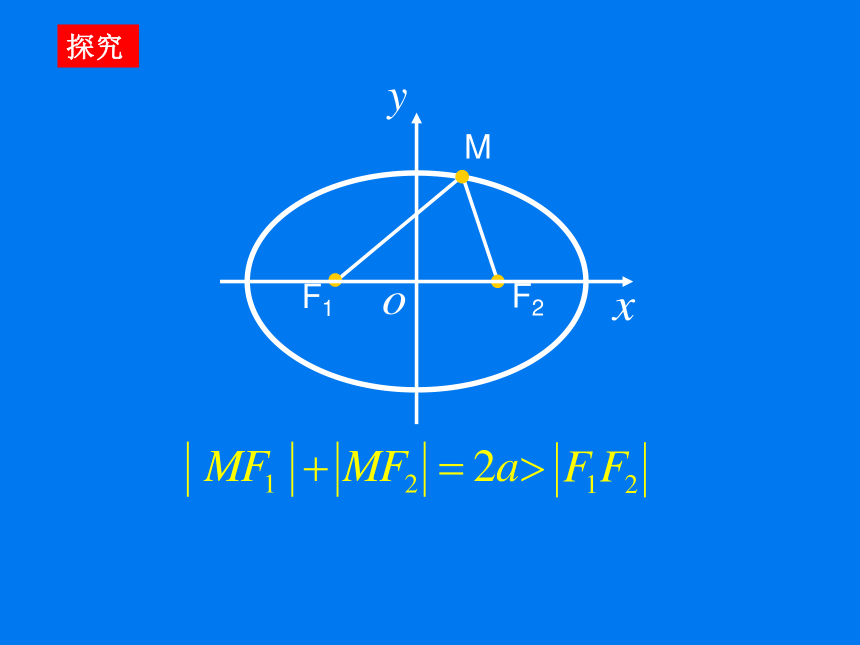
(5)化简检验MF1 F2 探究解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .(问题:下面怎样化简?)由椭圆的定义得,限制条件:代入坐标移项,再平方
两边再平方,得整理得:MF1 F2 Pc a b 探究椭圆方程中a,b,c的几何意义:椭圆的标准方程结论:总体印象:对称、简洁,“像”直线方程的截距式焦点在y轴:焦点在x轴:思考椭圆的标准方程的两种类型椭圆的标准方程当焦点在x轴上时:当焦点在y轴上时:结论得出:注意:焦点所在位置要看谁的分母大答:在 x 轴上(-3,0)和(3,0)答:在 y 轴上(0,-5)和(0,5)答:在y 轴上(0,-1)和(0,1)判定下列椭圆的焦点在 哪个轴上,并指明a2、b2,写出焦点坐标.练习:例1 写出适合下列条件的椭圆的标准
方程.(1)a = 4 , b = 1, 焦点在x轴上.例题:例2 已知椭圆两个焦点的坐标分别
是(0,-2),(0,2),并且经过点(2,3),求它的标准方程.求椭圆标准方程的方法和步骤:(1)根据焦点所在位置设出标准方程 (3)写出椭圆的方程.结论:(2)根据已知条件求出a,b(1)椭圆的定义:(2)标准方程的两种形式:(3)求椭圆方程.课堂小结:作业:
(2)设点
(3)列等式 (4)等式坐标化
(5)化简检验MF1 F2 探究解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a (2a>2c) ,则F1、F2的坐标分别是(?c,0)、(c,0) .(问题:下面怎样化简?)由椭圆的定义得,限制条件:代入坐标移项,再平方
两边再平方,得整理得:MF1 F2 Pc a b 探究椭圆方程中a,b,c的几何意义:椭圆的标准方程结论:总体印象:对称、简洁,“像”直线方程的截距式焦点在y轴:焦点在x轴:思考椭圆的标准方程的两种类型椭圆的标准方程当焦点在x轴上时:当焦点在y轴上时:结论得出:注意:焦点所在位置要看谁的分母大答:在 x 轴上(-3,0)和(3,0)答:在 y 轴上(0,-5)和(0,5)答:在y 轴上(0,-1)和(0,1)判定下列椭圆的焦点在 哪个轴上,并指明a2、b2,写出焦点坐标.练习:例1 写出适合下列条件的椭圆的标准
方程.(1)a = 4 , b = 1, 焦点在x轴上.例题:例2 已知椭圆两个焦点的坐标分别
是(0,-2),(0,2),并且经过点(2,3),求它的标准方程.求椭圆标准方程的方法和步骤:(1)根据焦点所在位置设出标准方程 (3)写出椭圆的方程.结论:(2)根据已知条件求出a,b(1)椭圆的定义:(2)标准方程的两种形式:(3)求椭圆方程.课堂小结:作业:
