2021-2022学年山东省聊城市东昌府区部分学校联考九年级(上)月考数学试卷(12月份)(Word版 含解析)
文档属性
| 名称 | 2021-2022学年山东省聊城市东昌府区部分学校联考九年级(上)月考数学试卷(12月份)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 07:43:14 | ||
图片预览



文档简介
2021-2022学年山东省聊城市东昌府区部分学校联考九年级第一学期月考数学试卷(12月份)
一、选择题(每小题3分,共12小题,满分36分)
1.在△ABC中,∠C=90°,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
2.关于x的一元二次方程ax2﹣5x+a2+a=0的一个根是0,则a的值是( )
A.0 B.1 C.﹣1 D.0或﹣1
3.如图,点P在△ABC的边AC上,下列条件中不能判断△ABP∽△ACB的是( )
A.∠ABP=∠C B.∠APB=∠ABC C.= D.=
4.用配方法解一元二次方程x2﹣4x﹣5=0的过程中,配方正确的是( )
A.(x+2)2=1 B.(x﹣2)2=1 C.(x+2)2=9 D.(x﹣2)2=9
5.在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
6.某县为发展教育事业,加强了对教育经费的投入,2012年投入3000万元,预计2014年投入5000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )
A.3000x2=5000
B.3000(1+x)2=5000
C.3000(1+x%)2=5000
D.3000(1+x)+3000(1+x)2=5000
7.如图,四边形ABCD为⊙O的内接四边形,E是BC延长线上的一点,已知∠BOD=130°,则∠DCE的度数为( )
A.45° B.50° C.65° D.75°
8.在函数y=中,自变量x的取值范围是( )
A.x≥﹣2且x≠1 B.x≤2且x≠1 C.x≠1 D.x≤﹣2
9.⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )
A.4 B.6 C.6 D.8
10.小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为16米,坡面上的影长为8米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
A.12+2米 B.24米 C.8+4米 D.20米
11.下列叙述正确的有( )
①圆内接四边形对角相等;②圆的切线垂直于圆的半径;③正多边形中心角的度数等于这个正多边形一个外角的度数;④过圆外一点所画的圆的两条切线长相等;⑤边长为6的正三角形,其边心距为2.
A.1个 B.2个 C.3个 D.4个
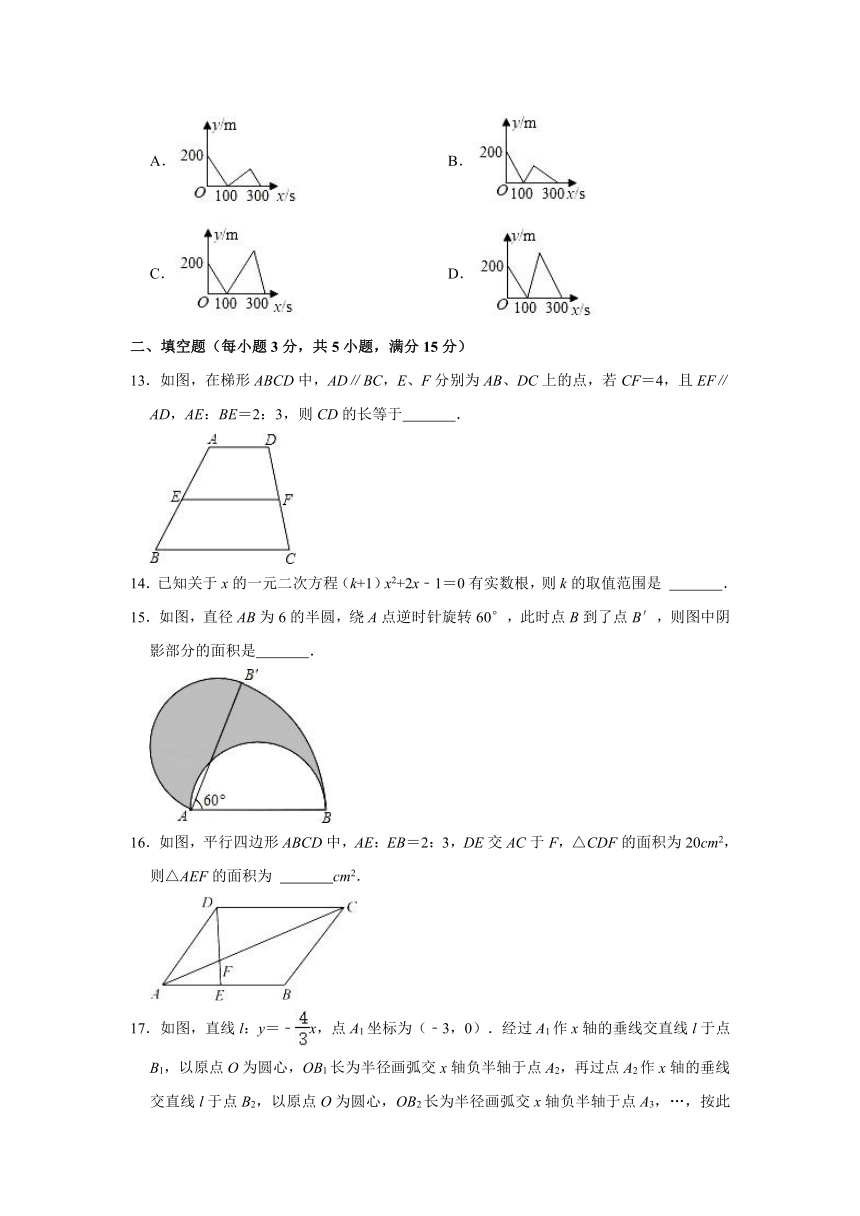
12.甲、乙两名同学在一段2000m长的笔直公路上进行自行车比赛,开始时甲在起点,乙在甲的前方200m处,他们同时同向出发匀速前进,甲的速度是8m/s,乙的速度是6m/s,先到达终点者在终点处等待.设甲、乙两人之间的距离是y(m),比赛时间是x(s),整个过程中y与x之间的函数关系的图象大致是( )
A. B.
C. D.
二、填空题(每小题3分,共5小题,满分15分)
13.如图,在梯形ABCD中,AD∥BC,E、F分别为AB、DC上的点,若CF=4,且EF∥AD,AE:BE=2:3,则CD的长等于 .
14.已知关于x的一元二次方程(k+1)x2+2x﹣1=0有实数根,则k的取值范围是 .
15.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 .
16.如图,平行四边形ABCD中,AE:EB=2:3,DE交AC于F,△CDF的面积为20cm2,则△AEF的面积为 cm2.
17.如图,直线l:y=﹣x,点A1坐标为(﹣3,0).经过A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2021的坐标为 .
三、解答题(共8小题,满分69分)
18.(1)解方程3x2+2x﹣2=0;
(2)解方程3x(x﹣1)=x﹣1;
(3)计算2cos60°+4sin60° tan30°﹣6cos245°.
19.如图,某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?
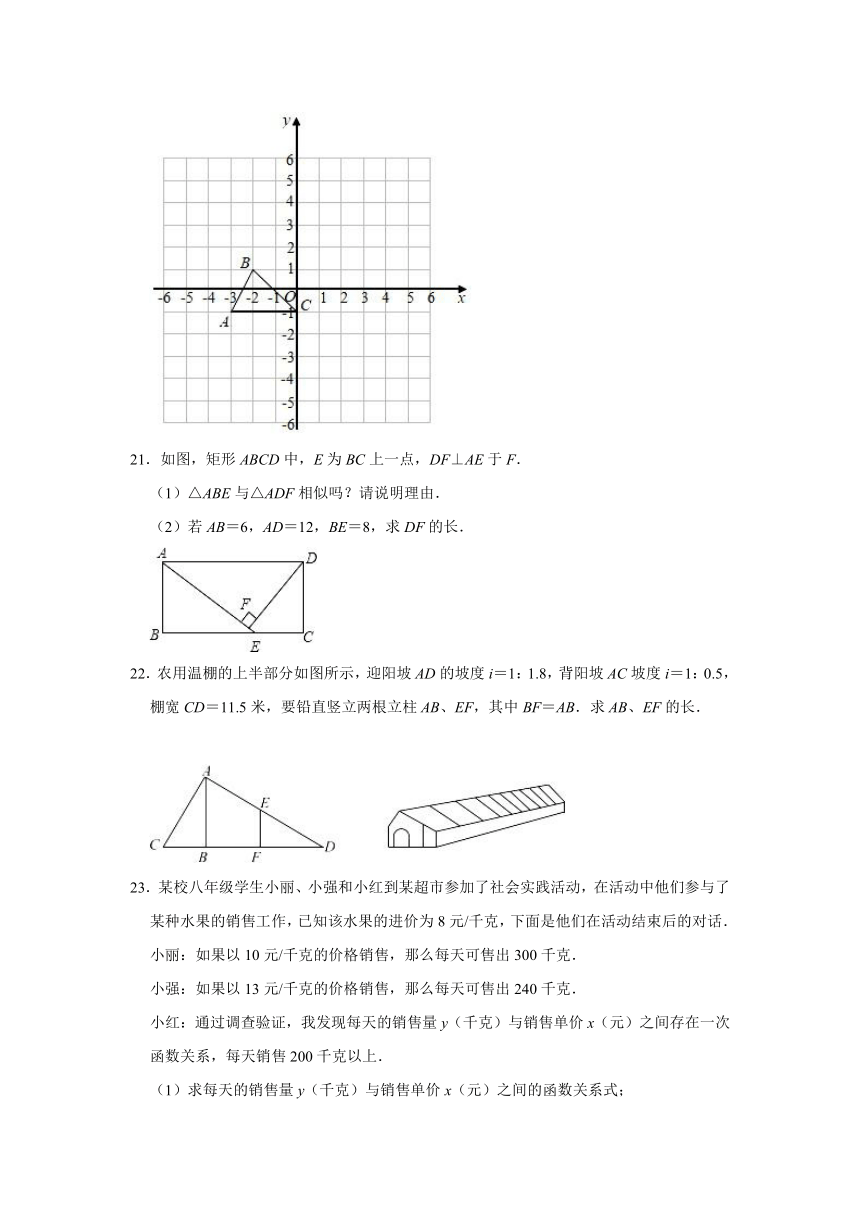
20.如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的相似比为1:2,画出△A1B1C1,并标出△A1B1C1外接圆的圆心P,直接写出P点的坐标.
(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1,B1,C1)
(2)作出△ABC绕点C逆时针旋转90°后的图形△A2B2C,并求出点B经过的路径长.(结果保留根号和π)
21.如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
22.农用温棚的上半部分如图所示,迎阳坡AD的坡度i=1:1.8,背阳坡AC坡度i=1:0.5,棚宽CD=11.5米,要铅直竖立两根立柱AB、EF,其中BF=AB.求AB、EF的长.
23.某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可售出240千克.
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系,每天销售200千克以上.
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式;
(2)该超市销售这种水果每天获取的利润达到1040元,那么销售单价为多少元?
24.如图,AE=AF,以AE为直径作⊙O交EF点D,过点D作BC⊥AF,交AE的延长线于点B.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=5,AC=4,求BE的长.
25.已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动,速度为1cm/;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动时间为xs(0<x<2),解答下列问题:
(1)如图①,当x为何值时,△APQ与△ACB相似;
(2)如图②,连接PC,当x为何值时,PQ=PC;
(3)是否存在某时刻x,使线段PQ恰好把Rt△ACB面积平分?若存在,求出此时x的值;若不存在,说明理由.
参考答案
一、选择题(每小题3分,共12小题,满分36分)
1.在△ABC中,∠C=90°,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
【分析】先根据BC=2,sinA=求出AB的长度,再利用勾股定理即可求解.
解:∵sinA==,BC=2,
∴AB=3.
∴AC===.
故选:A.
2.关于x的一元二次方程ax2﹣5x+a2+a=0的一个根是0,则a的值是( )
A.0 B.1 C.﹣1 D.0或﹣1
【分析】根据一元二次方程的解的定义得到a2+a=0,解得a1=0,a2=﹣1,然后根据一元二次方程的定义确定满足条件的a的值.
解:把x=0代入ax2﹣5x+a2+a=0得a2+a=0,解得a1=0,a2=﹣1,
而a≠0,
所以a=﹣1.
故选:C.
3.如图,点P在△ABC的边AC上,下列条件中不能判断△ABP∽△ACB的是( )
A.∠ABP=∠C B.∠APB=∠ABC C.= D.=
【分析】根据相似三角形的判定定理(①有两角分别相等的两三角形相似,②有两边的比相等,并且它们的夹角也相等的两三角形相似)逐个进行判断即可.
解:A、∵∠A=∠A,∠ABP=∠C,
∴△ABP∽△ACB,故本选项错误;
B、∵∠A=∠A,∠APB=∠ABC,
∴△ABP∽△ACB,故本选项错误;
C、∵∠A=∠A,=,
∴△ABP∽△ACB.
故故本选项错误.
D、正确.不能判定△ABP∽△ACB.
故选:D.
4.用配方法解一元二次方程x2﹣4x﹣5=0的过程中,配方正确的是( )
A.(x+2)2=1 B.(x﹣2)2=1 C.(x+2)2=9 D.(x﹣2)2=9
【分析】先移项,再方程两边都加上一次项系数一半的平方,即可得出答案.
解:移项得:x2﹣4x=5,
配方得:x2﹣4x+22=5+22,
(x﹣2)2=9,
故选:D.
5.在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
【分析】首先画出图形,根据点的坐标得到圆心到X轴的距离是4,到Y轴的距离是3,根据直线与圆的位置关系即可求出答案.
解:圆心到X轴的距离是4,到y轴的距离是3,
4=4,3<4,
∴圆与x轴相切,与y轴相交,
故选:C.
6.某县为发展教育事业,加强了对教育经费的投入,2012年投入3000万元,预计2014年投入5000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )
A.3000x2=5000
B.3000(1+x)2=5000
C.3000(1+x%)2=5000
D.3000(1+x)+3000(1+x)2=5000
【分析】增长率问题,一般用增长后的量=增长前的量×(1+增长率),参照本题,如果设教育经费的年平均增长率为x,根据“2012年投入3000万元,预计2014年投入5000万元”,可以分别用x表示2012以后两年的投入,然后根据已知条件可得出方程.
解:设教育经费的年平均增长率为x,
则2013的教育经费为:3000×(1+x)万元,
2014的教育经费为:3000×(1+x)2万元,
那么可得方程:3000×(1+x)2=5000.
故选:B.
7.如图,四边形ABCD为⊙O的内接四边形,E是BC延长线上的一点,已知∠BOD=130°,则∠DCE的度数为( )
A.45° B.50° C.65° D.75°
【分析】根据圆周角定理求出∠A,根据圆内接四边形的性质得出∠DCE=∠A,代入求出即可.
解:∵∠BOD=130°,
∴∠A=∠BOD=65°,
∵四边形ABCD为⊙O的内接四边形,
∴∠DCE=∠A=65°,
故选:C.
8.在函数y=中,自变量x的取值范围是( )
A.x≥﹣2且x≠1 B.x≤2且x≠1 C.x≠1 D.x≤﹣2
【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.
解:由题意得,x+2≥0且x﹣1≠0,
解得x≥﹣2且x≠1.
故选:A.
9.⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )
A.4 B.6 C.6 D.8
【分析】过O作OC⊥AB于C,连接OA,根据含30°角的直角三角形的性质得出OC=MO=3,根据勾股定理求出AC,再根据垂径定理得出AB=2AC,最后求出答案即可.
解:过O作OC⊥AB于C,连接OA,则∠OCA=90°,
∵MO=6,∠OMA=30°,
∴OC=MO=3,
在Rt△OCA中,由勾股定理得:AC===4,
∵OC⊥AB,OC过O,
∴BC=AC,
即AB=2AC=2×4=8,
故选:D.
10.小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为16米,坡面上的影长为8米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
A.12+2米 B.24米 C.8+4米 D.20米
【分析】延长AC交BF延长线于D点,则BD即为AB的影长,然后根据物长和影长的比值计算即可.
解:延长AC交BF延长线于D点,
则∠CFE=30°,作CE⊥BD于E,
在Rt△CFE中,∠CFE=30°,CF=8m,
∴CE=4(米),EF=8cos30°=4(米),
在Rt△CED中,
∵同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,CE=4(米),CE:DE=1:2,
∴DE=8(米),
∴BD=BF+EF+ED=16+4+8=24+4(米)
在Rt△ABD中,AB=BD=(24+4)=(12+2)(米),
故选:A.
11.下列叙述正确的有( )
①圆内接四边形对角相等;②圆的切线垂直于圆的半径;③正多边形中心角的度数等于这个正多边形一个外角的度数;④过圆外一点所画的圆的两条切线长相等;⑤边长为6的正三角形,其边心距为2.
A.1个 B.2个 C.3个 D.4个
【分析】利用圆内接四边形的性质、圆周角定理分别判断后即可确定正确的选项个数.
解:①圆内接四边形对角互补,故①不符合题意;
②圆的切线垂直于过切点的半径,故②不符合题意;
③正n多边形中心角的度数等于,这个正多边形的外角和为360°,一个外角的度数等于,故③符合题意;
④过圆外一点所画的圆的两条切线长相等,正确,故④符合题意;
⑤如图,△ABC为正三角形,点O为其中心;
OD⊥BC于点D;连接OB、OC;
∵OA=OC,∠BOC=×360°=120°,
∴BD=BC=3,∠BOD=120°=60°,
∴tan∠BOD=,
∴OD=×6×=,
即边长为6的正三角形的边心距为,故⑤不符合题意,
故选:B.
12.甲、乙两名同学在一段2000m长的笔直公路上进行自行车比赛,开始时甲在起点,乙在甲的前方200m处,他们同时同向出发匀速前进,甲的速度是8m/s,乙的速度是6m/s,先到达终点者在终点处等待.设甲、乙两人之间的距离是y(m),比赛时间是x(s),整个过程中y与x之间的函数关系的图象大致是( )
A. B.
C. D.
【分析】先算出甲到达终点的时间,由此算出二者之间的最大距离,再算出乙到达终点的时间,由此找出点的坐标,结合点的坐标利用待定系数法求出函数解析式,根据函数解析式分析四个选项即可得出结论.
解:当甲跑到终点时所用的时间为:2000÷8=250(秒),
此时甲乙间的距离为:2000﹣200﹣6×250=300(米),
乙到达终点时所用的时间为:(2000﹣200)÷6=300(秒),
∴最高点坐标为(250,300).
当0≤x≤100时,设y关于x的函数解析式为y=k1x+b1,
有,
解得:,
此时y=﹣2x+200;
当100<x≤250时,设y关于x的函数解析式为y=k2x+b2,
有,
解得:,
此时y=2x﹣200;
当250<x≤300时,设y关于x的函数解析式为y=k3x+b3,
有,
解得:,
此时y=﹣6x+1800.
∴整个过程中y与之间的函数图象是C.
故选:C.
二、填空题(每小题3分,共5小题,满分15分)
13.如图,在梯形ABCD中,AD∥BC,E、F分别为AB、DC上的点,若CF=4,且EF∥AD,AE:BE=2:3,则CD的长等于 .
【分析】由在梯形ABCD中,AD∥BC,EF∥AD,可得AD∥EF∥BC,然后由平行线分线段成比例定理,证得
,继而求得答案.
解:∵在梯形ABCD中,AD∥BC,EF∥AD,
∴AD∥EF∥BC,
∴==,
∴
∵CF=4,
∴DC=4=.
故答案为:.
14.已知关于x的一元二次方程(k+1)x2+2x﹣1=0有实数根,则k的取值范围是 k≥﹣2且k≠﹣1 .
【分析】利用一元二次方程的定义和根的判别式的意义得到k+1≠0且Δ=22﹣4×(k+1)×(﹣1)≥0,然后求出两个不等式的公共部分即可.
解:根据题意得k+1≠0且Δ=22﹣4×(k+1)×(﹣1)≥0,
解得k≥﹣2且k≠﹣1.
故答案为:k≥﹣2且k≠﹣1.
15.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 6π .
【分析】根据阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积,即可求解.
解:阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积=扇形ABB′的面积,
则阴影部分的面积是:=6π,
故答案为:6π.
16.如图,平行四边形ABCD中,AE:EB=2:3,DE交AC于F,△CDF的面积为20cm2,则△AEF的面积为 cm2.
【分析】由DC∥AB可知,△AEF∽△CDF,再运用相似三角形的性质:面积之比等于相似比的平方即可解决问题.
解:∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∴△AEF∽△CDF.
∵AE:EB=2:3,
设AE=2a,则BE=3a,DC=5a;
∵△AEF∽△CDF,
∴=()2,而==,
∵△CDF的面积为20cm2,
∴△AEF的面积为cm2.
故答案为:.
17.如图,直线l:y=﹣x,点A1坐标为(﹣3,0).经过A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2021的坐标为 (﹣,0) .
【分析】先根据一次函数解析式求出B1点的坐标,再根据B1点的坐标求出OA2的长,用同样的方法得出OA3,OA4的长,以此类推,总结规律便可求出点A2021的坐标.
解:∵点A1坐标为(﹣3,0),
∴OA1=3,
在y=﹣x中,当x=﹣3时,y=4,即B1点的坐标为(﹣3,4),
∴由勾股定理可得OB1==5,即OA2=5=3×,
同理可得,
OB2=,即OA3==5×()1,
OB3=,即OA4==5×()2,
以此类推,
OAn=5×()n﹣2=,
即点An坐标为(﹣,0),
当n=2021时,点A2021坐标为(﹣,0).
故答案为:(﹣,0).
三、解答题(共8小题,满分69分)
18.(1)解方程3x2+2x﹣2=0;
(2)解方程3x(x﹣1)=x﹣1;
(3)计算2cos60°+4sin60° tan30°﹣6cos245°.
【分析】(1)利用公式法求解即可;
(2)先移项,再将左边利用提公因式法因式分解,继而可得两个关于x的一元一次方程,分别求解即可得出答案;
(3)代入三角函数值,再计算乘法和乘方,继而计算加减即可.
解:(1)∵a=3,b=2,c=﹣2,
∴Δ=22﹣4×3×(﹣2)=28>0,
则x===,
∴x1=,x2=;
(2)∵3x(x﹣1)=x﹣1,
∴3x(x﹣1)﹣(x﹣1)=0,
则(x﹣1)(3x﹣1)=0,
∴x﹣1=0或3x﹣1=0,
解得x1=1,x2=;
(3)原式=2×+4××﹣6×()2
=1+2﹣6×
=1+2﹣3
=0.
19.如图,某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?
【分析】设矩形温室的宽为xm,则长为2xm,根据矩形的面积计算公式即可列出方程求解.
解:设矩形温室的宽为xm,则长为2xm,
根据题意,得(x﹣2) (2x﹣4)=288,
解得:x1=﹣10(不合题意,舍去),x2=14,
所以x=14,2x=2×14=28.
答:当矩形温室的长为28m,宽为14m时,蔬菜种植区域的面积是288m2.
20.如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的相似比为1:2,画出△A1B1C1,并标出△A1B1C1外接圆的圆心P,直接写出P点的坐标.
(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1,B1,C1)
(2)作出△ABC绕点C逆时针旋转90°后的图形△A2B2C,并求出点B经过的路径长.(结果保留根号和π)
【分析】(1)根据位似变换的定义得出三个顶点的对应点,再首尾顺次连接即可;
(2)将点A、B分别绕点C逆时针旋转90°后得到其对应点,再首尾顺次连接,继而利用弧长公式求解即可.
解:(1)如图,△A1B1C1和点P即为所求;点P的坐标为(3,1),
(2)如图,△A2B2C即为所求,
由题BC=,
点B的路径=.
21.如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
【分析】(1)根据矩形的性质和DF⊥AE,可得∠ABE=∠AFD=90°,∠AEB=∠DAF,即可证明△ABE∽△DFA.
(2)利用△ABE∽△ADF,得=,再利用勾股定理,求出AE的长,然后将已知数值代入即可求出DF的长.
解:(1)△ABE与△ADF相似.理由如下:
∵四边形ABCD为矩形,DF⊥AE,
∴∠ABE=∠AFD=90°,
∠AEB=∠DAF,
∴△ABE∽△DFA.
(2)∵△ABE∽△ADF
∴=,
∵在Rt△ABE中,AB=6,BE=8,
∴AE=10
∴DF===7.2.
答:DF的长为7.2.
22.农用温棚的上半部分如图所示,迎阳坡AD的坡度i=1:1.8,背阳坡AC坡度i=1:0.5,棚宽CD=11.5米,要铅直竖立两根立柱AB、EF,其中BF=AB.求AB、EF的长.
【分析】设AB=x米,根据坡度的概念用x表示出BD、BC,求出x,根据坡度的概念计算,得到答案.
解:设AB=x米,
∵迎阳坡AD的坡度i=1:1.8,
∴BD=1.8x米,
∵背阳坡AC坡度i=1:0.5,
∴CB=0.5x米,
∵CD=11.5米,
∴0.5x+1.8x=11.5,
解得:x=5,即AB=5米,
∵BF=AB,
∴BF=5米,
∴DF=4米,
∵迎阳坡AD的坡度i=1:1.8,
∴=,即=,
解得:EF=米.
综上所述:AB=5米,EF=米.
23.某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可售出240千克.
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系,每天销售200千克以上.
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式;
(2)该超市销售这种水果每天获取的利润达到1040元,那么销售单价为多少元?
【分析】(1)由于y是x的一次函数,则可利用待定系数法求解析式,设y=kx+b,把x=10,y=300;x=13,y=240代入即可得到y(千克)与x(元)(x>0)的函数关系式;
(2)根据每天获取的利润=每千克的利润×每天的销售量得到方程,然后解方程即可.
解:(1)设y=kx+b,
∵x=10,y=300;x=13,y=240,
∴,解得,
∴y=﹣20x+500;
(2)(x﹣8)(﹣20x+500)=1040,
整理,得x2﹣33x+252=0,
解得x1=12,x2=21.
当x=12时,销售量为﹣20×12+500=260>200,符合题意;
当x=21时,销售量为﹣20×21+500=80<200,不符合题意,舍去,
所以x=12.
即该超市销售这种水果每天获取的利润达到1040元,那么销售单价为12元.
24.如图,AE=AF,以AE为直径作⊙O交EF点D,过点D作BC⊥AF,交AE的延长线于点B.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=5,AC=4,求BE的长.
【分析】(1)连接OD,根据等腰三角形的性质得到∠OED=∠ODE,∠OED=∠F,求得∠ODE=∠F,根据平行线的判定得到OD∥AC,根据平行线的性质得到∠ODB=∠ACB,推出OD⊥BC,根据切线的判定定理即可得到结论;
(2)根据平行线分线段成比例定理得到,于是得到结论.
解:(1)BC与⊙O相切,
理由:连接OD,
∵OE=OD,
∴∠OED=∠ODE,
∵AE=AF,
∴∠OED=∠F,
∴∠ODE=∠F,
∴OD∥AC,
∴∠ODB=∠ACB,
∵DC⊥AF,
∴∠ACB=90°,
∴∠ODB=90°,
∴OD⊥BC,
∵OD是⊙O的半径,
∴BC与⊙O相切;
(2)∵OD∥AC,
∴,
∵AE=5,AC=4,
即,
∴BE=.
25.已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动,速度为1cm/;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动时间为xs(0<x<2),解答下列问题:
(1)如图①,当x为何值时,△APQ与△ACB相似;
(2)如图②,连接PC,当x为何值时,PQ=PC;
(3)是否存在某时刻x,使线段PQ恰好把Rt△ACB面积平分?若存在,求出此时x的值;若不存在,说明理由.
【分析】(1)由题意知:BP=x,AQ=2x,则AP=5﹣x,当△APQ∽△ABC时,得,当△APQ∽△ACB时,得,分别代入计算即可;
(2)过点P作PM⊥AC于H,则AM=2x+2﹣x=x+2,由PM∥BC,得,代入计算即可;
(3)若存在,则此时S△AQP=3(cm2),过点P作PH⊥AC于H,由PH∥BC,得,表示出PH的长,从而列出方程.
【解答】解(1)在Rt△ABC中,AB==5,
由题意知:BP=x,AQ=2x,则AP=5﹣x,
∵△APQ与△ACB相似,
①当△APQ∽△ABC时,
∴,
∴,
解得:x=;
②当△APQ∽△ACB时,
∴,
∴,
解得:x=.
故当x=或秒时,△APQ与△ACB相似;
(2)如图,过点P作PM⊥AC于H,
∴∠AMP=90°,
∵AQ=2x,
∴CQ=4﹣2x,
∵PQ=PC PM⊥AC,
∴QM=CM=CQ=2﹣x,
∴AM=2x+2﹣x=x+2,
∵∠C=90°,
∴∠AMP=∠C,
∴PM∥BC,
∴,
∴,
解得;
(3)存在某时刻x,使线段PQ恰好把△ABC的面积平分,理由为:
假设存在某时刻x,使线段PQ恰好把△ABC的面积平分,
有S△AQP=S△ABC,
∵S△ABC=AC BC=6(cm2),
∴此时S△AQP=3(cm2),
过点P作PH⊥AC于H,
∵∠C=90°,
∴AC⊥BC,
∴PH∥BC,
∴,
∴,
∴PH=3﹣x,
∴△AQP的面积为×AQ×PH=×2x(3﹣x)=﹣x2+3x,
即﹣x2+3x=3,
化简得:x2﹣5x+5=0,
∵Δ=(﹣5)2﹣4×1×5=5,
∴x=,
∵0<x<2,
∴x=,
则存在x=,使线段PQ恰好把△ABC的面积平分.
一、选择题(每小题3分,共12小题,满分36分)
1.在△ABC中,∠C=90°,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
2.关于x的一元二次方程ax2﹣5x+a2+a=0的一个根是0,则a的值是( )
A.0 B.1 C.﹣1 D.0或﹣1
3.如图,点P在△ABC的边AC上,下列条件中不能判断△ABP∽△ACB的是( )
A.∠ABP=∠C B.∠APB=∠ABC C.= D.=
4.用配方法解一元二次方程x2﹣4x﹣5=0的过程中,配方正确的是( )
A.(x+2)2=1 B.(x﹣2)2=1 C.(x+2)2=9 D.(x﹣2)2=9
5.在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
6.某县为发展教育事业,加强了对教育经费的投入,2012年投入3000万元,预计2014年投入5000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )
A.3000x2=5000
B.3000(1+x)2=5000
C.3000(1+x%)2=5000
D.3000(1+x)+3000(1+x)2=5000
7.如图,四边形ABCD为⊙O的内接四边形,E是BC延长线上的一点,已知∠BOD=130°,则∠DCE的度数为( )
A.45° B.50° C.65° D.75°
8.在函数y=中,自变量x的取值范围是( )
A.x≥﹣2且x≠1 B.x≤2且x≠1 C.x≠1 D.x≤﹣2
9.⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )
A.4 B.6 C.6 D.8
10.小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为16米,坡面上的影长为8米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
A.12+2米 B.24米 C.8+4米 D.20米
11.下列叙述正确的有( )
①圆内接四边形对角相等;②圆的切线垂直于圆的半径;③正多边形中心角的度数等于这个正多边形一个外角的度数;④过圆外一点所画的圆的两条切线长相等;⑤边长为6的正三角形,其边心距为2.
A.1个 B.2个 C.3个 D.4个
12.甲、乙两名同学在一段2000m长的笔直公路上进行自行车比赛,开始时甲在起点,乙在甲的前方200m处,他们同时同向出发匀速前进,甲的速度是8m/s,乙的速度是6m/s,先到达终点者在终点处等待.设甲、乙两人之间的距离是y(m),比赛时间是x(s),整个过程中y与x之间的函数关系的图象大致是( )
A. B.
C. D.
二、填空题(每小题3分,共5小题,满分15分)
13.如图,在梯形ABCD中,AD∥BC,E、F分别为AB、DC上的点,若CF=4,且EF∥AD,AE:BE=2:3,则CD的长等于 .
14.已知关于x的一元二次方程(k+1)x2+2x﹣1=0有实数根,则k的取值范围是 .
15.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 .
16.如图,平行四边形ABCD中,AE:EB=2:3,DE交AC于F,△CDF的面积为20cm2,则△AEF的面积为 cm2.
17.如图,直线l:y=﹣x,点A1坐标为(﹣3,0).经过A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2021的坐标为 .
三、解答题(共8小题,满分69分)
18.(1)解方程3x2+2x﹣2=0;
(2)解方程3x(x﹣1)=x﹣1;
(3)计算2cos60°+4sin60° tan30°﹣6cos245°.
19.如图,某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?
20.如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的相似比为1:2,画出△A1B1C1,并标出△A1B1C1外接圆的圆心P,直接写出P点的坐标.
(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1,B1,C1)
(2)作出△ABC绕点C逆时针旋转90°后的图形△A2B2C,并求出点B经过的路径长.(结果保留根号和π)
21.如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
22.农用温棚的上半部分如图所示,迎阳坡AD的坡度i=1:1.8,背阳坡AC坡度i=1:0.5,棚宽CD=11.5米,要铅直竖立两根立柱AB、EF,其中BF=AB.求AB、EF的长.
23.某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可售出240千克.
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系,每天销售200千克以上.
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式;
(2)该超市销售这种水果每天获取的利润达到1040元,那么销售单价为多少元?
24.如图,AE=AF,以AE为直径作⊙O交EF点D,过点D作BC⊥AF,交AE的延长线于点B.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=5,AC=4,求BE的长.
25.已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动,速度为1cm/;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动时间为xs(0<x<2),解答下列问题:
(1)如图①,当x为何值时,△APQ与△ACB相似;
(2)如图②,连接PC,当x为何值时,PQ=PC;
(3)是否存在某时刻x,使线段PQ恰好把Rt△ACB面积平分?若存在,求出此时x的值;若不存在,说明理由.
参考答案
一、选择题(每小题3分,共12小题,满分36分)
1.在△ABC中,∠C=90°,BC=2,sinA=,则边AC的长是( )
A. B.3 C. D.
【分析】先根据BC=2,sinA=求出AB的长度,再利用勾股定理即可求解.
解:∵sinA==,BC=2,
∴AB=3.
∴AC===.
故选:A.
2.关于x的一元二次方程ax2﹣5x+a2+a=0的一个根是0,则a的值是( )
A.0 B.1 C.﹣1 D.0或﹣1
【分析】根据一元二次方程的解的定义得到a2+a=0,解得a1=0,a2=﹣1,然后根据一元二次方程的定义确定满足条件的a的值.
解:把x=0代入ax2﹣5x+a2+a=0得a2+a=0,解得a1=0,a2=﹣1,
而a≠0,
所以a=﹣1.
故选:C.
3.如图,点P在△ABC的边AC上,下列条件中不能判断△ABP∽△ACB的是( )
A.∠ABP=∠C B.∠APB=∠ABC C.= D.=
【分析】根据相似三角形的判定定理(①有两角分别相等的两三角形相似,②有两边的比相等,并且它们的夹角也相等的两三角形相似)逐个进行判断即可.
解:A、∵∠A=∠A,∠ABP=∠C,
∴△ABP∽△ACB,故本选项错误;
B、∵∠A=∠A,∠APB=∠ABC,
∴△ABP∽△ACB,故本选项错误;
C、∵∠A=∠A,=,
∴△ABP∽△ACB.
故故本选项错误.
D、正确.不能判定△ABP∽△ACB.
故选:D.
4.用配方法解一元二次方程x2﹣4x﹣5=0的过程中,配方正确的是( )
A.(x+2)2=1 B.(x﹣2)2=1 C.(x+2)2=9 D.(x﹣2)2=9
【分析】先移项,再方程两边都加上一次项系数一半的平方,即可得出答案.
解:移项得:x2﹣4x=5,
配方得:x2﹣4x+22=5+22,
(x﹣2)2=9,
故选:D.
5.在平面直角坐标系xOy中,以点(﹣3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
【分析】首先画出图形,根据点的坐标得到圆心到X轴的距离是4,到Y轴的距离是3,根据直线与圆的位置关系即可求出答案.
解:圆心到X轴的距离是4,到y轴的距离是3,
4=4,3<4,
∴圆与x轴相切,与y轴相交,
故选:C.
6.某县为发展教育事业,加强了对教育经费的投入,2012年投入3000万元,预计2014年投入5000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )
A.3000x2=5000
B.3000(1+x)2=5000
C.3000(1+x%)2=5000
D.3000(1+x)+3000(1+x)2=5000
【分析】增长率问题,一般用增长后的量=增长前的量×(1+增长率),参照本题,如果设教育经费的年平均增长率为x,根据“2012年投入3000万元,预计2014年投入5000万元”,可以分别用x表示2012以后两年的投入,然后根据已知条件可得出方程.
解:设教育经费的年平均增长率为x,
则2013的教育经费为:3000×(1+x)万元,
2014的教育经费为:3000×(1+x)2万元,
那么可得方程:3000×(1+x)2=5000.
故选:B.
7.如图,四边形ABCD为⊙O的内接四边形,E是BC延长线上的一点,已知∠BOD=130°,则∠DCE的度数为( )
A.45° B.50° C.65° D.75°
【分析】根据圆周角定理求出∠A,根据圆内接四边形的性质得出∠DCE=∠A,代入求出即可.
解:∵∠BOD=130°,
∴∠A=∠BOD=65°,
∵四边形ABCD为⊙O的内接四边形,
∴∠DCE=∠A=65°,
故选:C.
8.在函数y=中,自变量x的取值范围是( )
A.x≥﹣2且x≠1 B.x≤2且x≠1 C.x≠1 D.x≤﹣2
【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.
解:由题意得,x+2≥0且x﹣1≠0,
解得x≥﹣2且x≠1.
故选:A.
9.⊙O的半径为5,M是圆外一点,MO=6,∠OMA=30°,则弦AB的长为( )
A.4 B.6 C.6 D.8
【分析】过O作OC⊥AB于C,连接OA,根据含30°角的直角三角形的性质得出OC=MO=3,根据勾股定理求出AC,再根据垂径定理得出AB=2AC,最后求出答案即可.
解:过O作OC⊥AB于C,连接OA,则∠OCA=90°,
∵MO=6,∠OMA=30°,
∴OC=MO=3,
在Rt△OCA中,由勾股定理得:AC===4,
∵OC⊥AB,OC过O,
∴BC=AC,
即AB=2AC=2×4=8,
故选:D.
10.小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为16米,坡面上的影长为8米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
A.12+2米 B.24米 C.8+4米 D.20米
【分析】延长AC交BF延长线于D点,则BD即为AB的影长,然后根据物长和影长的比值计算即可.
解:延长AC交BF延长线于D点,
则∠CFE=30°,作CE⊥BD于E,
在Rt△CFE中,∠CFE=30°,CF=8m,
∴CE=4(米),EF=8cos30°=4(米),
在Rt△CED中,
∵同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,CE=4(米),CE:DE=1:2,
∴DE=8(米),
∴BD=BF+EF+ED=16+4+8=24+4(米)
在Rt△ABD中,AB=BD=(24+4)=(12+2)(米),
故选:A.
11.下列叙述正确的有( )
①圆内接四边形对角相等;②圆的切线垂直于圆的半径;③正多边形中心角的度数等于这个正多边形一个外角的度数;④过圆外一点所画的圆的两条切线长相等;⑤边长为6的正三角形,其边心距为2.
A.1个 B.2个 C.3个 D.4个
【分析】利用圆内接四边形的性质、圆周角定理分别判断后即可确定正确的选项个数.
解:①圆内接四边形对角互补,故①不符合题意;
②圆的切线垂直于过切点的半径,故②不符合题意;
③正n多边形中心角的度数等于,这个正多边形的外角和为360°,一个外角的度数等于,故③符合题意;
④过圆外一点所画的圆的两条切线长相等,正确,故④符合题意;
⑤如图,△ABC为正三角形,点O为其中心;
OD⊥BC于点D;连接OB、OC;
∵OA=OC,∠BOC=×360°=120°,
∴BD=BC=3,∠BOD=120°=60°,
∴tan∠BOD=,
∴OD=×6×=,
即边长为6的正三角形的边心距为,故⑤不符合题意,
故选:B.
12.甲、乙两名同学在一段2000m长的笔直公路上进行自行车比赛,开始时甲在起点,乙在甲的前方200m处,他们同时同向出发匀速前进,甲的速度是8m/s,乙的速度是6m/s,先到达终点者在终点处等待.设甲、乙两人之间的距离是y(m),比赛时间是x(s),整个过程中y与x之间的函数关系的图象大致是( )
A. B.
C. D.
【分析】先算出甲到达终点的时间,由此算出二者之间的最大距离,再算出乙到达终点的时间,由此找出点的坐标,结合点的坐标利用待定系数法求出函数解析式,根据函数解析式分析四个选项即可得出结论.
解:当甲跑到终点时所用的时间为:2000÷8=250(秒),
此时甲乙间的距离为:2000﹣200﹣6×250=300(米),
乙到达终点时所用的时间为:(2000﹣200)÷6=300(秒),
∴最高点坐标为(250,300).
当0≤x≤100时,设y关于x的函数解析式为y=k1x+b1,
有,
解得:,
此时y=﹣2x+200;
当100<x≤250时,设y关于x的函数解析式为y=k2x+b2,
有,
解得:,
此时y=2x﹣200;
当250<x≤300时,设y关于x的函数解析式为y=k3x+b3,
有,
解得:,
此时y=﹣6x+1800.
∴整个过程中y与之间的函数图象是C.
故选:C.
二、填空题(每小题3分,共5小题,满分15分)
13.如图,在梯形ABCD中,AD∥BC,E、F分别为AB、DC上的点,若CF=4,且EF∥AD,AE:BE=2:3,则CD的长等于 .
【分析】由在梯形ABCD中,AD∥BC,EF∥AD,可得AD∥EF∥BC,然后由平行线分线段成比例定理,证得
,继而求得答案.
解:∵在梯形ABCD中,AD∥BC,EF∥AD,
∴AD∥EF∥BC,
∴==,
∴
∵CF=4,
∴DC=4=.
故答案为:.
14.已知关于x的一元二次方程(k+1)x2+2x﹣1=0有实数根,则k的取值范围是 k≥﹣2且k≠﹣1 .
【分析】利用一元二次方程的定义和根的判别式的意义得到k+1≠0且Δ=22﹣4×(k+1)×(﹣1)≥0,然后求出两个不等式的公共部分即可.
解:根据题意得k+1≠0且Δ=22﹣4×(k+1)×(﹣1)≥0,
解得k≥﹣2且k≠﹣1.
故答案为:k≥﹣2且k≠﹣1.
15.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是 6π .
【分析】根据阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积,即可求解.
解:阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积﹣以AB为直径的半圆的面积=扇形ABB′的面积,
则阴影部分的面积是:=6π,
故答案为:6π.
16.如图,平行四边形ABCD中,AE:EB=2:3,DE交AC于F,△CDF的面积为20cm2,则△AEF的面积为 cm2.
【分析】由DC∥AB可知,△AEF∽△CDF,再运用相似三角形的性质:面积之比等于相似比的平方即可解决问题.
解:∵四边形ABCD是平行四边形,
∴DC∥AB,DC=AB,
∴△AEF∽△CDF.
∵AE:EB=2:3,
设AE=2a,则BE=3a,DC=5a;
∵△AEF∽△CDF,
∴=()2,而==,
∵△CDF的面积为20cm2,
∴△AEF的面积为cm2.
故答案为:.
17.如图,直线l:y=﹣x,点A1坐标为(﹣3,0).经过A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2021的坐标为 (﹣,0) .
【分析】先根据一次函数解析式求出B1点的坐标,再根据B1点的坐标求出OA2的长,用同样的方法得出OA3,OA4的长,以此类推,总结规律便可求出点A2021的坐标.
解:∵点A1坐标为(﹣3,0),
∴OA1=3,
在y=﹣x中,当x=﹣3时,y=4,即B1点的坐标为(﹣3,4),
∴由勾股定理可得OB1==5,即OA2=5=3×,
同理可得,
OB2=,即OA3==5×()1,
OB3=,即OA4==5×()2,
以此类推,
OAn=5×()n﹣2=,
即点An坐标为(﹣,0),
当n=2021时,点A2021坐标为(﹣,0).
故答案为:(﹣,0).
三、解答题(共8小题,满分69分)
18.(1)解方程3x2+2x﹣2=0;
(2)解方程3x(x﹣1)=x﹣1;
(3)计算2cos60°+4sin60° tan30°﹣6cos245°.
【分析】(1)利用公式法求解即可;
(2)先移项,再将左边利用提公因式法因式分解,继而可得两个关于x的一元一次方程,分别求解即可得出答案;
(3)代入三角函数值,再计算乘法和乘方,继而计算加减即可.
解:(1)∵a=3,b=2,c=﹣2,
∴Δ=22﹣4×3×(﹣2)=28>0,
则x===,
∴x1=,x2=;
(2)∵3x(x﹣1)=x﹣1,
∴3x(x﹣1)﹣(x﹣1)=0,
则(x﹣1)(3x﹣1)=0,
∴x﹣1=0或3x﹣1=0,
解得x1=1,x2=;
(3)原式=2×+4××﹣6×()2
=1+2﹣6×
=1+2﹣3
=0.
19.如图,某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?
【分析】设矩形温室的宽为xm,则长为2xm,根据矩形的面积计算公式即可列出方程求解.
解:设矩形温室的宽为xm,则长为2xm,
根据题意,得(x﹣2) (2x﹣4)=288,
解得:x1=﹣10(不合题意,舍去),x2=14,
所以x=14,2x=2×14=28.
答:当矩形温室的长为28m,宽为14m时,蔬菜种植区域的面积是288m2.
20.如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形,建立如图所示的平面直角坐标系,点C的坐标为(0,﹣1).
(1)在如图的方格纸中把△ABC以点O为位似中心扩大,使放大前后的相似比为1:2,画出△A1B1C1,并标出△A1B1C1外接圆的圆心P,直接写出P点的坐标.
(△ABC与△A1B1C1在位似中心O点的两侧,A,B,C的对应点分别是A1,B1,C1)
(2)作出△ABC绕点C逆时针旋转90°后的图形△A2B2C,并求出点B经过的路径长.(结果保留根号和π)
【分析】(1)根据位似变换的定义得出三个顶点的对应点,再首尾顺次连接即可;
(2)将点A、B分别绕点C逆时针旋转90°后得到其对应点,再首尾顺次连接,继而利用弧长公式求解即可.
解:(1)如图,△A1B1C1和点P即为所求;点P的坐标为(3,1),
(2)如图,△A2B2C即为所求,
由题BC=,
点B的路径=.
21.如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
【分析】(1)根据矩形的性质和DF⊥AE,可得∠ABE=∠AFD=90°,∠AEB=∠DAF,即可证明△ABE∽△DFA.
(2)利用△ABE∽△ADF,得=,再利用勾股定理,求出AE的长,然后将已知数值代入即可求出DF的长.
解:(1)△ABE与△ADF相似.理由如下:
∵四边形ABCD为矩形,DF⊥AE,
∴∠ABE=∠AFD=90°,
∠AEB=∠DAF,
∴△ABE∽△DFA.
(2)∵△ABE∽△ADF
∴=,
∵在Rt△ABE中,AB=6,BE=8,
∴AE=10
∴DF===7.2.
答:DF的长为7.2.
22.农用温棚的上半部分如图所示,迎阳坡AD的坡度i=1:1.8,背阳坡AC坡度i=1:0.5,棚宽CD=11.5米,要铅直竖立两根立柱AB、EF,其中BF=AB.求AB、EF的长.
【分析】设AB=x米,根据坡度的概念用x表示出BD、BC,求出x,根据坡度的概念计算,得到答案.
解:设AB=x米,
∵迎阳坡AD的坡度i=1:1.8,
∴BD=1.8x米,
∵背阳坡AC坡度i=1:0.5,
∴CB=0.5x米,
∵CD=11.5米,
∴0.5x+1.8x=11.5,
解得:x=5,即AB=5米,
∵BF=AB,
∴BF=5米,
∴DF=4米,
∵迎阳坡AD的坡度i=1:1.8,
∴=,即=,
解得:EF=米.
综上所述:AB=5米,EF=米.
23.某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可售出240千克.
小红:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系,每天销售200千克以上.
(1)求每天的销售量y(千克)与销售单价x(元)之间的函数关系式;
(2)该超市销售这种水果每天获取的利润达到1040元,那么销售单价为多少元?
【分析】(1)由于y是x的一次函数,则可利用待定系数法求解析式,设y=kx+b,把x=10,y=300;x=13,y=240代入即可得到y(千克)与x(元)(x>0)的函数关系式;
(2)根据每天获取的利润=每千克的利润×每天的销售量得到方程,然后解方程即可.
解:(1)设y=kx+b,
∵x=10,y=300;x=13,y=240,
∴,解得,
∴y=﹣20x+500;
(2)(x﹣8)(﹣20x+500)=1040,
整理,得x2﹣33x+252=0,
解得x1=12,x2=21.
当x=12时,销售量为﹣20×12+500=260>200,符合题意;
当x=21时,销售量为﹣20×21+500=80<200,不符合题意,舍去,
所以x=12.
即该超市销售这种水果每天获取的利润达到1040元,那么销售单价为12元.
24.如图,AE=AF,以AE为直径作⊙O交EF点D,过点D作BC⊥AF,交AE的延长线于点B.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=5,AC=4,求BE的长.
【分析】(1)连接OD,根据等腰三角形的性质得到∠OED=∠ODE,∠OED=∠F,求得∠ODE=∠F,根据平行线的判定得到OD∥AC,根据平行线的性质得到∠ODB=∠ACB,推出OD⊥BC,根据切线的判定定理即可得到结论;
(2)根据平行线分线段成比例定理得到,于是得到结论.
解:(1)BC与⊙O相切,
理由:连接OD,
∵OE=OD,
∴∠OED=∠ODE,
∵AE=AF,
∴∠OED=∠F,
∴∠ODE=∠F,
∴OD∥AC,
∴∠ODB=∠ACB,
∵DC⊥AF,
∴∠ACB=90°,
∴∠ODB=90°,
∴OD⊥BC,
∵OD是⊙O的半径,
∴BC与⊙O相切;
(2)∵OD∥AC,
∴,
∵AE=5,AC=4,
即,
∴BE=.
25.已知:如图,在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm.点P由B出发沿BA方向向点A匀速运动,速度为1cm/;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动时间为xs(0<x<2),解答下列问题:
(1)如图①,当x为何值时,△APQ与△ACB相似;
(2)如图②,连接PC,当x为何值时,PQ=PC;
(3)是否存在某时刻x,使线段PQ恰好把Rt△ACB面积平分?若存在,求出此时x的值;若不存在,说明理由.
【分析】(1)由题意知:BP=x,AQ=2x,则AP=5﹣x,当△APQ∽△ABC时,得,当△APQ∽△ACB时,得,分别代入计算即可;
(2)过点P作PM⊥AC于H,则AM=2x+2﹣x=x+2,由PM∥BC,得,代入计算即可;
(3)若存在,则此时S△AQP=3(cm2),过点P作PH⊥AC于H,由PH∥BC,得,表示出PH的长,从而列出方程.
【解答】解(1)在Rt△ABC中,AB==5,
由题意知:BP=x,AQ=2x,则AP=5﹣x,
∵△APQ与△ACB相似,
①当△APQ∽△ABC时,
∴,
∴,
解得:x=;
②当△APQ∽△ACB时,
∴,
∴,
解得:x=.
故当x=或秒时,△APQ与△ACB相似;
(2)如图,过点P作PM⊥AC于H,
∴∠AMP=90°,
∵AQ=2x,
∴CQ=4﹣2x,
∵PQ=PC PM⊥AC,
∴QM=CM=CQ=2﹣x,
∴AM=2x+2﹣x=x+2,
∵∠C=90°,
∴∠AMP=∠C,
∴PM∥BC,
∴,
∴,
解得;
(3)存在某时刻x,使线段PQ恰好把△ABC的面积平分,理由为:
假设存在某时刻x,使线段PQ恰好把△ABC的面积平分,
有S△AQP=S△ABC,
∵S△ABC=AC BC=6(cm2),
∴此时S△AQP=3(cm2),
过点P作PH⊥AC于H,
∵∠C=90°,
∴AC⊥BC,
∴PH∥BC,
∴,
∴,
∴PH=3﹣x,
∴△AQP的面积为×AQ×PH=×2x(3﹣x)=﹣x2+3x,
即﹣x2+3x=3,
化简得:x2﹣5x+5=0,
∵Δ=(﹣5)2﹣4×1×5=5,
∴x=,
∵0<x<2,
∴x=,
则存在x=,使线段PQ恰好把△ABC的面积平分.
同课章节目录
