沪科版数学九年级上册 22.3 相似三角形的性质(课件)(共14张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 22.3 相似三角形的性质(课件)(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 161.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
22.3 相似三角形的性质
回顾旧知
1.相似三角形的定义:
对应角相等,对应边成比例的两个三角形,是相似三角形。
①“A”型、“X”型 ②两角
③两边及夹角 ④三边⑤一直角边和斜边
2.相似三角形的判定方法:
3.已经学习的相似三角形的性质:
对应角相等,对应边成比例
问题1
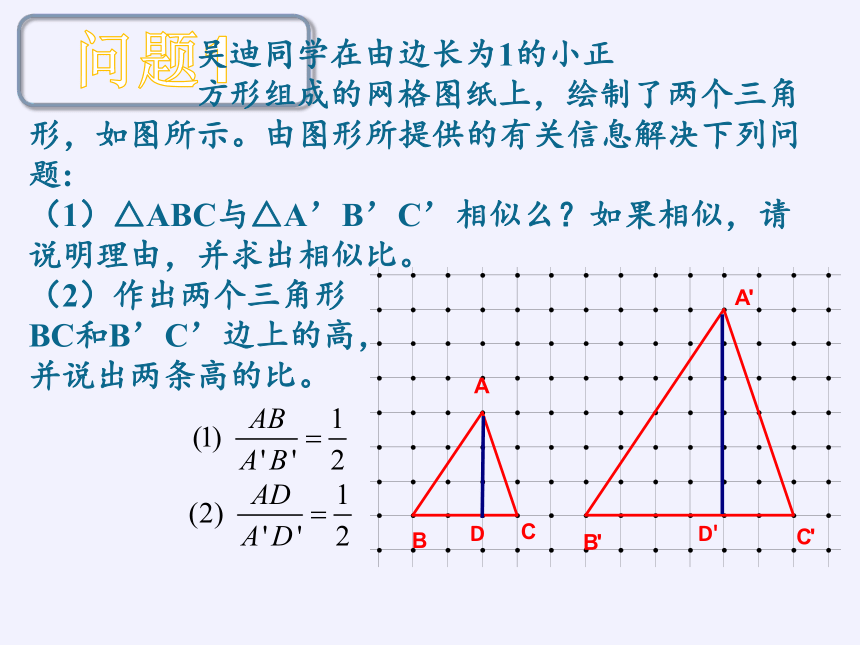
吴迪同学在由边长为1的小正
方形组成的网格图纸上,绘制了两个三角形,如图所示。由图形所提供的有关信息解决下列问题:
(1)△ABC与△A’B’C’相似么?如果相似,请说明理由,并求出相似比。
(2)作出两个三角形
BC和B’C’边上的高,
并说出两条高的比。
D
D'
问题2-1
猜想
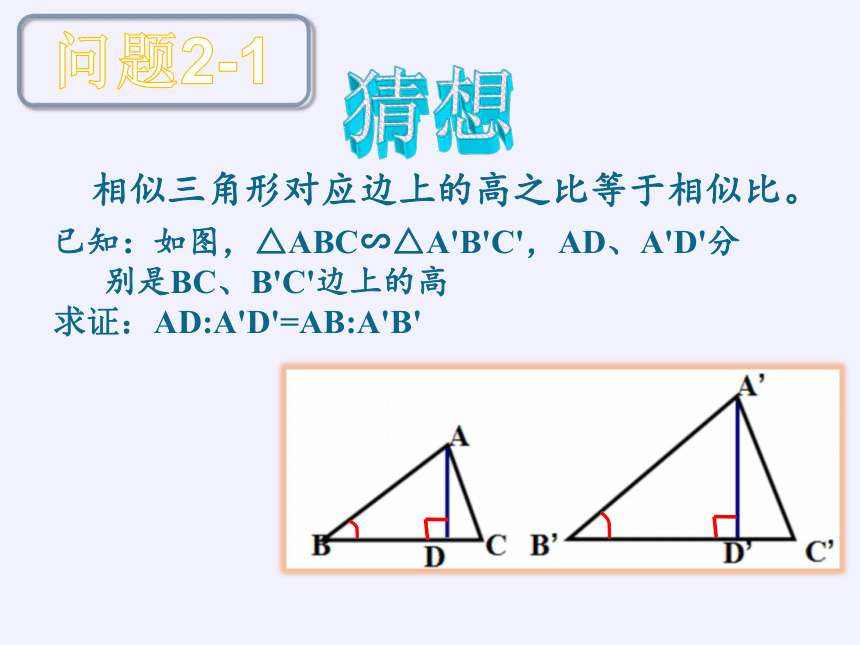
相似三角形对应边上的高之比等于相似比。
已知:如图,△ABC∽△A'B'C',AD、A'D'分
别是BC、B'C'边上的高
求证:AD:A'D'=AB:A'B'
问题2-2
猜想
相似三角形对应边上的高之比等于相似比。
相似三角形对应边上的中线之比等于相似比。
相似三角形对应角的角平分线之比等于相似比。
问题2-2
猜想
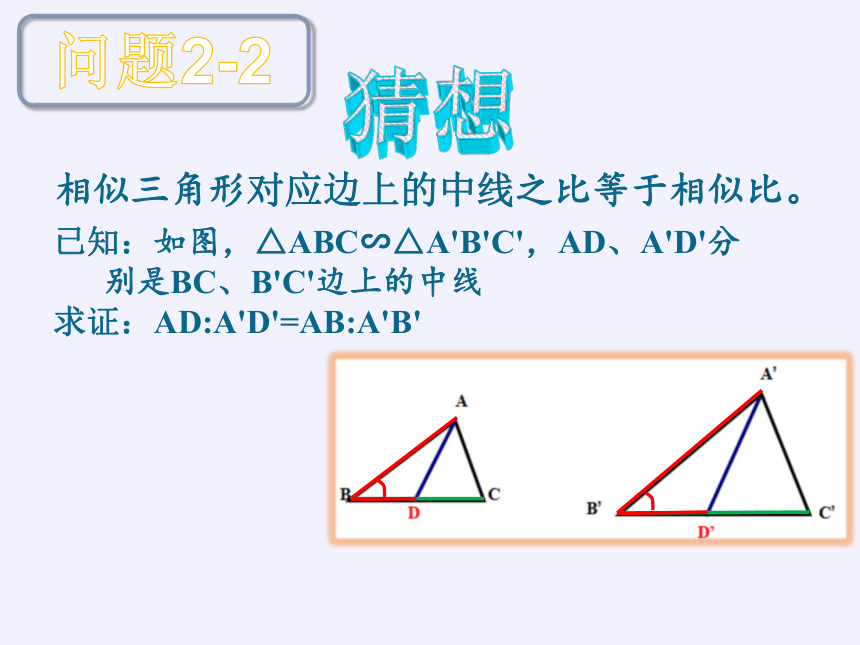
相似三角形对应边上的中线之比等于相似比。
已知:如图,△ABC∽△A'B'C',AD、A'D'分
别是BC、B'C'边上的中线
求证:AD:A'D'=AB:A'B'
问题2-2
定理1
相似三角形的对应高之比、对应中线之
比、对应角平分线之比都等于相似比。
问题3
已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
M
N
典型例题
如图, △ABC是一块锐角三角形的余料,边长BC=60cm,高AD=40cm,要把它加工成正方形零件,使正方形的一边FG在BC上,其余两个顶点E、H分别在AB、AC上,高AD与EH相交于点P.
(1)△AEH与△ABC相似么?为什么?
(2)求这个正方形的零件的边长.
变式1
已知:如图,FGHI为矩形,AD⊥BC于D,FG:GH=1:2,BC=30cm,AD=12cm 。
求:矩形FGNI的面积。
变式2
如图,矩形FGHN内接于△ABC,FG在BC上,NH分别在AB、AC上,且AD⊥BC于D,交NH于E,AD=8cm,BC=24cm。
(1)设NF=xcm,用含有x的式子表示NH的长;
(2)求矩形FGHN的面积的最大值。
课堂小结
对应角相等、对应边成比例
对应高之比、对应中线之比、对应角平分线之比
等于相似比
对应周长之比等于相似比
对应面积之比等于相似比的平方
作业布置
课本第90-91页
练习1、2
习题2、3、10
认真
端正
谢 谢
22.3 相似三角形的性质
回顾旧知
1.相似三角形的定义:
对应角相等,对应边成比例的两个三角形,是相似三角形。
①“A”型、“X”型 ②两角
③两边及夹角 ④三边⑤一直角边和斜边
2.相似三角形的判定方法:
3.已经学习的相似三角形的性质:
对应角相等,对应边成比例
问题1
吴迪同学在由边长为1的小正
方形组成的网格图纸上,绘制了两个三角形,如图所示。由图形所提供的有关信息解决下列问题:
(1)△ABC与△A’B’C’相似么?如果相似,请说明理由,并求出相似比。
(2)作出两个三角形
BC和B’C’边上的高,
并说出两条高的比。
D
D'
问题2-1
猜想
相似三角形对应边上的高之比等于相似比。
已知:如图,△ABC∽△A'B'C',AD、A'D'分
别是BC、B'C'边上的高
求证:AD:A'D'=AB:A'B'
问题2-2
猜想
相似三角形对应边上的高之比等于相似比。
相似三角形对应边上的中线之比等于相似比。
相似三角形对应角的角平分线之比等于相似比。
问题2-2
猜想
相似三角形对应边上的中线之比等于相似比。
已知:如图,△ABC∽△A'B'C',AD、A'D'分
别是BC、B'C'边上的中线
求证:AD:A'D'=AB:A'B'
问题2-2
定理1
相似三角形的对应高之比、对应中线之
比、对应角平分线之比都等于相似比。
问题3
已知△ABC∽△DEF,BG、EH分△ABC和△DEF的角平分线,BC=6cm,EF=4cm,BG=4.8cm.求EH的长.
M
N
典型例题
如图, △ABC是一块锐角三角形的余料,边长BC=60cm,高AD=40cm,要把它加工成正方形零件,使正方形的一边FG在BC上,其余两个顶点E、H分别在AB、AC上,高AD与EH相交于点P.
(1)△AEH与△ABC相似么?为什么?
(2)求这个正方形的零件的边长.
变式1
已知:如图,FGHI为矩形,AD⊥BC于D,FG:GH=1:2,BC=30cm,AD=12cm 。
求:矩形FGNI的面积。
变式2
如图,矩形FGHN内接于△ABC,FG在BC上,NH分别在AB、AC上,且AD⊥BC于D,交NH于E,AD=8cm,BC=24cm。
(1)设NF=xcm,用含有x的式子表示NH的长;
(2)求矩形FGHN的面积的最大值。
课堂小结
对应角相等、对应边成比例
对应高之比、对应中线之比、对应角平分线之比
等于相似比
对应周长之比等于相似比
对应面积之比等于相似比的平方
作业布置
课本第90-91页
练习1、2
习题2、3、10
认真
端正
谢 谢
