沪科版数学九年级上册 23.2 解直角三角形 教案
文档属性
| 名称 | 沪科版数学九年级上册 23.2 解直角三角形 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 57.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 00:00:00 | ||
图片预览

文档简介
三角形面积公式及其应用
教学目标:
理解三角形面积公式,会运用三角形面积公式解决实际问题;
通过对三角形面积公式的运用,逐步培养学生分析问题、解决问题的能力。
教学重点:
熟记三角形面积公式及正弦定理
教学难点:
三角形面积公式的灵活运用
教学准备:班班通
教学过程:
一、复习引导
(
A
B
C
a
b
c
S
△
ABC=1/2
底
*
高
) 师:以前我们学习过三角形面积公式,你还记得吗?
既然是底与高乘积的一半,三角形有三条边,那应该哪条边作为底呢?
看图,应该有三种情况:S= aha= bhb= chc
引入:除了用上述公式求三角形面积,还有其他公式求三角形的面积吗?今天我们就来学习三角形面积公式的推导及应用。
二、授新
(
D
A
B
C
a
b=4
c=6
60
°
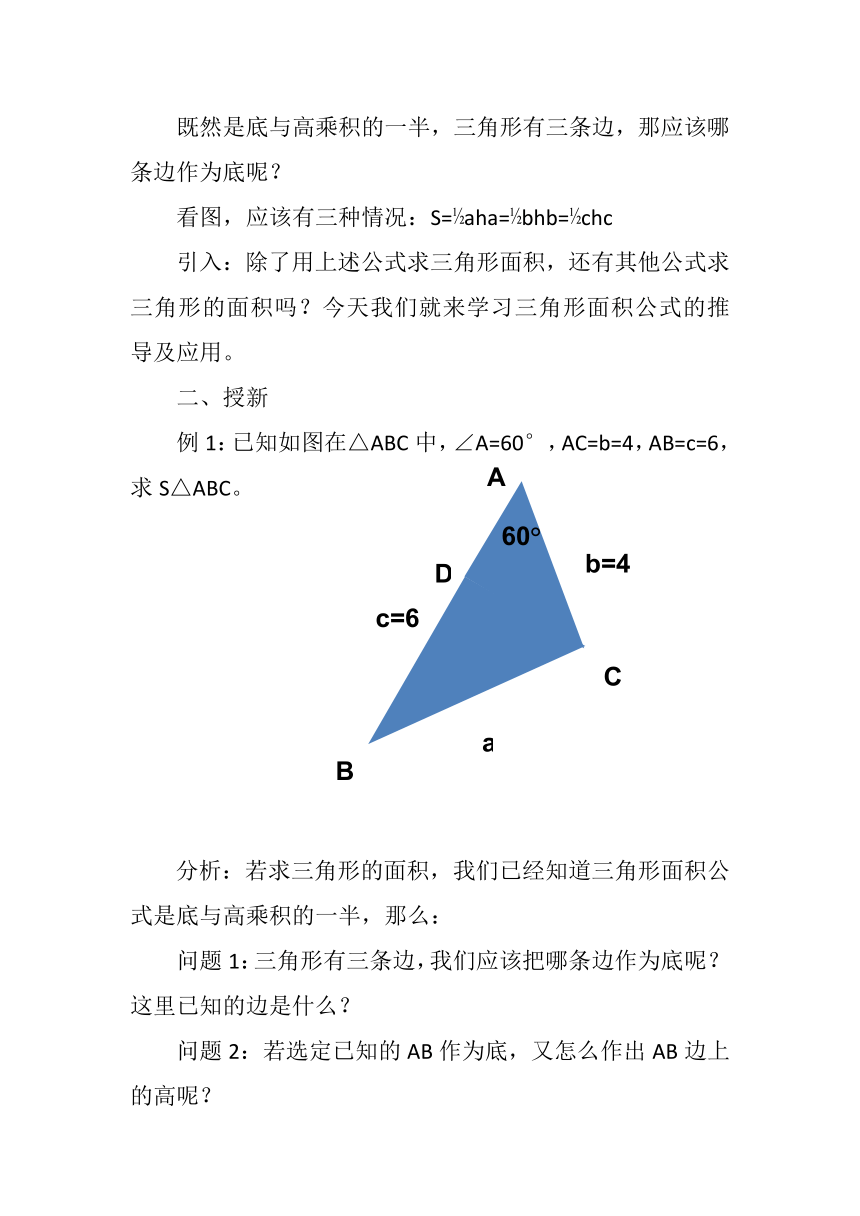
) 例1:已知如图在△ABC中,∠A=60°,AC=b=4,AB=c=6,求S△ABC。
分析:若求三角形的面积,我们已经知道三角形面积公式是底与高乘积的一半,那么:
问题1:三角形有三条边,我们应该把哪条边作为底呢?这里已知的边是什么?
问题2:若选定已知的AB作为底,又怎么作出AB边上的高呢?
问题3:又怎样求出所作的高呢?这里有2个直角三角形,根据现有条件,通过解哪个直角三角形求CD呢?
解:过点C作CD⊥AB于点D,△ACD中∠ADC=90°,sinA=CD/AC
∴CD=AC*sinA=b*sinA
∴S△ABC=1/2AB*CD=1/2AB*AC*sinA=1/2c*b*sinA,
当∠A=60°,b=4,c=6时,有:
S△ABC=1/2c*b*sinA=1/2*4*6*sin60°=6√3
点评:此例得出S△ABC=1/2c*b*sinA,即△ABC的面积公式。
b、c、A分别是什么?
猜想:△ABC的面积是否可以用a、c以及夹角B的正弦或者a、b以及夹角A的正弦来表示?如果可以,怎么证明。
(
A
B
C
a
b
c
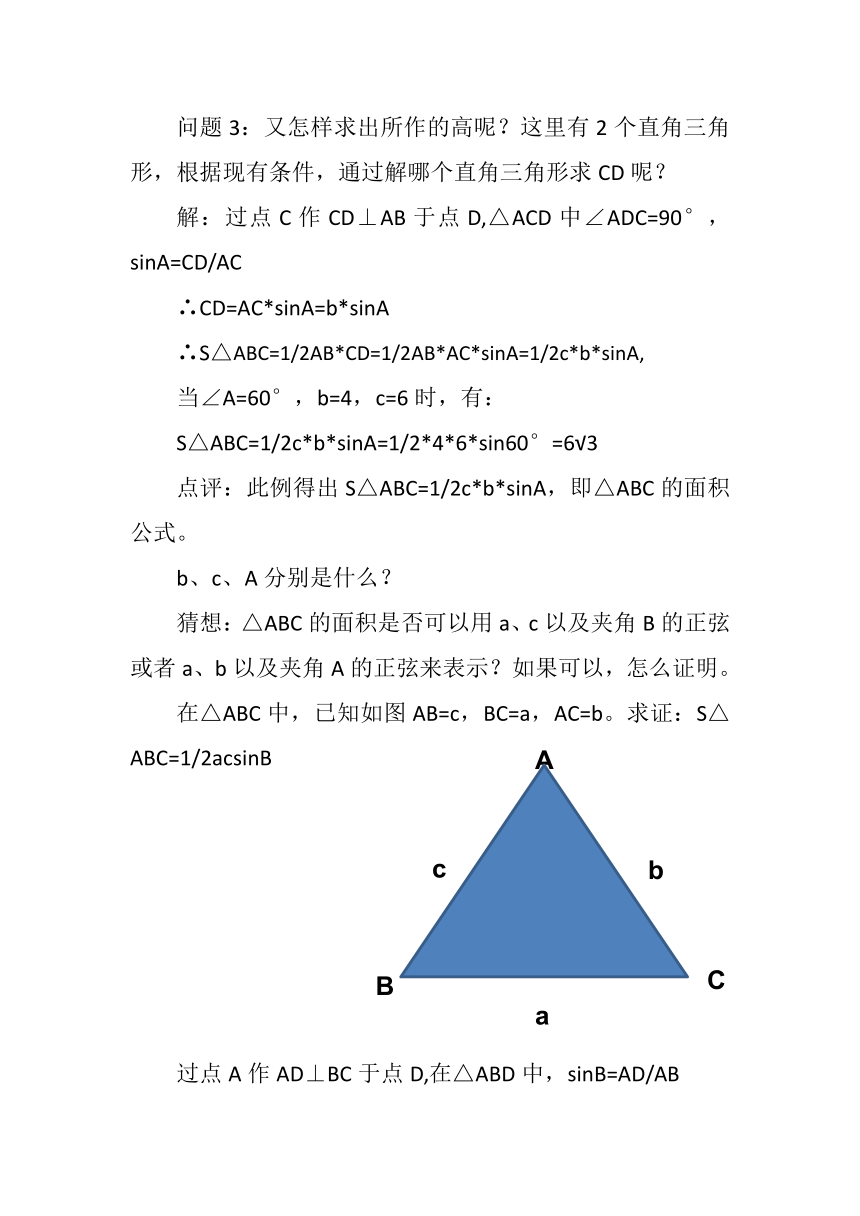
)在△ABC中,已知如图AB=c,BC=a,AC=b。求证:S△ABC=1/2acsinB
过点A作AD⊥BC于点D,在△ABD中,sinB=AD/AB
∴AD=AB*sinB=b*sinA
∴S△ABC=1/2BC*AD=1/2BC*AB*sinB=1/2a*c*sinB
同理可得S△ABC=1/2a*b*sinC
请记住:今天推导的三角形面积公式:S△ABC=1/2absinC=1/2acsinB=1/2bcsinA
此公式告诉我们:只要已知三角形的两边和这两边的夹角,就可以利用公式求出三角形的面积
除可求三角形面积外,还可解决三角形中边角关系
如果对刚才的公式适当变形:1/2bcsinA=1/2acsinB,即:a/sinA=b/sinB,同理,a/sinA=b/sinB
(
∴
)
此公式就叫做正弦定理!非常重要!非常重要!非常重要!
三、练习
已知:如图△ABC的三个顶点均在正方形网点上,求sinA的值。
(
A
B
C
a
b
c
)
解:由图可知,a=4,c=5,b=√17 sinB=4/5
∵a/sinA=b/sinB
∴sinA=16 √17/85
例2:已知:如图△ABC中,∠A=60°,
(
A
B
C
a=6
b
c
60
°
)BC=a=6,求△ABC的外接圆半径。
问题1:要求什么?如果能求出直径行否?圆中可作几条直径?
问题2:过点B作圆的直径BD,交圆于点D,能否把求直径BD转化为解直角三角形?有直角三角形吗?怎么办?
问题3:在△BCD中,已知什么?除BC=a=6,还有什么?如何利用三角函数求解?
解:过点B作圆的直径BD,交圆于点D,连接CD
∠D=∠A=60°,∠BCD=90°,sinD=BC/BD
∴BD=BC/sinD=a/sinD=a/sinA=2R
∴当a=6,∠A=60°时,6/sin60°=2R,R=2√3
(
=2R
(定值)
)通过此题,可以把正弦定理进一步完善
问题:这里R是什么?利用此定理可以解决与圆有关的知识吗?
巩固练习:
题1:已知:在△ABC中,AC=b=12,sinB=2/3,求△ABC的外接圆半径?
题2:已知△ABC的外接圆直径是10,BC=a=5√3,求BC所对的圆周角的度数?
小结
拓展训练
板书设计
三角形面积公式推导及应用
例1 三角形面积公式 例2 复习
正弦定理 练习
教学反思
教学目标:
理解三角形面积公式,会运用三角形面积公式解决实际问题;
通过对三角形面积公式的运用,逐步培养学生分析问题、解决问题的能力。
教学重点:
熟记三角形面积公式及正弦定理
教学难点:
三角形面积公式的灵活运用
教学准备:班班通
教学过程:
一、复习引导
(
A
B
C
a
b
c
S
△
ABC=1/2
底
*
高
) 师:以前我们学习过三角形面积公式,你还记得吗?
既然是底与高乘积的一半,三角形有三条边,那应该哪条边作为底呢?
看图,应该有三种情况:S= aha= bhb= chc
引入:除了用上述公式求三角形面积,还有其他公式求三角形的面积吗?今天我们就来学习三角形面积公式的推导及应用。
二、授新
(
D
A
B
C
a
b=4
c=6
60
°
) 例1:已知如图在△ABC中,∠A=60°,AC=b=4,AB=c=6,求S△ABC。
分析:若求三角形的面积,我们已经知道三角形面积公式是底与高乘积的一半,那么:
问题1:三角形有三条边,我们应该把哪条边作为底呢?这里已知的边是什么?
问题2:若选定已知的AB作为底,又怎么作出AB边上的高呢?
问题3:又怎样求出所作的高呢?这里有2个直角三角形,根据现有条件,通过解哪个直角三角形求CD呢?
解:过点C作CD⊥AB于点D,△ACD中∠ADC=90°,sinA=CD/AC
∴CD=AC*sinA=b*sinA
∴S△ABC=1/2AB*CD=1/2AB*AC*sinA=1/2c*b*sinA,
当∠A=60°,b=4,c=6时,有:
S△ABC=1/2c*b*sinA=1/2*4*6*sin60°=6√3
点评:此例得出S△ABC=1/2c*b*sinA,即△ABC的面积公式。
b、c、A分别是什么?
猜想:△ABC的面积是否可以用a、c以及夹角B的正弦或者a、b以及夹角A的正弦来表示?如果可以,怎么证明。
(
A
B
C
a
b
c
)在△ABC中,已知如图AB=c,BC=a,AC=b。求证:S△ABC=1/2acsinB
过点A作AD⊥BC于点D,在△ABD中,sinB=AD/AB
∴AD=AB*sinB=b*sinA
∴S△ABC=1/2BC*AD=1/2BC*AB*sinB=1/2a*c*sinB
同理可得S△ABC=1/2a*b*sinC
请记住:今天推导的三角形面积公式:S△ABC=1/2absinC=1/2acsinB=1/2bcsinA
此公式告诉我们:只要已知三角形的两边和这两边的夹角,就可以利用公式求出三角形的面积
除可求三角形面积外,还可解决三角形中边角关系
如果对刚才的公式适当变形:1/2bcsinA=1/2acsinB,即:a/sinA=b/sinB,同理,a/sinA=b/sinB
(
∴
)
此公式就叫做正弦定理!非常重要!非常重要!非常重要!
三、练习
已知:如图△ABC的三个顶点均在正方形网点上,求sinA的值。
(
A
B
C
a
b
c
)
解:由图可知,a=4,c=5,b=√17 sinB=4/5
∵a/sinA=b/sinB
∴sinA=16 √17/85
例2:已知:如图△ABC中,∠A=60°,
(
A
B
C
a=6
b
c
60
°
)BC=a=6,求△ABC的外接圆半径。
问题1:要求什么?如果能求出直径行否?圆中可作几条直径?
问题2:过点B作圆的直径BD,交圆于点D,能否把求直径BD转化为解直角三角形?有直角三角形吗?怎么办?
问题3:在△BCD中,已知什么?除BC=a=6,还有什么?如何利用三角函数求解?
解:过点B作圆的直径BD,交圆于点D,连接CD
∠D=∠A=60°,∠BCD=90°,sinD=BC/BD
∴BD=BC/sinD=a/sinD=a/sinA=2R
∴当a=6,∠A=60°时,6/sin60°=2R,R=2√3
(
=2R
(定值)
)通过此题,可以把正弦定理进一步完善
问题:这里R是什么?利用此定理可以解决与圆有关的知识吗?
巩固练习:
题1:已知:在△ABC中,AC=b=12,sinB=2/3,求△ABC的外接圆半径?
题2:已知△ABC的外接圆直径是10,BC=a=5√3,求BC所对的圆周角的度数?
小结
拓展训练
板书设计
三角形面积公式推导及应用
例1 三角形面积公式 例2 复习
正弦定理 练习
教学反思
